New solutions of Meyerhof's bearing capacity for foundations near slopes under asymmetric failure modes
-
摘要: 利用统一强度理论的平面应变强度方程，综合考虑中间主应力、基础至坡肩的水平距离、边坡高度和基底粗糙情况等因素，提出临坡地基坡面非对称破坏模式和坡底非对称破坏模式，继而建立条形基础下临坡地基新的Meyerhof承载力解答，给出具体应用步骤并开展理论退化分析与对比验证。研究表明：考虑坡后土体强度贡献所提出的非对称破坏模式更符合临坡地基的实际破坏形态；所得临坡地基Meyerhof承载力解答与文献模型试验和数值模拟均吻合良好；中间主应力可明显提高临坡地基的承载力；临坡地基承载力随边坡高度增加先减小后恒定。研究结果合理反映了土体强度的中间主应力效应、破坏模式的非对称性以及基础旁侧土体强度等工程实际情况，对临坡地基优化设计具有一定的理论指导意义。
-
关键词:
- 临坡地基 /
- 地基承载力 /
- 非对称破坏模式 /
- Meyerhof理论 /
- 统一强度理论
Abstract: The asymmetric failure modes involving the slope face failure and the below-toe failure are proposed, and then new solutions of Meyerhof's bearing capacity for strip foundations near slopes are presented by adopting the shear strength equation of unified strength theory under plane strain conditions. The combined effects of the intermediate principal stress, the horizontal distance of foundation from the slope shoulder, the slope height and the base roughness are taken into account. The specific application steps of the obtained solutions are provided, and theoretical degradation analysis and comparison verifications are conducted. It is found herein that the proposed asymmetrical failure mode considering the contribution of soil strength behind the slope is more consistent with the actual failure behavior of foundations near slopes. The obtained solutions of Meyerhof's bearing capacity for foundations near slopes are in good agreement with those of the model tests and numerical simulations in the literature. The intermediate principal stress has a marked improvement effect on the bearing capacity of foundations near slopes. The bearing capacity of foundations near slopes first decreases and then remains unchanged with the increase of the slope height. This study accounts for practical engineering conditions, such as the intermediate principal stress effect of soil strength, the asymmetry of failure modes and soil strength at foundation lateral side, which is of theoretical guiding significance to the optimal design of foundations near slopes. -
0. 引言
在交通、水利和建筑等工程建设中，基础常被布置于边坡或基坑附近，使得临坡地基的承载力有所减小。现有临坡地基承载力解答大多借助均布超载描述基础埋深内土体自重的贡献，不计基础旁侧的土体强度。Meyerhof理论通过“等代自由面”上的等代应力反映基础旁侧土体强度的影响，更符合地基的实际破坏形态[1]。胡卫东等[2]假定地基破坏时基础下三角形弹性区是对称的，基于Meyerhof理论推导了临坡地基承载力公式。然而，临坡基础下土体应力不均匀引起了地基破坏模式的非对称性，基础下弹性破坏区为非对称的三角形楔体[3]。另外，郑刚等[4]的数值模拟表明条形基础下临坡地基可能发生坡面、坡脚、坡底或水平对称等破坏模式，Chen等[5]获得了坡面破坏和坡底破坏下临坡地基的非对称破坏模式以及承载力上限法解答。
上述临坡地基承载力计算均采用Mohr-Coulomb强度准则，忽略了中间主应力对地基土体强度的提高作用，所得结果常偏于保守。统一强度理论合理解释了岩土类材料强度的中间主应力效应[6-7]，已广泛应用于水平地基承载力分析。因此，本文基于统一强度理论，考虑滑动区域内滑块的不对称性与基础旁侧土体的强度，提出临坡地基坡面破坏和坡底破坏下单侧非对称破坏模式，构建虚拟滑动面以反映坡后土体的强度贡献，进而建立临坡地基新的Meyerhof承载力解答，给出具体应用步骤并开展理论退化分析，最后结合文献[8，9]的模型试验和文献[4]的数值模拟进行正确性验证。
1. 非对称破坏模式
本文在坡角η≤45°、边坡高度H≤8 m的范围内，开展条形基础下临坡地基承载力的公式推导，以避免边坡发生失稳。
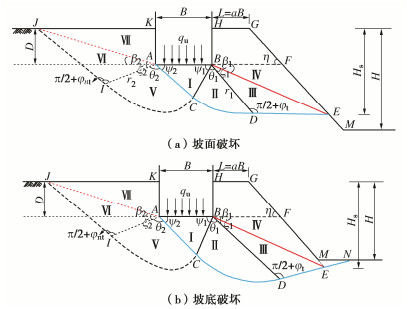
图 1为某临坡条形基础，宽度为B、埋深为D，基础至坡肩的水平距离为L=aB，a为距离系数；地基发生极限平衡状态下整体剪切破坏而达到承载力qu，破坏模式为图 1（a）中的坡面破坏或图 1（b）中的坡底破坏（将坡脚破坏视为坡底破坏的特例）。鉴于临坡基础下土体应力不均匀诱发地基非对称性破坏，设定虚拟滑动面CIJ，将滑动区域分块并做如下假定：
（1）地基滑动面与坡面或其延长线交点至地表的垂直距离为Hs，图 1（a）中滑动面相交坡面GM于E点，此时Hs < H，地基发生坡面破坏；图 1（b）中滑动面相交坡底于N点、相交坡面GM的延长线于E点，此时Hs≥H，地基发生坡底破坏。
（2）土体抗剪强度${\tau _{\text{f}}}$采用基于统一强度理论的平面应变强度方程，其表达式为[6-7]
$$ \left.\begin{array}{l}{\tau }_{\text{f}}={c}_{\text{t}}+\sigma \mathrm{tan}{\varphi }_{\text{t}}\text{，}\\ \text{sin}{\varphi }_{\text{t}}=\frac{2(1+b)\mathrm{sin}\varphi }{2+b(1+\mathrm{sin}\varphi )}\text{，}\\ {c}_{\text{t}}=\frac{2(1+b)c\mathrm{cos}\varphi }{2+b(1+\mathrm{sin}\varphi )}\frac{1}{\mathrm{cos}{\varphi }_{\text{t}}}。\end{array}\right\} $$ (1) 式中：σ为沿滑动面法向的正应力，并以压应力为正；c为黏聚力，φ为内摩擦角；ct为统一黏聚力，φt为统一内摩擦角；b为统一强度理论参数，且0≤b≤1。参数b的取值反映了土体强度中间主应力效应的强弱，同时也代表选取不同的强度准则。当b=0时，式（1）退化为基于经典Mohr-Coulomb强度准则的平面应变强度方程，b=1时退化为基于双剪应力强度准则的平面应变强度方程，0 < b < 1时为一系列新的平面应变强度方程。
（3）坡后土体强度发挥不充分，引入发挥系数n（0 < n≤1）以表征坡后土体强度参数（即虚拟黏聚力cnt和虚拟内摩擦角φnt），则坡后土体抗剪强度${\tau _{n{\text{f}}}}$为
$$ \left.\begin{array}{l}{\tau }_{n\text{f}}=n{c}_{\text{t}}+n\sigma \mathrm{tan}{\varphi }_{\text{t}}={c}_{n\text{t}}+\sigma \mathrm{tan}{\varphi }_{n\text{t}}\text{，}\\ {c}_{n\text{t}}=n{c}_{\text{t}}\text{，}\\ \mathrm{tan}{\varphi }_{n\text{t}}=n\mathrm{tan}{\varphi }_{\text{t}}。\end{array}\right\} $$ (2) （4）在非对称的三角形弹性楔体即区域Ⅰ中，BC面、AC面与水平面的夹角分别为ψ1，ψ2，其大小为$ {\psi _1} = {\varphi _{\text{t}}} $，$ {\psi _2} = {\varphi _{n{\text{t}}}} $（基底完全粗糙），$ {\psi _1} = {{\rm{\mathsf{π}}}/}4 + {\varphi _{\text{t}}}{\text{/}}2 $，$ {\psi _2} = {{\rm{\mathsf{π}}}/}4 + {\varphi _{n{\text{t}}}}{\text{/}}2 $（基底完全光滑）。区域Ⅱ和Ⅴ为剪切过渡区，CD面、CI面分别是辐射区顶角为θ1和θ2的对数螺旋线。
（5）区域Ⅲ和Ⅵ为被动破坏区，分别沿对数螺旋线CD和CI的切线方向滑动，则BD面与DE面的夹角为$ {{\rm{\mathsf{π}}}/}2 + {\varphi _{\text{t}}} $，AI面与IJ面的夹角为$ {{\rm{\mathsf{π}}}/}2 + {\varphi _{n{\text{t}}}} $。区域Ⅳ，Ⅶ为松动区，需对应借助BE面和AJ面上的等代应力反映基础旁侧土体的强度贡献。
2. 公式推导
基于Meyerhof理论，将临坡地基承载力qu近似视为以下两部分之和：由土体黏聚力c和基础旁侧荷载引起的承载力qu1，由土体自重$ \gamma $引起的承载力qu2。
2.1 坡面破坏
图 1（a）为临坡地基的坡面破坏，满足Hs < H。
（1）承载力qu1
设静止土压力系数为K0，则平均作用于图 1（a）中基础侧面BH和AK上的法向应力σa和切应力τa为
$$ \left.\begin{array}{l}{\sigma }_{\text{a}}=0.5{K}_{0}\gamma D\text{，}\\ {\tau }_{\text{a}}={\sigma }_{\text{a}}\mathrm{tan}\delta =0.5{K}_{0}\gamma D\mathrm{tan}\delta 。\end{array}\right\} $$ (3) 式中：δ为基础侧面的外摩擦角（埋深D > 0）。
图 2为隔离体Ⅳ（BEGH）的受力分析，图 2中W4=γS4为隔离体Ⅳ的自重，S4为四边形BEGH的面积，β1为BE面与水平面的夹角。
由BE面法线方向和切线方向的力平衡得法向应力${\sigma _{01}}$和切应力${\tau _{01}}$为
$$ {\sigma _{01}}{\text{ = }}\frac{{\gamma {S_4}\cos {\beta _1} + 0.5{K_0}\gamma {D^2}(\cos {\beta _1}\tan \delta - \sin {\beta _1})}}{{\overline {BE} }}\text{，} $$ (4a) $$ {\tau _{01}}{\text{ = }}\frac{{\gamma {S_4}\sin {\beta _1} + 0.5{K_0}\gamma {D^2}(\sin {\beta _1}\tan \delta + \cos {\beta _1})}}{{\overline {BE} }}。 $$ (4b) 式中：$\overline {BE} = \frac{{\overline {BF} \sin \eta }}{{\sin (\eta - {\beta _1})}} = \frac{{aB\sin \eta + D\cos \eta }}{{\sin (\eta - {\beta _1})}}$；
$$ {S_4} = aBD + \frac{{{D^2}}}{{2\tan \eta }} + \frac{1}{2}\left( {aB + \frac{D}{{\tan \eta }}} \right)\frac{{aB\sin \eta + D\cos \eta }}{{\sin (\eta - {\beta _1})}}\sin {\beta _1}。 $$ 根据上述${\sigma _{01}}$，${\tau _{01}}$先在图 3中定位出点f1，继而通过f1点画出莫尔圆并与强度包线相切于e1点，则e1点坐标即为BD面上的法向应力σb1和切应力τb1；接着过f1点作一条与水平面夹角为β1的直线交莫尔圆于g1点，最后连接e1点、g1点，则图 1（a）中的∠DBE=∠e1g1f1=ζ1，因圆周角是相应圆心角的一半，故∠e1d1f1=2ζ1。
由图 1（a）中三角形BDE的正弦定理，得边长$\overline {BD} $与边长$\overline {BE} $的关系为
$$ \frac{{\overline {BD} }}{{\sin ({{\rm{\mathsf{π}}}/2} - {\varphi _{\text{t}}} - {\zeta _1})}} = \frac{{\overline {BE} }}{{\sin ({{\rm{\mathsf{π}}}/2} + {\varphi _{\text{t}}})}}。 $$ (5) 由图 1（a）中三角形ABC的几何关系得边长$\overline {BC} $为
$$ \overline {BC} = \frac{{B\sin {\psi _2}}}{{\sin ({\psi _1} + {\psi _2})}}。 $$ (6) 假定对数螺旋线CD的矢径${r_1} = \overline {BC} \exp ({\theta _1}\tan {\varphi _{\text{t}}})$，则边长$\overline {BD} $为
$$ \overline {BD} = \overline {BC} {{\text{e}}^{{\theta _1}\tan {\varphi _{\text{t}}}}} = \frac{{B\sin {\psi _2}{{\text{e}}^{{\theta _1}\tan {\varphi _{\text{t}}}}}}}{{\sin {\text{(}}{\psi _1} + {\psi _2}{\text{)}}}}。 $$ (7) 由图 1（a）中的角度关系得
$$ {\theta _1} = {{\rm{\mathsf{π}}}} - {\psi _1} - {\beta _1} - {\zeta _1} 。 $$ (8) 将式（7），（8）和边长$\overline {BE} $代入式（5）得
$$ \mathrm{sin}(\eta -{\beta }_{1})=\frac{\mathrm{sin}({\psi }_{1}+{\psi }_{2})\mathrm{cos}({\varphi }_{\text{t}}+{\zeta }_{1})(aB\mathrm{sin}\eta +D\mathrm{cos}\eta )}{B\mathrm{sin}{\psi }_{2}\mathrm{sin}(\text{π/2}+{\varphi }_{\text{t}}){\text{e}}^{{\theta }_{1}\mathrm{tan}{\varphi }_{\text{t}}}}。 $$ (9) 采用试算法确定角β1，先假定一个角β1，由式（4）计算${\sigma _0}_{\text{1}}$，${\tau _0}_{\text{1}}$；再利用图 3中的几何关系求得角${\zeta _1}$，代入式（9）得到计算角${\beta _1}$。迭代直至假定和计算的角β1相差满足精度$ \Delta = $0.01°的要求。
由图 3中的几何关系得
$$ \begin{array}{l}{\sigma _{\text{b}}}_{\text{1}} = {\sigma _0}_{\text{1}} + &\overline {{d_{\text{1}}}{f_{\text{1}}}} \sin (2{\zeta _{\text{1}}} + {\varphi _{\text{t}}}) - \overline {{d_{\text{1}}}{e_{\text{1}}}} \sin {\varphi _{\text{t}}} \\&={\sigma }_{0}{}_{\text{1}}+\frac{{\tau }_{\text{b1}}}{\mathrm{cos}{\varphi }_{\text{t}}}\left[\mathrm{sin}(2{\zeta }_{\text{1}}+{\varphi }_{\text{t}})-\mathrm{sin}{\varphi }_{\text{t}}\right]。 \end{array}$$ (10) 将${\tau _{{\text{b1}}}} = {c_{\text{t}}} + {\sigma _{{\text{b1}}}}\tan {\varphi _{\text{t}}}$代入式（10）得
$$ {\sigma _{{\text{b1}}}} = \frac{{{\sigma _{01}}{{\cos }^2}{\varphi _{\text{t}}} + {c_{\text{t}}}\cos {\varphi _{\text{t}}}\left[ {\sin (2{\zeta _1} + {\varphi _{\text{t}}}) - \sin {\varphi _{\text{t}}}} \right]}}{{{{\cos }^2}{\varphi _{\text{t}}} - \sin {\varphi _{\text{t}}}\left[ {\sin (2{\zeta _1} + {\varphi _{\text{t}}}) - \sin {\varphi _{\text{t}}}} \right]}}。 $$ (11) 图 4为仅考虑土体黏聚力和基础旁侧荷载时隔离体Ⅱ（BCD）的受力分析，由B点的力矩平衡得法向应力σc1和切应力τc1为
$$ {\sigma _{{\text{c1}}}} = \left[ {({c_{\text{t}}} + {\sigma _{{\text{b1}}}}\tan {\varphi _{\text{t}}}){{\text{e}}^{2{\theta _1}\tan {\varphi _{\text{t}}}}} - {c_{\text{t}}}} \right]\cot {\varphi _{\text{t}}}\text{，} $$ (12a) $$ {\tau _{{\text{c1}}}} = {c_{\text{t}}} + {\sigma _{{\text{c1}}}}\tan {\varphi _{\text{t}}} = ({c_{\text{t}}} + {\sigma _{{\text{b1}}}}\tan {\varphi _{\text{t}}}){{\text{e}}^{2{\theta _1}\tan {\varphi _{\text{t}}}}}。 $$ (12b) ![]()
图 4 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅱ受力分析Figure 4. Force analysis of isolator Ⅱ considering soil cohesion and lateral load of foundation图 5为隔离体Ⅶ（AJK）的受力分析，同理得法向应力${\sigma _{02}}$和切应力${\tau _{02}}$为
$$ {\sigma _{02}} = \frac{1}{2}\gamma D\left( {{K_0}{{\sin }^2}{\beta _2} + \frac{1}{2}{K_0}\tan \delta \sin 2{\beta _2} + {{\cos }^2}{\beta _2}} \right)\text{，} $$ (13a) $$ {\tau _{02}} = \frac{1}{2}\gamma D\left[ {\frac{1}{2}(1 - {K_0})\sin 2{\beta _2} + {K_0}\tan \delta {{\sin }^2}{\beta _2}} \right]。 $$ (13b) 式中：β2为AJ面与水平面的夹角。
类比图 3，画出图 6中AI面极限状态对应的莫尔圆，此时∠IAJ=∠e2g2f2=ζ2，圆心角∠e2d2f2=2ζ2。
由图 1（a）中三角形AIJ的正弦定理，得边长$\overline {AJ} $与边长$\overline {AI} $的关系为
$$ \frac{{\overline {AJ} }}{{\sin ({{\rm{\mathsf{π}}}/2} + {\varphi _{n{\text{t}}}})}} = \frac{{\overline {AI} }}{{\sin ({{\rm{\mathsf{π}}}/2} - {\varphi _{n{\text{t}}}} - {\zeta _2})}}。 $$ (14) 由图 1（a）中三角形ABC的几何关系得边长$\overline {AC} $为
$$ \overline {AC} = \frac{{B\sin {\psi _1}}}{{\sin ({\psi _1} + {\psi _2})}}。 $$ (15) 假定对数螺旋线CI的矢径${r_2} = \overline {AC} {\text{exp}}({\theta _2}{\text{tan}}{\varphi _n}_{\text{t}})$，进而边长$\overline {AI} $为
$$ \overline {AI} = \overline {AC} {{\text{e}}^{{\theta _2}\tan {\varphi _{n{\text{t}}}}}} = \frac{{B\sin {\psi _1}{{\text{e}}^{{\theta _2}\tan {\varphi _{n{\text{t}}}}}}}}{{\sin ({\psi _1} + {\psi _2})}} 。 $$ (16) 由图 1（a）中的角度关系得
$$ {\theta _2} = {{\rm{\mathsf{π}}}} + {\beta _2} - {\psi _2} - {\zeta _2} 。 $$ (17) 将式（16），（17）和边长$\overline {AJ} $=D/sinβ2代入式(14)得
$$ \sin {\beta _2} = \frac{{D\sin ({\psi _1} + {\psi _2})\cos ({\varphi _{n{\text{t}}}} + {\zeta _2})}}{{B\sin {\psi _1}\cos {\varphi _{n{\text{t}}}}{{\text{e}}^{{\theta _2}\tan {\varphi _{n{\text{t}}}}}}}}。 $$ (18) 角${\beta _2}$同样根据试算法确定，迭代直至假定和由式（18）计算的角β2相差满足精度$ \Delta = $0.01°的要求。
由图 6中的几何关系得
$$ {\sigma _{\text{b}}}_2 = {\sigma _0}_2 + \overline {{d_2}{f_2}} \sin {\text{(}}2{\zeta _2} + {\varphi _{n{\text{t}}}}{\text{)}} - \overline {{d_2}{e_2}} \sin {\varphi _{n{\text{t}}}}\\\;\;\;\;={\sigma }_{0}{}_{2}+\frac{{\tau }_{\text{b2}}}{\mathrm{cos}{\varphi }_{n\text{t}}}\left[\mathrm{sin}(2{\zeta }_{2}+{\varphi }_{n\text{t}})-\mathrm{sin}{\varphi }_{n\text{t}}\right]。 $$ (19) 将${\tau _{{\text{b2}}}} = {c_{n{\text{t}}}} + {\sigma _{{\text{b2}}}}\tan {\varphi _{n{\text{t}}}}$代入式（19）得
$$ {\sigma _{{\text{b2}}}} = \frac{{{\sigma _{02}}{{\cos }^2}{\varphi _{n{\text{t}}}} + {c_{n{\text{t}}}}\cos {\varphi _{n{\text{t}}}}\left[ {\sin (2{\zeta _2} + {\varphi _{n{\text{t}}}}) - \sin {\varphi _{n{\text{t}}}}} \right]}}{{{{\cos }^2}{\varphi _{n{\text{t}}}} - \sin {\varphi _{n{\text{t}}}}\left[ {\sin (2{\zeta _2} + {\varphi _{n{\text{t}}}}) - \sin {\varphi _{n{\text{t}}}}} \right]}}。 $$ (20) 图 7为仅考虑土体黏聚力和基础旁侧荷载时隔离体Ⅵ（ACI）的受力分析，由A点的力矩平衡得法向应力${\sigma _{{\text{c2}}}}$和切应力${\tau _{{\text{c2}}}}$为
$$ {\sigma _{{\text{c2}}}} = \left[ {({c_{n{\text{t}}}} + {\sigma _{{\text{b2}}}}\tan {\varphi _{n{\text{t}}}}){{\text{e}}^{2{\theta _2}\tan {\varphi _{n{\text{t}}}}}} - {c_{n{\text{t}}}}} \right]\cot {\varphi _{n{\text{t}}}}\text{，} $$ (21a) $$ {\tau _{{\text{c2}}}} = {c_{n{\text{t}}}} + {\sigma _{{\text{c2}}}}\tan {\varphi _{n{\text{t}}}} = ({c_{n{\text{t}}}} + {\sigma _{{\text{b2}}}}\tan {\varphi _{n{\text{t}}}}){{\text{e}}^{2{\theta _2}\tan {\varphi _{n{\text{t}}}}}}。 $$ (21b) ![]()
图 7 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅵ受力分析Figure 7. Force analysis of isolator Ⅵ considering soil cohesion and lateral load of foundation图 8为仅考虑土体黏聚力和基础旁侧荷载时隔离体Ⅰ（ABC）的受力分析，由其竖直向的力平衡得
$$ {\text{ }}B{q_{{\text{u1}}}} - {\sigma _{{\text{c1}}}}\overline {BC} \cos {\psi _1} - {\tau _{{\text{c1}}}}\overline {BC} \sin {\psi _1}\\ \;\;\;\;\;\;\;\;\;\;={\sigma }_{\text{c2}}\overline{AC}\mathrm{cos}{\psi }_{2}+{\tau }_{\text{c2}}\overline{AC}\mathrm{sin}{\psi }_{2}。 $$ (22) ![]()
图 8 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅰ受力分析Figure 8. Force analysis of isolator Ⅰ considering soil cohesion and lateral load of foundation将式（12），（21）代入式（22）得承载力qu1为
$$ {q_{{\text{u}}1}} = {c_{\text{t}}}{N_{c1}} + {c_{n{\text{t}}}}{N_{c2}} + {\sigma _{01}}{N_{q1}} + {\sigma _{02}}{N_{q2}}。 $$ (23) 式中：Nc1，Nc2为黏聚力承载力系数；Nq1，Nq2为超载承载力系数。
$$ {N_{c1}} = \frac{{{{\cos }^2}{\varphi _{\text{t}}}\sin {\psi _2}(\cot {\varphi _{\text{t}}}\cos {\psi _1} + \sin {\psi _1}){{\text{e}}^{2{\theta _1}\tan {\varphi _{\text{t}}}}}}}{{\sin ({\psi _1} + {\psi _2})\left[ {1 - \sin {\varphi _{\text{t}}}\sin (2{\zeta _1} + {\varphi _{\text{t}}})} \right]}} - $$ $$ \frac{\mathrm{cot}{\varphi }_{\text{t}}\mathrm{sin}{\psi }_{2}\mathrm{cos}{\psi }_{1}}{\mathrm{sin}({\psi }_{1}+{\psi }_{2})}\text{ }\text{，} $$ (24a) $$ {N_{c2}} = \frac{{{{\cos }^2}{\varphi _{n{\text{t}}}}\sin {\psi _1}(\cot {\varphi _{n{\text{t}}}}\cos {\psi _2} + \sin {\psi _2}){{\text{e}}^{2{\theta _2}\tan {\varphi _{n{\text{t}}}}}}}}{{\sin ({\psi _1} + {\psi _2})\left[ {1 - \sin {\varphi _{n{\text{t}}}}\sin (2{\zeta _2} + {\varphi _{n{\text{t}}}})} \right]}} - $$ $$ \text{ }\frac{\mathrm{cot}{\varphi }_{n\text{t}}\mathrm{sin}{\psi }_{1}\mathrm{cos}{\psi }_{2}}{\mathrm{sin}({\psi }_{1}+{\psi }_{2})}\text{，} $$ (24b) $$ {N_{q1}} = \frac{{\sin 2{\varphi _{\text{t}}}\sin {\psi _2}(\cot {\varphi _{\text{t}}}\cos {\psi _1} + \sin {\psi _1}){{\text{e}}^{2{\theta _1}\tan {\varphi _{\text{t}}}}}}}{{2\sin ({\psi _1} + {\psi _2})\left[ {1 - \sin {\varphi _{\text{t}}}\sin (2{\zeta _1} + {\varphi _{\text{t}}})} \right]}}\text{，} $$ (25a) $$ {N_{q2}} = \frac{{\sin 2{\varphi _{n{\text{t}}}}\sin {\psi _1}{\text{(}}\cot {\varphi _{n{\text{t}}}}\cos {\psi _2} + \sin {\psi _2}{\text{)}}{{\text{e}}^{2{\theta _2}\tan {\varphi _{n{\text{t}}}}}}}}{{2\sin ({\psi _1} + {\psi _2})\left[ {1 - \sin {\varphi _{n{\text{t}}}}\sin (2{\zeta _2} + {\varphi _{n{\text{t}}}})} \right]}} 。 $$ (25b) 由图 8中C点的力矩平衡得
$$ \frac{1}{2}{\sigma _{{\text{c1}}}}{\overline {BC} ^2} + {q_{{\text{u1}}}}B(\overline {AC} \cos {\psi _2} - B{\text{/}}2) - \frac{1}{2}{\sigma _{{\text{c2}}}}{\overline {AC} ^2}{\text{ = }}0。 $$ (26) 采用Excel规划法求解式（26）得到发挥系数n。
（2）承载力qu2
图 9为隔离体Ⅲ（BDE）在仅考虑土体自重时的受力分析，图 9中${\varepsilon _1}$为BD面与竖直线的夹角；Ep1，Ep2分别为DE面和BD面上合力的反力，作用点距D点$\overline {DE} $/3、$\overline {BD} $/3，方向与DE面和BD面法线的夹角均为φt；S3为三角形BDE的面积，W3=γS3为隔离体Ⅲ的自重。
由图 9中的角度关系得
$$ {\varepsilon _1} = {{\rm{\mathsf{π}}}}/2 - {\beta _1} - {\zeta _1} 。 $$ (27) 由隔离体Ⅲ水平向和竖直向的力平衡，得反力Ep2为
$$ {E_{{\text{p}}2}} = \frac{{\gamma {S_3}\sin {\varepsilon _1}}}{{\cos {\varphi _{\text{t}}}}}。 $$ (28) 式中：${S_3} = \frac{{B\sin {\psi _2}\sin {\zeta _1}{\text{(}}aB{\text{sin}}\eta {\text{ + }}D{\text{cos}}\eta {\text{)}}{{\text{e}}^{{\theta _1}\tan {\varphi _{\text{t}}}}}}}{{2\sin ({\psi _1} + {\psi _2})\sin (\eta - {\beta _1})}}$。
图 10为隔离体Ⅱ（BCD）在仅考虑土体自重时的受力分析，图中S2为三角形BCD的面积；W2=γS2为隔离体Ⅱ的自重，到B点的力臂为λ1；Ep3为BC面上反力的合力，作用点距C点$\overline {BC} $/3，方向与BC面法线的夹角为φt；F1为CD面上指向B点的径向合力。
由B点的力矩平衡得反力Ep3为
$$ {E_{{\text{p3}}}} = {E_{{\text{p2}}}}{{\text{e}}^{{\theta _1}\tan {\varphi _{\text{t}}}}} + \frac{{3{\lambda _1}\gamma {S_2}}}{{2\overline {BC} \cos {\varphi _{\text{t}}}}}。 $$ (29) 式中：${S_2} = \frac{{{{\overline {BC} }^2}({{\text{e}}^{2{\theta _1}\tan {\varphi _{\text{t}}}}} - 1)}}{{4\tan {\varphi _{\text{t}}}}}$；$ \lambda_{1}=y_{1} \sin \psi_{1}-x_{1} \cos \psi_{1} $；
$$ {x_1} = \frac{{{{\text{e}}^{3{\theta _1}\tan {\varphi _{\text{t}}}}}(\sin {\theta _1} + 3\tan {\varphi _{\text{t}}}\cos {\theta _1}) - 3\tan {\varphi _{\text{t}}}}}{{3(1 + 9{{\tan }^2}{\varphi _{\text{t}}})({e^{2{\theta _1}\tan {\varphi _{\text{t}}}}} - 1)}} \times 4\tan {\varphi _{\text{t}}}\overline {BC} \text{；}\\ {y_1} = \frac{{{\text{4tan}}{\varphi _{\text{t}}}[{{\text{e}}^{3{\theta _1}\tan {\varphi _{\text{t}}}}}(3\tan {\varphi _{\text{t}}}\sin {\theta _1} - \cos {\theta _1}) + 1]}}{{3(1 + 9{{\tan }^2}{\varphi _{\text{t}}})({e^{2{\theta _1}\tan {\varphi _{\text{t}}}}} - 1)}}\overline {BC} 。 $$ 图 11为隔离体Ⅵ（AIJ）在仅考虑土体自重时的受力分析，图中${\varepsilon _{\text{2}}}$为AI面与竖直线的夹角；Ep4，Ep5分别为IJ面和AI面上合力的反力，作用点距I点$\overline {IJ} $/3，$\overline {AI} $/3，方向与IJ面和AI面法线的夹角均为${\varphi _{n{\text{t}}}}$；S6为三角形AIJ的面积，W6=γS6为隔离体Ⅵ的自重。
由图 11中的角度关系得
$$ {\varepsilon _2} = {{\rm{\mathsf{π}}}}/2 + {\beta _2} - {\zeta _2} 。 $$ (30) 由隔离体Ⅵ水平向和竖直向的力平衡，得反力Ep5为
$$ {E_{{\text{p5}}}} = \frac{{\gamma {S_6}\sin {\varepsilon _2}}}{{\cos {\varphi _{n{\text{t}}}}}}。 $$ (31) 式中：${S_6} = \frac{{BD\sin {\psi _1}\sin {\zeta _2}{{\text{e}}^{{\theta _2}\tan {\varphi _{n{\text{t}}}}}}}}{{2\sin {\beta _2}\sin ({\psi _1} + {\psi _2})}}$。
图 12为隔离体Ⅴ（ACI）在仅考虑土体自重时的受力分析，图 12中S5为三角形ACI的面积；W5=γS5为隔离体Ⅴ的自重，到A点的力臂为${\lambda _2}$；Ep6为AC面上反力的合力，作用点距C点$\overline {AC} $/3，方向与AC面法线的夹角为${\varphi _{n{\text{t}}}}$；F2为CI面上指向A点的径向合力。
由A点的力矩平衡得反力Ep6为
$$ {E_{{\text{p6}}}} = {E_{{\text{p5}}}}{{\text{e}}^{{\theta _2}\tan {\varphi _{n{\text{t}}}}}} + \frac{{3{\lambda _2}{W_5}}}{{2\overline {AC} \cos {\varphi _{n{\text{t}}}}}}。 $$ (32) 式中：${S_5} = \frac{{{{\overline {AC} }^2}({{\text{e}}^{2{\theta _2}\tan {\varphi _{n{\text{t}}}}}} - 1)}}{{4\tan {\varphi _{n{\text{t}}}}}}$；$ \lambda_{2}=y_{2} \sin \psi_{2}-x_{2} \cos \psi_{2} $；$ {x}_{2}=\frac{{\text{e}}^{3{\theta }_{2}\mathrm{tan}{\varphi }_{n\text{t}}}(\mathrm{sin}{\theta }_{2}+3\mathrm{tan}{\varphi }_{n\text{t}}\mathrm{cos}{\theta }_{2})-3\mathrm{tan}{\varphi }_{n\text{t}}}{3(1+9{\mathrm{tan}}^{2}{\varphi }_{n\text{t}})({\text{e}}^{2{\theta }_{2}\mathrm{tan}{\varphi }_{n\text{t}}}-1)}\times 4\mathrm{tan}{\varphi }_{n\text{t}}\overline{AC}； $$ {y}_{2}=\frac{{\text{e}}^{3{\theta }_{2}\mathrm{tan}{\varphi }_{n\text{t}}}(3\mathrm{tan}{\varphi }_{n\text{t}}\mathrm{sin}{\theta }_{2}-\mathrm{cos}{\theta }_{2})+1}{3(1+9{\mathrm{tan}}^{2}{\varphi }_{n\text{t}})({\text{e}}^{2{\theta }_{2}\mathrm{tan}{\varphi }_{n\text{t}}}-1)}\times 4\mathrm{tan}{\varphi }_{n\text{t}}\overline{AC}。 $
图 13为隔离体Ⅰ（ABC）在考虑土体自重时的受力分析，图中S1为三角形ABC的面积，W1=γS1为隔离体Ⅰ的自重。由隔离体Ⅰ竖直向的力平衡得
$$ \left.\begin{array}{l}{q}_{\text{u}2}B={E}_{\text{p3}}\mathrm{cos}({\psi }_{1}-{\varphi }_{\text{t}})-{E}_{\text{p6}}\mathrm{cos}({\psi }_{2}-{\varphi }_{n\text{t}})-{W}_{\text{1}}\text{，}\\ {S}_{1}=\frac{{B}^{2}\mathrm{sin}{\psi }_{1}\mathrm{sin}{\psi }_{2}}{2\mathrm{sin}({\psi }_{1}+{\psi }_{2})}。\end{array}\right\} $$ (33) 将式（29），（32）代入式（33），得承载力qu2为
$$ {q_{{\text{u}}2}} = \frac{1}{2}\gamma B{N_\gamma }。 $$ (34) 式中：Nγ为重度承载力系数，
$$ \begin{gathered} {N_\gamma } = \frac{{4{S_3}\sin {\varepsilon _1}{{\text{e}}^{{\theta _1}\tan {\varphi _{\text{t}}}}}\cos ({\psi _1} - {\varphi _{\text{t}}})}}{{{B^2}\cos {\varphi _{\text{t}}}}} + \frac{{12{S_2}{\lambda _1}\cos {\psi _1}}}{{{B^3}\cos {\varphi _{\text{t}}}}} \cdot \hfill \\ {\text{ }}\frac{{\cos ({\psi _1} - {\varphi _{\text{t}}})}}{{{B^3}\cos {\varphi _{\text{t}}}}} + \frac{{4{S_6}\sin {\varepsilon _2}{{\text{e}}^{{\theta _2}\tan {\varphi _{n{\text{t}}}}}}\cos ({\psi _2} - {\varphi _{n{\text{t}}}})}}{{{B^2}\cos {\varphi _{n{\text{t}}}}}} + \hfill \\ \end{gathered} $$ $$ \text{ }\frac{12{S}_{5}{\lambda }_{2}\mathrm{cos}{\psi }_{2}\mathrm{cos}({\psi }_{2}-{\varphi }_{n\text{t}})}{{B}^{3}\mathrm{cos}{\varphi }_{n\text{t}}}-\frac{\mathrm{sin}{\psi }_{1}\mathrm{sin}{\psi }_{2}}{2\mathrm{sin}({\psi }_{1}+{\psi }_{2})}。 $$ (35) （3）总承载力qu
将式（23），（34）相加，得坡面破坏模式下临坡地基的Meyerhof承载力qu为
$$ {q_{\text{u}}} = {c_{\text{t}}}{N_{c1}} + {c_{n{\text{t}}}}{N_{c2}} + {\sigma _{01}}{N_{q1}} + {\sigma _{02}}{N_{q2}} + \frac{1}{2}\gamma B{N_\gamma }。 $$ (36) 2.2 坡底破坏
图 1（b）为临坡地基的坡底破坏，满足Hs≥H。由图 1中的几何关系得
$$ {H_{\text{s}}} = \frac{{D\sin \eta \cos {\beta _1} + L\sin \eta \sin {\beta _1}}}{{\sin (\eta - {\beta _1})}}。 $$ (37) 坡底破坏模式下临坡地基承载力公式的推导与2.1节类似，只是区别于如何确定BE面上的法向应力$ {\sigma '_{01}} $和切应力$ {\tau '_{01}} $。图 14为隔离体Ⅳ（BENMGH）的受力分析，图中$ {S'_4} $为多边形BENMGH的面积，${W'_4} = \gamma {S'_4}$为隔离体Ⅳ的自重；σd，τd为EN面上的法向应力和切应力。由BE面法线方向和切线方向的力平衡得法向应力$ {\sigma '_{01}} $和切应力$ {\tau '_{01}} $为
$$ {\sigma '_{01}}{\text{ = }}\frac{{{{W'}_4}\cos {\beta _1} + 0.5{K_0}\gamma {D^2}(\cos {\beta _1}\tan \delta - \sin {\beta _1})}}{{\overline {BE} }} - $$ $$ \text{ }\frac{{\sigma }_{\text{d}}\overline{EN}\mathrm{sin}({\varphi }_{\text{t}}+{\zeta }_{1})-{\tau }_{\text{d}}\overline{EN}\mathrm{cos}({\varphi }_{\text{t}}+{\zeta }_{1})}{\overline{BE}}\text{，} $$ (38a) $$ {\tau '_{01}}{\text{ = }}\frac{{{{W'}_4}\sin {\beta _1} + 0.5{K_0}\gamma {D^2}(\sin {\beta _1}\tan \delta + \cos {\beta _1})}}{{\overline {BE} }} - $$ $$ \text{ }\frac{{\sigma }_{\text{d}}\overline{EN}\mathrm{cos}({\varphi }_{\text{t}}+{\zeta }_{1})+{\tau }_{\text{d}}\overline{EN}\mathrm{sin}({\varphi }_{\text{t}}+{\zeta }_{1})}{\overline{BE}}\text{，} $$ (38b) 式中：$\overline {EN} = \overline {ME} \frac{{\sin \eta }}{{\sin ({{\rm{\mathsf{π}}}/}2 - {\varphi _{\text{t}}} - {\zeta _1} - {\beta _1})}}$；
$$ \overline {ME} = \frac{{(aB\sin \eta + D\cos \eta )\sin {\beta _1} - (H - D)\sin (\eta - {\beta _1})}}{{\sin (\eta - {\beta _1})\sin \eta }}； $$ $$ \overline {MN} = \overline {ME} \frac{{\sin ({{\rm{\mathsf{π}}}/}2 + {\varphi _{\text{t}}} + {\zeta _1} + {\beta _1} - \eta )}}{{\sin ({{\rm{\mathsf{π}}}/}2 - {\varphi _{\text{t}}} - {\zeta _1} - {\beta _1})}}\text{；} $$ $$ \begin{array}{l}{{S}^{\prime }}_{4}=aBD+\frac{{D}^{2}}{2\mathrm{tan}\eta }+\frac{1}{2}\left(aB+\frac{D}{\mathrm{tan}\eta }\right)\overline{BE}\mathrm{sin}{\beta }_{1}+\\ \;\;\;\;\text{ }\frac{1}{2}\overline{ME}\overline{MN}\mathrm{sin}\eta \text{ }。\end{array} $$ 图 15为隔离体Ⅲ在仅考虑土体黏聚力和基础旁侧荷载时的受力分析。由DE面法线方向和切线方向的力平衡得
$${\sigma _{\text{d}}}\overline {DE} - {\sigma '_{01}}\overline {BE} \sin ({\varphi _{\text{t}}} + {\zeta _1}) - {\tau '_{01}}\overline {BE} \cos ({\varphi _{\text{t}}} + {\zeta _1})\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {\tau _{{\text{b}}1}}\overline {BD} \cos {\varphi _{\text{t}}} - {\sigma _{{\text{b}}1}}\overline {BD} \sin {\varphi _{\text{t}}}\text{，} $$ (39a) $${\tau _{\text{d}}}\overline {DE} - {\sigma '_{01}}\overline {BE} \cos ({\varphi _{\text{t}}} + {\zeta _1}) - {\tau '_{01}}\overline {BE} \sin ({\varphi _{\text{t}}} + {\zeta _1})\\\;\;\;\;\;\;\;\;\;\; = {\tau _{{\text{b}}1}}\overline {BD} \sin {\varphi _{\text{t}}} - {\sigma _{{\text{b}}1}}\overline {BD} \cos {\varphi _{\text{t}}}。 $$ (39b) ![]()
图 15 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅲ受力分析Figure 15. Force analysis of isolator Ⅲ considering soil cohesion and lateral load of foundation结合式（38），（39）迭代计算法向应力$ {\sigma '_{01}} $、切应力$ {\tau '_{01}} $，其余分析过程详见2.1节，同样相加得坡底破坏模式下临坡地基的Meyerhof承载力qu为
$$ {q_{\text{u}}} = {c_{\text{t}}}{N_{c1}} + {c_{n{\text{t}}}}{N_{c2}} + {\sigma '_{01}}{N_{q1}} + {\sigma _{02}}{N_{q2}} + \frac{1}{2}\gamma B{N_\gamma }。 $$ (40) 2.3 应用步骤
（1）假定地基发生坡面破坏，由试算法迭代求出角β1。
（2）由式（37）求出距离Hs，以判断临坡地基的破坏模式。
（3）当Hs < H时，按照坡面破坏模式继续进行计算，由试算法迭代求出角β2，并得到σ01，σ02，ζ1，ζ2，由式（36）确定临坡地基承载力。
（4）当Hs≥H时，按照坡底破坏模式由试算法迭代重新计算，由式（40）确定临坡地基承载力。
2.4 理论退化
针对临坡地基坡面破坏和坡底破坏两种非对称破坏模式，采用统一强度理论所建立的临坡地基Meyerhof承载力新解即式（36），（40），综合考虑了中间主应力（参数0≤b≤1）、基础至坡肩的水平距离、边坡高度和基底粗糙情况等因素，可更好地展现临坡地基的承载性能，具有重要的理论价值。式（36），（40）在参数b=0时为基于Mohr-Coulomb强度准则的临坡地基Meyerhof承载力解答，参数b=1时为基于双剪应力强度准则的临坡地基Meyerhof承载力解答，在0 < b < 1时能获得一系列新的临坡地基承载力解答，以适应临坡地基实际非对称破坏。
3. 对比验证
将本文非对称破坏模式下临坡地基Meyerhof承载力新解（即式（36），（40））与文献[8，9]的模型试验和文献[4]的数值模拟进行比较，以验证所得临坡地基承载力公式的正确性。
3.1 模型试验
模型试验Ⅰ：Keskin等[8]通过室内模型试验获得了基底光滑条件下砂性土边坡坡顶条形基础的地基承载力，试验测得土体的黏聚力c=0.1 kPa，内摩擦角φ=41.8°，平均干重度=17 kN/m3，B=0.07 m，D=0 m，η=30°，H=0.5 m，属于Hs < H的坡面破坏。
图 16为文献[8]临坡地基承载力模型试验与本文基底完全光滑下式（36）的对比，可以看出：式（36）与模型试验所得临坡地基承载力qu均随基础至坡肩水平距离系数a的增加明显增大；b=0.6时式（36）与文献[8]的模型试验实测值相差较小，平均相对误差绝对值为5.5%，验证了式（36）的有效性；同时，不考虑中间主应力（b=0）时的式（36）偏小，低估了地基的实际承载潜能，而b=1时的式（36）偏大，又夸大了土体强度的中间主应力效应。
![]()
模型试验Ⅱ：Castelli等[9]开展室内模型试验探讨了基础位置对基底光滑条件下砂性土边坡坡顶条形基础的地基承载力。试验测得土体的内摩擦角φ=38°，最大干重度=17.5 kN/m3，但未给出黏聚力大小，计算时取c=0.1 kPa，η=30°，H=0.28 m，属于Hs < H的坡面破坏。
表 1为文献[9]临坡地基模型试验与本文基底完全光滑下式（36）的对比，可以看出：b=0.75时式（36）与文献[9]的模型试验实测值吻合良好，平均相对误差绝对值为7.1%，验证了式（36）的正确性；另外，b=0时式（36）较实测值偏小，但b=1时又偏大。
表 1 对比文献[9]的临坡地基模型试验Table 1. Comparison with model tests for foundations near slopes of Reference [9]B/m D/m a qu试验/kPa qu式(36) /kPa b=0 b=0.75 b=1 0.04 0 3.5 65.67 42.10 66.43 78.43 0.04 0 7.0 79.00 60.12 93.88 108.89 0.06 0 2.2 88.26 50.73 83.00 99.82 0.06 0 4.5 136.37 73.45 129.92 148.55 平均相对误差绝对值/% 61.8 7.1 15.9 3.2 数值模拟
郑刚等[4]采用不连续布局优化数值法分析了临坡条形基础下地基承载力，土体屈服满足Mohr-Coulomb强度准则，参数取值：B=2 m，D=0 m，L=0 m，η=10°；c=40 kPa，φ=40°，γ=20 kN/m3。
图 17为文献[4]临坡地基数值模拟与本文b=0时式（36），（40）的对比，其中破坏模式为本文采用相同数值模拟方法获得的，可以看出：式（36），（40）与数值模拟对应的临坡地基承载力qu均随边坡高度H增加先减小后恒定，平均相对误差绝对值为3.4%，验证了式（36），（40）的合理性；由式（37）判定的临坡地基破坏模式与补充的数值模拟结果相一致。
![]()
4. 结论
（1）结合滑动面与坡面的相交位置及三角形楔体的非对称，构建了临坡地基坡面非对称破坏模式和坡底非对称破坏模式，可合理反映坡后土体的强度贡献，与临坡地基的真实破坏机制更为符合。
（2）所得临坡地基新的Meyerhof承载力解答综合考虑了中间主应力、基础至坡肩的水平距离、边坡高度和基底粗糙情况等因素，可退化为Mohr-Coulomb强度准则解答、双剪应力强度准则解答以及一系列新解答，具有重要的理论意义。
（3）本文解答与文献模型试验和数值模拟均吻合良好，验证了所得临坡地基Meyerhof承载力公式的正确性。临坡地基承载力的中间主应力效应显著且随边坡高度增加先减小后恒定，未考虑中间主应力的地基承载力偏小。
-
![]()
图 4 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅱ受力分析
Figure 4. Force analysis of isolator Ⅱ considering soil cohesion and lateral load of foundation
![]()
图 7 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅵ受力分析
Figure 7. Force analysis of isolator Ⅵ considering soil cohesion and lateral load of foundation
![]()
图 8 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅰ受力分析
Figure 8. Force analysis of isolator Ⅰ considering soil cohesion and lateral load of foundation
![]()
图 15 考虑土体黏聚力和基础旁侧荷载的隔离体Ⅲ受力分析
Figure 15. Force analysis of isolator Ⅲ considering soil cohesion and lateral load of foundation
![]()
![]()
表 1 对比文献[9]的临坡地基模型试验
Table 1 Comparison with model tests for foundations near slopes of Reference [9]
B/m D/m a qu试验/kPa qu式(36) /kPa b=0 b=0.75 b=1 0.04 0 3.5 65.67 42.10 66.43 78.43 0.04 0 7.0 79.00 60.12 93.88 108.89 0.06 0 2.2 88.26 50.73 83.00 99.82 0.06 0 4.5 136.37 73.45 129.92 148.55 平均相对误差绝对值/% 61.8 7.1 15.9 
下载: 导出CSV
-
[1] MEYERHOF G G, HANNA A. Ultimate bearing capacity of foundations on layered soils under inclined load[J]. Canadian Geotechnical Journal, 1978, 15(4): 565-572. doi: 10.1139/t78-060
[2] 胡卫东, 曹文贵. 基于Meyerhof理论的临坡地基极限承载力简化分析方法[J]. 湖南大学学报(自然科学版), 2015, 42(1): 81-89. https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201501012.htm HU Weidong, CAO Wengui. A simplified analysis method for the ultimate bearing capacity of ground foundation near slope based on the theory of Meyerhof[J]. Journal of Hunan University (Natural Sciences), 2015, 42(1): 81-89. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201501012.htm
[3] JIN L X, FENG Y W, ZHANG H C, et al. The use of improved radial movement optimization to calculate the ultimate bearing capacity of a nonhomogeneous clay foundation adjacent to slopes[J]. Computers and Geotechnics, 2020, 118: 103338. doi: 10.1016/j.compgeo.2019.103338
[4] 郑刚, 于晓旋, 杜娟, 等. 临近边坡的条形基础地基极限承载力数值分析[J]. 岩土力学, 2018, 39(10): 3812-3820, 3829. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810039.htm ZHENG Gang, YU Xiaoxuan, DU Juan, et al. Numerical analysis of ultimate bearing capacity of strip footings near slopes[J]. Rock and Soil Mechanics, 2018, 39(10): 3812-3820, 3829. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810039.htm
[5] CHEN T J, XIAO S G. An upper bound solution to undrained bearing capacity of rigid strip footings near slopes[J]. International Journal of Civil Engineering, 2020, 18(4): 475-485. doi: 10.1007/s40999-019-00463-w
[6] 俞茂宏. 岩土类材料的统一强度理论及其应用[J]. 岩土工程学报, 1994, 16(2): 1-10. http://cge.nhri.cn/cn/article/id/9755 YU Maohong. Unified strength theory for geomaterials and lts applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(2): 1-10. (in Chinese) http://cge.nhri.cn/cn/article/id/9755
[7] 俞茂宏, 武霞霞, 史俊, 等. 确定土体破坏准则的一个新方法[J]. 西安交通大学学报, 2020, 54(8): 1-10. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJT202008002.htm YU Maohong, WU Xiaxia, SHI Jun, et al. A new strategy for determining failure criteria of soil[J]. Journal of Xi'an Jiaotong University, 2020, 54(8): 1-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJT202008002.htm
[8] KESKIN M S, LAMAN M. Model studies of bearing capacity of strip footing on sand slope[J]. KSCE Journal of Civil Engineering, 2013, 17(4): 699-711. doi: 10.1007/s12205-013-0406-x
[9] CASTELLI F, LENTINI V. Evaluation of the bearing capacity of footings on slopes[J]. International Journal of Physical Modelling in Geotechnics, 2012, 12(3): 112-118. doi: 10.1680/ijpmg.11.00015
-
其他相关附件
计量
- 文章访问数: 286
- HTML全文浏览量: 26
- PDF下载量: 85
