冻融循环作用下砂岩的力学特性及细观损伤本构模型研究

肖鹏; 陈有亮; 杜曦; 王苏然

doi:10.11779/CJGE20220219

冻融循环作用下砂岩的力学特性及细观损伤本构模型研究 English Version

肖鹏^{1, 2,},
陈有亮^2, ,,
杜曦³,
王苏然⁴

1.
东南大学交通学院岩土工程研究所, 江苏南京 210096
2.
上海理工大学环境与建筑学院土木工程系, 上海 200093
3.
新南威尔士大学土木与环境工程学院, 悉尼 2052
4.
同济大学地下建筑与工程系, 上海 200093

基金项目:

国家自然科学基金项目 10872133

上海市软科学研究领域重点项目 18692106100

详细信息

作者简介:
肖鹏(1997—)，男，博士研究生，主要从事岩石力学、微生物矿化研究。E-mail：xiaopeng_seu@163.com

通讯作者:
陈有亮, E-mail：chenyouliang2001@163.com

中图分类号: TU411;TD313
计量
- 文章访问数: 472
- HTML全文浏览量: 106
- PDF下载量: 165
出版历程
- 收稿日期: 2022-03-01
- 网络出版日期: 2023-04-16
- 刊出日期: 2023-03-31

Mechanical properties of sandstone under freeze-thaw cycles and studies on meso-damage constitutive model

XIAO Peng^{1, 2,},
CHEN Youliang^2, ,,
DU Xi³,
WANG Suran⁴

1.
Institute of Geotechnical Engineering, Southeast University, Nanjing 210096, China
2.
Department of Civil Engineering, School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China
3.
School of Civil and Environmental Engineering, University of New South Wales, Sydney 2052, Australia
4.
Department of Underground Architecture and Engineering, Tongji University, Shanghai 200093, China

摘要

摘要: 针对寒区岩体工程中岩石的冻融问题，选取砂岩为试样，通过进行室内冻融循环试验、扫描电子显微镜观测和三轴压缩试验对砂岩质量损失、微观结构和力学特性进行了分析。然后基于Lemaitre应变等效假设理论，通过引入能够反映岩石冻融破坏过程中的细观冻融损伤变量和力损伤变量来描述岩石材料的劣化程度及损伤演化规律，并采用连续损伤力学理论，建立了冻融与围压耦合作用下岩石的损伤演化方程及细观损伤本构模型。采用理论推导的方法得出所需的模型参数表达式，最后利用冻融岩石的三轴压缩试验数据对该模型的合理性和准确性进行了验证。将试验曲线的峰值点与模型理论曲线的峰值点进行对比，结果表明两者吻合度较好，该损伤本构模型能够较好地反映岩石三轴压缩过程的应力-应变峰值特性，验证了该模型及模型参数确定方法的合理性与可靠性。该模型拓展了岩石在冻融与围压耦合作用下的损伤模型，进一步的揭示了岩石在冻融与围压耦合作用下的损伤机制和破坏规律。
- 冻融循环 /
- 力学特性 /
- 细观冻融损伤变量 /
- SMP准则 /
- 损伤演化 /
- 本构模型
Abstract: To address the freeze-thaw problems of rocks in cold-zone rock engineering, the sandstone is selected as the specimen and analyzed for mass loss, microstructure and mechanical properties by conducting the cyclic indoor freeze-thaw tests, scanning electron microscope observations and triaxial compression tests. Then, based on the Lemaitre strain equivalence hypothesis theory, the meso-scale freeze-thaw damage variables and force damage variables are introduced to reflect the process of freeze-thaw damage of the rocks to describe the degree of deterioration of rock materials and the damage evolution law. Using the continuous damage mechanics theory, the damage evolution equation and the meso-scale damage constitutive model for the rocks under the coupling of freeze-thaw and cofining pressure are established. The theoretical derivation method is used to obtain the required expressions for model parameters. Finally, the rationality and accuracy of the model are verified by the triaxial compression test data of freeze-thaw of the rocks. The peak points of the test curve are compared with those of the theoretical curve by the model, and the results show that they are in good agreement. The damage constitutive model can better reflect the stress-strain peak characteristics of the rocks during triaxial compression, which verifies the rationality and reliability of the proposed model and the relevant method for determining the model parameters. This model expands the damage model for the rocks under the coupling of freeze-thaw and confining pressure and further reveals their damage mechanism and failure law.
- freeze-thaw cycle /
- mechanical property /
- Meso-freeze-thaw damage variable /
- SMP criterion /
- damage evolution /
- constitutive model

HTML全文

0. 引言

“十三五”以来，中国基础设施建设如火如荼，兴建了诸多重点寒区建设项目，在这些寒区工程的施工过程中遇到了越来越复杂的岩石工程问题，其中大部分寒区工程项目出现的施工问题都与岩石的冻结破坏有关，如：青藏铁路项目、中俄石油管道工程以及中西部数量繁多的隧道项目等。在此类地区进行岩体工程建设，最为常见且严峻的问题就是冻融循环引起的灾害。伴随着“十四五”规划重点项目川藏铁路及沿边铁路等基础设施建设的提出，对寒区工程岩土体结构的稳定性，岩石材料的强度、变形破坏特性等力学性质的研究不可避免地成为了重点项目建设面临的首要问题。

近年来，关于冻融循环对岩石物理力学性能影响方面的研究受到了众多国内外学者的重视，并取得了巨大的进展和丰硕的成果^[1-6]。陈有亮等^[7]选取花岗岩为试样，对其开展了水化学溶液和冻融循环耦合作用下的物理力学试验研究，分析并探讨了冻融循环和水化学溶液耦合作用下岩石的力学特性损伤劣化规律；韩铁林等^[8]对砂岩在不同化学溶液中腐蚀30 d后及再经历不同冻融循环次数作用后的物理力学特征变化规律进行了研究与分析，并基于孔隙率的变化建立了损伤变量来定量的描述试样的损伤劣化程度；张君岳等^[9]以不同冻融循环次数为试验变量，对饱水红砂岩开展了冻融循环试验，分析并探讨了冻融循环次数对红砂岩的物理及力学特性的劣化规律；张慧梅等^[10]基于损伤力学理论，提出了冻融损伤、力损伤与总损伤的概念，定义了冻融损伤变量和力损伤变量，并基于应变等价性原则，建立了冻融与荷载共同作用下岩石的损伤本构关系。研究表明：岩石在冻融与荷载共同作用下的损伤与冻融损伤变量、受荷损伤变量以及两者的耦合有着密切的关系；徐光苗等^[11]基于宏微观损伤力学理论，对由冻融和荷载所产生的损伤分别进行了定量研究, 推导了冻融和荷载耦合作用下岩石的总损伤变量以及损伤本构模型，并与饱和页岩和红砂岩在不同冻融循环次数下的相关试验结果进行了对比；孟祥振等^[12]针对前人已建立的损伤本构模型所存在的局限与不足，在深入研究含孔隙岩石变形破坏特征的基础上，引入孔隙率来定义岩石的冻融体积变化，定义了冻融损伤变量，并采用损伤力学理论，建立了含孔隙岩石的冻融损伤本构模型；杨涛等^[13]重点研究了不同冻融循环次数对砂岩强度的影响规律，并以损伤力学相关理论为基础，定义了综合冻融损伤变量，得到了损伤演化方程的特征曲线，最后建立了砂岩的冻融损伤本构模型。

上述研究工作为正确认识冻融循环下岩石力学性质的变化和损伤规律奠定了良好的基础，但仍存在一些不足，主要表现在以下4点：①目前关于岩石冻融循环的研究成果主要体现在对其宏观力学特性的影响规律方面，从微观变化量出发的研究较少、对微观裂隙的研究从定性的角度进行定量研究也较少。②对岩石冻融损伤理论方面的研究不足，即通过建立冻融损伤本构模型对岩石损伤力学特性的研究较少，且已有的冻融损伤本构模型大多没有考虑围压的作用。③已建立的冻融损伤本构模型基本上都局限于一维条件，且选取的岩石微元强度概率模型及强度准则较为单一。④以往的研究都是以宏观力学损伤理论为基础，通过宏观力学参数如弹性模量、波速等来表征岩石的损伤，从细观上建立岩石在冻融过程中损伤本构模型的研究较为罕见。针对上述问题，还需要做进一步探索。鉴于此，本文基于岩石试样微元强度服从两参数的Weibull分布，引入细观冻融损伤变量和力损伤变量，采用连续损伤力学理论，以SMP准则为岩石强度准则，并基于Lemaitre应变等价性假设理论建立了包含岩石冻融-围压耦合损伤演化方程的细观损伤本构模型，并通过与试验曲线对比验证了该模型。

2. 冻融循环试验概况

2.1 试验仪器及方案

（1）试样制备

该试验材料为钙质砂岩，先从冻融区域现场取得岩块，并根据国际岩石力学学会（ISRM）试验规程，加工制作成用于三轴压缩试验的试样。试样为直径50 mm，高度100 mm的圆柱体试块，如图 1所示。加工完成的试样基本尺寸和精度符合《工程岩体试验方法标准：GB/T50266—2013》的标准。

图 1 砂岩冻融试验试块

Figure 1. Freeze-thaw test block of sandstone

下载: 全尺寸图片幻灯片

（2）试验仪器

TZW-3000Ⅱ岩石真三轴流变试验机，如图 2所示；WGD-501立式冻融机，如图 3所示；COXEM EM30 Plus超高分辨率台式扫描电镜（SEM）；ZBL-U5200超声检测仪；JJ600型电子天平。

图 2 TZW-3000II岩石真三轴流变试验机

Figure 2. TZW-3000II rock true triaxial rheological testing machine

下载: 全尺寸图片幻灯片

图 3 WGD-501立式冻融机

Figure 3. WGD-501 vertical freeze-thaw machine

下载: 全尺寸图片幻灯片

（3）试验方案

将初期筛选出来的16块砂岩试块随机分为4组，并进行质量、纵波波速等参数的测量。将分组编号后的12块试块分组放入WGD-501立式快速冻融试验机中，分别以20℃~-30℃，-40℃，-50℃进行冻融循环80次，每个循环约6 h，其中冻结时间3 h，融化时间3 h，留下一组不做冻融循环试验作为对照组。待冻融循环结束后取出测量砂岩试块的质量、波速等参数，并用扫描电子显微镜观测冻融后岩样的微观结构，最后对所有砂岩试块进行三轴压缩试验。

2.2 试验结果及分析

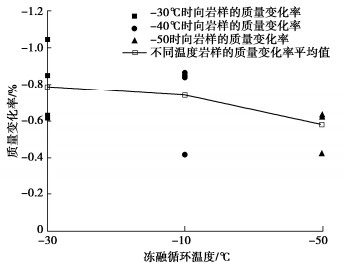
（1）不同冻融循环温度下岩样质量变化率

定义质量变化率 ${\eta _{m{\text{12}}}}$ 如下：

${\eta _{m{\text{12}}}}{\text{ = }}\frac{{{m_2} - {m_1}}}{{{m_1}}} \times 100\% 。$

(1)

式中：m₁为砂岩试样吸水饱和质量（kg）；m₂为砂岩试样经过不同冻结温度循环后的质量（kg）。

不同冻结温度循环作用后岩样的质量变化率，如图 4所示。

图 4 质量变化率随冻融循环温度变化关系曲线

Figure 4. Variation of mass change rate with temperature of freeze-thaw cycle

下载: 全尺寸图片幻灯片

从图 4可以看出：不同冻融循环温度处理前后砂岩岩样的质量变化均呈现下降的趋势，随着冻融循环温度的降低，质量变化率整体上呈现下降趋势。即在此冻融循环试验中，冻融循环温度为-30℃的砂岩岩样质量变化率要高于冻融循环温度为-40℃和-50℃的砂岩岩样质量变化率。质量变化的主要原因是：矿物颗粒吸水膨胀性和收缩性不同引起颗粒间的变形不协调，颗粒间的胶结作用被削弱，颗粒出现脱落及微裂缝；同时，岩石在冻融循环过程中内部会产生作用在内部孔隙壁和试块表面的冻胀力，从而引起砂岩表面的颗粒脱落和片落，并且颗粒脱落和片落的质量要大于新增孔隙内含水的质量，故在冻融循环试验中砂岩试样整体质量表现为下降的趋势。当试样冻融结束升温融化时，试样孔隙中的冰晶体会快速融化，此时孔隙内会形成一个负压区域，由于压强作用外界水分会被吸入试样表面和孔隙中，从而引起岩石质量较冻融结束后有一定的增加，且随着冻融循环温度的降低这种现象愈发明显，即吸入外界环境中水的质量随着冻融循环温度的降低不断增加，故随着冻融循环温度的降低，砂岩质量下降幅度呈现减小的趋势。

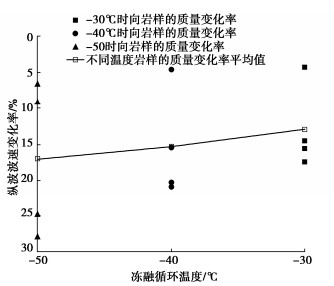
（2）不同冻融循环温度下岩样纵波波速变化率

定义纵波波速变化率 ${\eta _{{V_{{\text{P12}}}}}}$ 如下：

${\eta _{{V_{{\text{P12}}}}}} = \frac{{{V_{{\text{P2}}}} - {V_{{\text{P1}}}}}}{{{V_{{\text{P1}}}}}} \times 100\% 。$

(2)

式中：V_P1为岩样吸水饱和后的纵波波速（m/s）；V_P2为岩样经过不同冻结温度处理后的纵波波速（m/s）。

通过使用ZBL-U5200超声检测仪测量经过不同冻结温度循环前后岩样的纵波波速，得到不同冻结温度循环作用后岩样的纵波波速变化率，如图 5所示。

图 5 纵波波速变化率随冻融循环温度变化关系曲线

Figure 5. Variation of change rate of longitudinal wave velocity with temperature of freeze-thaw cycle

下载: 全尺寸图片幻灯片

从图 5可以看出：不同冻融循环温度作用下砂岩岩样的纵波波速变化均呈现下降的趋势，但随着冻融循环温度的降低，纵波波速变化率整体上呈现上升趋势。冻融循环过程中由于岩石内部水分的交替冻结和融解所形成的冻胀力不断挤压岩石内部的初始孔隙，致使岩石内部的初始孔隙和微裂缝的体积逐渐增大，从而引起岩石内部结构的致密程度下降，岩石的纵波波速逐渐的下降。随着冻融循环温度的降低，所形成的冻胀力对岩石孔隙和微裂缝的影响不断增大，岩石中可溶性矿物溶解和脱落的越多，致密程度减小，质量和纵波波速减小的越大；当试样冻融结束升温融化时，试样孔隙中的冰晶体会快速融化，此时岩石内部孔隙中会形成一个负压区域，由于压强作用外界水分会被吸入试样表面和孔隙中，此部分的质量随着冻融循环温度的降低不断增加，且脱落的质量大于从外界吸入水的质量，故随着冻融循环温度的降低，质量变化率整体上呈现下降趋势，纵波波速变化率整体上呈现上升趋势。

（3）不同冻融循环温度下岩样微观结构观察与分析

对自然状态和经过不同冻融循环温度处理后并自然晾干的砂岩进行表面微观结构观察，有助于从微观角度探究冻融损伤后砂岩的损伤机理。图 6为砂岩在自然状态下和经过冻融温度为-50℃循环80次并自然晾干后在扫描电子显微镜（SEM）下的细观图像，放大倍数为2k倍和5k倍。由图 6可以看出，经过冻融循环后砂岩的表观细观结构发生了一定的改变。在自然状态下砂岩的表面凹凸不平且表面颗粒都比较细，在扫描电子显微镜下棱角更加分明突出。而经过冻融循环处理的砂岩试块表面颗粒与自然状态比较，明显变得更加圆滑，棱角消失，且表面颗粒之间的差异感变得更加模糊，颗粒与颗粒之间的联系变得更为疏散。

图 6 自然状态下和冻融循环80次处理后砂岩的表面细观结构

Figure 6. Surface microstructures of sandstone in natural state and after 80 freeze-thaw cycles

下载: 全尺寸图片幻灯片

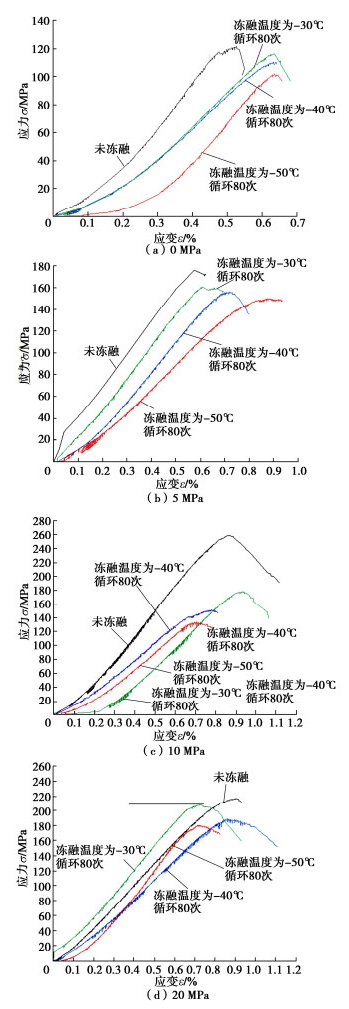
（4）冻融后砂岩三轴压缩应力-应变曲线

用TZW-3000II岩石真三轴流变试验机对冻融循环温度分别为20℃到-30℃、20℃到-40℃、20℃到-50℃和自然状态下的试件进行围压分别为0，5，10，20 MPa的常规三轴压缩试验。试验中沿轴向施加荷载，荷载施加速率为0.5 mm/min，加载采用轴向位移控制，直至试样破坏，而后停止加载，试验数据由仪器试验系统自动采集和存储。不同围压和不同冻融循环温度作用下砂岩的三轴压缩应力-应变曲线，如图 7所示。

图 7 不同围压和不同冻融温度作用下的应力-应变曲线

Figure 7. Stress-strain curves under different confining pressures and freeze-thaw temperatures

下载: 全尺寸图片幻灯片

从图 7中可以看出：砂岩岩样在冻融循环前后的应力–应变曲线形状大体上是相似的，均可分为压密、弹性变形、裂纹发展及破坏这4个阶段；砂岩的峰值强度随着冻融循环温度的降低不断下降，且冻融循环温度越低，弹性增长阶段曲线斜率越小；同时随着围压的增加，不同冻融循环温度处理后砂岩的峰值强度都有一定的增加，即围压增强效应。由于岩石形成过程的复杂性，致使岩石内部结构差异性较大，若岩石内部的软弱结构面较多，则会导致加载初期应变逐渐增加而压力却比较小、压密阶段延长的现象发生，如图 7（c）中冻融温度为-30℃的曲线。

3. 冻融细观损伤本构模型的建立

3.1 冻融损伤变量的选择

选择合适的损伤变量对岩石损伤理论的研究是至关重要的，损伤变量的选择可从宏观和微细观两个角度进行选择。以往的研究都是以宏观力学损伤理论为基础，通过宏观力学参数如弹性模量、波速等来表征岩石的损伤，而岩石的细观损伤才是岩石力学性能劣化的真正原因，对细观冻融损伤的定量化描述计算，其核心是选择损伤测量参数，由于经过冻融循环的砂岩试样，孔隙度的变化是岩样宏观力学性质变化的根本原因。因此，本文利用孔隙度来定义损伤变量，对岩石在不同冻融循环次数下的损伤程度进行反映，细观冻融损伤变量表达式为

${D_n} = 1 - \frac{{1 - {\phi _n}}}{{1 - {\phi _0}}} 。$

(3)

式中：D_n为岩石细观冻融损伤变量； ${\phi _n}$ 为冻融循环n次后岩石的孔隙率； ${\phi _0}$ 为岩石的初始孔隙率。

3.2 力损伤变量的确定

在外荷载作用下，定义损伤变量 ${D_q}$ 为某一应力水平q下已经破坏的微元数目n与初始状态下微元总数目N的比值，即

${D_q} = \frac{n}{N}。$

(4)

岩石受到外荷载作用时，其微元的破坏是随机发生的，根据Krajicinovic模型可知，损伤变量即为微元破坏概率P，若设微元破坏的概率密度函数为ϕ(x)，则P为F的累积分布函数，即

${D_q} = P = \int\limits_0^F {\phi (x){\text{d}}x} 。$

(5)

Weibull分布是一种较不保守的分布类型，它在一定程度上更真实地反映了随机变量的分布。鉴于此，本文基于岩石微元强度服从Weibull分布，其概率密度函数为

$\phi {\text{(}}F) = \frac{m}{{{F_0}}}{\left( {\frac{F}{{{F_0}}}} \right)^{m - 1}}\exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^m}} \right]。$

(6)

式中：F表示微元强度；m和F₀分别为Weibull分布的参数。

结合式（5），（6）得岩石在荷载作用下的损伤变量：

${D_q} = \int\limits_0^F {\phi (x){\text{d}}x} = 1 - \exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^m}} \right] 。$

(7)

3.3 冻融-荷载耦合作用下岩石的总损伤变量的确定

岩石在冻融和荷载共同作用下造成的损伤不是岩石在冻融和荷载作用下分别造成的损伤的简单叠加，是冻融和荷载作用的耦合而成的整体效应，这种整体效应会加剧岩石内部结构的损伤。设岩石在两种状态下的损伤用缺陷材料的体积来表示，即缺陷体积占材料总体积的比率，假设未损伤岩石、冻融损伤岩石和冻融-荷载耦合作用损伤后岩石的有效体积分别为V₀，V₁和V₂，则

${D_n} = 1 - \frac{{{V_1}}}{{{V_0}}}\text{，}$

(8)

${D_q} = 1 - \frac{{{V_2}}}{{{V_1}}}。$

(9)

联立式（8），（9）可得冻融-荷载耦合作用下的岩石总损伤变量：

${D_{\text{S}}} = {D_n} + {D_q} - {D_n}{D_q} 。$

(10)

式中： ${D_{\text{S}}}$ 为冻融-荷载耦合作用下的岩石总损伤变量。

将式（3），（7）代入式（10）可得岩石在冻融-荷载耦合作用下的总损伤变量：

${D_{\text{S}}} = 1 - \frac{{1 - {\phi _n}}}{{1 - {\phi _0}}}\exp \left[ { - {{\left( {\frac{F}{{{F_0}}}} \right)}^m}} \right]。$

(11)

3.4 围压作用下岩石微元强度的确定

Matsuoka等^[14]于1974年提出了SMP强度准则。即，材料所受到的剪应力与正应力的比值达到某一数值时发生破坏。SMP准则有更强的物理推导过程，各变量物理意义明确，同时又克服了Mohr-Coulomb准则中未考虑中主应力对岩石强度影响的缺陷，该准则对某些岩石类材料的适用性是比较理想的。其表达式为

${I_1}{I_2}{\text{/}}{I_3} = K = 8{\tan ^2}\varphi {\text{ + }}9 。$

(12)

式中：I₁，I₂和I₃分别为应力张量第一不变量、应力张量第二不变量和应力张量第三不变量；φ为岩石的内摩擦角；K为材料常数；并且I₁，I₂和I₃分别为

${I_1} = \sigma _1^* + \sigma _2^* + \sigma _3^*\text{，}$

(13)

${I_2} = \sigma _1^*\sigma _2^* + \sigma _2^*\sigma _3^* + \sigma _1^*\sigma _3^*\text{，}$

(14)

${I_3} = \sigma _1^*\sigma _2^*\sigma _3^* 。$

(15)

式中： $\sigma _1^*$ ， $\sigma _2^*$ 和 $\sigma _3^*$ 分别为最大、中间和最小主应力。

以上SMP准则的公式只适用于摩擦性材料而不适用于c-φ材料，Satake^[15]、Mastuoka等^[16]拓展了该准则，使其同时适应非黏结性材料和黏结性材料，并提出黏结应力 ${\sigma _0}$ ，其表达式为

${\sigma _0} = c\cot \varphi 。$

(16)

式中：c为材料的黏聚力。

修改的SMP准则表达式为

${\hat I_1}{\hat I_2}/{\hat I_3} = K = 8{\tan ^2}\varphi {\text{ + }}9 。$

(17)

式中：

$\left. { \begin{array}{l}{\widehat{I}}_{1}={\sigma }_{1}^{\text{*}}\text{+}{\sigma }_{2}^{\text{*}}\text{+}{\sigma }_{3}^{\text{*}}\text{+}3{\sigma }_{0}\text{ }\text{，}\\ {\widehat{I}}_{2}=\text{(}{\sigma }_{1}^{\text{*}}\text{+}{\sigma }_{0}\text{)}({\sigma }_{2}^{\text{*}}\text{+}{\sigma }_{0})\text{+}({\sigma }_{2}^{\text{*}}\text{+}{\sigma }_{0})({\sigma }_{3}^{\text{*}}\text{+}{\sigma }_{0})+\\ \;\;\;\;\;\;\;\; \text{ }({\sigma }_{3}^{\text{*}}\text{+}{\sigma }_{0})({\sigma }_{1}^{\text{*}}\text{+}{\sigma }_{0})\text{ }\text{，}\\ {\widehat{I}}_{3}=\text{(}{\sigma }_{1}^{\text{*}}\text{+}{\sigma }_{0}\text{)}({\sigma }_{2}^{\text{*}}\text{+}{\sigma }_{0})({\sigma }_{3}^{\text{*}}\text{+}{\sigma }_{0})\text{ }。\end{array} } \right\}$

(18)

将式（17），（18）联立，并根据相关联流动法则可得黏性材料的SMP准则的表达式：

$\frac{{\sigma }_{1}^{\text{*}}\text{+}{\sigma }_{0}}{{\sigma }_{3}^{\text{*}}\text{+}{\sigma }_{0}}\text{=}\frac{1}{4}{\left(\sqrt{8{\mathrm{tan}}^{2}\varphi \text{+}9}\text{+}\sqrt{8{\mathrm{tan}}^{2}\varphi \text{+6}-\text{2}\sqrt{8{\mathrm{tan}}^{2}\varphi \text{+}9}}-1\right)}^{2}。$

(19)

依据式（19）可得基于SMP准则下的岩石微元强度F：

$F=f({\sigma }_{1}\text{，}{\sigma }_{2}\text{，}{\sigma }_{3})=\frac{{\sigma }_{1}^{\text{*}}\text{+}{\sigma }_{0}}{{\sigma }_{3}^{\text{*}}\text{+}{\sigma }_{0}} 。$

(20)

根据广义胡克定律和应变等价原理，且 ${\sigma _2} = {\sigma _3}$ ，将式（20）中的有效应力换成名义应力表示，可得基于SMP准则岩石在围压作用下的微元强度F，即

$F = \frac{{E{\varepsilon _1} + 2\mu {\sigma _3} + {\sigma _0}}}{{{\sigma _3} + {\sigma _0}}} 。$

(21)

3.5 冻融与荷载耦合作用下的损伤演化方程

将式（21）代入式（11）可得

${D_{\text{S}}} = 1 - \frac{{1 - {\phi _n}}}{{1 - {\phi _0}}}\exp \left[ { - {{\left( {\frac{{{E_n}{\varepsilon _1} + 2\mu {\sigma _3} + {\sigma _0}}}{{{F_0}({\sigma _3} + {\sigma _0})}}} \right)}^m}} \right] 。$

(22)

3.6 岩石在冻融与围压耦合作用下的三轴损伤本构模型

根据Lemaitre应变等价性假设原理和有效应力原理，则可建立岩石损伤本构关系如下：

$\sigma _i^* = \frac{{{\sigma _i}}}{{1 - D}}{\text{ (}}i = 1,2,3)。$

(23)

式中： $\sigma _i^*$ 为岩石的有效应力； $\sigma _i^{}$ 为岩石的名义应力（试验测得的应力）；D为岩石的总损伤变量。

由广义胡克定律可知

$\varepsilon _i^* = \left[ {\sigma _i^* - v(\sigma _j^* + \sigma _k^*)} \right]/{E_n}。$

(24)

式中：i，j，k分别为1，2，3；E_n为岩石冻融循环n次后的弹性模量； $\nu$ 为泊松比； $\varepsilon _i^*$ 为与有效应力 $\sigma _i^*$ 所对应的有效应变。

根据变形协调条件得

$\varepsilon _i^*{\text{ = }}\varepsilon _i^{}。$

(25)

则由式（23）~（25）可得岩石损伤本构关系:

${\sigma _1} = {E_n}{\varepsilon _1}{\text{(}}1 - D{\text{)}} + v({\sigma _2} + {\sigma _3})。$

(26)

岩石实际受到的轴向应力 ${\sigma _1}$ 为试验中测量的轴向偏应力 ${\sigma _{1{\text{t}}}}$ 和围压 ${\sigma _3}$ 之和，即

${\sigma _1} = {\sigma _{1{\text{t}}}} + {\sigma _3}。$

(27)

在围压作用下，岩石产生的初始轴向应变为

${\varepsilon _{10}} = \frac{{1 - 2v}}{{{E_n}}}\sigma {}_3 。$

(28)

岩石实际产生的轴向应变 ${\varepsilon _1}$ 为试验中测量的轴向应变 ${\varepsilon _{1{\text{t}}}}$ 与初始产生的轴向应变 ${\varepsilon _{10}}$ 之和，即

${\varepsilon _1} = {\varepsilon _{1{\text{t}}}}{\text{ + }}{\varepsilon _{10}}。$

(29)

将式（22）和（27）~（29）代入式（26）中可得冻融-荷载耦合作用下岩石三轴压缩过程中损伤统计本构模型

${\sigma _{1{\text{t}}}} = \left[ {{E_n}{\varepsilon _{1{\text{t}}}} + (1 - 2v){\sigma _3}} \right]\frac{{1 - {\phi _n}}}{{1 - {\phi _0}}} \cdot \\ \;\;\;\;\;\; \exp \left[ { - {{\left( {\frac{{{E_n}{\varepsilon _{1{\text{t}}}} + {\sigma _3} + {\sigma _0}}}{{{F_0}({\sigma _3} + {\sigma _0})}}} \right)}^m}} \right] + (2v - 1){\sigma _3} 。$

(30)

4. 模型参数的确定

从上述模型可以看出，该模型中需要确定的参数有ϕ_n和m，F₀。

4.1 不同冻融循环次数下岩石的损伤本构模型参数确定

本文通过孔隙率随冻融循环次数的变化来表征岩石在不同冻融循环次数作用下的损伤程度，即D_n。对于参数ϕ_n可通过岩石核磁共振试验来确定。

4.2 不同围压作用下岩石的损伤本构模型参数确定

对于参数m和F₀可采用岩石应力应变曲线的峰值点（ ${\varepsilon _{\text{p}}}$ ， ${\sigma _{\text{p}}}$ ）来确定，即极值法。具体求解过程如下。

峰值应力 ${\sigma _{\text{p}}}$ 与所对应的峰值应变 ${\varepsilon _{\text{p}}}$ 满足下列两个几何条件

$\varepsilon ={\varepsilon }_{\text{p}}\text{，}{\sigma }_{1}={\sigma }_{\text{p}} \text{，}$

(31)

$\varepsilon ={\varepsilon }_{\text{p}}\text{，}\text{ }\frac{\text{d}{\sigma }_{1}}{\text{d}{\varepsilon }_{1}}=0 。$

(32)

将式（31），（32）代入式（30）中，可得到两个关于Weibull分布参数m和F₀的关系式，并最终求出模型参数m和F₀。

首先将式（31）代入式（30）中可得

$\frac{{1 - {\phi _n}}}{{1 - {\phi _0}}}\exp \left[ { - {{\left( {\frac{{{F_{{\text{sc}}}}}}{{{F_0}}}} \right)}^m}} \right] = \frac{{{\sigma _{\text{p}}} + (1 - 2v){\sigma _3}}}{{{E_n}{\varepsilon _{\text{p}}} + (1 - 2v){\sigma _3}}} \text{，}$

(33)

其中，

$F{\text{ = }}\frac{{{E_n}{\varepsilon _{1{\text{t}}}} + {\sigma _3} + {\sigma _0}}}{{({\sigma _3} + {\sigma _0})}} 。$

(34)

式（33）中F_SC为应力应变曲线极值点对应的F，即F_SC为式（34）中 ${\varepsilon _{1{\text{t}}}}$ 和 ${\sigma _{1{\text{t}}}}$ 满足式（31）条件时的F值。

其次再对式（30）进行求导，并结合式（31）即可。对式（30）求取偏微分得

$\left.\frac{\partial \sigma_{1 \mathrm{t}}}{\partial \varepsilon_{1 \mathrm{t}}}\right|_{\substack{\sigma_{1\mathrm{t}}=\sigma_{\mathrm{p}} \\ \varepsilon_{1\mathrm{t}}=\varepsilon_{\mathrm{p}}}}=\frac{1-\phi_n}{1-\phi_0} \exp \left[-\left(\frac{F}{F_0}\right)^m\right] . \\ \;\;\;\; \left\{ {{E_n} - \frac{{m\left[ {{E_n}{\varepsilon _{\text{p}}} + (1 - 2v){\sigma _3}} \right]}}{{{F_{{\text{sc}}}}}}{{\left( {\frac{{{F_{{\text{sc}}}}}}{{{F_0}}}} \right)}^m}\frac{{\partial {F_{{\text{sc}}}}}}{{\partial {\varepsilon _{1{\text{t}}}}}}} \right\} 。$

(35)

由式（32）知

${E_n} - \frac{{m\left[ {{E_n}{\varepsilon _{\text{p}}} + (1 - 2v){\sigma _3}} \right]}}{{{F_{{\text{sc}}}}}}{\left( {\frac{{{F_{{\text{sc}}}}}}{{{F_0}}}} \right)^m}\frac{{\partial {F_{{\text{sc}}}}}}{{\partial {\varepsilon _{1{\text{t}}}}}}{\text{ = }}0 。$

(36)

再对式（34）求取偏微分得

$\left.\frac{\partial F_{\mathrm{sc}}}{\partial \varepsilon_{1 \mathrm{t}}}\right|_{\substack{\sigma_{1 \mathrm{t}}=\sigma_{\mathrm{p}} \\ \varepsilon_{1\mathrm{t}}=\varepsilon_{\mathrm{p}}}}=\frac{E_n}{\left(\sigma_3+\sigma_0\right)} 。$

(37)

把式（37）代入式（36）可得

${\left( {\frac{{{F_{{\text{sc}}}}}}{{{F_0}}}} \right)^m}{\text{ = }}\frac{{{F_{{\text{sc}}}}\left( {{\sigma _3} + {\sigma _0}} \right)}}{{m\left[ {{E_n}{\varepsilon _{\text{p}}} + (1 - 2v){\sigma _3}} \right]}}{\text{ = }}\frac{{{E_n}{\varepsilon _{\text{p}}} + {\sigma _3} + {\sigma _0}}}{{m\left[ {{E_n}{\varepsilon _{\text{p}}} + (1 - 2v){\sigma _3}} \right]}} 。$

(38)

对比式（33）可得参数m和F₀的表达式为

$m=\frac{1}{\mathrm{ln}\frac{1-{\phi }_{n}}{1-{\phi }_{0}}\left[\frac{{E}_{n}{\varepsilon }_{\text{p}}+(1-2v){\sigma }_{3}}{{\sigma }_{\text{p}}+(1-2v){\sigma }_{3}}\right]}\frac{{E}_{n}{\varepsilon }_{\text{p}}+{\sigma }_{3}+{\sigma }_{0}}{\left[{E}_{n}{\varepsilon }_{\text{p}}+(1-2v){\sigma }_{3}\right]}\text{，}$

(39)

${F_0} = \frac{{{E_n}{\varepsilon _{\text{p}}} + {\sigma _3} + {\sigma _0}}}{{({\sigma _3} + {\sigma _0})}}{\left( {\frac{{{E_n}{\varepsilon _{\text{p}}} + (1 - 2v){\sigma _3}}}{{{E_n}{\varepsilon _{\text{p}}} + {\sigma _3} + {\sigma _0}}}m} \right)^{\frac{1}{m}}} 。$

(40)

按照上述的参数确定方法，将得到的参数ϕ_n和m，F₀代入式（30）中，即可得到岩石在冻融-荷载耦合作用下的细观损伤本构模型。

5. 冻融-围压耦合作用下岩石的损伤本构模型验证

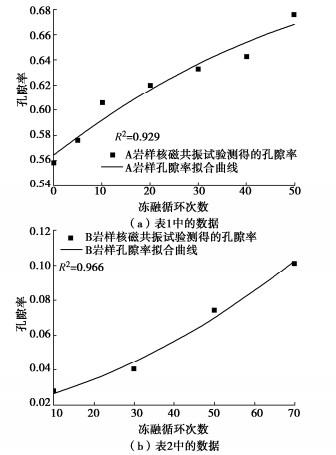
为验证本文建立的岩石损伤演化方程、细观损伤本构模型及参数确定方法的合理性及准确性，本文作者首先通过引用张二峰等^[17]冻融循环作用下砂岩细观损伤演化规律试验研究和许玉娟等^[18]冻融岩石核磁共振检测及冻融损伤机制分析的的相关研究成果来获得核磁共振试验下测得的岩样孔隙率，并且通过拟合孔隙率随着冻融循环次数的变化关系，得到不同冻融循环次数后岩样的核磁共振孔隙率ϕ_n与冻融次数n的拟合方程。最后采用张蒙军^[19]冻融环境下红砂岩物理力学特性试验的相关研究成果来进行验证。

张二峰等^[17]冻融循环作用下砂岩细观损伤演化规律试验研究中岩样的核磁共振孔隙率见表 1。

表 1 不同冻融循环次数下岩样的核磁共振孔隙率

Table 1. NMR porosities of rock samples under different freeze-thaw cycles

冻融循环次数	0	5	10	20	30	40	50
孔隙率ϕ_n/%	5.58	5.76	6.06	6.20	6.33	6.43	6.76

下载: 导出CSV

| 显示表格

许玉娟^[18]冻融岩石核磁共振检测及冻融损伤机制分析的研究中岩样的核磁共振孔隙率见表 2。

表 2 岩样的核磁共振孔隙率

Table 2. NMR porosities of rock samples

冻融循环次数	10	30	50	70
孔隙率ϕ_n/%	2.83	4.09	7.43	10.13

下载: 导出CSV

| 显示表格

用二次多项式分别对表 1和表 2中不同冻融循环次数作用下岩样的核磁共振孔隙率进行拟合，拟合曲线如图 8所示。

图 8 孔隙率随冻融循环次数的拟合曲线

Figure 8. Fitting curves of porosity with number of freeze-thaw cycles

下载: 全尺寸图片幻灯片

由图 8可知，用2次多项式拟合表 1和表 2中岩样的核磁共振孔隙率随冻融循环次数变化的曲线拟合优度（R²）分别为0.929，0.966，表明用表 2中的不同冻融循环次数作用下岩样的核磁共振孔隙率得到的拟合曲线较表 1的拟合曲线的拟合程度高，故用表 2中岩样的核磁共振孔隙率随冻融循环次数变化的数据进行拟合得到的参数a，b和c进行计算较为准确。

则核磁共振孔隙率ϕ_n与冻融循环次数n的拟合方程为

${\phi _n}{\text{ = 9}} \times {10^{{\text{ - 6}}}}{n^2}{\text{ + }}0.00054n{\text{ + }}0.02062 。$

(41)

则可得到冻融循环次数为0，5，10，20和40次后岩石的孔隙率拟合值，见表 3。

表 3 不同冻融循环次数作用下岩样的核磁共振孔隙率拟合值

Table 3. Fitting values of NMR porosity of rock samples under different freeze-thaw cycles

冻融循环次数	0	5	10	20	40
孔隙率拟合值/%	2.062	2.355	2.83	3.502	5.662

下载: 导出CSV

| 显示表格

张蒙军^[19]冻融环境下红砂岩物理力学特性试验的相关研究成果中，首先对红砂岩进行不同冻融循环次数的冻融试验（循环次数分别为0，5，10，20和40次）。其次，再对冻融循环后的岩石进行4种围压下的常规三轴压缩试验（围压分别为0，2，4，6 MPa）得到试验曲线。最后再把试验曲线与模型理论曲线进行对比，来验证该模型的合理性及准确性。不同冻融循环次数和不同围压下红砂岩的力学参数见参考文献[19]。

将表 3中岩样的核磁共振孔隙率拟合值和原始物理力学参数代入式（39），（40），可得不同冻融循环次数和不同围压作用下的Weibull分布参数m和F₀，见表 4。

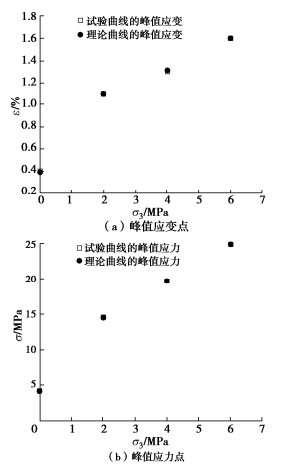
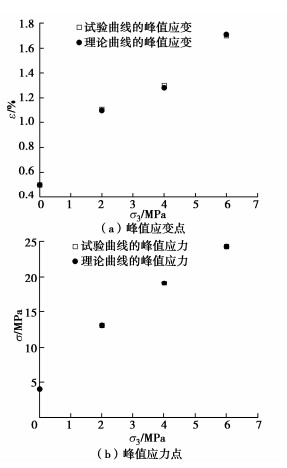
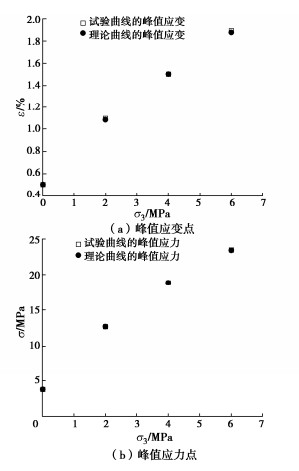
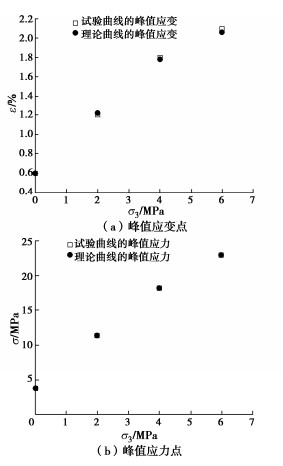
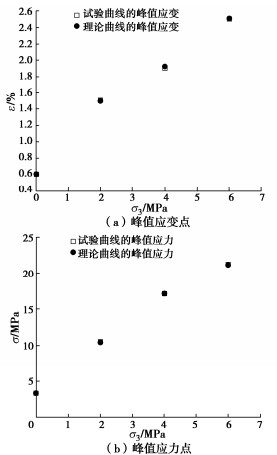
表 4 不同冻融循环次数和不同围压下红砂岩模型计算参数表

Table 4. Model parameters of red sandstone under different freeze-thaw cycles and confining pressures

冻融次数	σ₃/MPa	σ_p /MPa	ε_p /%	m	F₀/MPa
0	0	4.230	0.4	4.634	1.987
	2	14.572	1.1	6.869	3.369
	4	19.652	1.3	17.460	3.383
	6	24.866	1.6	25.257	3.406
5	0	4.020	0.5	3.127	1.653
	2	13.101	1.1	6.556	3.120
	4	19.132	1.3	13.958	3.113
	6	24.347	1.7	10.828	3.607
10	0	3.800	0.5	3.225	1.651
	2	12.701	1.1	4.287	3.124
	4	18.910	1.5	5.562	3.602
	6	23.519	1.9	5.116	3.880
20	0	3.749	0.6	3.007	1.466
	2	11.356	1.2	2.701	2.678
	4	18.100	1.8	2.887	3.591
	6	22.903	2.1	3.499	4.031
40	0	3.301	0.6	1.286	0.836
	2	10.570	1.5	1.408	2.197
	4	17.121	1.9	2.367	3.492
	6	21.274	2.5	2.121	3.722

下载: 导出CSV

| 显示表格

将试验所得的不同冻融循环次数和不同围压作用下的应力-应变曲线峰值点与模型理论曲线峰值点进行对比，如图 9~13所示。发现两者吻合度较好，表明已建立的包含岩石冻融-围压耦合损伤演化方程的细观损伤本构模型能够较好地反映岩石三轴压缩过程的应力-应变峰值特性。

图 9 冻融循环0次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 9. Peak points of experimental and theoretical curves under different confining pressures after 0 freeze-thaw cycle

下载: 全尺寸图片幻灯片

图 10 冻融循环5次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 10. Peak points of experimental and theoretical curves under different confining pressures after 5 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 11 冻融循环10次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 11. Peak points of experimental and theoretical curves under different confining pressures after 10 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 12 冻融循环20次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 12. Peak points of experimental and theoretical curves under different confining pressures after 20 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 13 冻融循环40次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 13. Peak points of experimental and theoretical curves under different confining pressures after 40 freeze-thaw cycles

下载: 全尺寸图片幻灯片

从图 9~13可知：在同一围压下，随着冻融循环次数的增加，红砂岩的峰值应力逐渐降低；在同一冻融循环次数下，随着围压的增加，红砂岩的峰值应力和峰值应变逐渐增大，与试验结果一致；理论曲线可以反映岩石强度和变形随冻融循环次数和围压变化的趋势，同时也表明本文建立的包含岩石冻融-围压耦合损伤演化方程的细观损伤本构模型能够充分地反映冻融岩石强度依赖于围压的特征。

6. 结论

本文首先通过进行室内冻融循环试验、扫描电子显微镜观测和三轴压缩试验对砂岩质量损失、微观结构、力学特性以及冻融损伤机理进行了研究与分析。其次，采用损伤力学理论，引入能够反映岩石在冻融循环破坏过程中的细观冻融损伤变量和力损伤变量，推导了冻融与围压耦合作用下岩石的总损伤变量。同时，假定岩石微元强度服从Weibull分布，选取SMP准则，并基于Lemaitre应变等价性假设建立了包含岩石冻融-围压耦合损伤演化方程的细观损伤本构模型来研究岩石破坏过程中的损伤特性。

（1）不同冻融循环温度处理前后砂岩岩样的质量变化均呈现下降的趋势，随着冻融循环温度的降低，质量变化率整体上呈现下降趋势。不同冻融循环温度处理前后砂岩岩样的纵波波速变化均呈现下降的趋势，随着冻融循环温度的下降，纵波波速变化率整体上呈现上升趋势。

（2）试验所用砂岩在冻融循环处理后发生了劣化，并且随着冻融循环温度的下降劣化程度加剧。经过冻融循环处理的砂岩试块表面颗粒与自然状态比较，变得更加圆滑，棱角明显消失，且颗粒与颗粒之间的联系更加模糊与紧密，这种改变效果随着冻融循环温度的下降更加明显；若岩石内部的软弱结构面较多，则会导致加载初期应变逐渐增加而压力却比较小、压密阶段延长的现象发生。

（3）本文建立的岩石细观损伤本构模型理论曲线峰值点与试验曲线峰值点吻合度较好，表明该细观损伤本构模型能够较好地反映三轴压缩过程中岩石的应力-应变峰值特性，对寒区工程中岩土体工程建设具有一定的现实意义。

（4）本文建立的细观损伤本构模型理论曲线峰值点与试验曲线峰值点的峰值应变随冻融循环次数的变化有一定的波动，而峰值应力随着冻融循环次数的变化是不大的，总体而言理论曲线峰值点与试验曲线峰值点随着冻融循环次数的变化吻合度较好。

（5）本文建立的细观损伤本构模型中，模型参数F₀有明显的力学意义，在一定程度上与岩石峰值应力有关，峰值应力增加，F₀的值也逐渐增大，且随着围压的不断增大，F₀的值也不断增大。

（6）本文建立的细观损伤本构模型没有特定的岩石种类参数，模型所需参数均可通过实验室常规三轴压缩试验获得，与岩石的种类无关，可适用于各类岩石，工程应用方便，具有适用性广的特点。

图 1 砂岩冻融试验试块

Figure 1. Freeze-thaw test block of sandstone

下载: 全尺寸图片幻灯片

图 2 TZW-3000II岩石真三轴流变试验机

Figure 2. TZW-3000II rock true triaxial rheological testing machine

下载: 全尺寸图片幻灯片

图 3 WGD-501立式冻融机

Figure 3. WGD-501 vertical freeze-thaw machine

下载: 全尺寸图片幻灯片

图 4 质量变化率随冻融循环温度变化关系曲线

Figure 4. Variation of mass change rate with temperature of freeze-thaw cycle

下载: 全尺寸图片幻灯片

图 5 纵波波速变化率随冻融循环温度变化关系曲线

Figure 5. Variation of change rate of longitudinal wave velocity with temperature of freeze-thaw cycle

下载: 全尺寸图片幻灯片

图 6 自然状态下和冻融循环80次处理后砂岩的表面细观结构

Figure 6. Surface microstructures of sandstone in natural state and after 80 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 7 不同围压和不同冻融温度作用下的应力-应变曲线

Figure 7. Stress-strain curves under different confining pressures and freeze-thaw temperatures

下载: 全尺寸图片幻灯片

图 8 孔隙率随冻融循环次数的拟合曲线

Figure 8. Fitting curves of porosity with number of freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 9 冻融循环0次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 9. Peak points of experimental and theoretical curves under different confining pressures after 0 freeze-thaw cycle

下载: 全尺寸图片幻灯片

图 10 冻融循环5次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 10. Peak points of experimental and theoretical curves under different confining pressures after 5 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 11 冻融循环10次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 11. Peak points of experimental and theoretical curves under different confining pressures after 10 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 12 冻融循环20次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 12. Peak points of experimental and theoretical curves under different confining pressures after 20 freeze-thaw cycles

下载: 全尺寸图片幻灯片

图 13 冻融循环40次时不同围压作用下试验曲线和理论曲线的峰值点图

Figure 13. Peak points of experimental and theoretical curves under different confining pressures after 40 freeze-thaw cycles

下载: 全尺寸图片幻灯片

表 1 不同冻融循环次数下岩样的核磁共振孔隙率

Table 1 NMR porosities of rock samples under different freeze-thaw cycles

冻融循环次数	0	5	10	20	30	40	50
孔隙率ϕ_n/%	5.58	5.76	6.06	6.20	6.33	6.43	6.76

下载: 导出CSV

表 2 岩样的核磁共振孔隙率

Table 2 NMR porosities of rock samples

冻融循环次数	10	30	50	70
孔隙率ϕ_n/%	2.83	4.09	7.43	10.13

下载: 导出CSV

表 3 不同冻融循环次数作用下岩样的核磁共振孔隙率拟合值

Table 3 Fitting values of NMR porosity of rock samples under different freeze-thaw cycles

冻融循环次数	0	5	10	20	40
孔隙率拟合值/%	2.062	2.355	2.83	3.502	5.662

下载: 导出CSV

表 4 不同冻融循环次数和不同围压下红砂岩模型计算参数表

Table 4 Model parameters of red sandstone under different freeze-thaw cycles and confining pressures

冻融次数	σ₃/MPa	σ_p /MPa	ε_p /%	m	F₀/MPa
0	0	4.230	0.4	4.634	1.987
	2	14.572	1.1	6.869	3.369
	4	19.652	1.3	17.460	3.383
	6	24.866	1.6	25.257	3.406
5	0	4.020	0.5	3.127	1.653
	2	13.101	1.1	6.556	3.120
	4	19.132	1.3	13.958	3.113
	6	24.347	1.7	10.828	3.607
10	0	3.800	0.5	3.225	1.651
	2	12.701	1.1	4.287	3.124
	4	18.910	1.5	5.562	3.602
	6	23.519	1.9	5.116	3.880
20	0	3.749	0.6	3.007	1.466
	2	11.356	1.2	2.701	2.678
	4	18.100	1.8	2.887	3.591
	6	22.903	2.1	3.499	4.031
40	0	3.301	0.6	1.286	0.836
	2	10.570	1.5	1.408	2.197
	4	17.121	1.9	2.367	3.492
	6	21.274	2.5	2.121	3.722

下载: 导出CSV

参考文献(19)

[1]	汤连生, 张鹏程, 王思敬. 水-岩化学作用的岩石宏观力学效应的试验研究[J]. 岩石力学与工程学报, 2002, 21(4): 526-531. doi: 10.3321/j.issn:1000-6915.2002.04.015 TANG Liansheng, ZHANG Pengcheng, WANG Sijing. Testing study on macroscopic mechanics effect of chemical action of water on rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(4): 526-531. (in Chinese) doi: 10.3321/j.issn:1000-6915.2002.04.015
[2]	WIEDERHORN S M. A chemical interpretation of static fatigue[J]. Journal of the American Ceramic Society, 1972, 55(2): 81-85. doi: 10.1111/j.1151-2916.1972.tb11215.x
[3]	霍润科, 李宁, 刘汉东. 酸性环境下类砂岩材料波速特性分析[J]. 岩土力学, 2005, 26(4): 608-611. doi: 10.3969/j.issn.1000-7598.2005.04.021 HUO Runke, LI Ning, LIU Handong. Analysis of characteristics of longitudinal wave velocity of mortar subjected to hydrochloric acid attack[J]. Rock and Soil Mechanics, 2005, 26(4): 608-611. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.04.021
[4]	丁梧秀, 冯夏庭. 化学腐蚀下灰岩力学效应的试验研究[J]. 岩石力学与工程学报, 2004, 23(21): 3571-3576. doi: 10.3321/j.issn:1000-6915.2004.21.002 DING Wuxiu, FENG Xiating. Testing study on mechanical effect for limestone under chemical erosion[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(21): 3571-3576. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.21.002
[5]	杨更社, 蒲毅彬, 马巍. 寒区冻融环境条件下岩石损伤扩展研究探讨[J]. 实验力学, 2002, 17(2): 220-226. doi: 10.3969/j.issn.1001-4888.2002.02.015 YANG Gengshe, PU Yibin, MA Wei. Discussion on the damage propagation for the rock under the frost and thaw condition of frigid zone[J]. Journal of Experimental Mechanics, 2002, 17(2): 220-226. (in Chinese) doi: 10.3969/j.issn.1001-4888.2002.02.015
[6]	何国梁, 张磊, 吴刚. 循环冻融条件下岩石物理特性的试验研究[J]. 岩土力学, 2004, 25(增刊2): 52-56. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2004S200A.htm HE Guoliang, ZHANG Lei, WU Gang. Test study on physical characteristics of rock under freezing-thawing cycles[J]. Rock and Soil Mechanics, 2004, 25(S2): 52-56. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2004S200A.htm
[7]	陈有亮, 王朋, 张学伟, 等. 花岗岩在化学溶蚀和冻融循环后的力学性能试验研究[J]. 岩土工程学报, 2014, 36(12): 2226-2235. doi: 10.11779/CJGE201412010 CHEN Youliang, WANG Peng, ZHANG Xuewei, et al. Experimental research on mechanical properties of granite in chemical dissolution under freeze-thaw cycles[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(12): 2226-2235. (in Chinese) doi: 10.11779/CJGE201412010
[8]	韩铁林, 师俊平, 陈蕴生, 等. 不同化学腐蚀下砂岩冻融力学特性劣化的试验研究[J]. 固体力学学报, 2017, 38(6): 503-520. https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX201706003.htm HAN Tielin, SHI Junping, CHEN Hengchen, et al. Laboratory investigation on the mechanical properties of sandstone immersed in different chemical corrosion under freeze-thaw cycles[J]. Chinese Journal of Solid Mechanics, 2017, 38(6): 503-520. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GTLX201706003.htm
[9]	张君岳, 田镇, 刘桓兑, 等. 冻融红砂岩物理力学性质损伤演化试验研究[J]. 矿业研究与开发, 2020, 40(10): 79-84. https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202010015.htm ZHANG Junyue, TIAN Zhen, LIU Huandui, et al. Experimental research of physical and mechanical damage evolution of freeze-thaw red sandstone[J]. Mining Research and Development, 2020, 40(10): 79-84. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KYYK202010015.htm
[10]	张慧梅, 杨更社. 冻融与荷载耦合作用下岩石损伤模型的研究[J]. 岩石力学与工程学报, 2010, 29(3): 471-476. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201003007.htm ZHANG Huimei, YANG Gengshe. Research on damage model of rock under coupling action of freeze-thaw and load[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(3): 471-476. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201003007.htm
[11]	徐光苗, 刘泉声. 岩石冻融破坏机理分析及冻融力学试验研究[J]. 岩石力学与工程学报, 2005, 24(17): 3076-3082. doi: 10.3321/j.issn:1000-6915.2005.17.012 XU Guangmiao, LIU Quansheng. Analysis of mechanism of rock failure due to freeze-thaw cycling and mechanical testing study on frozen-thawed rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3076-3082. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.17.012
[12]	孟祥振, 张慧梅, 康晓革. 含孔隙冻融岩石的损伤本构模型[J]. 西安科技大学学报, 2019, 39(4): 688-692. https://www.cnki.com.cn/Article/CJFDTOTAL-XKXB201904019.htm MENG Xiangzhen, ZHANG Huimei, KANG Xiaoge. Damage constitutive model of porous rock under freeze-thaw[J]. Journal of Xi'an University of Science and Technology, 2019, 39(4): 688-692. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XKXB201904019.htm
[13]	杨涛, 霍树义, 金坎辉, 等. 冻融循环下砂岩损伤演化及本构模型[J]. 地质与勘探, 2020, 56(4): 826-831. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKT202004016.htm YANG Tao, HUO Shuyi, JIN Kanhui, et al. Damage evolution and constitutive model under freeze-thaw cycles[J]. Geology and Exploration, 2020, 56(4): 826-831. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZKT202004016.htm
[14]	MATSUOKA H, NAKAI T R. Stress-deformation and strength characteristics of soil under three different principal stresses[J]. Proceedings of the Japan Society of Civil Engineers, 1974(232): 59-70.
[15]	SATAKE M. Stress-deformation and strength characteristics of soil under three difference principle stresses[J]. Proc of Japan Society of Civil Engineers, 1976, 246: 137-138.
[16]	MATSUOKA H, HOSHIKAWA T, UENO K. A general failure criterion and stress-strain relation for granular materials to metals[J]. Soils and Foundations, 1990, 30(2): 119-127.
[17]	张二锋, 杨更社, 刘慧. 冻融循环作用下砂岩细观损伤演化规律试验研究[J]. 煤炭工程, 2018, 50(10): 50-55. https://www.cnki.com.cn/Article/CJFDTOTAL-MKSJ201810013.htm ZHANG Erfeng, YANG Gengshe, LIU Hui. Experimental study on meso-damage evolution of sandstone under freeze-thaw cycles[J]. Coal Engineering, 2018, 50(10): 50-55. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MKSJ201810013.htm
[18]	许玉娟, 周科平, 李杰林, 等. 冻融岩石核磁共振检测及冻融损伤机制分析[J]. 岩土力学, 2012, 33(10): 3001-3005, 3102. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201210022.htm XU Yujuan, ZHOU Keping, LI Jielin, et al. Study of rock NMR experiment and damage mechanism analysis under freeze-thaw condition[J]. Rock and Soil Mechanics, 2012, 33(10): 3001-3005, 3102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201210022.htm
[19]	张蒙军. 冻融环境下红砂岩物理力学特性试验研究[D]. 西安: 西安科技大学, 2015. ZHANG Mengjun. The Experimental Studyon the Physical and Mechanical Properties of Red Sandstone under the Environment of Freeze-Thaw Environment[D]. Xi'an: Xi'an University of Science and Technology, 2015. (in Chinese)

施引文献(38)

期刊类型引用(17)

1.	侯召旭，刘先峰，王通，张俊，袁胜洋，胡金山. 冻融损伤石英岩力学特性及损伤本构模型. 长江科学院院报. 2025(01): 177-185 . 百度学术
2.	王文通，郭沙，李治兴，李治国，刘传举. 基于核磁共振技术的砂岩孔隙结构冻融损伤演化规律试验研究. 黄金科学技术. 2025(01): 114-126 . 百度学术
3.	刘先峰，王通，李建国，袁胜洋，侯召旭，张俊. 冻融循环作用下灰岩和石英岩力学特性及损伤本构模型试验研究. 中国铁道科学. 2025(01): 1-14 . 百度学术
4.	邓乃夫，乔兰，刘建，张庆龙，李庆文. 基于裂隙演化微分动力学机制的岩石损伤本构模型. 中南大学学报(自然科学版). 2024(02): 677-689 . 百度学术
5.	秦飞飞，盛冬发. 冻融循环下混杂纤维再生混凝土抗压强度预测方法. 科学技术与工程. 2024(16): 6870-6881 . 百度学术
6.	孙大增，赵文，许兴亮，王鑫. 不同组构砂岩微观破坏特征分析. 东北大学学报(自然科学版). 2024(04): 584-591 . 百度学术
7.	王磊，陈礼鹏，谢广祥，范浩，李少波，邹鹏，张宇. CO_2-荷载耦合作用下煤体细观统计损伤本构模型及验证. 煤炭学报. 2024(06): 2630-2642 . 百度学术
8.	张昊，苏占东，孙进忠，牛耀，梁金平，张建勇，王鸷文. 冻融温度区间对砂岩声发射特性的影响. 科学技术与工程. 2024(18): 7812-7820 . 百度学术
9.	张蓉蓉，沈永辉，马冬冬，平琦，杨毅. 循环冲击作用下冻融红砂岩动力学特性与损伤机理. 爆炸与冲击. 2024(08): 133-148 . 百度学术
10.	张俊，刘先峰，王通，侯召旭，胡金山. 冻融灰岩能量演化规律及分段损伤模型. 科学技术与工程. 2024(29): 12658-12666 . 百度学术
11.	郭威，温韬，贾文君，全志，王熠辉. 冻融作用下寒区砂岩力学特性劣化规律及数值分析. 矿业研究与开发. 2024(11): 144-154 . 百度学术
12.	田森，赵映，司鹄，朱淳，李全贵. 寒区露天矿岩质边坡裂隙岩体冻融损伤特征及力学特性试验研究. 煤炭学报. 2024(12): 4687-4700 . 百度学术
13.	高红梅，李洪伟，杨帆，徐立. 基于Maxwell分布的冻融砂岩本构模型研究. 黑龙江科技大学学报. 2023(02): 287-293 . 百度学术
14.	赵志波. 冻融条件下隧道围岩单轴蠕变力学特性试验及本构模型. 黑龙江科技大学学报. 2023(02): 299-305 . 百度学术
15.	王体富，周宗红，宋庆友. 基于Logistic分布的岩石损伤统计模型. 有色金属(矿山部分). 2023(04): 107-113+124 . 百度学术
16.	倪苏黔，徐颖，葛进进，王凤瑶，谢昊天，丁进甫. 干–酸侵蚀下深地白砂岩动静态损伤特性研究. 岩石力学与工程学报. 2023(10): 2528-2539 . 百度学术
17.	王中文，徐颖，谢守冬，焦杨浩楠，于美鲁，谢昊天. 岩石冻融损伤细观特征数值模拟研究. 中国安全生产科学技术. 2023(11): 143-149 . 百度学术