Damage analysis method for mining rock mass based on microseismic-derived fractures and its engineering application
-
摘要: 采动条件下岩体发生渐进损伤诱使裂隙萌生、发展和贯通，继而形成导水通道诱发突水灾害。该过程涉及裂隙演化及岩石损伤等问题，使得突水灾害具有动态复杂性的特点。显然，从理论上准确解译突水通道及其演化规律是十分困难的，需要依靠现场监测和数值模拟手段。为此，从“岩体变形破裂过程中，微震现象的主要本质是裂隙的扩展”学术观点出发，建立了基于微震反演裂隙的各向异性损伤模型，并将该模型与FLAC3D数值模拟分析相结合，期望将岩体宏观力学行为与裂隙发展相联系。最后，将研究成果应用到张马屯铁矿注浆帷幕突水通道分析中：对帷幕失稳区损伤系数及损伤张量进行了分析；标定了突水通道；并从渗流–应力–损伤角度建立三维数值计算模型，研究了帷幕与采场之间围岩应力及屈服特性，确定了岩体采动诱发突水通道特征及其形成机理，以期为矿山安全开采和水治理设计提供帮助。Abstract: The progressive damage of rock masses under mining conditions will induce the initiation, development and connection of fractures, form water inrush channels, and finally induce water inrush disasters. This disastrous process involves fracture evolution and rock damage, making the water inrush disasters dynamic and complex. It is challenging to accurately interpret the evolution law of the water inrush channels in theory, which needs to rely on the field monitoring and numerical simulation. Therefore, from the theoretical point of view that "the main essence of microseismic (MS) phenomena is the propagation of fractures", an anisotropic damage model is established based on the MS data. This model is combined with FLAC3D numerical simulation analysis, which is expected to link macroscopic mechanical behavior of rock masses with fracture development. Finally, the research results are applied to the analysis of the water inrush channels of the grouting curtain in Zhangmatun Iron Mine. The damage process and the damage tensor of the instability zone are analyzed, the distribution of water inrush channels is determined, and the numerical model is established from the perspective of seepage-stress-damage. The characteristics of stress and plastic yield zone between curtain and stope are studied, and the characteristics and formation mechanism of the water inrush channels induced by mining are determined to provide help for the safe mining and water treatment design of mines.
-
Keywords:
- mine /
- microseismic monitoring /
- fracture evolution /
- seepage channel /
- anisotropic damage
-
0. 引言
矿岩采动必然造成围岩的破裂损伤引起围岩力学质的劣化，诱导裂隙萌生、发展和贯通继而形成导水通道，导致渗透性增强，诱发顶板、断层带或底板发生突水等事故[1]。从理论上准确地解译导水通道演化规律及预测突水灾害十分困难，必须依靠现场监测及数值模拟手段[2]。随着计算科学的发展，数值模拟方法在岩体突水演化及力学机理研究中得到广泛应用。在适合突水研究的数值模型中，关键是建立可描述采动岩体破裂过程的损伤演化方程，这样便可准确解译岩体损伤至形成宏观破裂的全过程，才能够深层次揭示岩体失稳突水力学本质[1]。
近些年，基于地球物理理论发展起来的高精度微震监测技术，成为监测岩体动态损伤演化的有效手段[3-4]。如果将监测数据与岩石力学分析有效地结合起来，力学模型利用实际监测数据进行验证标定，动态修正岩体参数具有重要意义[5]。
越来越多的学者开始关注基于微震数据的岩体损伤模型建立及宏观力学参数标定的研究。Young等[6]结合声发射和微震监测定量描述了隧洞开挖引起的岩体破裂密度和弹性模量变化；Xu等[7]尝试将微震数据与RFPA数值模拟相结合，根据岩石能量耗散理论，提出考虑微震损伤效应的岩体劣化准则，对锦屏一级水电站边坡稳定性进行了分析。Zhao等[8]提出了考虑微震时–空–强震源参数的损伤模型，实现了对露天转地下境界顶柱失稳过程与机理的分析。目前已开展的相关研究十分有限，还没有一个被广泛接受的模型。
据此，本文利用微震数据表征岩体失稳诱发的裂隙（由微震数据表征的裂隙在本文简称为微震派生裂隙），继而基于微震派生裂隙建立损伤模型，并将建立的损伤模型与数值模拟相结合，进行数值模拟分析。基于此，以张马屯铁矿为上述研究的工程应用案例，以其帷幕突水微震监测数据为数据依托，以微震数据为输入，动态修正岩体参数，确定研究区域的帷幕突水通道并解译其形成机理。
1. 基于微震派生裂隙的损伤模型建立
工程扰动条件下裂隙特征的详细分析是评价围岩稳定性和标定岩体力学参数的关键。Candela等[9]指出，对微震活动的连续监测有助于捕获应力重分布导致的裂隙演化。这为描述岩体的动态损伤及其各向异性搭建了桥梁。
1.1 微震派生裂隙的几何参数计算
（1）微震派生裂隙方位计算
岩体失稳破裂过程中破裂机制、能量及裂隙面几何属性等信息均可通过矩张量反演求解[10]。Gilbert[11]于1970年首次提出了矩张量的概念，定义为作用在震源点源上的等效体力的一阶矩。Backus等[12]对矩张量的概念做了进一步的发展。近年来，矩张量反演作为分析岩石破裂机制的有效工具，在地震[13]、矿山微震[14]、室内岩石破裂声发射[15]及诱导地震[16]等研究中得到了广泛应用。震源处矩张量可用矩阵的形式进行表达[17]：
$$ \mathit{\boldsymbol{u}} = \mathit{\boldsymbol{GM}}, $$ (1) 式中，矢量$\mathit{\boldsymbol{u}}$由传感器记录的位移序列中的P波初动振幅决定，是一个n维的矩阵；矩阵G由传感器坐标系统中的格林函数组成，是一个n×6的矩阵。
裂隙面法向n和运动矢量v可由矩张量M的主轴求解，表达式如下：
$$ \left. {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{n}} = \sqrt {\frac{{{M_1} - {M_2}}}{{{M_1} - {M_3}}}} {\mathit{\boldsymbol{e}}_1} + \sqrt {\frac{{{M_2} - {M_3}}}{{{M_1} - {M_3}}}} {\mathit{\boldsymbol{e}}_3}, }\\ {\mathit{\boldsymbol{v}} = \sqrt {\frac{{{M_1} - {M_2}}}{{{M_1} - {M_3}}}} {\mathit{\boldsymbol{e}}_1} - \sqrt {\frac{{{M_2} - {M_3}}}{{{M_1} - {M_3}}}} {\mathit{\boldsymbol{e}}_3}。} \end{array}} \right\} $$ (2) 式中M1，M2和M3为矩张量的3个特征值，满足M1≥M2≥M3，对应特征向量$ {\mathit{\boldsymbol{e}}_1} $，$ {\mathit{\boldsymbol{e}}_2} $及$ {\mathit{\boldsymbol{e}}_3} $分别表示T轴（张拉轴），N轴（中间轴）和P轴（压缩轴）。
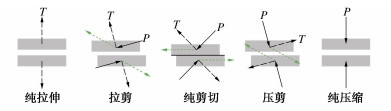
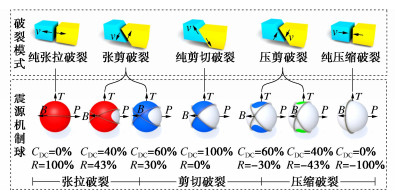
在地震学领域的术语中，单个震源的法向n和运动矢量v所确定的两个面叫做节面，也可称为震源面，其中一个是研究所需的裂隙面，另一个叫做辅助面。n与v的可互换性使得矩张量具有对称性的特点，这是由震源模型的基本假定决定的。Zhao等[18]对7个具有代表性的震源机制的震源面即n与v进行求解，给出了不同破裂机制下的震源面的分布情况，如图 1震源球中的褐色面所示。图 1中CDC表示矩张量的双力偶成分（可代表岩体的剪切破裂或断层的相对错动机制），R值为Feignier等[19]提出的基于矩张量分解的岩石破裂机制区分指标，$ R $＞$ 30% $时震源为张拉破裂，$ - 30{\text{% }} \leqslant R \leqslant 30% $时为剪切破裂，$ R $＜$ - 30% $为压缩破裂。
从图 1中可以看出，裂隙面的方向信息、运动信息与矩张量的成分密切相关。纯张拉或纯压缩破裂时，震源面是平行的，其他破裂机制下震源面成一定的角度。那么如何从法向n和运动矢量v中确定出合理的裂隙法向则是确定裂隙方位的关键。笔者[20]前期建立了不同破裂机制下的裂隙失稳倾向性指标来确定裂隙方位，总结如下：
剪切破裂机制下裂隙失稳倾向性指标
$$ {T_{\text{s}}} = \tau /{\sigma _{\text{n}}} , $$ (3) 张拉破裂机制下裂隙失稳倾向性指标
$$ {T_{\text{t}}} = ({\sigma _1} - {\sigma _{\text{n}}})/({\sigma _1} - {\sigma _3})\; , $$ (4) 压缩破裂机制下裂隙失稳倾向性指标
$$ {T_{\text{c}}} = ({\sigma _{\text{n}}} - {\sigma _3})/({\sigma _1} - {\sigma _3}) , $$ (5) 作用在裂隙面上的剪应力与正应力取决于主应力分布和裂隙方位：
$$ {\sigma _{\text{n}}} = {\sigma _1}{l^2} + {\sigma _2}{m^2} + {\sigma _3}{n^2} , $$ (6) $$ \tau ={[{({\sigma }_{1}-{\sigma }_{2})}^{2}{l}^{2}{m}^{2}+{({\sigma }_{2}-{\sigma }_{3})}^{2}{m}^{2}{n}^{2}+{({\sigma }_{1}-{\sigma }_{3})}^{2}{l}^{2}{n}^{2}]}^{1/2}。 $$ (7) 式中l，m和n为裂隙在主应力$ {\sigma _1} $，$ {\sigma _2} $和$ {\sigma _3} $轴上的法向余弦。若$ {\sigma _1} $，$ {\sigma _2} $和$ {\sigma _3} $未知，则可通过主应力反演的方法求出，具体方法可参阅文献[18]。
（2）微震派生裂隙尺度计算
可借助Brune模型求出微震派生裂隙的尺度，以裂隙半径$ {r_{\text{s}}} $表示，其与经衰减校正的地震谱的拐角频率$ {f_{\text{c}}} $有关[21]：
$$ {r_{\text{s}}} = \frac{{{K_{\text{c}}}{\beta _0}}}{{2{\text{π }}{f_{\text{c}}}}} , $$ (8) 式中，$ {K_{\text{c}}} $为依赖于震源模型的常数，$ {\beta _0} $为震源区的S波波速。对于S波$ {K_{\text{c}}} $取2.01，对于P波$ {K_{\text{c}}} $取1.32。
（3）微震派生裂隙开度计算
由岩体破裂时裂隙的运动特性描述可知，岩体发生破裂会引起裂隙的扩张与闭合，即会引起裂隙开度的变化，如图 2所示。岩石发生张拉破裂时引起裂隙的扩张，开度增大；发生压缩破裂时引起裂隙的闭合，开度减小。
![]()
图 2 几种岩石破裂机制下裂隙运动形态Figure 2. Fracture movement patterns under different rock failure mechanisms根据图 2所描述的微震派生裂隙的运动特性，联合微震派生裂隙的尺度求解公式，笔者在文献[18]中推导了微震派生裂隙开度的求解公式：
$$ \Delta \alpha = \bar u{\rm{cos}}\theta = \frac{{{M_{kk}}4\pi {\rm{ }}f_{\rm{c}}^2\cos \theta }}{{K_{\rm{c}}^{\rm{2}}\beta _0^2(3\lambda + 2\mu )\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{v}}}}, $$ (9) $$ {M_{kk}} = {M_1} + {M_2} + {M_3}, $$ (10) $$\left. {\begin{array}{*{20}{l}} {\lambda = \frac{{E\nu }}{{(1 + \nu )(1 - 2\nu )}}, }\\ {\mu = \frac{E}{{2(1 + \nu )}}。} \end{array}} \right\} $$ (11) 式中${M_{kk}}$和$ \Delta \alpha $分别为矩张量的迹和裂隙开度改变量；$\lambda $和$\mu $为拉梅系数；E，$ \nu $和$\theta $分别为弹性模量、泊松比及n和v的夹角；当岩体发生张拉破裂时，$ \Delta \alpha $为正，表示裂隙的扩张，反之，$ \Delta \alpha $为负，表示裂隙的闭合。
至此，便给出了微震派生裂隙的尺度、开度及方位计算方法。
1.2 损伤模型建立
Kawamoto等[22]提出了基于裂纹体积密度的损伤变量定义方法。本文将该方法与微震数据所反演裂隙相结合，进行各向异性损伤模型的建立。该模型即可反映岩体初始状态下的损伤，同时又能考虑岩体采动扰动所引起的损伤。
原生裂隙确定的损伤公式如下：
$$ {\mathit{\boldsymbol{D}}_{{\rm{natural}}}} = \sum\limits_{i = 1}^M {{\mathit{\boldsymbol{D}}_i}} = \frac{1}{V}\sum\limits_{i = 1}^M {\left[ {{{\bar b}_i}({\mathit{\boldsymbol{n}}_i} \otimes {\mathit{\boldsymbol{n}}_i})\sum\limits_{k = 1}^N {{S_{k, i}}} } \right]} 。 $$ (12) 式中${\mathit{\boldsymbol{D}}_{{\text{natural}}}}$为原生裂隙组的总体损伤；${\mathit{\boldsymbol{D}}_i}$为各裂隙组的损伤张量；V为研究区域的岩体体积；${\bar b_i}$为第i组裂隙的平均开度；${\mathit{\boldsymbol{n}}_i}$为第i组裂隙的平均法向；$ \otimes $为向量并矢符号；M为裂隙组数；N为裂隙数量；${S_{k, i}}$为第i组第k条裂隙的面积。
由微震派生裂隙得出的损伤张量可表示为
$$ {\mathit{\boldsymbol{D}}_{{\text{MS}}}} = \frac{1}{V}\sum\limits_{i = 1}^N {\left[ {{S_i} \cdot {b_i}({\mathit{\boldsymbol{n}}_i} \otimes {\mathit{\boldsymbol{n}}_i})} \right]} 。 $$ (13) 式中V为计算域的岩体体积；i为第i个微震派生裂隙；${S_i}$和${b_i}$分别为利用1.1节求解方法确定的微震派生裂隙的面积和开度改变量；${\mathit{\boldsymbol{n}}_i}$为微震派生裂隙的法向。
因此，对于发生破裂损伤的岩体而言，其总的损伤张量${\mathit{\boldsymbol{D}}_{{\text{total}}}}$由原生裂隙的损伤张量${\mathit{\boldsymbol{D}}_{{\text{natural}}}}$和微震派生裂隙的损伤张量${\mathit{\boldsymbol{D}}_{{\text{MS}}}}$组成：
$$ {\mathit{\boldsymbol{D}}_{{\text{total}}}} = {\mathit{\boldsymbol{D}}_{{\text{natural}}}} + {\mathit{\boldsymbol{D}}_{{\text{MS}}}}。 $$ (14) 考虑到工程计算的复杂性和本文探索性研究的目的，假设在微震派生裂隙形成前岩体只受原生裂隙的损伤影响。岩石损伤会导致材料的刚度和强度的劣化，黏聚力、内摩擦角及弹性模量与损伤程度之间的关系难以量化。因此，本文假定弹性模量、黏聚力和内摩擦角具有相同的损伤程度。
岩体损伤是一个动态过程，故岩体单元损伤不是一个单步过程，而是多步损伤的叠加。因此，当前时间步岩体单元对应损伤后的弹性模量$ E_i^{\text{D}} $、黏聚力$ c_i^{\text{D}} $和内摩擦角$ \varphi _i^{\text{D}} $可表示为
$$ E_i^{\text{D}} = E_i^0(1 - {D_{\text{i}}}^{(k)}) , $$ (15) $$ c_i^{\text{D}} = c_i^0(1 - D_i^k), $$ (16) $$ \tan \varphi _i^{\text{D}} = \tan \varphi _i^0(1 - D_i^k), $$ (17) 式中，$D_i^k$为方向i第k步累积损伤，$ E_i^0 $，$c_i^0$和$\varphi _i^0$分别为无损伤时的i方向弹性模量、黏聚力和内摩擦角。
2. 工程概况与微震数据
2.1 工程概况
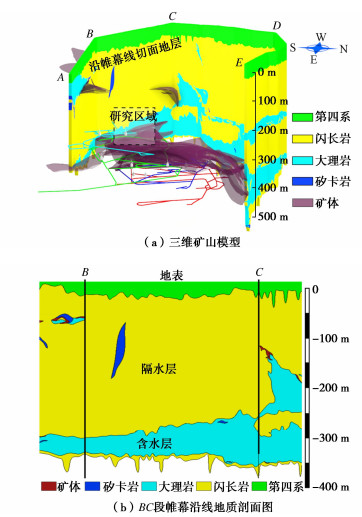
张马屯铁矿水文地质条件极其复杂，是中国少见的大水矿床。矿区地层主要为闪长岩、大理岩和第四系覆盖层（图 3）。其中大理岩岩溶裂隙发育、富水性强、透水性较好，为含水层。闪长岩含水弱、透水差，为相对隔水层。随着开采深度的增加，排水量及水害隐患不断增加。为保证安全生产，该矿于1996年进行了帷幕钻孔注浆堵水工程，整个帷幕堵水工程共施工241个钻孔，全长1410 m，深度330~560 m，厚l0 m左右，形成一个“匚”字型将矿体包围，帷幕位置及岩层分布如图 3所示。帷幕按照方位被分为南区帷幕（AB）、西南区帷幕（BC）、西区帷幕（CD）以及北区帷幕（DE）。该矿区主要含水层为-280~-500 m大理岩层，以BC段岩性最弱，富含溶洞及裂隙且距离采场最近，为重点监测区域（图 3）。
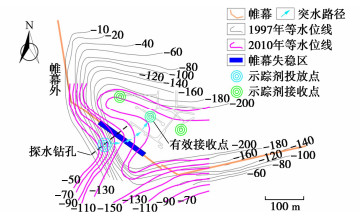
随着开采活动的不断进行，开采位置逐渐靠近西南区BC段帷幕，矿山涌水量开始明显增加，帷幕的堵水效果减弱。图 4给出了1997年及2010年的水位变化曲线，可以发现：西南区BC段帷幕中段的水力梯度发生了十分明显的变化，2010年的-180 m水位线较1997年的-180 m水位线延伸至帷幕内近60 m，表明该区域帷幕的堵水效果大大减弱，发生了帷幕突水问题。微震监测系统捕捉到了突水位置。根据水力梯度的变化可推断西南区BC段帷幕出现了连接帷幕内外的突水通道，如图 4中箭头所示。同时，在该区域进行了现场连通试验[23]，通过投放与接收高锰酸钾示踪剂（投放点与接收点位置见图 4），投放点和接收点之间连通性相对较好，径流路径比较简单且较长，证明西南区BC段帷幕存在导水构造，是帷幕的薄弱区。此外，在该区域也进行了瞬变电磁探测[23]，证明了帷幕薄弱区的存在。
![]()
图 4 1997年和2010年-324 m水位排水试验水位等值线Figure 4. Contours of water level in drainage tests on level of -324 m in 1997 and 20102.2 微震数据
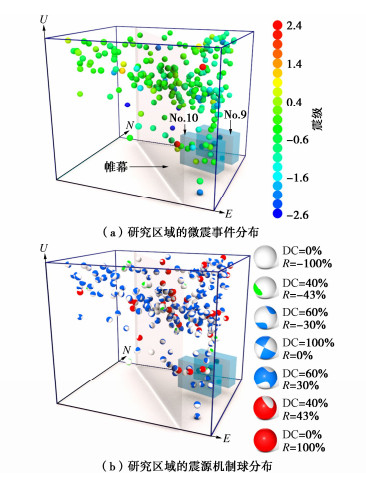
选择帷幕突水阶段的微震数据进行分析，图 5（a）给出了2007年07月24日—2009年03月17日期间记录的微震事件分布。利用文献[18]中所描述的矩张量求解方法，对研究区域进行震源机制反演，结果如图 5（b）所示（蓝色表示剪切破坏、红色表示张拉破坏、绿色表示压缩破坏）。从图 5（b）中可以发现，研究区域岩体以剪切破裂为主，该机制主要是由采矿活动和裂隙中充填物的高压水弱化引起的。张拉破裂主要是由采场顶板的高压水注入引起的裂隙张开和膨胀，以及采场顶板应力重分布导致顶板围岩局部拉应力集中造成的。No.9和No.10采场周围的微震事件主要是由采矿活动引起的。微震事件在西南区BC段帷幕呈带状分布，表明该区域帷幕出现了裂隙带。如果这些裂隙相互连通，在帷幕内外巨大水压差的作用下，易形成突水通道。研究区域微震事件的时空演化过程不是本文的研究重点，不再赘述（该部分内容可参阅文献[24]）。本文的核心是如何利用研究区域的微震数据建立损伤模型，并据此深入分析帷幕失稳区域的损伤过程及突水通道的形成机制。
3. 帷幕突水通道成因分析
3.1 结构面调查及REV确定
对研究区域围岩结构面进行调查，是确定岩体力学参数和获取式（14）中原生裂隙损伤张量的基础。本文借助奥地利Startup公司开发的ShapeMetriX3D岩体几何参数三维不接触测量系统，在研究区域工作面附近选择具有代表性的测点进行测试分析。该系统可精细化获取岩体大量、详实的几何测量数据，记录围岩表面实际岩体不连续面的几何信息，如迹长、倾向、倾角及间距等参数。研究区域结构面统计分析结果见表 1所示。
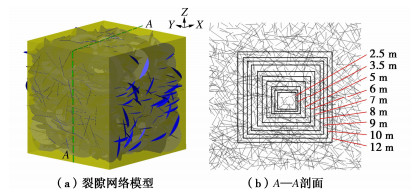
表 1 研究区域结构面几何参数Table 1. Geometric parameters of discontinuities structural plane in study areaID 倾向/(°) 倾角/(°) 迹长/m 间距/m 断距/m 分布类型 均值 标准差 分布类型 均值 标准差 分布类型 均值 标准差 分布类型 均值 标准差 分布类型 均值 标准差 1 正态 278.05 20.9 对数正态 58.52 11.3 负指数 1.11 0.48 负指数 0.61 0.70 均布 0.28 0.21 2 正态 118.23 77.9 正态 77.53 22.1 对数正态 1.41 0.41 负指数 0.27 0.24 均布 0.30 0.14 3 正态 144.30 78.2 对数正态 40.78 23.1 负指数 1.62 0.43 负指数 0.54 0.44 均布 0.34 0.17 根据表 1的统计信息，利用蒙特卡洛方法生成三维等效裂隙网络，结果见图 6（a）。然后，选择某一特定平面作为剖切面（如图 6（b）中的A—A剖面），得到垂直摄影平面的二维裂隙网络图，裂隙网络图的区域为20 m×20 m，见图 6（b）。
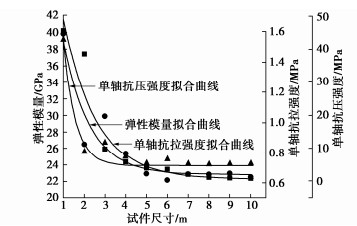
在同一个裂隙岩体样本中，以某一固定点为中心来选取不同尺寸的岩体进行尺寸效应分析。对每一种尺寸的模型，做单轴拉伸和压缩数值模拟计算，获得其弹性模量、单轴抗拉和抗压强度。岩样的力学参数随试样尺寸的变化情况如图 7所示。由图 7中力学参数变化趋势可知，REV尺寸可取8 m×8 m× 8 m。
3.2 损伤系数演化过程分析
在不考虑损伤方向性时，损伤张量${{\boldsymbol{D}}_{{\text{total}}}}$可通过三个损伤主值${D_1}$，${D_2}$和${D_3}$的几何平均值表达，称为等效损伤系数：
$$ D = \sqrt[3]{{{D_1} \cdot {D_2} \cdot {D_3}}} 。 $$ (18) 由裂隙所获得的损伤值与实际损伤值存在差别，需要对该损伤值进行标定。岩体的实际损伤系数D可以表述为
$$ D = \alpha \sqrt[3]{{{D_1} \cdot {D_2} \cdot {D_3}}} , $$ (19) 式中，$\alpha $可称为转换系数，是建立原生裂隙和微震派生裂隙与损伤系数的桥梁，可表示为岩体破坏过程中用于驱动裂隙发展的能量释放率。在有限的岩体区域内$\alpha $变化很小，可假定研究区域内的$\alpha $为常数。$\alpha $可通过反算的方法进行求解，具体求解方法可参阅文献[8]，经计算本文研究区域取30.2。
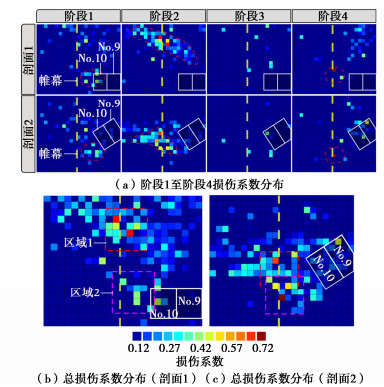
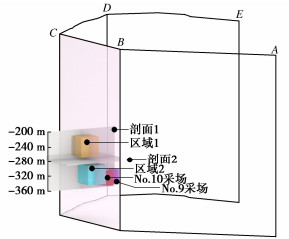
利用式（14），（18）及（19）对研究区域进行损伤系数求解，式（14）中的计算域岩体体积V取3.1节求得的REV体积。为了便于分析帷幕突水通道形成过程，将监测时间区间分为4个阶段：阶段1（2007年07月24日—2007年12月01日）、阶段2（2007年12月02日—2008年02月01日）、阶段3（2008年02月02日—2008年06月20日）、阶段4（2008年06月21日—2009年03月27日）。No.9采场在阶段1和阶段2开采，No.10采场在阶段4开采。帷幕附近围岩损伤过程见图 8，图 8（a）中的剖面分布以及图 8（b）中的两个损伤集中区域（区域1和2）的空间位置见图 9。
![]()
图 8 研究区域损伤系数的时空变化Figure 8. Temporal-spatial variation of damage coefficient in study area![]()
图 9 研究区域剖面、帷幕、损伤密集区域及采场的空间关系Figure 9. Spatial relationship among profile, curtain, damage intensive zone and stope in study area阶段1：随着No.9采场（距离帷幕水平距离103m）开采，岩体损伤主要集中于No.9和No.10采场上方及No.10采场南部，采场周围损伤系数处于中等水平。同时，在爆破损伤下，采场上部-200~-240 m帷幕周围出现零星分布的局部损伤，损伤程度较低。
阶段2：随着No.9采场的不断开采，在采动爆破损伤与高水压联合作用下，岩体强度不断劣化，裂隙受到水的润滑作用，抗剪能力降低。-220~-275 m损伤聚集程度及强度增大，该区域帷幕正好位于透水层（图 3（b））顶部区域。由此可见，本阶段已形成由帷幕西南方延伸到帷幕东北方的损伤带。该损伤带与图 4中测定的突水通道基本一致[23]。经现场测试，该阶段测试的巷道涌水量增加了3×104 m3/月[24]。
阶段3：本阶段No.9采场开采完毕，帷幕附近没有采矿活动进行，新萌生的裂隙较少，围岩损伤程度较弱，出现了一个不活跃的阶段。
阶段4：本阶段No.10采场（距离帷幕71 m）开始回采，No.10采场西侧围岩、帷幕-318 m附近出现高震级微震事件（图 5（a）），损伤程度较高（图 8），增大了帷幕与采场之间的裂隙贯通程度，形成了另一条突水通道，该阶段巷道涌水量增加4×104 m3/月[24]。
3.3 帷幕失稳区损伤张量分析
微震派生裂隙的形成不仅会改变损伤系数（主值）的大小，还会改变损伤主轴方向。为研究微震派生裂隙对帷幕附近围岩损伤方向的影响，利用式（14）对图 9中区域1与2两个损伤密集区进行损伤张量分析。
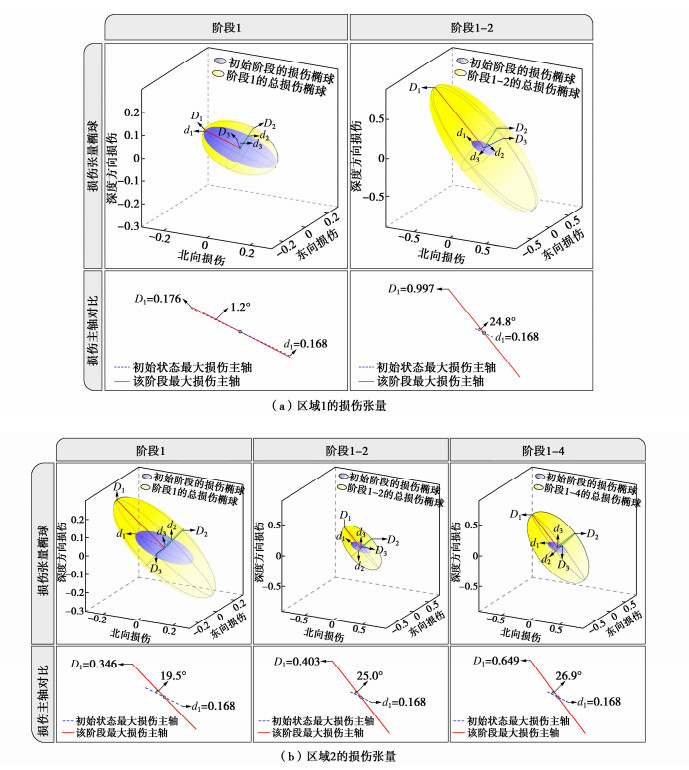
研究区域损伤张量的分布如图 10所示，图中蓝色椭球表示初始阶段损伤张量即原生裂隙所求出的损伤张量，黄色椭球为对应阶段的总损伤张量（包含了原始裂隙及微震派生裂隙的损伤张量）。图中3个轴的长度表示损伤主值的大小，轴的方向表示损伤主值的方向。从图 9中可以看出，区域1在阶段3和4无新增损伤，区域2在阶段3无新增损伤。因此，图 10（a）只给出了区域1在阶段1和阶段1-2的损伤张量，图 10（b）只给出了区域2在阶段1、阶段1-2以及阶段1-4的损伤张量：
![]()
图 10 帷幕失稳区域1与区域2的损伤张量Figure 10. Damage tensors of Zones 1 and 2 in curtain instability zone（1）在阶段1中，岩体损伤程度较低，所引起的裂隙体积改变较小，损伤主方向主要由原生裂隙决定。帷幕失稳区域1中最大的损伤主轴较原生裂隙的损伤最大主轴仅发生了1.2°的偏转，最大损伤主值由0.168仅增大到了0.176。由于帷幕失稳区域2靠近No.9采场，受采动影响最大的损伤主轴发生19.5°的偏转，最大损伤主值由0.168增大到0.346。
（2）进入阶段2后，受采动爆破损伤及高压水的影响，微震派生裂隙对损伤张量的影响程度增大，帷幕失稳区域1的最大损伤主轴偏转角增大到24.8°，损伤主值增大到0.997。帷幕失稳区域2受No.9采场采动影响，损伤主值进一步增大，最大损伤主轴偏转角也进一步增大。帷幕失稳区域1和2，微震事件密集分布，形成具有优势分布方位的微震派生裂隙，造成损伤主轴偏转，增强了帷幕失稳区导水性，形成突水通道。
（3）进入阶段3后，帷幕附近没有采矿活动进行，帷幕失稳区1和2的损伤张量无明显变化。
（4）进入阶段4后，No.10采场开始采矿，帷幕失稳区域2出现高损伤区域，损伤主值增大到0.649，最大损伤主轴偏转角增大到26.9°，但较阶段2变化较小。表明阶段2中具有优势方位的微震派生裂隙进一步聚拢，导水性增强。
由此可见，岩体损伤带来了裂隙开度与方位的变化，改变了原生裂隙的贯通程度和各向异性程度，增强了裂隙的导水性，帷幕失稳区域1与2形成突水通道。该区域分布与图 4通过排水试验、现场连通试验及瞬变电磁探测确定[23]的突水通道一致。
3.4 帷幕失稳破坏数值模拟分析
本节利用微震监测与数值模拟相结合的方法，将1.2节建立的损伤模型嵌入数值模拟中，进行三维数值计算，圈定帷幕失稳区域，从力学角度解译张马屯铁矿帷幕失稳突水通道的形成机理。
（1）数值模型建立及边界条件
根据张马屯铁矿矿区工程地质资料，包括矿区工程地质剖面图、帷幕区工程地质剖面图及帷幕区各钻孔等资料建立三维数值模型。最终建立的三维数值模型如图 11所示，包含了2438280个单元。本构模型设置为Mohr-Coulomb模型，采用的岩体力学参数见表 2。
表 2 张马屯铁矿岩体力学参数Table 2. Mechanical parameters of rock masses of Zhangmatun Iron Mine岩体名称 块体密度/(g·cm-3) 渗透系数/(10-7m·s-1) 抗拉强度/MPa 内摩擦角φ/(°) 弹性模量/GPa 泊松比$ \nu $ 第四系 1.97 1920 — 35 0.037 0.25 闪长岩 2.76 5.78 8.9 36 53.8 0.21 大理岩 2.72 2315 6.1 36 45.2 0.29 矿体 3.35 4.20 6.9 38 30.5 0.15 帷幕 2.40 2.32 2.8 35 25.0 0.24 边界条件设定包括位移和渗流边界。位移边界设定：计算模型底部和侧面分别采用总位移约束和固定位移约束，计算模型顶部为自由边界。渗流边界设定：面ABCD，AacD，abcd为水压力面，水压力分布为
$$ p = \rho g(33 - z) , $$ (20) 式中，33为地表高程（m），z为深度（m），p为水压（Pa），$ \rho $为密度（kg/m3），g为重力加速度（m/s2）。
ABab面为大气表面，相对压力为零；DCdc面因为距采空区较远，岩性为闪长岩，为相对隔水层，故将该面假定为不透水面；BbdC面为对称面，经现场测试水头高度为-20 m。在开挖边界上，施加0.1 MPa的水压来模拟大气压力。
利用FISH语言将3.2节中求得的岩体损伤系数D，按照微震事件发生的时空顺序映射到岩体计算单元中，根据式（15）~（17）动态修正数值模拟单元的弹性模量、黏聚力和内摩擦角，同时结合采矿活动进行数值计算。微震数据与岩体单元的映射过程如图 12所示。
（2）应力与塑性区分布
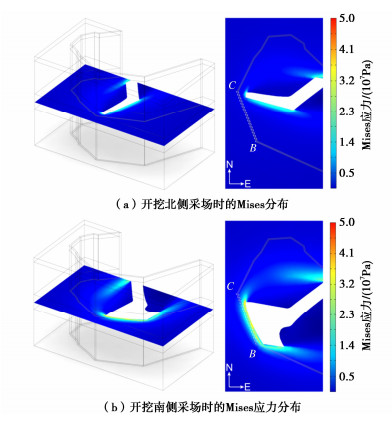
通过数值模型获得的Mises应力分布，见图 13。图 13（a）为开采No.9和No.10采场北侧矿体时的Mises应力分布，图 13（b）为开采No.9和No.10采场及其周边采场时的Mises应力分布。从图中可以得出，应力主要集中于采场开挖边界，采场越靠近帷幕，帷幕周边的应力集中程度越大。从图 13（b）中可以得出，西南区BC段帷幕应力集中明显，帷幕内外应力差达数10 MPa。从图 3地层关系可知，应力集中区域为透水区且岩体较破碎，在高应力差下易形成突水通道，发生突水事故。
![]()
图 13 -330 m水平Mises应力分布Figure 13. Mises stress distribution at a depth of -330 m level图 14给出了-330 m水平岩体塑性区分布状态。图 14中不同的颜色表示不同的岩体单元状态，红色表示张拉破坏，青色表示剪切破坏，蓝色表示弹性状态。围岩破坏区主要位于开挖边界沿线。张拉破坏区位于采场北部和南部边界，而剪切破坏区位于西南区BC段帷幕边界，表明西南区BC段帷幕失稳区是由剪切破坏引起的。该失稳区与现场测试[23]得出的帷幕失稳区域一致。同时，从图 14中不难发现，帷幕破坏是帷幕和采场开挖边界之间距离较短造成的，即突水通道的形成过程受到采矿活动与帷幕之间距离的显著影响。因此，在帷幕和开挖边界之间保持足够的距离对保持帷幕的挡水效果至关重要。对于西南区BC段帷幕失稳区域，可通过帷幕附近硐室向失稳区打注浆钻孔进行补幕注浆来恢复阻水效果。
![]()
图 14 -330 m水平岩体单元状态Figure 14. Plastic state of rock mass unit at a depth of -330 m level4. 结论
（1）基于微震派生裂隙体积密度，建立了考虑原生裂隙和微震派生裂隙的各向异性损伤模型，给出了数值模拟与微震监测相结合的分析方法。
（2）以张马屯铁矿帷幕突水为研究案例，对研究区域的损伤过程进行了研究。研究表明西南区BC段帷幕受采场采动及高水压影响出现了两处失稳区域，形成了突水通道。通过损伤张量分析得出，具有优势方位的微震派生裂隙改变了原生裂隙的贯通程度和各向异性程度，增强了裂隙的导水性，形成了帷幕突水区域。
（3）通过帷幕失稳破坏数值模拟分析得出，突水通道的形成过程主要受采矿活动与帷幕间距的影响。帷幕与采场之间的剪切破坏带形成了突水通道。因此，帷幕与采场之间预留足够的距离是维持帷幕堵水效应的关键。
（4）通过微震数据表征裂隙，继而建立损伤模型，使得现场监测与数值分析有机的结合起来，可成为识别潜在突水通道和解译突水通道形成机理的一种合适方法。
-
![]()
图 2 几种岩石破裂机制下裂隙运动形态
Figure 2. Fracture movement patterns under different rock failure mechanisms
![]()
图 4 1997年和2010年-324 m水位排水试验水位等值线
Figure 4. Contours of water level in drainage tests on level of -324 m in 1997 and 2010
![]()
图 8 研究区域损伤系数的时空变化
Figure 8. Temporal-spatial variation of damage coefficient in study area
![]()
图 9 研究区域剖面、帷幕、损伤密集区域及采场的空间关系
Figure 9. Spatial relationship among profile, curtain, damage intensive zone and stope in study area
![]()
图 10 帷幕失稳区域1与区域2的损伤张量
Figure 10. Damage tensors of Zones 1 and 2 in curtain instability zone
![]()
图 13 -330 m水平Mises应力分布
Figure 13. Mises stress distribution at a depth of -330 m level
![]()
图 14 -330 m水平岩体单元状态
Figure 14. Plastic state of rock mass unit at a depth of -330 m level
表 1 研究区域结构面几何参数
Table 1 Geometric parameters of discontinuities structural plane in study area
ID 倾向/(°) 倾角/(°) 迹长/m 间距/m 断距/m 分布类型 均值 标准差 分布类型 均值 标准差 分布类型 均值 标准差 分布类型 均值 标准差 分布类型 均值 标准差 1 正态 278.05 20.9 对数正态 58.52 11.3 负指数 1.11 0.48 负指数 0.61 0.70 均布 0.28 0.21 2 正态 118.23 77.9 正态 77.53 22.1 对数正态 1.41 0.41 负指数 0.27 0.24 均布 0.30 0.14 3 正态 144.30 78.2 对数正态 40.78 23.1 负指数 1.62 0.43 负指数 0.54 0.44 均布 0.34 0.17 
下载: 导出CSV
表 2 张马屯铁矿岩体力学参数
Table 2 Mechanical parameters of rock masses of Zhangmatun Iron Mine
岩体名称 块体密度/(g·cm-3) 渗透系数/(10-7m·s-1) 抗拉强度/MPa 内摩擦角φ/(°) 弹性模量/GPa 泊松比ν 第四系 1.97 1920 — 35 0.037 0.25 闪长岩 2.76 5.78 8.9 36 53.8 0.21 大理岩 2.72 2315 6.1 36 45.2 0.29 矿体 3.35 4.20 6.9 38 30.5 0.15 帷幕 2.40 2.32 2.8 35 25.0 0.24
下载: 导出CSV
-
[1] 杨天鸿, 唐春安, 谭志宏, 等. 岩体破坏突水模型研究现状及突水预测预报研究发展趋势[J]. 岩石力学与工程学报, 2007, 26(2): 268–277. doi: 10.3321/j.issn:1000-6915.2007.02.007 YANG Tian-hong, TANG Chun-an, TAN Zhi-hong, et al. State of the art of inrush models in rock mass failure and developing trend for prediction and forecast of groundwater inrush[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 268–277. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.02.007
[2] 刘超, 吴顺川, 程爱平, 等. 采动条件下底板潜在导水通道形成的微震监测与数值模拟[J]. 北京科技大学学报, 2014, 36(9): 1129–1135. https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201409001.htm LIU Chao, WU Shun-chuan, CHENG Ai-ping, et al. Microseismic monitoring and numerical simulation of the formation of water inrush pathway caused by coal mining[J]. Journal of University of Science and Technology Beijing, 2014, 36(9): 1129–1135. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJKD201409001.htm
[3] 姜福兴. 微震监测技术在矿井岩层破裂监测中的应用[J]. 岩土工程学报, 2002, 24(2): 147–149. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200202003.htm JIANG Fu-xing. Application of microseismic monitoring technology of strata fracturing in underground coal mine[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 147–149. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200202003.htm
[4] 庄端阳, 唐春安, 梁正召, 等. 基于微震能量演化的大岗山右岸边坡抗剪洞加固效果研究[J]. 岩土工程学报, 2017, 39(5): 868–878. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705014.htm ZHUANG Duan-yang, TANG Chun-an, LIANG Zheng-zhao, et al. Reinforcement effect of anti-shear tunnels of Dagangshan right bank slope based on microseismic energy evolution[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 868–878. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705014.htm
[5] 钱波, 杨莹, 徐奴文, 等. 白鹤滩水电站左岸边坡岩石损伤变形反馈分析[J]. 岩土工程学报, 2019, 41(8): 1464–1471. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201908013.htm QIAN Bo, YANG Ying, XU Nu-wen, et al. Feedback analysis of rock damage deformation of slope at left bank of Baihetan Hydropower Station[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(8): 1464–1471. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201908013.htm
[6] YOUNG R P, COLLINS D S, REYES-MONTES J M, et al. Quantification and interpretation of seismicity[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1317–1327. doi: 10.1016/j.ijrmms.2004.09.004
[7] XU N W, DAI F, LIANG Z Z, et al. The dynamic evaluation of rock slope stability considering the effects of microseismic damage[J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 621–642. doi: 10.1007/s00603-013-0432-5
[8] ZHAO Y, YANG T H, YU Q L, et al. Dynamic reduction of rock mass mechanical parameters based on numerical simulation and microseismic data-A case study[J]. Tunnelling and Underground Space Technology, 2019, 83: 437–451. doi: 10.1016/j.tust.2018.09.018
[9] CANDELA T, WASSING B, TER HEEGE J, et al. How earthquakes are induced[J]. Science, 2018, 360(6389): 598–600. doi: 10.1126/science.aat2776
[10] 明华军, 冯夏庭, 张传庆, 等. 基于微震信息的硬岩新生破裂面方位特征矩张量分析[J]. 岩土力学, 2013, 34(6): 1716–1722. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201306030.htm MING Hua-jun, FENG Xia-ting, ZHANG Chuan-qing, et al. Moment tensor analysis of attitude characterization of hard rock newborn fracture surface based on microseismic informations[J]. Rock and Soil Mechanics, 2013, 34(6): 1716–1722. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201306030.htm
[11] GILBERT F. Excitation of the normal modes of the earth by earthquake sources[J]. Geophysical Journal of the Royal Astronomical Society, 1971, 22(2): 223–226. doi: 10.1111/j.1365-246X.1971.tb03593.x
[12] BACKUS G, MULCAHY M. Moment tensors and other phenomenological descriptions of seismic sources Ⅱ. Discontinuous displacements[J]. Geophysical Journal of the Royal Astronomical Society, 1976, 47(2): 301–329. doi: 10.1111/j.1365-246X.1976.tb01275.x
[13] STIERLE E, VAVRYČUK V, ŠÍLENÝ J, et al. Resolution of non-double-couple components in the seismic moment tensor using regional networks Ⅰ: a synthetic case study[J]. Geophysical Journal International, 2014, 196(3): 1869–1877. doi: 10.1093/gji/ggt502
[14] 李庶林, 林恺帆, 周梦婧, 等. 基于矩张量分析的特大山体破坏前兆孕震机制研究[J]. 岩石力学与工程学报, 2019, 38(10): 2000–2009. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910007.htm LI Shu-lin, LIN Kai-fan, ZHOU Meng-jing, et al. Study on failure precursors and seismogenic mechanisms of a large landslide based on moment tensor analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(10): 2000–2009. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910007.htm
[15] 王笑然, 李楠, 王恩元, 等. 岩石裂纹扩展微观机制声发射定量反演[J]. 地球物理学报, 2020, 63(7): 2627–2643. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX202007013.htm WANG Xiao-ran, LI Nan, WANG En-yuan, et al. Microcracking mechanisms of sandstone from acoustic emission source inversion[J]. Chinese Journal of Geophysics, 2020, 63(7): 2627–2643. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX202007013.htm
[16] MARTÍNEZ-GARZÓN P, KWIATEK G, BOHNHOFF M, et al. Impact of fluid injection on fracture reactivation at The Geysers geothermal field[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(10): 7432–7449. doi: 10.1002/2016JB013137
[17] AKI K, RICHARDS PG. Quantitative seismology, theory and methods[M]. New York: W. H. Freeman, 1980.
[18] ZHAO Y, YANG T H, ZHANG P H, et al. Inversion of seepage channels based on mining-induced microseismic data[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 126: 104180. doi: 10.1016/j.ijrmms.2019.104180
[19] YOUNG R P, MAXWELL S C, URBANCIC T I, et al. Mining-induced microseismicity: monitoring and applications of imaging and source mechanism techniques[J]. Pure and Applied Geophysics PAGEOPH, 1992, 139(3/4): 697–719.
[20] ZHAO Y, YANG T H, ZHANG P H, et al. Method for generating a discrete fracture network from microseismic data and its application in analyzing the permeability of rock masses: a case study[J]. Rock Mechanics and Rock Engineering, 2019, 52(9): 3133–3155.
[21] MENDECKI A J. Seismic monitoring systems[M]//Seismic Monitoring in Mines. Dordrecht: Springer Netherlands, 1997: 21–40.
[22] KAWAMOTO T, ICHIKAWA Y, KYOYA T. Deformation and fracturing behaviour of discontinuous rock mass and damage mechanics theory[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1988, 12(1): 1-30.
[23] 韩伟伟, 李术才, 张庆松, 等. 矿山帷幕薄弱区综合分析方法研究[J]. 岩石力学与工程学报, 2013, 32(3): 512–519. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201303010.htm HAN Wei-wei, LI Shu-cai, ZHANG Qing-song, et al. A comprehensive analysis method for searching weak zones of grouting curtain in mines[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(3): 512–519. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201303010.htm
[24] ZHOU J R, YANG T H, ZHANG P H, et al. Formation process and mechanism of seepage channels around grout curtain from microseismic monitoring: a case study of Zhangmatun iron mine, China[J]. Engineering Geology, 2017, 226: 301–315.
-
期刊类型引用(9)
1. 曹安业，王常彬，杨旭，王冰，张宁，赵卫卫. 微震定位精度影响下采场裂隙表征与冲击地压预警. 煤炭科学技术. 2024(02): 1-9 . 
百度学术
2. 许延春，黄磊. 基于微震监测的工作面底板突水全时空预警方法. 煤炭科学技术. 2023(01): 369-382 . 百度学术
3. 李新旺，温学君，代卫林，程立朝，孙利辉. 大埋深倾斜厚煤层下导水裂隙带发育高度的微震监测. 中国科技论文. 2023(05): 526-533 . 百度学术
4. 王杰，袁国涛. 不同加载速率下深部砂岩的声发射与破裂响应特征. 采矿与岩层控制工程学报. 2023(04): 65-76 . 百度学术
5. 袁国涛，张明伟，王杰，卫俊，杨坤. 采动覆岩微震分区演化特征的数值模拟研究. 煤炭科学技术. 2023(08): 36-46 . 百度学术
6. 赵扬锋，丁玲，刘玉春，李兵. 循环荷载作用下煤岩电荷感应与微震信号变化规律. 水资源与水工程学报. 2023(05): 172-182 . 百度学术
7. 余伊河，马立强，张东升，苏发强，王文. 长壁工作面采动覆岩层理开裂机理及侧向裂隙发育规律. 煤炭学报. 2023(S2): 527-541 . 百度学术
8. 邹建. 地质指标分析下的裂隙岩体渗透系数估算模型构建. 科学技术创新. 2022(23): 35-38 . 百度学术
9. 董陇军，邓思佳，闫艺豪. 岩体失稳灾害人机环系统监测与灾害防控——智能安全人机工程学及教学实践. 安全. 2021(10): 1-10+89 . 百度学术
其他类型引用(10)
计量
- 文章访问数: 215
- HTML全文浏览量: 42
- PDF下载量: 106
- 被引次数: 19
