0.   引言

土体的动模量作为衡量土体产生变形难易程度的指标,也是场地地震反应分析的必备参数,在土体动力分析时扮演着重要的角色^[1]。通常借助共振柱、动三轴、剪切仪或扭剪仪等室内试验设备对土体进行动力加载,可得到土体的动应力-动应变曲线（滞回圈）,采用土体滞回圈两端顶点连线斜率表示动模量^[2-3]。但即便在仪器传感器足够灵敏的情况下,每种室内试验都只能得到部分应变范围的动模量,例如：共振柱试验能得到土体10^-6～10^-4应变范围的动剪切模量；动三轴或扭剪试验能得到土体10^-4～10^-2应变范围的动弹性（剪切）模量^[3-4]。因此,为了完整地描述土体动模量随应变的变化情况,经常会借助共振柱和动三轴对土体进行联合测试。但由于动弹性模量和动剪切模量之间需要泊松比建立关系,且众多学者经研究表明,土体泊松比随着应变幅值的变化而变化^[5-6],这使得两种试验所得的结果无法直接串联。梁珂等^[7]基于相关函数理论提出了动模量阻尼比的新算法,该方法有效拓宽了动模量在动三轴试验中的应变测试范围。但在实际应用中,由于涉及到部分较为复杂的计算公式,需要事先编写程序才能简便使用。

另外,作为一种典型的非线性材料,在应变幅值较大的情况下,部分土体存在着拉、压模量不一致的情况,该特性在滞回圈上表现为滞回圈的不对称性^[8]。但常规的滞回圈算法是基于理想的等效线性动黏弹性模型推导得出的,无法准确计算不对称滞回圈的模量。Kumar等^[9]针对大应变滞回圈不对称的情况,将滞回圈视为拉、压两个部分,然后单独计算拉、压模量。然而Kumar仅使用该方法计算加载第一周的动模量,对于分级加载是否适用未做进一步的探究。因此在已有传感器精度的条件下,需要寻找一个简单有效,同时能计算大应变下土体拉、压模量的计算方法。

本文以黏土为试验对象,基于最小二乘法原理对小应变下的滞回圈进行拟合,有效地减少小应变下白噪声对模量计算的影响,提高结果的可信度。同时在Kumar模量计算方法的基础上进行修正,使其能准确计算大应变下、非线性特征较强的非对称滞回圈的拉、压模量。

1.   动模量计算方法

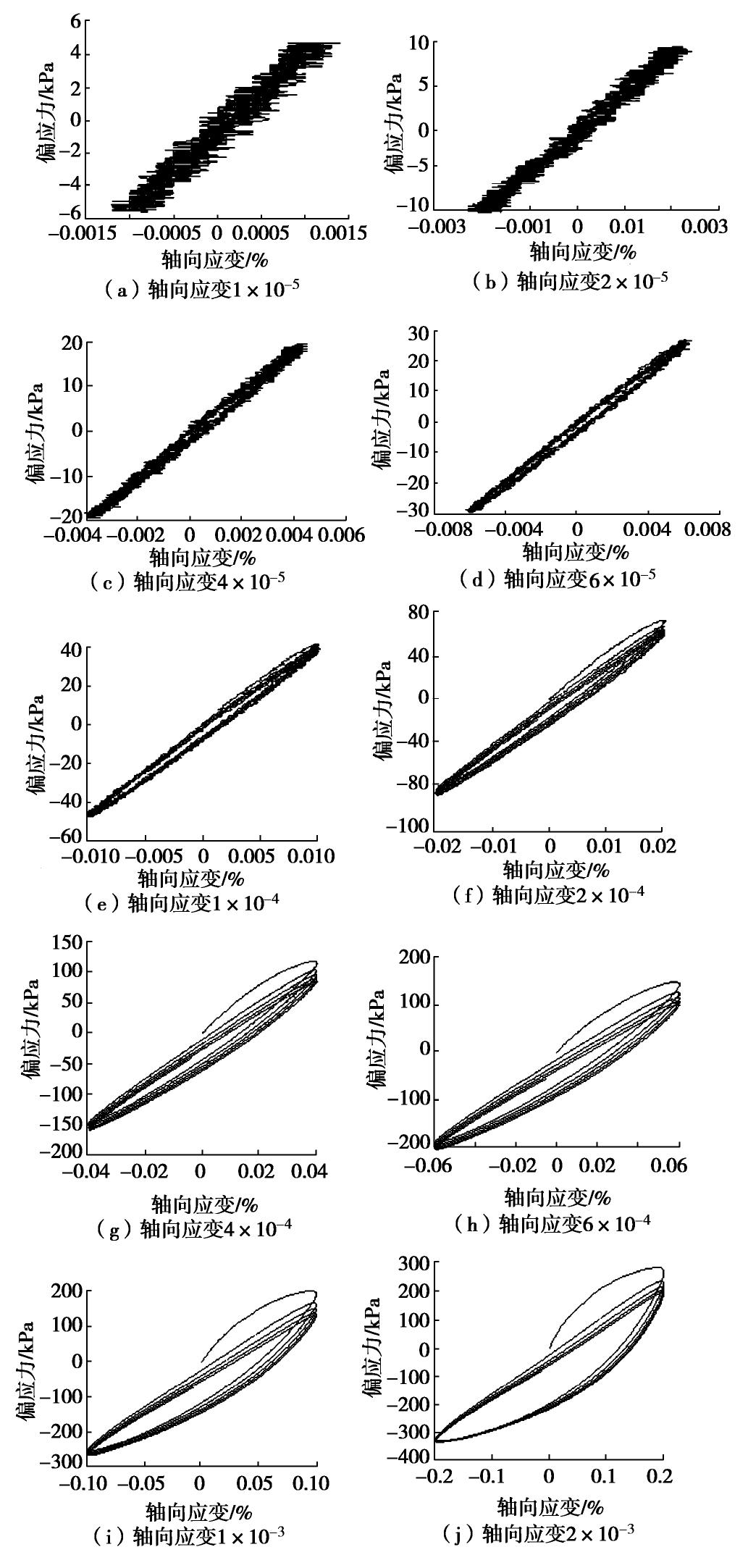
为了探究非对称滞回圈拉、压模量的计算方法,于南京地区采集黏土样本开展动三轴试验,取样深度为53.2～53.4 m。根据经验公式：${\sigma }_{\text{c}}=\text{20}$$H\text{/3}$ (kPa),将试样的有效围压设为400 kPa,固结24 h。式中,${\sigma }_{\text{c}}$为等效固结围压（kPa）；H为埋置深度（m）,其基本物理参数如表1所示。

表  1  黏土物理参数

Table  1.  Physical parameters of clay

颗粒相对密度	液限/%	塑限/%	塑性指数	天然含水率/%	天然密度/(g·cm-3)
2.72	34	21	13	12	1.95

下载: 导出CSV 

| 显示表格

将试样于削样台制成直径5 cm、高10 cm的实心试样,拟对试样施加1×10^-5～2×10^-3应变范围的动荷载,开展动三轴应变控制分级加载试验,每级施加5圈等幅应变荷载,加载频率为0.5 Hz。李晓飞^[10]认为,试样中的累积孔压对模量存在影响,为了避免前期小应变加载产生的累积孔压对后续的模量测试产生影响,于试样四周贴上滤纸条,便于试样排出多余的孔隙水,维持试样内部孔压的稳定。最终试验所得各级应变的滞回圈如图1所示。

图  1  各级应变的滞回圈

Figure  1.  Hysteresis loops of strain at all levels

下载: 全尺寸图片 幻灯片

从图1可以看出,当应变小于4×10^-5时,滞回圈受随机振动干扰明显、表面粗糙；当应变大于6×10^-5时,滞回圈受到干扰的程度逐渐减弱,表面逐渐光滑。此外,当应变幅值较小时,土体近似呈线弹性状态,随着应变的增大,尤其是当应变大于4×10^-4时,土体非线性特征愈发显著,且滞回圈逐渐显示非对称性。

1.1   小应变下最小二乘法拟合计算模量

在常规的等效线性动黏弹性模型中,土体动模量是由滞回圈两个顶点连线的斜率所表示的。但在小应变幅值的情况下由于受到环境中的随机振动、电信号干扰等因素,导致试验采集数据不稳定。

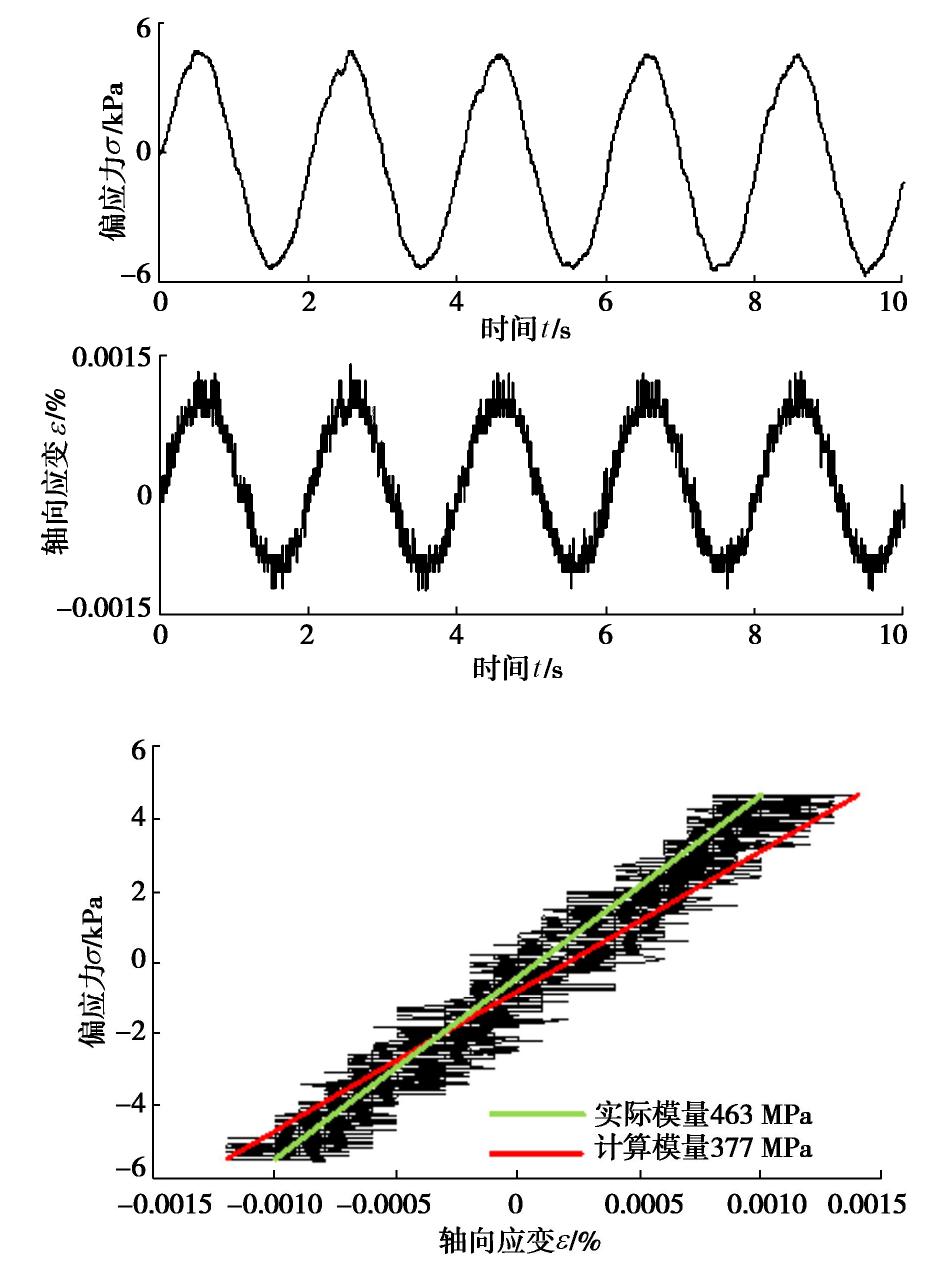
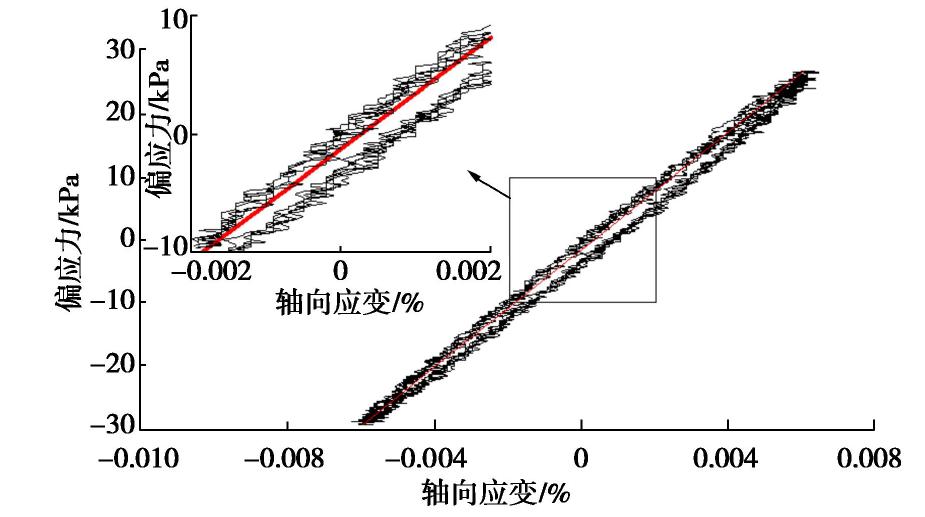
以1×10^-5应变量级下的试验曲线为例,由于应变幅值小,其应变时程曲线受白噪声干扰显著（如图2所示）,最终导致滞回圈受到较为严重的干扰。假设仍以传统的滞回圈法计算,则得到的计算结果为377 MPa（如图2红线所示）,然而这显然与实际模量（如图2绿线所示）存在较大差距。为了减少白噪声对小应变下模量计算的干扰,提高准确率,借助最小二乘法拟合计算动模量。

图  2  1×10^-5应变量级下试验曲线

Figure  2.  Test curves at 1×10^-5 strain level

下载: 全尺寸图片 幻灯片

设小应变下土体在i时刻的动应力-动应变关系满足

若将前n个时刻的式（1）累加可得

而若在式（1）的两端同时乘以该时刻对应的应变可得

同样的,将前n个时刻的式（3）累加可得

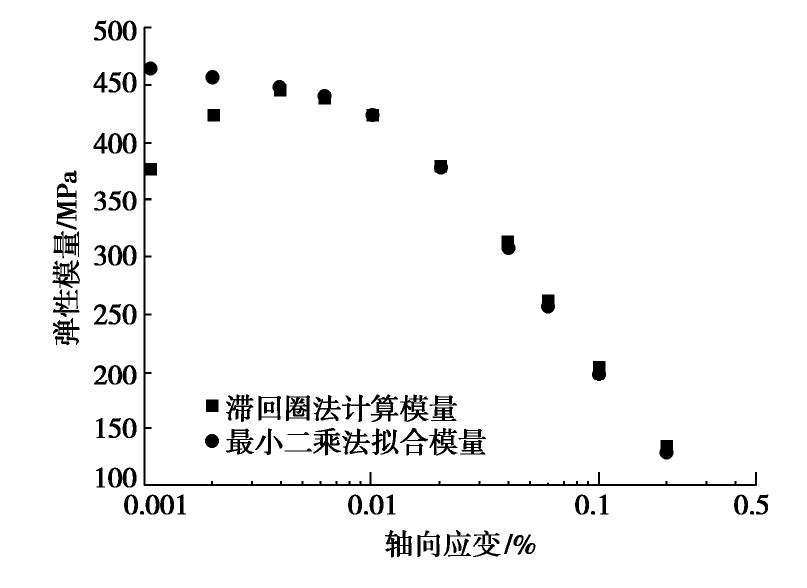
式中 n为试验过程中每周采集点数；${\sigma }_0$为初始轴向应力；${\sigma }_i$为加载过程中i时刻的应力；${\epsilon }_i$表示应力为${\sigma }_i$时刻的应变。将式（2）、（4）联立消除含${\sigma }_0$项即可解得拟合模量$E$,最终化简公式为

计算结果如图3所示。

图  3  最小二乘法与滞回圈法计算结果对比

Figure  3.  Comparison between results of least square method and hysteretic loop method

下载: 全尺寸图片 幻灯片

图3对比了最小二乘法与滞回圈法的计算结果。由图3可知,在小应变情况下,受到白噪声的干扰,滞回圈法计算所得的模量偏小。而最小二乘法对滞回圈斜率进行线性拟合能够较好的描述小应变下土体模量的变化情况。而随着应变逐渐增大,白噪声对应变测量精度的干扰逐渐减少,因此两种算法的计算结果逐渐接近。当应变等于1×10^-4时,拟合模量与滞回圈法计算模量几乎一致,此时滞回圈清晰可见,几乎不受白噪声影响。此方法原理简单、易于直接使用,且一定程度上减小了噪声对于动模量的影响,使得小应变情况下所得模量更符合实际。

1.2   大应变下修正Kumar法计算模量

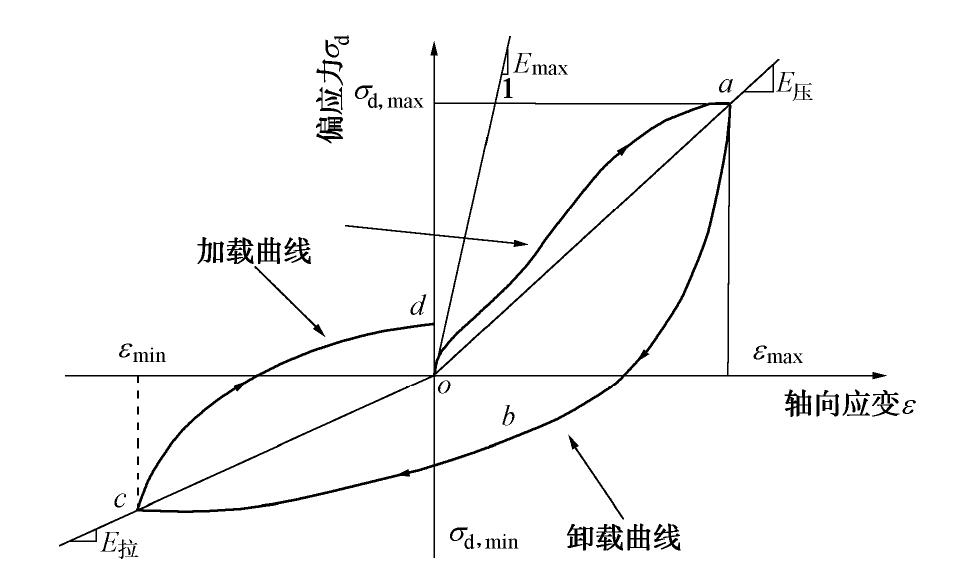
当应变幅值逐渐增大时,土体逐渐进入非线性阶段,此时滞回圈的非对称性不断增强。为了计算具有明显非线性特征时土体滞回圈的拉、压模量,Kumar^[9]给出了一种新的模量计算方式,计算原理示意图如图4所示。

图  4  Kumar法计算原理

Figure  4.  Calculation principle of Kumar method

下载: 全尺寸图片 幻灯片

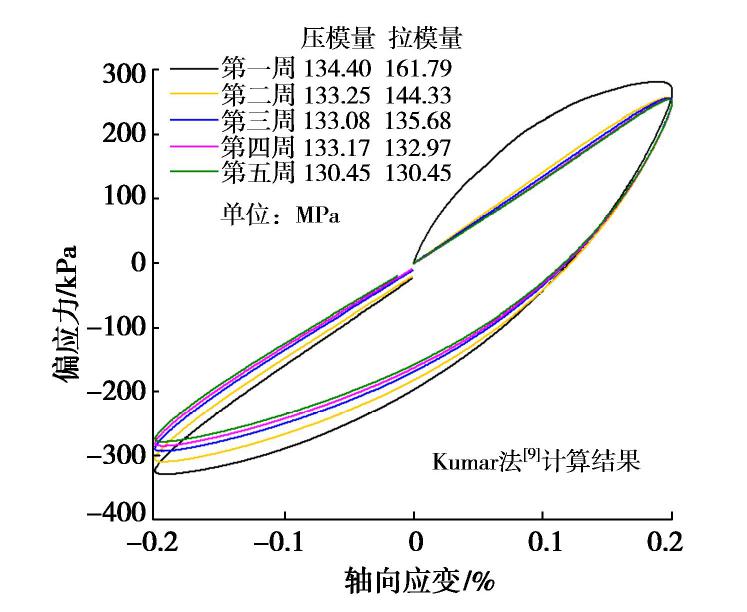
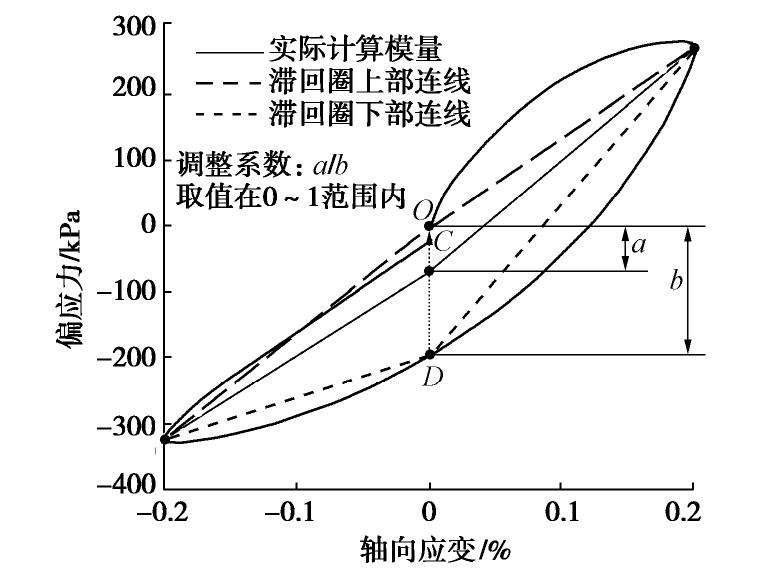
Kumar法将滞回圈起点与压方向的顶点连线的斜率作为动压缩模量$E_{压}$（图4中线段oa的斜率）,与拉方向顶点连线的斜率作为动拉伸模量$E_{拉}$（图4中线段oc的斜率）。以2×10^-3应变幅值时的滞回圈作为测试,每周滞回圈以及Kumar法计算结果如图5所示。

图  5  2×10^-3应变量级下Kumar法计算结果

Figure  5.  Calculated results of Kumar method at 2×10^-3 strain level

下载: 全尺寸图片 幻灯片

由图5可知,若按照Kumar法直接计算大应变下滞回圈拉、压模量,会出现拉模量大于压模量的结果。然而已有研究表明,黏土的非线性显著,且抗压强度高于抗拉强度^[11],这使得计算结果与实际情况相违背。这是因为Kumar法默认滞回圈的起点是从骨架曲线原点出发,而在实际加载过程中,由于前期小应变的应力加载,导致试样产生了一定的累积塑性应变。虽然在每一应变量级加载前都会重新固结,恢复固结状态,但滞回圈仍然难以从新的骨架曲线原点出发。为了解决这一问题,尝试对Kumar法进行修正,修正方法如图6所示。

图  6  修正Kumar法计算原理

Figure  6.  Calculation principle of modified Kumar method

下载: 全尺寸图片 幻灯片

将滞回圈起点作为O点,向下作垂线与滞回圈卸载曲线相交于D点,C为线段OD中的某一点。当C点在骨架曲线原点处时,便能根据C点与两端顶点连线准确计算出拉、压模量。若C点偏高,则会导致拉模量偏大、压模量偏小；若C点偏低,则会导致拉模量偏小、压模量偏大。为了找到C点位置,定义调整系数为a/b,即OC/OD,从而描述C点的位置,取值范围在0～1。在理想的等效线性动黏弹性模型中,调整系数为0.5,然而在不对称性较强的滞回圈中,调整系数的值仍需进一步讨论。

由各级应变下的滞回圈可知,当应变不大于1×10^-4时,土体非线性特征较弱,此时土体经历的荷载扰动较小,并且几乎没有塑性应变产生,更接近于土体的初始状态。此外,小应变下的土体更近似于线弹性材料,其滞回圈两端连线应经过骨架曲线原点。因此,可以借助小应变时土体的滞回圈求得骨架曲线原点的位置,即C点的位置。

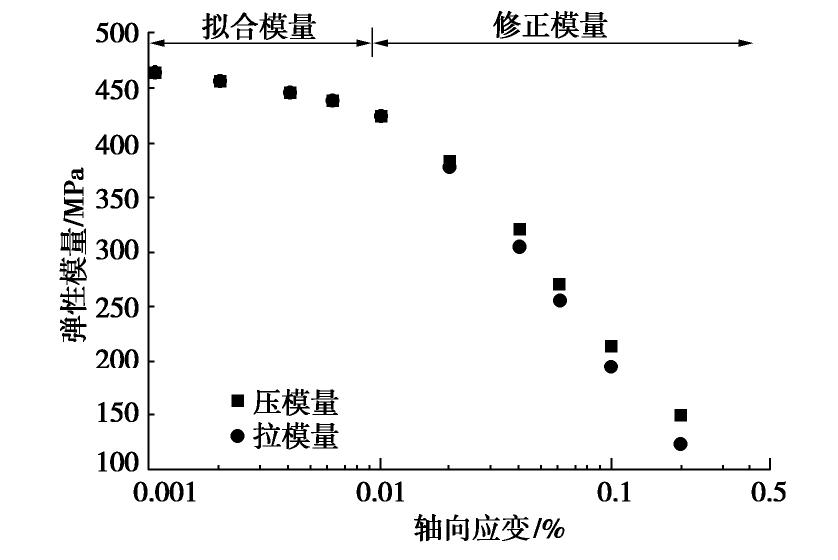
图7展示了6×10^-5应变量级下的滞回圈。将滞回圈两端顶点连线得到如图红线,然后如图6所述方式计算调整系数,最终所得调整系数为0.21。鉴于调整系数是在小应变情况下计算得出,因此既能对大应变情况下拉、压模量起到修正作用,又能保证小应变时拉模量等于压模量,从而与最小二乘法拟合所得模量相吻合。将所得调整系数应用于大应变下拉、压模量的计算,再将小应变下最小二乘法拟合所得的模量相结合,得到的计算结果如图8所示。

图  7  6×10^-5应变量级下滞回圈

Figure  7.  Hysteresis loops at 6×10^-5 strain stage

下载: 全尺寸图片 幻灯片

图  8  两种方法共同计算动模量的结果

Figure  8.  Results of dynamic modulus calculated by two methods

下载: 全尺寸图片 幻灯片

从图8可知,采用小应变下计算调整系数,然后应用于大应变时拉、压模量计算的方法能有效修正Kumar法,使得计算结果更为真实可信。而两种方法的组合也能较好地描述不对称滞回圈的拉、压模量的变化情况。

最终将计算方法总结为：在小应变情况下,修正的Kumar模型会由于白噪声的干扰导致计算所得模量偏小,因此采用最小二乘法对此时的模量进行拟合。此时土体近似于线弹性,可认为拉模量等于压模量；当应变逐渐增大时,土体非线性特征逐渐显现,最小二乘法与滞回圈法均无法准确描述模量变化情况。因此先借助小应变时的滞回圈计算调整系数,再采用修正Kumar方法计算大应变时的拉、压模量。将两种计算方法所得模量进行组合,共同完成较宽应变范围的模量计算。

2.   结论

无论是小应变幅值下受白噪声干扰显著的滞回圈,还是大应变下非对称特征显著的滞回圈,常规的滞回圈法在计算动模量时均容易出现失真。针对此问题,本文提出使用最小二乘法和修正Kumar法联合计算宽应变范围、非对称滞回圈动模量的计算方法,得到以下3点结论。

（1）使用最小二乘法拟合能够有效克服小应变时白噪声对模量计算的影响,使得动三轴的模量测试范围能向前延伸至1×10^-5。

（2）在小应变情况下计算调整系数,然后计算动模量的修正Kumar法能有效计算大应变时非对称滞回圈的拉、压模量。

（3）采用小应变使用最小二乘法拟合、大应变使用修正Kumar法的联合计算方式能够兼具两者优势：延伸计算应变宽度的同时,解决非对称滞回圈模量计算不准确的问题。