0.   引言

锚杆已广泛应用于深基坑^[1]、高边坡^[2]、地下建筑抗浮^[3]等工程，但仍以传统拉力型锚杆应用为主。随着国家工程建设的发展与技术需求，一些新型锚杆技术^[3-5]相继研发成功，并推广应用于实际工程，取得了良好的经济效益和锚固效果。

国内外学者对传统锚杆进行了大量研究，取得了较多的研究成果。尤春安^[6]利用Mindlin问题的位移解求解了全长黏结式锚杆受力的弹性解，并分析了锚杆受力特征及影响因素与规律。黄明华等^[7]推导了锚杆锚固段的双指数曲线剪切滑移模型及其拉拔荷载传递解答，进而分析了其荷载传递规律与荷载位移曲线特征。何思明等^[8]求解了预应力锚杆在其界面完全黏结、脱黏阶段的剪应力分布，阐述了预应力锚杆的荷载传递特性。叶观宝等^[9]研究了在外部荷载作用下，锚杆锚固段各单元体中的荷载分布特征与有效受压锚固段长度，发现常规张拉方法下锚杆各单元受力不均。刘永权等^[10]开展了多种类型锚杆的现场破坏性试验，发现了界面峰值剪应力进入塑性状态后，峰值剪应力逐渐向锚固体中部转移的现象。

汪文武等^[11]利用FLAC^3D对锚杆的拉拔过程进行了模拟分析，研究发现锚杆的锚固效应与锚固剂的摩擦角、黏结力及有效围压存在线性正比例关系，锚固剂所受的剪切应力分布规律随锚杆拉拔过程而改变。任非凡等^[12]采用ABAQUS对多界面复合锚杆拉拔试验进行数值模拟研究，发现随着锚杆受力的增加，锚杆前端的握裹力被克服，剪切应力峰值向后移动。Ma等^[13]采用非连续变形法（DDA）和有限元法（FEM），对锚杆与岩土体界面的黏结滑移过程进行了数值分析，得到了轴向力分布、剪力分布和拉拔位移曲线的变化规律。郭金刚等^[14]基于残余剪切强度的全长黏结锚杆拉拔模拟，研究了锚杆与锚固剂接触面残余剪切强度、剪切刚度系数和黏结长度对锚杆支护效果的影响。赵同彬等^[15]采用PFC颗粒流软件对锚杆界面力学试验开展仿真模拟，发现界面剪应力沿轴向先增大后减小。

但是，上述研究成果大多都针对传统的全黏结型锚杆。随着《建筑工程抗浮技术标准》^[16]在2020年正式实施，规定对抗浮锚杆灌浆体的裂缝控制进行设计，也对锚固浆体的轴向拉应力提出了要求，引起了广大工程师及科研人员的关注。与传统全黏结型锚杆相比，拉压复合型锚杆^[5]的锚固段由承压锚固段与受拉锚固段共同组成，二者协同承载，其承载性能明显提升，更能在抗浮工程领域发挥积极作用。但是，对拉压复合型锚杆承压锚固段荷载传递机理、界面剪应力传递机理、灌浆体轴向应力分布规律等仍有待进一步研究，以推动其在抗浮工程中的应用。

因此，本文以拉压复合型锚杆现场试验^[5]为基础，对其开展数值模拟分析，拟进一步揭示拉压复合型锚杆在荷载传递规律、灌浆体轴向应力分布以及协同承载机理，为拉压复合型锚杆的设计提供参考。

1.   数值模型及验证

1.1   数值模型建立

本文以文献[5]中的现场试验为基础，采用有限差分软件FLAC^3D，分别对全黏结型锚杆（T型）、压力型锚杆（C型）、拉压复合型锚杆（TC型）建立数值计算模型。筋体和承载体弹性模量均取200 GPa，泊松比0.20，重度78.5 kN/m³。灌浆体弹性模量取20 GPa，泊松比0.25，重度23.0 kN/m³。模型尺寸高度6.0 m，宽度6.0 m，深度6.5 m，孔口预留自由段0.5 m，锚固段为3.0 m。

土体采用莫尔-库仑模型，灌浆体采用线弹性本构模型。土体与灌浆体均采用实体单元，筋体采用Cable单元，承载体采用shell单元，cable单元和shell单元之间采用link进行刚性连接。灌浆体和土体之间的接触面设置Interface单元，接触面单元的法向刚度k_n、切向刚度k_s采用文献[17]的经验公式进行计算。选取了20余组参数进行计算分析，通过综合计算结果与试验结果进行对比分析，确定最终计算模型参数。其中，TC12型、TC11型、TC21型的受拉锚固段法向、切向刚度分别为130，120，110 MPa；承压锚固段法向、切向刚度分别为156，144，132 MPa。

1.2   模型验证

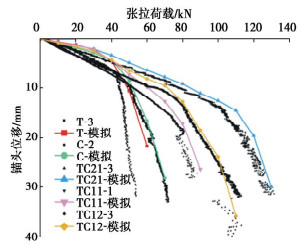
模拟计算的荷载-位移曲线与实测代表性荷载-位移曲线进行对比，如图 1所示。

图  1  荷载-位移曲线对比图

Figure  1.  Comparison of load-displacement curves

下载: 全尺寸图片 幻灯片

从图 1中可以看出，数值模拟的荷载-位移曲线分布形态整体与实测结果基本一致。T型、C型、TC21型、TC11型、TC12型锚杆的极限抗拔承载力模拟值（实测代表值）分别为40 kN（44 kN）、50 kN（52.7 kN）、110 kN（104.8 kN）、80 kN（80.8 kN）、100 kN（112.8 kN），相对误差分别为-9.1%，-5.1%，+5.0%，-1.0%，-11.3%，模拟值与试验测试值整体吻合度较好，验证数值模型及模型参数取值较为合理。

2.   内力分析

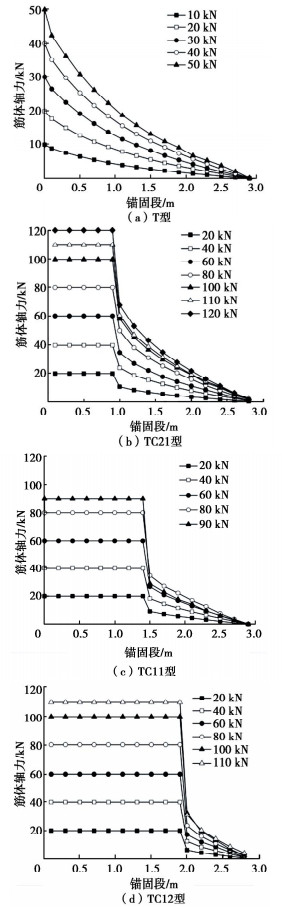
2.1   筋体轴力

图 2为计算得到的全黏结型与拉压复合型锚杆的筋体轴力分布图。从整体上看，在全黏结型锚杆的全长锚固段以及拉压复合型锚杆的受拉锚固段上，筋体轴力均沿深度方向递减，且轴力越大，递减速度越快。

图  2  锚杆筋体轴力分布

Figure  2.  Distribution of axial force in anchor bar

下载: 全尺寸图片 幻灯片

拉压复合型锚杆近锚头侧为承压锚固段，筋体与灌浆体隔离，故该长度上的筋体轴力保持不变，筋体所受轴力大小等于张拉力。由于承压锚固段分担了部分荷载，在受拉锚固段起始端的筋体所受拉力远小于端头的张拉力，轴力分布曲线表现为筋体轴力在承载体处的受拉锚固段起点出现陡降。以总拉力80 kN为例，TC21型、TC11型、TC12型拉压复合型锚杆的受拉承载系数分别为0.58，0.44，0.27，略低于相应的受拉长度系数0.67，0.50，0.33。分析其原因，可能是由于承压锚固段因受压出现灌浆体径向侧胀，引起灌浆体与土体界面法向应力增加，导致界面侧摩阻力增大，分担荷载有所增加，使受拉锚固段分担荷载相应有所减小，故而受拉承载系数略小于受拉长度系数。

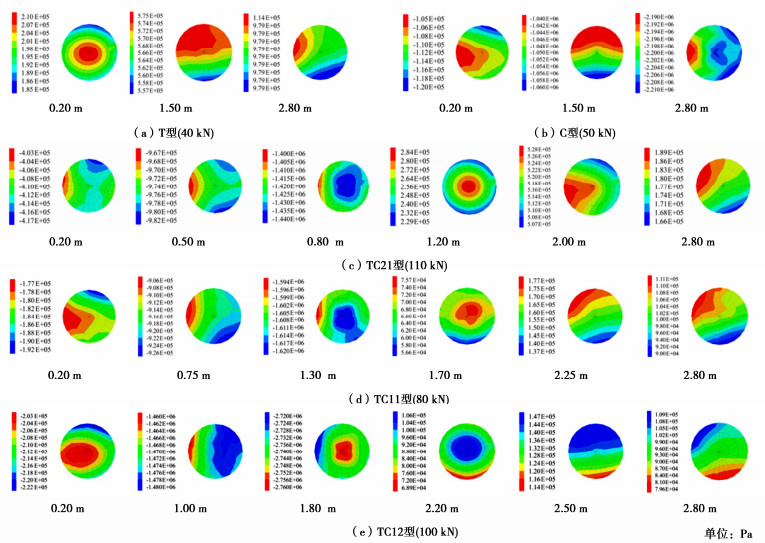
2.2   浆体轴向应力沿径向分布

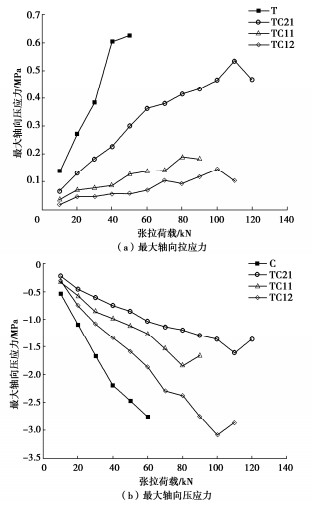
锚固段灌浆体产生轴向拉应力时，因在永久性锚固工程尤其是抗浮工程中可能因开裂诱发筋体锈蚀而备受关注。为研究不同锚杆浆体的轴向应力，分别绘制了各类型锚杆在拉力达到极限抗拔承载力时，距离锚固段端头不同位置处的灌浆体截面轴向应力分布图，如图 3所示。为便于表述，以总锚固段前端的端头记为零点，以锚固段某截面至端头的距离标记其所在位置。灌浆体截面轴向应力为正值，表示受拉应力；为负值，表示受压应力，下文均省略正负号。

图  3  锚杆灌浆体轴向应力沿径向分布图

Figure  3.  Radial distribution of axial stress in grout of anchor rebar

下载: 全尺寸图片 幻灯片

统计图 3中轴向应力最大值、最小值及相对极差（最大值和最小值的差值（极差）与最大值和最小值的平均值之比），统计结果如表 1所示，可以看出，灌浆体轴向应力为MPa级时的相对极差介于0.91%~2.82%，轴向应力分布非常均匀。尽管部分位置处的相对极差较高，但是灌浆体的轴向应力已经处于10^-1 MPa级甚至10^-2 MPa级，即轴向应力非常小，截面应力的代表值对分析影响很小，可近似认为轴向应力分布“十分均匀”。需要说明的是，由于灌浆体顶部和底部的土体应力与位移存在一定差异，浆体轴向应力沿着径向并不是均匀分布，但是，在截面上的整体分布相对均匀。综合分析，在截面上选取半径50 mm处的轴向应力可以较好地代表灌浆体截面的轴向应力。

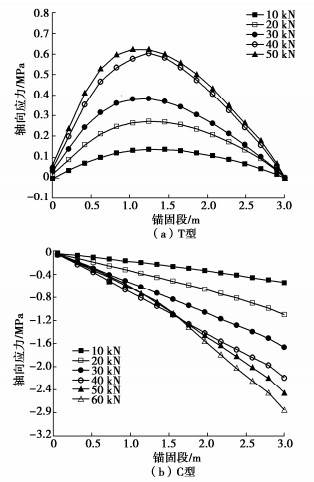
表  1  灌浆体轴向应力统计表

Table  1.  Statistics of axial stress in grouting body

锚杆类型	荷载/kN	位置/m	轴向应力/MPa		相对极差/%
			最大值	最小值
T型	40	0.20	0.210	0.185	12.66
		1.50	0.575	0.557	3.18
C型	50	0.20	0.120	0.105	13.33
		1.50	1.060	1.040	1.90
		2.80	2.210	2.190	0.91
TC21型	110	0.20	0.417	0.403	3.41
		0.50	0.982	0.967	1.54
		0.80	1.440	1.400	2.82
		1.20	0.284	0.229	21.44
		2.00	0.528	0.507	4.06
		2.80	0.189	0.166	12.96
TC11型	80	0.20	0.192	0.177	8.13
		0.75	0.926	0.906	2.18
		1.30	1.620	1.594	1.62
		1.70	0.076	0.057	28.57
		2.25	0.177	0.137	25.48
		2.80	0.111	0.090	20.90
TC12型	100	0.20	0.222	0.203	8.94
		1.00	1.480	1.460	1.36
		1.80	2.760	2.720	1.46
		2.20	0.106	0.069	42.29
		2.50	0.147	0.114	25.29
		2.80	0.109	0.080	30.69

下载: 导出CSV 

| 显示表格

2.3   浆体轴向应力沿轴向分布

绘制截面半径50 mm处的浆体轴向应力沿锚杆轴向的分布图，如图 4（T型和C型）、图 5（TC型）所示。从图 4可以看出，拉力型锚杆锚固段全长范围内的浆体均处于明显的受拉状态，且浆体轴向拉应力沿轴向分布先增大后减小，表明全黏结型锚杆灌浆体截面受到的轴向最大拉应力并不是在锚固段始端，而是向锚固段延伸一定距离。在破坏前，灌浆体轴向拉应力整体随锚杆拉力增大而明显增加。锚杆拉力由10 kN增加到20，30，40 kN时，最大轴向拉应力由0.14 MPa分别增加到0.27 MPa（+92.8%）、0.38 MPa（+171.4%）、0.60 MPa（+328.6%），增幅显著。当拉力达到50 kN时，锚杆破坏，拔出变形大幅增加，而浆体轴向应力增加十分有限，其中最大轴向拉应力仅为0.63 MPa，相比锚杆拉力40 kN时增幅仅5.0%。分析原因可能是锚杆在拔出破坏前，T型锚杆在筋浆界面与浆土界面反向剪切的双作用下，浆体剪切应变较大，导致灌浆体的轴向拉应力随锚杆拉力增加而增加。当拨出破坏时，由于浆土界面出现滑脱，土对浆的约束被削弱，浆体剪切应变的增幅削弱，导致灌浆体轴向拉应力不再随锚杆拉力增加而显著增加。

图  4  全黏结型与压力型锚杆灌浆体轴向应力的轴向分布

Figure  4.  Axial distribution of grout axial stress in tension-type and compression-type anchor

下载: 全尺寸图片 幻灯片

图  5  拉压复合型锚杆灌浆体轴向应力的轴向分布

Figure  5.  Axial distribution of grout axial stress in TC anchor

下载: 全尺寸图片 幻灯片

压力型锚杆由于筋体全长无黏结，依靠最底部承载体将筋体受到的拉力作用到灌浆体，承载体挤压灌浆体，再依靠浆土界面间黏结力传递荷载。因此，灌浆体处于受压状态，图 4（b）表明轴向应力在底部最大，在轴向近似向锚头方向线性衰减。锚杆拉力由10 kN增加到20，30，40 kN时，最大轴向压应力由0.54 MPa分别增加到1.10 MPa（+103.7%）、1.66 MPa（+207.4%）、2.18 MPa（+303.7%），随拉力增加近似线性增加。拉力增加到50 kN时，锚杆破坏，灌浆体轴向应力增幅明显减小，主要增大的长度范围也明显缩小，约至底部承载体直径6倍范围。

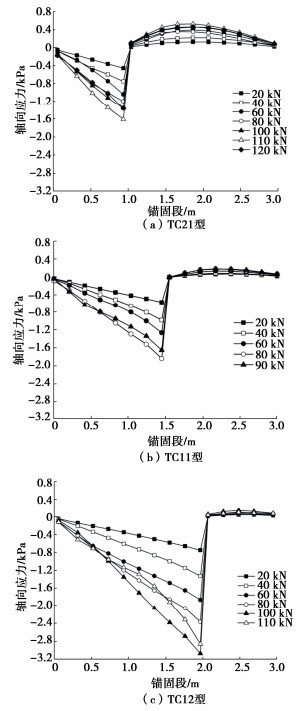
图 5为3种不同拉压长度比的拉压复合型锚杆灌浆体轴向应力沿锚杆轴向的分布图。可以明显看出，锚杆在拉拔至破坏前，灌浆体轴向应力分布曲线在承载体两侧反向分布，且轴向应力整体随荷载增加而增大。在承压锚固段长度范围内，灌浆体处于受压状态，且在承载体处最大，随至承载体距离的增加而减小，轴向压应力分布曲线近似呈线性分布。在受拉锚固段长度范围内，灌浆体处于受拉状态，轴向拉应力先增大后减小，且轴向拉应力值远小于承压锚固段上的轴向压应力值。

TC21型锚杆所受拉力由110 kN（极限抗拔承载力）增加到120 kN（破坏）时，承压锚固段灌浆体所受轴向应力明显减小，且距离承载体越近，减小幅度越大。在承载体处，最大轴向压应力由1.60 MPa减小为1.34 MPa，降幅约16.3%；受拉锚固段灌浆体所受轴向拉应力整体也有所降低，最大值由0.53 MPa减小为0.47 MPa，降幅约11.3%。

TC11型锚杆所受拉力由80 kN（极限抗拔承载力）增加到90 kN（破坏）时，承压锚固段近承载体范围的灌浆体轴向压应力明显减小，在承载体处，最大轴向压应力由1.83 MPa减小为1.65 MPa，降幅约9.8%。受拉锚固段的轴向应力变化相对较小，最大值由0.19 MPa减小为0.18 MPa，降幅仅约5.3%。

TC12型锚杆所受拉力由100 kN（极限抗拔承载力）增加到110 kN（破坏）时，承压锚固段近承载体范围的灌浆体轴向压应力减小较为显著，在承载体处，最大轴向压应力由3.07 MPa减小为2.86 MPa，降幅约6.8%。受拉锚固段的轴向拉应力最大值由0.14 MPa减小为0.10 MPa，但是由于拉应力值很小，较小的降低就会导致降幅较高，达到28.6%。

2.4   浆体最大轴向应力

进一步提取T型、C型及TC型锚杆灌浆体的最大轴向应力（包括拉应力和压应力），并分析其随张拉荷载的变化规律，如图 6所示。

图  6  灌浆体的最大轴向应力分布

Figure  6.  Distribution of maximum axial stress in grout

下载: 全尺寸图片 幻灯片

从图 6（a）可以看出，锚杆破坏前，全黏结型锚杆锚固段、拉压复合型锚杆受拉锚固段的灌浆体最大轴向拉应力都随锚杆拉力的增加而增大；且全黏结型锚杆灌浆体轴向拉应力的增幅明显高于拉压复合型锚杆。拉压复合型锚杆的拉压长度比越小，受拉锚固段的最大轴向拉应力越低。拉力小于40 kN时，拉压复合型锚杆受拉锚固段灌浆体的最大轴向拉应力显著低于全黏结型锚杆。拉力为40 kN时，T型锚杆灌浆体的最大轴向拉应力为0.63 MPa；而TC21型、TC11型、TC12型锚杆受拉锚固段灌浆体的最大轴向拉应力分别仅为0.23，0.09，0.06 MPa，仅为T型锚杆的36.5%，14.3%，9.5%，均大幅降低。其主要原因是拉压长度比决定了受拉锚固段与承压锚固段协同承载的拉力大小，相同总拉力时，受拉锚固段分担的荷载小于甚至明显小于全黏结型锚杆，故相应的最大轴向拉应力也小。而拉压长度比越小，受拉锚固段越短，分担的荷载也越小，故相应的最大轴向拉应力随拉压长度比的减小而减小。

拉压复合型锚杆在拉力为80 kN时，TC21型锚杆的受拉锚固段灌浆体最大轴向拉应力为0.41 MPa，而TC11型、TC12型分别为0.19，0.10 MPa，仅为TC21型的46.3%，24.4%。TC21型、TC11型、TC12型在各自的极限抗拔承载力下，受拉锚固段灌浆体最大轴向拉应力分别为0.53，0.19，0.15 MPa，仍小于甚至远小于全黏结型锚杆在40 kN时的最大轴向拉应力0.63 MPa。

图 6（b）表明，锚杆破坏前，压力型锚杆锚固段、拉压复合型锚杆承压锚固段的灌浆体最大轴向压应力都随锚杆所受拉力增加而增大。拉力小于60 kN时，拉压复合型锚杆承压锚固段灌浆体的最大轴向压应力明显小于压力型锚杆。拉力为50 kN时，C型锚杆灌浆体的最大轴向压应力为2.46 MPa；而TC21型、TC11型、TC12型锚杆承压锚固段灌浆体的最大轴向压应力分别为0.85，1.11，1.58 MPa，为C型锚杆的36%，45.1%，64.2%，均大幅降低，且拉压长度比越小，承压锚固段协同承载的荷载越大，最大轴向压应力越大。

拉力为80 kN时，TC12型锚杆承压锚固段灌浆体的最大轴向压应力为2.37 MPa，而TC11型、TC21型分别为1.83，1.19 MPa，仅为TC12型的77.2%，50.2%，也明显降低。

可见，在相同拉力作用下，拉压复合型锚杆灌浆体最大轴向应力远小于传统全黏结型锚杆或压力型锚杆，尤其是最大轴向拉应力可以大幅降低。拉压长度比能较好地调控灌浆体的最大轴向应力，合理优化拉压长度比设计，可以进一步显著减小灌浆体的轴向拉应力，避免灌浆体开裂。另外，承载体挤压承压锚固段灌浆体时，会同时拉动受拉锚固段灌浆体，由于筋体与灌浆体之间的高黏结力作用，承载体处不会发生开裂。因此，拉压复合型锚杆的耐久性得到显著提升。

3.   界面剪应力分布

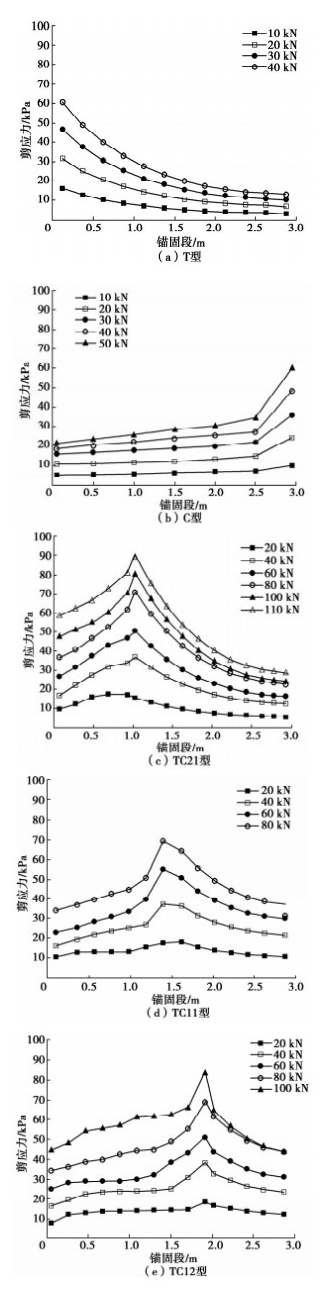
图 7为依据数值模型结果分别绘制的T型、C型及TC型锚杆的界面剪应力沿锚固段长度分布图。全黏结型锚杆浆土界面剪应力呈非线性分布，始端界面的剪应力最大，并由锚头向孔底方向递减，整体分布规律与工程实测^[10]结果基本一致。压力型锚杆浆土界面剪应力由底部承载体处向锚头方向单向传递，且随至承载体距离增大而衰减，在承载体附近衰减较为明显，而远离承载体后的浆土界面剪应力衰减较缓。在拉力达到极限抗拔承载力时，全黏结型、压力型锚杆的浆土界面剪应力峰值分别为60.45，60.29 kPa；末端最小剪应力为13.02，21.47 kPa，分别为峰值的21.5%，35.6%。

图  7  不同类型锚杆剪应力分布图

Figure  7.  Distribution of shear stress for different types of anchor

下载: 全尺寸图片 幻灯片

拉压复合型锚杆锚固段界面剪应力由承载体处同时向锚头和孔底方向传递，并随传递距离的增加而减小，且呈明显的“中间大，两头小”双向传递与分布特征。拉力为40 kN时，TC21、TC11、TC12型锚杆的浆土界面最大剪应力（在承压板附近）分别为37.39，37.58，38.62 kPa，分别仅为T型锚杆的61.9%，62.2%，63.89%，表明在相同的拉力条件下，TC型锚杆的浆土界面剪应力显著低于T型锚杆，也明显低于C型锚杆（约50 kPa），此时的应力集中现象得到明显削弱。

拉力达到极限抗拔承载力时，TC21、TC11、TC12型锚杆的浆土界面最大剪应力分别为90.49，69.72，84.35 kPa，分别为T型锚杆在拉力达到极限抗拔承载力时的1.50倍、1.15倍、1.40倍；承压锚固段始端端头的剪应力为59.05，34.49，44.90 kPa，分别为峰值的65.3%，49.5%，53.2%；受拉锚固段尾端端头的剪应力为29.01，37.54，44.17 kPa，分别为峰值的32.1%，53.8%，52.4%。由此可见，与T型及C型锚杆相比，TC型锚杆在拉力达到极限抗拔承载力时的浆土界面剪应力峰值要高，且承压锚固段始端端头的界面剪应力与峰值之比远高于C型锚杆，受拉锚固段尾端端头的界面剪应力与峰值之比远高于全黏结型锚杆。这充分表明，TC型锚杆的承压锚固段与受拉锚固段段界面摩阻力发挥水平高于荷载集中型锚杆，且沿长度方向的分布相对更加均匀，浆土界面侧摩阻力发挥更加充分。

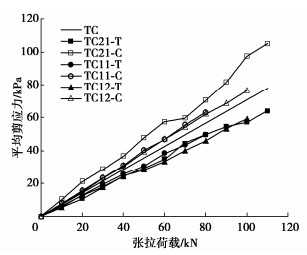
进一步分析TC型锚杆锚固段的平均剪应力如图 8所示。图 8中TC为在拉力下的总锚固段界面平均剪应力，其随张拉荷载线性增加。承压锚固段与受拉锚固段的界面平均剪应力随张拉荷载增加而增大，且3种TC型锚杆的承压锚固段界面的平均剪应力均高于受拉锚固段，高于总锚固段界面平均剪应力。TC21型锚杆的承压锚固段界面的平均剪应力最高，短锚效应最明显；而受拉锚固段的短锚效应不明显。

图  8  不同荷载下的平均剪应力

Figure  8.  Average shear stresses under different loads

下载: 全尺寸图片 幻灯片

4.   协同承载规律

4.1   受拉承载系数

拉压复合型锚杆锚头拉力通过承压锚固段范围的无黏结筋体直接传递至承载体，并在此处进行荷载转换与分配，一部分拉力通过承载体挤压承压锚固段灌浆体，再依靠承压锚固段与土体界面黏结力提供抗拔力；一部分拉力通过筋体拉动受拉锚固段灌浆体，再依靠受拉锚固段与土体界面黏结力提供抗拔力。拉压长度比分割了较长的总锚固段，形成了相对较短的承压锚固段与受拉锚固段段，并影响承压锚固段与受拉锚固段分担荷载的比例。通过计算受拉承载系数（受拉锚固段分担荷载与总张拉荷载之比），可以分析拉压复合型锚杆的协同承载规律，如图 9所示。

图  9  不同荷载作用下的受拉承载系数

Figure  9.  Tension bearing coefficient under different loads

下载: 全尺寸图片 幻灯片

TC21型锚杆受拉承载系数在拉力80 kN前的计算值与实测值吻合较好，整体不超过0.60。拉力继续增加后，实测受拉承载系数继续增加，接近极限抗拔力时大幅增加。而计算受拉承载系数的变化相对平稳，在拉力100，110，120 kN时的受拉承载力为0.54，0.55，0.53，低于受拉长度系数（受拉锚固段长度与总锚固段长度之比）0.67，但三者较为接近，计算结果表明承压锚固段与受拉锚固段趋于同步破坏。

TC11型锚杆受拉承载系数在拉力45~80 kN的计算值与实测值吻合较好，且二者整体均不超过0.50。拉力80 kN时，受拉承载系数的计算值与实测值分别为0.44，0.47，接近受拉长度系数0.50。尽管模拟计算结果在拉力超过极限抗拔承载力后，受拉承载系数下降至0.33（90 kN），但是拉力在70 kN时仍为0.44，表明受拉锚固段与承压锚固段破坏几乎同时破坏。

TC12型锚杆受拉承载系数在拉力较大时的计算值与实测值吻合较好，且在破坏前整体均不超过0.30。拉力100 kN时，受拉承载系数的计算值与实测值分别为0.28，0.39，与受拉长度系数0.33偏差不大。而模拟计算拉力为90 kN时的受拉承载系数为0.28，表明承压锚固段与受拉锚固段近似同步破坏。

整体而言，TC型锚杆在拉力达到极限抗拔承载力时，受拉承载系数的计算值与实测值吻合较好，计算结果略低于受拉长度系数，其原因可能是承压锚固段灌浆体因受承载体的轴向挤压产生灌浆体局部侧向膨胀，导致灌浆体局部侧摩阻力提高，从而能分担的荷载增加，故受拉锚固段分担荷载有所降低，使得受拉承载系数计算值小于受拉长度系数。

4.2   受拉锚固段和承压锚固段分担荷载

图 10绘制了不同荷载下，受拉锚固段与承压锚固段分担荷载的实测值与计算值对比图，整体看数值模拟结果与实测结果吻合良好，尤其破坏前的分担荷载规律较为一致，实测和数值模拟的承压锚固段与受拉锚固段协同承载规律基本一致。

图  10  不同荷载作用下受拉和承压锚固段分担荷载

Figure  10.  Load distribution of tension anchorage segment and compression anchorage segment under different loads

下载: 全尺寸图片 幻灯片

TC21型锚杆在接近破坏时，实测承压锚固段分担荷载明显增加，受拉锚固段分担荷载显著减小，判断为受拉锚固段与承压锚固段先后破坏，二者非协同破坏。而模拟结果为，受拉锚固段和承压锚固段分担的荷载都随着张拉荷载的增加而继续增加，判断为受拉锚固段与承压锚固段同时破坏，二者协同破坏。

TC11型锚杆在张拉至40 kN前，承压锚固段分担荷载均多于受拉锚固段，40 kN后两者分担荷载才趋于稳定，且更接近。破坏后，实测的受拉锚固段和承压锚固段分担荷载都随张拉荷载的增加而继续同步增加，判断为受拉锚固段和承压锚固段同时破坏，二者协同破坏。而模拟结果在拉力为70，80kN时，承压锚固段分担荷载分别为39.3，44.8 kN，受拉锚固段分担荷载分别为30.6，35.2 kN，均随拉力同步增加，判断为受拉锚固段与承压锚固段协同破坏。

TC12型锚杆张拉荷载超过90 kN接近破坏时，实测承压锚固段分担荷载降低，受拉锚固段分担荷载明显增加，判断受压锚固段先于受拉锚固段破坏，二者为非协同破坏。数值模拟结果表明拉力为90，100 kN时，受拉锚固段分担荷载为25.1，27.9 kN，承压锚固段分担荷载为64.8，72.1 kN，近似同比增加，判断为受拉锚固段与承压锚固段同步破坏，二者为协同破坏。

承压锚固段和受拉锚固段分担荷载在破坏前反应了二者协同承载规律，在接近破坏时反应了增量荷载的转移。因此，当承压锚固段和受拉锚固段分担荷载规律在极限承载力荷载级及其前一级与接近后一级（破坏）较为一致时，判断是否协同破坏最为准确。而单独通过破坏前、破坏时、破坏后的分担荷载判断协同承载有可能造成一定的偏差，但不影响破坏前的协同承载规律。

5.   结论

本文针对拉压复合型锚杆现场试验，对其荷载传递机理进行了数值模拟，得到4点主要结论。

（1）拉压复合型锚杆极限抗拔承载力显著高于传统全黏结型与压力型锚杆，拉压复合型锚杆承压锚固段筋体轴力等于张拉力，在受拉锚固段处筋体轴力大幅降低，并沿受拉锚固段深度方向递减，破坏时的受拉承载系数略低于受拉长度系数。

（2）拉压复合型锚杆承压锚固段和受拉锚固段的灌浆体轴向应力在承载体两侧反向分布，并随着荷载的增加而不断增大。承压锚固段灌浆体上轴向压应力在承载体处最大，向锚头方向递减；受拉锚固段灌浆体轴向拉应力为先增大后减小。

（3）拉压复合型锚杆承压锚固段灌浆体上轴向压应力显著低于压力型锚杆，受拉锚固段灌浆体上轴向拉应力显著低于全黏结型锚杆。通过优化拉压长度比，可以进一步大幅调控并减小受拉锚固段灌浆体上的轴向拉应力。

（4）拉压复合型锚杆在锚固段界面剪应力随着荷载的增加而增大，在承载体附近的界面剪应力最大，然后向两侧传递并逐渐减小，整体呈“中间大，两端小”的分布规律。在相同拉力下，拉压复合型锚杆浆土界面剪应力显著小于传统全黏结型锚杆与压力型锚杆，且沿锚固段分布更加均匀。