Influences of constitutive model for rockfill materials on calculated stress and deformation of concrete-faced dams
-
摘要: 堆石料本构模型选择是影响混凝土面板坝应力变形计算结果的主要因素。以某典型面板坝为例,采用邓肯E-B非线性弹性模型和“南水”双屈服面弹塑性模型,对坝体填筑过程和蓄水过程进行了三维有限元模拟;研究了两种模型计算的坝体和面板的位移和应力分布差异;分析了两种模型计算结果呈现差异的原因。两种模型计算结果最显著的差异体现在两个方面:①“南水”模型计算的坝体沉降、面板挠度等位移指标小于E-B模型,其原因是“南水”模型计算的坝体小主应力和变形模量更高。②E-B模型计算结果显示蓄水后面板底部顺坡向受拉;而“南水”模型计算的面板顺坡向应力为全断面受压。前者是由E-B模型的各向同性弹性本质决定的,垫层料因水压力作用顺坡向膨胀,产生沿坡面向上的位移;后者是其F1屈服面持续扩张产生塑性体积收缩导致的,塑性体缩抵消了顺坡向弹性膨胀,使垫层料产生沿坡面向下的位移。Abstract: Choice of constitutive model for rockfill materials is the most influencing factor that affects the computed stress and deformation results of concrete-faced dams (CFD). In this study, the Duncan's E-B (EB) nonlinear elastic model and the Nanshui (NS) double-yield surface elastoplastic model are used for rockfill materials to simulate the construction and impounding processes of a typical CFD by using three-dimensional finite element method. The differences in the displacement and stress of rockfill zones and concrete slabs are compared, and the reasons were analyzed. Two most important differences are found. First, the displacement quantities such as the dam settlement and slab deflection predicted by the NS model are smaller than those obtained by the EB model, and this difference can be attributed to the higher minor principal stresses and therefore higher deformation moduli within rockfill zones by the former. Second, the EB model predicts a tensile zone along the upstream slope near the bottom of face slabs, while the results by the NS model shows that the slope stresses of face slabs are completely compressive. The tensile stress predicted by the EB model is due to its isotropic elasticity nature, i.e., the cushion materials expand along the slope under the huge hydrostatic pressure, leading to a displacement upward towards the dam crest. The NS model, on the other hand, predicts an additional plastic volume contraction within the upstream rockfill zones due to the expansion of F1 yield surface, which completely counteracts the elastic expansion along the slope and results in a downward displacement of the cushion layer.
-
Keywords:
- concrete-faced dam /
- rockfill material /
- constitutive model /
- stress and deformation
-
0. 引言
混凝土面板、趾板及其分缝止水共同构成面板坝的防渗体系,其应力变形性状是影响工程安全的关键,但决定性因素是坝体堆石料的应力变形特性。中国电力行业《混凝土面板堆石坝设计规范》要求:对于一级坝、二级高坝和利用软岩料填筑的中坝,应采用三维有限元法进行应力和变形计算分析;对于坝高200 m以上的特高坝,应采用非线性弹性模型、弹塑性模型等两种以上坝料本构模型开展对比分析[1]。
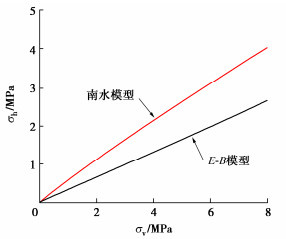
近年来,国内外堆石料本构模型研究成果丰硕[2-5],特别是在剪胀剪缩[2]、颗粒破碎[3]、湿化流变[4]和动力特性[5]模拟等方面取得长足进展。但因配套试验技术、参数取值方法以及实际使用经验等原因,中国坝工界运用较广的模型仍属邓肯E-B非线性弹性模型[6]和“南水”双屈服面弹塑性模型[7]。两者均基于常规三轴试验建立,并假定恒定围压下,偏应力(σ1−σ3)与轴向应变ε1之间符合双曲线假定,由此给出切线弹性模量Et表达式为
Et:=dσ1dε1=(1−Rf⋅SL)2⋅k⋅pa⋅(σ3pa)n。 (1) 式中:Rf为破坏比;pa为大气压力;σ1为大主应力;σ3为小主应力;k和n为初始模量参数;SL为应力水平,由应力状态确定,即
SL=(σ1−σ3)(1−sinφ)2σ3sinφ+2ccosφ。 (2) 式中:c和φ分别为土的黏聚力和内摩擦角。对于堆石料,常采用非线性强度指标,即令c = 0,峰值摩擦角φ随围压增加而降低,即
φ=φ0−Δφlg(σ3pa)。 (3) 式中:φ0和Δφ由不同围压的常规三轴试验确定。
邓肯E-B模型和“南水”模型的不同之处在于体变的模拟。E-B模型假定堆石料切线体积模量Bt随围压增加而增大,但与应力水平无关,即
Bt=kb⋅pa⋅(σ3pa)m。 (4) 式中:kb和m为体积模量参数。不同围压下的切线体积模量由三轴排水试验的应力应变曲线和体变曲线根据一定的原则确定[1, 8]。
“南水”模型则假定恒定围压下土的体积应变εv与轴向应变ε1之间符合抛物线假定[7],由此可得出所谓的切线体积比μt表达式,即
μt:=dεvdε1=2⋅cd(σ3pa)nd⋅1−RdRd⋅ Rf⋅SL⋅Eiσ1−σ3⋅(1−1−RdRdRf⋅SL1−Rf⋅SL)。 (5) 式中:cd,nd,Rd为参数;Ei为初始模量,即Ei = k·pa·(σ3/ pa)n。
邓肯E-B模型和“南水”模型的另一不同之处是加卸载准则,E-B模型常假定当应力增量同时满足以下条件时[9],材料处于卸载状态
σ1−σ3<(σ1 ,SL<(SL 。} (6) 式中:(σ1−σ3)max为历史最大偏应力;(SL)max为历史最大应力水平。试验研究表明:给定围压时,材料卸载回弹模量Ee仅与围压有关,与卸载时的应力水平无关[10],故为减少参数,常采用下面的表达式
{E_{\text{e}}} = {k_{\text{e}}} \cdot {p_{\text{a}}} \cdot {\left( {\frac{{{\sigma _3}}}{{{p_{\text{a}}}}}} \right)^n} 。 (7) 式中:ke为回弹模量参数,一般取为2k~3k;n取值与式(1)中一致。
“南水”模型判断材料加卸载状态是通过引入两个不同的屈服函数实现的,即
\begin{array}{l}{F}_{1}={p}^{2}+{r}^{2}{q}^{2}\text{ }\text{,}\\ {F}_{2}=\frac{{q}^{s}}{p}\text{ }。\end{array}\} (8) 式中:p和q分别为平均应力和八面体剪应力;r和s是模型常数,一般取r = s = 2。当应力增量使F1和F2均超过其历史最大值时,材料处于弹塑性加载状态,其柔度矩阵由弹性部分、与F1相应的塑性部分、与F2相应的塑性部分组成;当应力增量使F1和F2均低于其历史最大值时,材料处于回弹状态,柔度矩阵仅含弹性部分;否则应根据应力增量和屈服函数历史极值确定与各屈服函数相应的塑性柔度矩阵贡献[9]。无论处于何种加卸载状态,“南水”模型的弹性柔度矩阵均由式(7)给出的弹性模量和弹性泊松比ve确定,其中,弹性泊松比一般可取0.3左右。
对于面板堆石坝,邓肯E-B模型和“南水”模型计算结果的差异性已取得初步认识[11-12]:E-B模型计算的坝体沉降、水平位移、面板挠度均高于“南水”模型;E-B模型计算的面板轴向和顺坡向拉应力范围和量值均大于“南水”模型。但是,对两种模型计算结果呈现这种差异性的根本原因尚未深入分析,大多仅归结于“南水”模型可以合理反映堆石料的剪胀剪缩特性这一必然结论。
本文以某典型面板堆石坝为例,基于堆石料试验结果确定邓肯E-B模型和“南水”模型计算参数,并采用两种模型对大坝填筑和蓄水过程进行模拟,分析堆石坝体和混凝土面板应力变形差异,并从本构模型角度揭示产生差异性的本质原因,为判断计算结果合理性以及本构模型完善和参数选择等提供基本依据。
1. 工程概况与计算模型
1.1 材料分区与加载过程
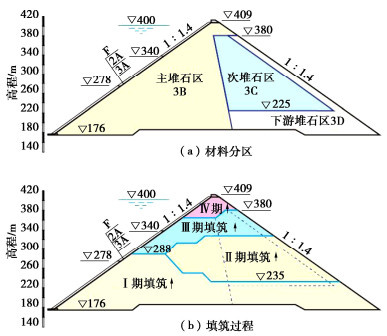
本文面板坝案例最大坝高230余米,从上游至下游主要有5个材料分区,即垫层区(2A)、过渡区(3A)、主堆石区(3B)、次堆石区(3C)以及下游堆石区(3D),如图 1所示。大坝填筑主要分四期(图 1):一期临时断面抢筑至288 m高程,其后浇筑一期面板至278 m高程;二期、三期坝体填筑至360 m高程后,浇筑二期面板至340 m高程;其后,填筑四期坝体至405 m高程,浇筑三期面板至405 m高程;最后完成防浪墙和坝顶409 m高程以下填筑。大坝填筑过程中,曾用临时断面挡水度汛;面板施工前,也曾为堆石体预留沉降期,加卸载和流变过程较为复杂。
为使计算结果的影响因素尽可能少,本文计算模拟时对上述过程进行了适当简化:堆石料仍按照图 1所示的4个分期填筑;然后从底至顶一次浇筑面板至405 m高程;最后水库水位由176 m逐渐提升至400 m高程。
1.2 大坝有限元模型
根据坝体施工过程和面板分缝情况建立了大坝三维有限元模型,如图 2所示。面板和垫层料之间设置摩擦接触单元;面板和趾板之间设置周边缝单元;面板和面板之间设置垂直缝单元,以模拟不同材料和不同结构之间的荷载传递机制。接触单元和缝单元均采用文献[13]中的模型与参数。模型的左右岸截断边界设置坝轴向(x向)位移约束;坝体与建基面接触的结点设置为三向约束。
1.3 本构模型参数
本文研究目的不是重现该面板坝监测结果,而是探究两种经典模型计算结果差异的原因。因此,采用笔者实验室两种典型堆石料(堆石料A和堆石料B)试验结果确定本构模型参数,如表 1所列,其中:前6列是E-B模型和“南水”模型的共同参数;第7列和第8列是E-B模型体变参数;最后3列是“南水”模型体变参数。计算时垫层料、过渡料、主堆石料和下游堆石料均采用堆石料A参数;次堆石料采用堆石料B参数。
表 1 筑坝堆石料本构模型参数Table 1. Constitutive model parameters of damming rockfill materials材料 ρ/ (g·cm-3) φ0/
(°)Δφ/
(°)Rf k n kb m cd/
%nd Rd 堆石料A 2.20 54.3 9.8 0.61 1230 0.26 611 0.12 0.28 0.77 0.55 堆石料B 2.20 52.3 8.0 0.61 892 0.33 351 0.27 0.52 0.59 0.57 对于混凝土趾板和面板,本文采用各向同性线弹性模型模拟,弹性模量为E = 28 GPa;弹性泊松比为v = 0.167。
2. 堆石坝体应力变形差异分析
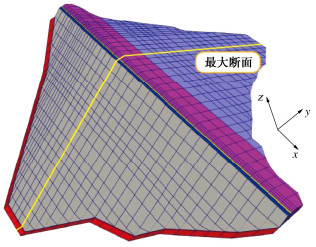
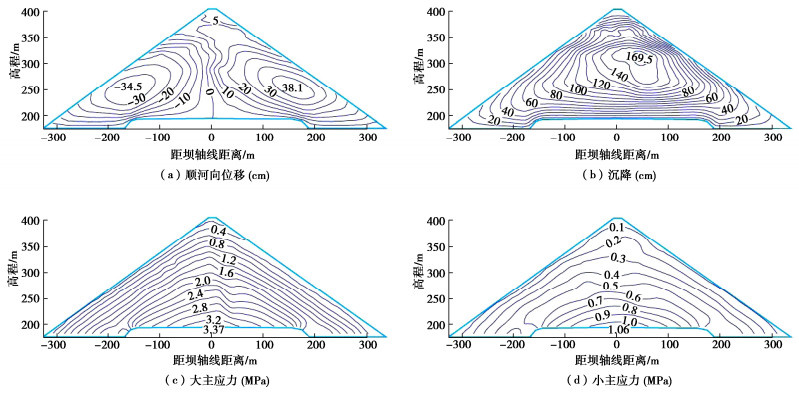
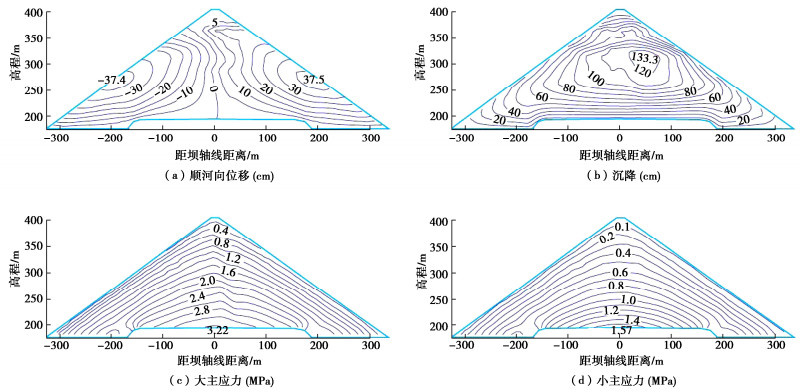
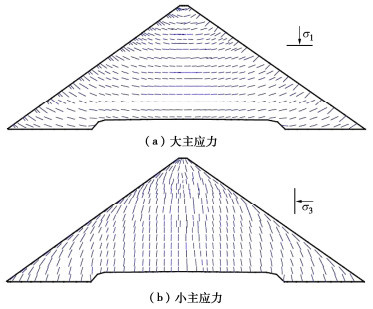
图 3,4中分别绘制了填筑竣工时由两种模型计算得到的河床最大剖面堆石体位移和应力分布等值线。在该案例中,坝体水平位移和大主应力计算结果基本一致;但两种模型计算的坝体沉降和小主应力分布差异较大:“南水”模型计算的坝体沉降明显低于E-B模型,仅为前者的78%左右;而在同高程部位,“南水”模型的小主应力明显高于E-B模型。对于大多数面板坝,最大沉降发生的河床最大断面大体处于平面应变状态,竖直方向是堆石体大主应力方向;坝轴向是中主应力方向;顺河向是小主应力方向,如图 5所示。因此,填筑过程是从大主应力方向施加荷载,与三轴压缩试验的加载方向基本吻合。“南水”模型计算沉降小于E-B模型的直接原因是前者计算的坝体小主应力较大,在基本相同的大主应力条件下,应力水平较低,故由式(1)计算的竖直向加载切线模量较高,在相同的竖向荷载作用下变形较小。但需解释的是,为何“南水”模型会计算出更高的小主应力?
大坝填筑的竖直向加载过程产生水平应力增量的原因是坝体受到两岸河谷和坝基的约束,因此,需要考察侧限条件下两种模型模拟堆石料应力应变特性方面的差异。图 6给出了堆石料A和堆石料B在单向压缩过程中孔隙比e随竖向应力σv的变化过程。对于E-B模型,其应力驱动(柔度形式)的本构方程为
\left( {\begin{array}{*{20}{c}} {{\text{d}}{\varepsilon _1}} \\ {{\text{d}}{\varepsilon _2}} \\ {{\text{d}}{\varepsilon _3}} \end{array}} \right) = \frac{1}{{{E_{\text{t}}}}}\left[ {\begin{array}{*{20}{c}} 1&{ - {v_{\text{t}}}}&{ - {v_{\text{t}}}} \\ { - {v_{\text{t}}}}&1&{ - {v_{\text{t}}}} \\ { - {v_{\text{t}}}}&{ - {v_{\text{t}}}}&1 \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{\text{d}}{\sigma _1}} \\ {{\text{d}}{\sigma _2}} \\ {{\text{d}}{\sigma _3}} \end{array}} \right) 。 (9) 式中:vt为切线泊松比,可由切线弹性模量和切线体积模量按下式计算[9]
{v_{\text{t}}} = \frac{1}{2} - \frac{{{E_{\text{t}}}}}{{6{B_{\text{t}}}}} 。 (10) 单向压缩试验中,侧向应变dε2 = dε3 = 0,故由式(9)可得
\left.\begin{array}{l} \frac{\mathrm{d} \sigma_3}{\mathrm{~d} \sigma_1}=\frac{v_{\mathrm{t}}}{1-v_{\mathrm{t}}}, \\ \mathrm{~d} \varepsilon_1=\frac{1}{E_{\mathrm{t}}} \frac{\left(1-2 v_{\mathrm{t}}\right)\left(1+v_{\mathrm{t}}\right)}{1-v_{\mathrm{t}}} \mathrm{~d} \sigma_1。 \end{array}\right\} (11) 对于“南水”模型,其主应力空间的本构方程可以表示为
{\text{d}}{\mathbf{\varepsilon }} = {{\mathbf{C}}_{\text{e}}} \cdot {\text{d}}{\mathbf{\sigma }} + \frac{1}{{{H_1}}}\left( {\frac{{\partial {F_1}}}{{\partial {\mathbf{\sigma }}}}} \right){\text{d}}{F_1} + \frac{1}{{{H_2}}}\left( {\frac{{\partial {F_2}}}{{\partial {\mathbf{\sigma }}}}} \right){\text{d}}{F_2} 。 (12) 式中:Ce为弹性柔度矩阵,其形式与式(9)中一致,只需将切线弹性模量和切线泊松比替换成弹性模量Ee和弹性泊松比ve即可;H1和H2分别为与两个屈服函数对应的塑性模量参量[7]。利用侧向应变为零的条件,可以得出主应力增量之间的关系,即
\frac{{{\text{d}}{\sigma _3}}}{{{\text{d}}{\sigma _1}}} = \frac{{\frac{{{v_{\text{e}}}}}{{{E_{\text{e}}}}} - \frac{1}{{{H_1}}}\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}\frac{{\partial {F_1}}}{{\partial {\sigma _1}}} - \frac{1}{{{H_2}}}\frac{{\partial {F_2}}}{{\partial {\sigma _3}}}\frac{{\partial {F_2}}}{{\partial {\sigma _1}}}}}{{\frac{{1 - {v_{\text{e}}}}}{{{E_{\text{e}}}}} + \frac{2}{{{H_1}}}\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}\frac{{\partial {F_1}}}{{\partial {\sigma _3}}} + \frac{2}{{{H_2}}}\frac{{\partial {F_2}}}{{\partial {\sigma _3}}}\frac{{\partial {F_2}}}{{\partial {\sigma _3}}}}} 。 (13) 这样就可以得到竖向应力施加过程中,侧向应力的增长过程,进而求出应变发展过程。
图 6对比了两种模型模拟单向压缩试验的结果;图 7则给出了两种模型预测的应力路径。从图 6可以看出,E-B模型高估了侧限条件下堆石料的压缩变形,特别是堆石料B;“南水”模型模拟结果与试验结果吻合度更高,尽管该模型所有参数也是基于常规三轴试验结果确定的。
图 7中所绘制的应力路径实际上给出了堆石料A的静止土压力系数K0,根据E-B模型计算结果,两种堆石料的K0值在0.34左右;“南水”模型计算的K0值则达到0.5左右。图 3和图 4中两种模型计算的坝轴线底部小主应力与大主应力之比分别为0.31和0.49,略低于上述K0值,系因模型底部并非严格的侧限条件。两种模型K0值的上述差异必然导致坝体内水平应力差异,进而导致变形模量和沉降差异。由于缺乏两种堆石料K0实测结果,目前无法判断上述预测结果合理性,但由式(11)可知,E-B模型K0计算结果已由切线弹性模量和切线体积模量参数完全确定;而由式(13)可知,“南水”模型尚具有通过调整两个弹性参数(即ke和ve),拟合K0值和单向压缩试验结果的灵活性。有条件时应开展测定水平应力的单向压缩试验,确定堆石料弹性模量和泊松比参数,因为按常规取值经验(如本文取ke=2k;ve=0.3)并不总能良好模拟堆石料压缩变形特性,如图 6(b)所示。
3. 面板应力变形差异分析
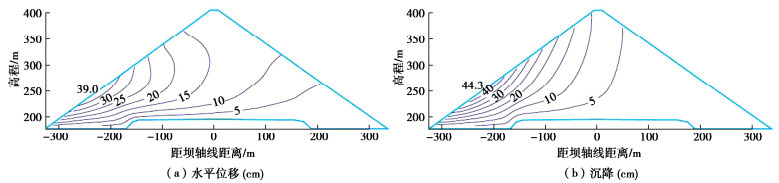
图 8,9分别给出了用E-B模型和“南水”模型计算的蓄水期面板位移和应力结果,两种模型计算的面板位移分布规律基本一致,但量值上存在差异:E-B模型计算的面板轴向位移值略大于“南水”模型计算值;而前者计算的面板挠度远大于后者。由于位移分布差异,E-B模型计算的面板轴向拉压应力值略大于“南水”模型计算值,压应力极值位于河床断面的面板中下部;拉应力区主要分布在两岸坡部位面板中。值得注意的是,两种模型计算的面板顺坡向应力存在定性差异,“南水”模型计算结果表明面板顺坡向处于全断面受压状态,而E-B模型计算结果显示,河床断面和两岸陡峻岸坡部位的面板底部处于受拉状态。在本案例中,面板是蓄水前一次浇筑完成的,自重作用下两种模型计算的面板应力分布基本一致,因此可以推断,蓄水引起的面板应力增量存在较明显的差异。
水压力作用下面板应力变化是由面板与垫层接触面传递的摩擦力决定的,因此,可考察蓄水引起的垫层表面位移增量,如图 10,11所示。水压力作用下,两岸垫层均向河谷中央位移,E-B模型计算的轴向位移大于“南水”模型,与面板位移分布规律的差异性一致。两种模型计算的垫层料顺坡向位移增量存在显著不同:E-B模型计算结果表明,水压力使垫层料产生沿坝坡指向坝顶的位移增量;南水模型计算结果则显示垫层料产生沿坝坡指向坝底的位移。
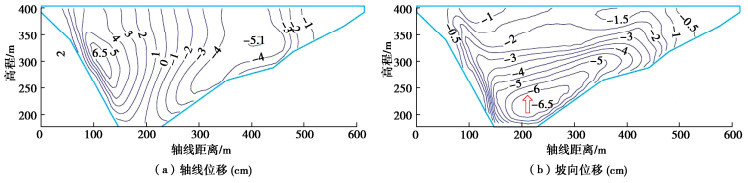
上述垫层位移分布差异是两种模型计算的坝体水平位移增量与沉降增量的不同比例关系决定的。图 12,13给出了两种模型计算的蓄水引起的堆石坝体水平位移增量和沉降增量等值线,E-B模型计算的位移量值明显大于“南水”模型,但更重要的差异体现在位移比值上,如图 14所示。E-B模型计算的坝体内沉降增量普遍小于水平位移增量,仅在垫层表面附近沉降增量与水平位移增量之比大于1,但比值始终小于坝坡坡比,故合成的位移矢量沿坡面向上,从而使面板底部处于受拉状态;“南水”模型计算的坝体位移增量比几乎处处大于1,蓄水引起坝体变形由沉降占主导,特别是在垫层表面附近,位移增量比从坝底部位的1.4左右逐渐增大至坝顶部位的3.0以上,因此垫层表面合成的位移矢量沿坡面向下,从而使面板受到向下的摩擦力作用,在低高程部位产生比较大的顺坡向压应力。
图 15中进一步绘制了两种模型计算的堆石坝体顺坡向应变增量等值线,E-B模型计算结果表明蓄水使垫层底部产生拉应变;底部以上范围产生压应变,两者的分界处即图 12中最大坡向位移所在点。“南水”模型计算结果截然相反,垫层顶部产生拉应变区;其下是压应变区,两者分界也位于最大坡向位移处。E-B模型预测的量值占优的顺坡向拉应变具有增大水平位移、减小沉降的作用,从而对应较小的位移增量比;相反,“南水”模型预测的量值占优的顺坡向压应变具有增大沉降、减小水平位移的作用,从而对应较大的位移增量比。因此,上述位移分布模式的差异归根到底是为什么水压力作用下会产生图 15所示的顺坡向应变增量分布?
为回答上述问题,首先来看两种模型预测的蓄水过程加载区分布,如图 16~18所示。对于E-B模型,其加载区系指不满足卸载准则关系式(6)的区域;对于“南水”模型,其加载区则根据屈服函数当前值及其历史极值判别。对比图 15,16可以看出,E-B模型计算的顺坡向拉应变高值区与加载区基本一致,但除下游坝脚区一定范围内始终处于加载状态外,大部分加载区在蓄水过程中都经历过一定阶段的卸载。图 19给出了坝体内3个典型单元泊松比随水位的变化过程。由于水压力作用方向与单元小主应力方向接近,施加水压力时各单元均经历偏应力和应力水平降低的卸载阶段,其切线泊松比由下式给出[14]
{v_{\text{t}}} = \frac{1}{2} - \frac{{{k_{\text{e}}}}}{{6{k_{\text{b}}}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\text{a}}}}}} \right)^{n - m}} 。 (14) 利用表 1中参数可验证,上式给出的卸载泊松比在小主应力很小的情况下就出现负值。因此,蓄水过程模拟时,堆石料泊松比在再加载前是由计算软件设定的下限值(本文取0.01)确定的,而非小主应力方向加载时材料的真实力学参数。值得说明的是,采用泊松比下限值计算是出于使计算顺利进行的考虑,但它一定程度上符合堆石料从小主应力方向加载时的侧向变形特性。真三轴试验结果表明:对于砂土、堆石料等无黏性土,从小主应力方向加载时大主应力方向的侧向膨胀量远小于从大主应力方向加载时小主应力方向的侧向膨胀量[15]。
当水位达到一定高度后,处于卸载状态的单元将重新进入加载状态,此时的切线泊松比vt表示为[14]
{v_{\text{t}}} = \frac{1}{2} - {\left( {1 - {R_{\text{f}}} \cdot {S_{\text{L}}}} \right)^2}\frac{k}{{6{k_{\text{b}}}}}{\left( {\frac{{{\sigma _3}}}{{{p_{\text{a}}}}}} \right)^{n - m}} 。 (15) 显然加卸载变化的瞬间,泊松比会出现非连续变化,如图 19所示,这种变形特性突变是该模型理论上的一个不足,因为连续荷载作用下堆石料的变形特性应是连续的。
图 15中E-B模型计算的坝体顺坡向拉应变分布是由其各向同性弹性本质决定的。水压力作用于垫层表面;因无顺坡向荷载增量,故顺坡向正应力几乎保持不变;坝轴向正应力则因堆石体向河谷中央挤压而增大,因此,堆石坝体必然顺坡向膨胀,但底部受到边界约束,故只能产生沿坝坡向上的位移。这种位移在较高高程部位受到两岸坝体约束,故在顶部产生压应变区(图 15)。而在低高程部位,因承受的水压力较大,且更早进入再加载阶段,故顺坡向膨胀量较大,使得底部面板产生较大的拉应力,抵消了蓄水前自重作用下面板底部的压应力。
对于“南水”模型,其应变分布的显著特点是在上游坝脚部位出现量值可观的顺坡向压应变区,如图 15所示,这可从坝体加载区分布与变化过程得到定性解释:蓄水过程中,水位以下堆石体不仅因平均应力增加而产生弹性体积收缩,还始终产生因F1屈服扩张导致的塑性体积收缩(图 17),且整个蓄水过程中,坝轴线上游侧堆石体几乎不产生因F2屈服扩张导致的塑性体积膨胀(图 18)。图 20给出了蓄水过程中3个典型单元的顺坡向应变和轴向、顺坡向、法向正应力发展过程,其中法向应力即垂直面板方向的正应力。
欲进一步解释图 15中“南水”模型预测的坝体顺坡向压应变结果,不妨从模型柔度矩阵着手,根据图 17,18中加载区分布,蓄水过程中坝轴线上游侧材料的本构方程仅含式(12)右侧前两项。因此,主应力空间中,塑性柔度矩阵Cp可表示为
{{\mathbf{C}}_{\text{p}}} = \frac{1}{{{H_1}}}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {F_1}}}{{\partial {\sigma _1}}}\frac{{\partial {F_1}}}{{\partial {\sigma _1}}}}&{\frac{{\partial {F_1}}}{{\partial {\sigma _1}}}\frac{{\partial {F_1}}}{{\partial {\sigma _2}}}}&{\frac{{\partial {F_1}}}{{\partial {\sigma _1}}}\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}} \\ {\frac{{\partial {F_1}}}{{\partial {\sigma _2}}}\frac{{\partial {F_1}}}{{\partial {\sigma _1}}}}&{\frac{{\partial {F_1}}}{{\partial {\sigma _2}}}\frac{{\partial {F_1}}}{{\partial {\sigma _2}}}}&{\frac{{\partial {F_1}}}{{\partial {\sigma _2}}}\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}} \\ {\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}\frac{{\partial {F_1}}}{{\partial {\sigma _1}}}}&{\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}\frac{{\partial {F_1}}}{{\partial {\sigma _2}}}}&{\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}\frac{{\partial {F_1}}}{{\partial {\sigma _3}}}} \end{array}} \right] 。 (16) 式中:塑性模量参量H1 > 0。根据屈服函数F1表达式,易得
\left.\begin{array}{l} \frac{\partial F_1}{\partial \sigma_1}=\frac{2}{3}\left[p+r^2\left(\sigma_1-p\right)\right] ,\\ \frac{\partial F_1}{\partial \sigma_2}=\frac{2}{3}\left[p+r^2\left(\sigma_2-p\right)\right] ,\\ \frac{\partial F_1}{\partial \sigma_3}=\frac{2}{3}\left[p+r^2\left(\sigma_3-p\right)\right]。 \end{array}\right\} (17) 因此,塑性柔度矩阵的主对角元必为正值,与弹性柔度矩阵一致;但塑性柔度矩阵非对角线元可正可负,取决于3个应力分量的相对大小,与弹性柔度矩阵非对角元恒定为负不同。现设
{\sigma _2} = {c_2} \cdot {\sigma _1},\quad {\sigma _3} = {c_3} \cdot {\sigma _1} 。 (18) 将式(20)代入式(19),可得
\left.\begin{array}{l} \frac{\partial F_1}{\partial \sigma_1}=\left[\frac{1+c_2+c_3}{3}+r^2\left(1-\frac{1+c_2+c_3}{3}\right)\right] \sigma_1, \\ \frac{\partial F_1}{\partial \sigma_2}=\left[\frac{1+c_2+c_3}{3}+r^2\left(c_2-\frac{1+c_2+c_3}{3}\right)\right] \sigma_1, \\ \frac{\partial F_1}{\partial \sigma_3}=\left[\frac{1+c_2+c_3}{3}+r^2\left(c_3-\frac{1+c_2+c_3}{3}\right)\right] \sigma_1。 \end{array}\right\} (19) 上述关系式实际上适用于任何3个正交方向的正应力(变)场。现将水压力作用方向定义为方向1;坝轴向定义为方向2;顺坡向定义为方向3,则根据图 20中各单元应力路径可得塑性柔度矩阵非对角元的正负值变化情况,如图 21所示。对于单元E1和E3,水库水位超过250 m后,法向应力迅速增加,柔度矩阵元素C13恒定为正值;对于单元E2,水库水位超过300 m后,法向应力迅速增加,柔度矩阵元素C13也恒定为正值,也就是说法向应力增量引起顺坡向收缩,直至最高库水位。本文中,堆石料弹性泊松比取0.3,与邓肯E-B模型计算的泊松比接近(≈ 0.25),因此两种模型弹性膨胀率大体相当,但在“南水”模型中,上游堆石体顺坡向弹性膨胀被塑性压缩所抵消,从而产生顺坡向压应变。
4. 结论
本文以某200 m级面板坝为例,基于两种典型堆石料的邓肯E-B模型参数和“南水”模型参数,研究了两种本构模型计算的堆石坝体和混凝土面板应力变形差异,并分析了产生差异的原因,主要得到以下3点结论。
(1)“南水”模型计算的自重引起的坝体沉降以及水压力作用引起的坝体水平位移和沉降均小于E-B模型,其原因是“南水”模型计算的坝体小主应力值和坝体的变形模量高于E-B模型。“南水”模型的主应力比主要受控于其弹性参数,有条件时宜由测定水平应力的单向压缩试验(或测定水平应力的平面应变试验)确定。
(2)“南水”模型和E-B模型计算的垫层顺坡向位移和面板顺坡向应力存在显著差异,前者垫层料沿坡面向坝底位移,面板底部处于受压状态;后者垫层料沿坡面向坝顶位移,底部面板处于受拉状态。造成这种差异的原因是水压力作用下坝体位移增量比值的不同,“南水”模型以沉降占主导,而E-B模型以水平位移占主导。
(3)坝轴线上游侧堆石体是水压力承载的主体,“南水”模型和E-B模型模拟蓄水时,上游坝体均经历卸载和再加载过程,E-B模型因其各向同性弹性本质,坝体产生顺坡向膨胀;“南水”模型因其F1屈服面持续扩张产生塑性体积收缩,抵消了水压力作用下坝体的顺坡向膨胀,使上游坝脚附近处于压缩状态。
-
表 1 筑坝堆石料本构模型参数
Table 1 Constitutive model parameters of damming rockfill materials
材料 ρ/ (g·cm-3) φ0/
(°)Δφ/
(°)Rf k n kb m cd/
%nd Rd 堆石料A 2.20 54.3 9.8 0.61 1230 0.26 611 0.12 0.28 0.77 0.55 堆石料B 2.20 52.3 8.0 0.61 892 0.33 351 0.27 0.52 0.59 0.57 -
[1] 混凝土面板堆石坝设计规范: NB/T 10871—2021E[S]. 北京: 中国水利水电出版社, 2022. Code for Design of Concrete Face Rockfill Dams: NB/T 10871—2021E[S]. Beijing: China Water & Power Press, 2022. (in Chinese)
[2] 程展林, 姜景山, 丁红顺, 等. 粗粒土非线性剪胀模型研究[J]. 岩土工程学报, 2010, 32(3): 460-467. CHENG Zhanlin, JIANG Jingshan, DING Hongshun, et al. Nonlinear dilatancy model for coarse-grained soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 460-467. (in Chinese)
[3] XIAO Y, LIU H L, YANG G. A constitutive model for the state-dependent behaviors of rockfill material considering particle breakage[J]. Science China (Technological Sciences), 2014, 57(8): 1636-1646. doi: 10.1007/s11431-014-5601-6
[4] FU Z Z, CHEN S S, LIU S H. Hypoplastic constitutive modelling of the wetting induced creep of rockfill materials[J]. Science China (Technological Sciences), 2012, 55(7): 2066-2082. doi: 10.1007/s11431-012-4835-4
[5] 孔宪京, 邹德高. 紫坪铺面板堆石坝震害分析与数值模拟[M]. 北京: 科学出版社, 2014. KONG Xianjing, ZOU Degao. Seismic Damage Analysis and Numerical Simulation of Zipingpu Concrete Face Rockfill Dam[M]. Beijing: Science Press, 2014. (in Chinese)
[6] DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of Soil Mechanics and Foundations Division, ASCE, 1970, 96(SM5): 1629-1653.
[7] 沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000. SHEN Zhujiang. Theoretical Soil Mechanics[M]. Beijing: China Water & Power Press, 2000. (in Chinese)
[8] 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for geotechnical testing method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019. (in Chinese)
[9] 殷宗泽. 土工原理[M]. 北京: 中国水利水电出版社, 2007. YIN Zongze. Geotechnical Principle[M]. Beijing: China Water & Power Press, 2007. (in Chinese)
[10] FU Z Z, CHEN S S, PENG C. Modeling cyclic behavior of rockfill materials in a framework of generalized plasticity[J]. International Journal of Geomechanics, ASCE, 2014, 14(2): 191-204. doi: 10.1061/(ASCE)GM.1943-5622.0000302
[11] 方维凤. 混凝土面板堆石坝流变研究[D]. 南京: 河海大学, 2003. FANG Weifeng. Study on Rheology of Concrete Face Rockfill Dam[D]. Nanjing: Hohai University, 2003. (in Chinese)
[12] 王永明, 汝璇卿. 高面板堆石坝工作性态的弹性和弹塑性对比分析[J]. 三峡大学学报(自然科学版), 2009, 31(6): 24-28. doi: 10.3969/j.issn.1672-948X.2009.06.006 WANG Yongming, RU Xuanqing. Comparative analysis of high concrete faced rockfill dam with elastic analysis and elastoplastic analysis methods[J]. Journal of China Three Gorges University (Natural Sciences), 2009, 31(6): 24-28. (in Chinese) doi: 10.3969/j.issn.1672-948X.2009.06.006
[13] 顾淦臣, 束一鸣, 沈长松. 土石坝工程经验与创新[M]. 北京: 中国电力出版社, 2004. GU Ganchen, SHU Yiming, SHEN Changsong. Experience and Innovation of Earth-Rock Dam Engineering[M]. Beijing: China Electric Power Press, 2004. (in Chinese)
[14] 殷宗泽, 张坤勇, 朱俊高. 面板堆石坝应力变形计算中考虑土的各向异性[J]. 水利学报, 2004, 35(11): 22-26, 32. doi: 10.3321/j.issn:0559-9350.2004.11.004 YIN Zongze, ZHANG Kunyong, ZHU Jungao. Computation for stress and deformation of concrete slab inrock-fill dam in consideration of soil anisotropy[J]. Journal of Hydraulic Engineering, 2004, 35(11): 22-26, 32. (in Chinese) doi: 10.3321/j.issn:0559-9350.2004.11.004
[15] 殷宗泽, 徐志伟. 土体的各向异性及近似模拟[J]. 岩土工程学报, 2002, 24(5): 547-551. doi: 10.3321/j.issn:1000-4548.2002.05.001 YIN Zongze, XU Zhiwei. Anisotropy of soils and its approximate simulation[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 547-551. (in Chinese) doi: 10.3321/j.issn:1000-4548.2002.05.001
-
其他相关附件



 下载:
下载: