Influences of different inclination modes on seismic response of inclined liquefiable site
-
摘要: 在倾斜场地地震液化后，土体的侧向流动扩展引起的场地失效以及大变形问题的研究中，不同的倾斜方式会对试验结果产生一定的影响，而目前针对不同倾斜方式对倾斜液化场地土体地震动力响应影响评价的研究成果还较为少见。根据课题组开展的水平液化自由场振动台试验，首先基于OpenSees有限元平台建立了水平液化自由场有限元计算模型，在数值模型中考虑了模型箱对场地土地震响应的影响，通过对比数值计算结果与试验结果验证了数值模型的可靠性。在此基础上建立了倾斜液化自由场有限元计算模型，分别建立了层剪箱整体倾斜模型、层剪箱场地土倾斜模型和刚性箱场地土倾斜3种不同的数值模型来模拟振动台试验中采用的不同的倾斜方式。通过对比，分析了在0.3g汶川地震卧龙波作用下3个数值模型计算得到的自由场土体动力响应结果，并讨论了3种不同的倾斜方式对计算结果的影响，最后给出了针对倾斜液化场地地震动力响应数值模拟和振动台试验研究中的一些有参考价值的结论。Abstract: In the study of the failure and large deformation of inclined site caused by lateral flow expansion of soil after seismic liquefaction, different inclined modes will have a certain impact on the test results, but the research results on the impact evaluation of seismic response of inclined liquefiable site are still relatively rare at present. In this study, a numerical model for horizontal liquefiable field is established based on the OpenSees finite element platform according to the completed shaking table tests, and the influences of the model box on the dynamic response of soil are considered in this numerical model, and the validity of numerical model is verified by comparing with the shaking table test results. Then the finite element numerical model for inclined liquefiable site is established based on the horizontal numerical model, and three different numerical models for inclined shear box model, inclined soil in shear box model and inclined soil in rigid box model are established to simulate different inclination modes in the shaking table tests. Through comparison, the dynamic responses of soil calculated by three numerical models under the action of 0.3g Wenchuan earthquake Wolong wave are examined, and the influences of three different inclination modes on the results are analyzed, and some valuable conclusions about the researches on the numerical simulation and shaking table tests of seismic dynamic response of inclined liquefiable sites are shown.
-
Keywords:
- inclined mode /
- inclined liquefiable soil /
- laminar shear box model /
- rigid box model
-
0. 引言
历次地震震害调查发现，地震过程中饱和砂土液化导致土体发生侧向位移是造成结构物发生破坏的主要原因之一[1]。最初Hamada等[2]在对1964年Niigata地震和1983年Nihonkai-Chubu地震灾害进行调查过程中发现了倾斜砂土层在地震作用下达到液化从而导致土体发生侧向流动的震害案例。此后，土体在地震作用下液化从而引起土体侧向流动的问题引起了国内外学者的关注。2008年中国汶川地震[3]、2010年智利大地震[4]、2018年印度尼西亚Palu地震[5]中均存在砂土液化引起土体侧向流动从而导致结构物发生破坏的现象。
对这些地震震害案例进行总结发现，大量的土体侧扩流现象发生在坡度较小的缓坡场地（微倾场地）中。例如Zhou等[3]对2008年汶川地震中的震害实例进行研究时发现倾斜场地液化引起的侧向位移会产生较大的水平动力荷载，从而导致桥梁等结构发生破坏。Bradley等[5]对2018年印尼Palu地震进行调查，发现倾斜1°的倾斜场地发生了明显的土体侧移现象。受地质成因和地质构造的影响，中国滨海、滨河以及三角洲等地带，地表往往伴随着0°~5°的倾斜坡度。因此研究微倾斜液化场地的地震反应规律对中国处于地震带的近海或河道地基的稳定性是非常必要的。
为了研究倾斜液化场地地震反应规律，国内外学者开展了一系列模型试验。Dobry等[6]使用层剪箱开展倾斜液化自由场振动台模型试验，研究倾斜液化场地在地震荷载作用下场地土体的动力响应问题。Chang等[7]使用层剪箱倾斜方式开展倾斜液化场地单桩动力反应振动台模型试验，研究了单桩在土体侧向位移作用下的地震动力响应；Jia等[8]使用层剪箱整体倾斜方式开展倾斜液化场地群桩动力反应振动台模型试验，主要研究了群桩体系在土体侧扩流作用下的破坏机理。张鑫磊等[9]使用层剪箱场地土倾斜的方式开展可液化场地群桩基础振动台模型试验，研究地震荷载作用下场地土体及桩基结构的反应特征。国内外学者针对倾斜液化场地地震反应规律的研究采用的倾斜方式不尽相同，采用不同的倾斜方式会对试验结果产生一定的影响，而目前针对不同倾斜方式对倾斜液化场地土体地震动力响应影响评价的研究成果还较为少见。
模型试验在很大程度上会受到试验条件的限制，且多次进行类似试验也会造成物资的浪费，采用数值模拟的方法可以降低成本，并且可以针对不同复杂的试验工况进行计算。国内外学者为针对地震作用下场地土体的动力响应问题开展了大量的有限元数值模拟研究。Elgamal等[10]基于OpenSees有限元平台建立了多屈服面塑性本构模型，并利用模型试验数据对模型进行校准，该模型能够较为准确地反映饱和砂土的液化特性。周林禄等[11]对不同的砂土本构模型进行对比，发现其中弹塑性饱和砂土液化本构模型PDMY可以较好地模拟动荷载作用下饱和松砂超孔压的累积效应和剪缩效应。Su等[12]基于OpenSees有限元平台研究土体侧扩流作用下码头桩的地震动力响应问题。
本文基于课题组已开展的水平自由场振动台模型试验，采用OpenSees有限元平台[13]建立倾斜自由场数值模型，分别建立了层剪箱整体倾斜模型、层剪箱场地土倾斜模型以及刚性箱场地土倾斜3个不同的数值模型来模拟倾斜液化场地振动台模型试验中不同的倾斜方式。通过对3个数值模型计算结果进行对比，分析不同的倾斜方式对倾斜自由场土体动力响应的影响。
1. 数值模型验证
依据课题组前期开展的水平液化自由场大型振动台模型试验，基于Boit多孔介质固结理论建立水平自由场数值模型；将数值模拟得到的动力响应结果与振动台模型试验结果对比，从而验证水平自由场数值模型的可靠性。
1.1 振动台模型试验介绍
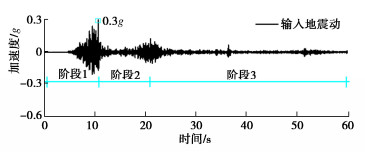
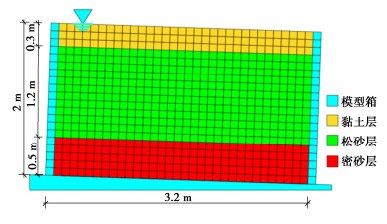
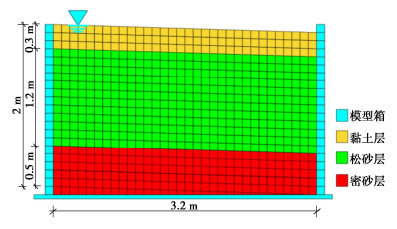
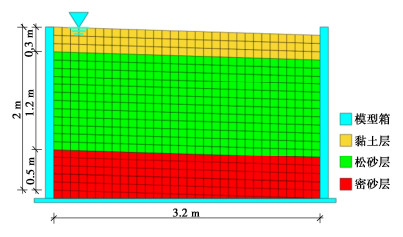
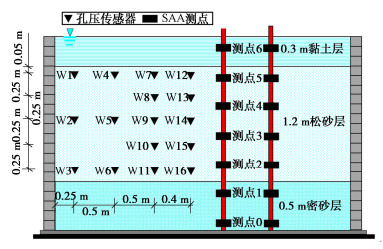
水平液化自由场振动台模型模型试验中采用矩形层状剪切模型箱（简称层剪箱），该模型箱的内尺寸为3.2 m×2.4 m×2.0 m（长×宽×高），土层自下而上分别由0.5 m密砂层、1.2 m饱和松砂层以及0.3 m上覆黏土层构成[14]。水位线保持与上覆黏土层表面齐平，土层分布与传感器布置如图 1所示。试验选用汶川地震卧龙台地震记录作为输入地震动，峰值调整为0.3g，其加速度时程曲线如图 2所示。
![]()
图 1 水平自由场振动台模型试验传感器布置图Figure 1. Layout of sensors for shaking table tests on horizontal free field![]()
图 2 汶川地震卧龙台地震记录加速度时程曲线Figure 2. Time histories of acceleration recorded at Wolong station of Wenchuan earthquake1.2 水平自由场数值模型建立
（1）土体模型
本文数值模型中的饱和砂土本构采用多屈服面塑性本构模型PDMY02（pressure depend multi yield02）进行模拟。数值模型中砂土与黏土的计算参数依据振动台试验条件[14]以及OpenSees官网推荐参数[13]确定，砂土的计算参数见表 1。上覆黏土材料采用PIMY（pressure independ multi yield），上覆黏土的具体计算参数见表 2。
表 1 饱和砂土模型参数Table 1. Parameters of saturated sand model参数 密砂层 饱和松砂层 密度ρ/(kg·m-3) 1900 1700 参考剪切模量Gr/kPa 70000 60000 参考体积模量Br/kPa 190000 160000 摩擦角ϕ 33.5 31 峰值剪应变γmax 0.1 0.1 参考围压p/kPa 101 101 压力系数n 0.5 0.5 剪胀角ϕPT 25.5 31 剪缩参数c1 0.045 0.087 剪缩参数c3 0.15 0.21 剪胀参数d1 0.06 0 剪胀参数d3 0.15 0 屈服面数 20 20 初始孔隙比e 0.7 0.85 标准大气压常量/kPa 101 101 表 2 上覆黏土模型参数Table 2. Parameters of overlaid clay model参数 黏土层 质量密度ρ/(kg·m-3) 1300 参考剪切模量Gr/kPa 13000 参考体积模量Br/kPa 65000 黏聚力c/kPa 18 峰值剪应变γmax 0.1 参考围压p/kPa 100 压力系数n 0 屈服面数 20 摩擦角ϕ 0 （2）模型箱模型
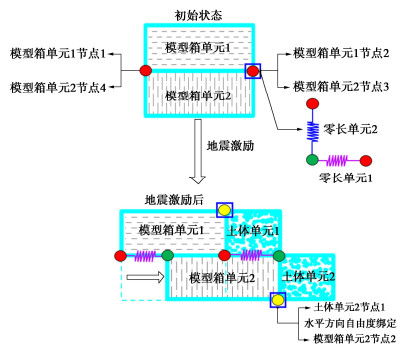
本文研究不同的模型箱倾斜方式对倾斜液化场地土体动力响应的影响，因此在建模过程中考虑了模型箱的影响，模型箱侧壁材料采用弹性各向同性材料，弹性模量取值为2.1×108 kPa，密度取值为2.4×103 kg/m3，泊松比为0.3；模型箱底座材料的弹性模量取值为2.1×108 kPa，密度取值为7.85×103 kg/m3，泊松比取0.3。侧壁与底座均采用四节点四边形单元Quad Element进行模拟，每层模型箱单元之间用零长单元ZeroLength Element连接，零长单元材料均采用弹性各向同性材料Elastic Isotropic，竖直方向上零长单元的弹性模量设为2.1×108 kPa，水平方向上不考虑层间摩擦将零长单元的弹性模量设为0；模型箱单元与土体单元相邻节点的x（水平方向）自由度绑定，模型箱单元与土体单元相邻节点的y（竖直方向）自由度不设约束。层状剪切模型箱模型工作原理如图 3所示。
（3）边界条件及分析步骤
本文建立的水平自由场有限元计算模型的边界条件设置如下：
a）土体底部边界设置为不透水的固定边界，固定模型箱底座节点水平方向和竖直方向的自由度，并将土体底部节点水平方向和竖直方向的自由度与其进行绑定。
b）土体侧向边界均设置不透水周期性边界，使用OpenSees中的EqualDOF命令将土体两侧同一高度的模型箱节点水平方向自由度绑定，以模拟模型箱的实际运动情况，将模型箱单元与土体单元相邻节点的x（水平方向）自由度绑定，以模拟模型箱与土体共同运动。
c）土体顶部边界设置为自由透水边界，约束土体孔压自由度。
有限元分析步骤如下所示：
a）进行重力分析，将饱和土层的渗透系数设为1，以实现土体的快速固结。对土体分别进行弹性重力分析和塑性重力分析，生成初始应力场。
b）进行动力分析。首先将重力分析阶段的土体变形重置为0，然后将土体的渗透系数设置为实际值，使用Uniform Excitation命令对模型施加基底一致激励，开始动力分析，在动力分析过程中使用Newmark积分进行求解。考虑到动力分析的稳定性，采用Rayleigh阻尼，主要考虑初始刚度的影响，将初始刚度矩阵系数设为0.002。
1.3 模型可靠性验证
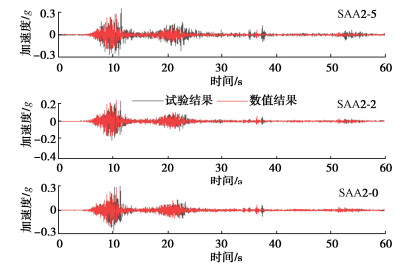
将本文数值模型的计算结果与水平自由场振动台模型试验结果进行对比，来验证数值模型的准确性。图 4为场地土中SAA2-0、SAA2-2、SAA2-5三个测点在0.3g汶川卧龙台地震记录输入下数值模拟结果与试验结果水平方向加速度时程曲线对比。从图 4中可以看出计算值与试验值的加速度峰值较为吻合，峰值出现的时间基本相同，加速度的趋势也基本一致，因此可以得出本文的数值模拟结果能够较为准确地反映不同深度处土体的加速度响应。
![]()
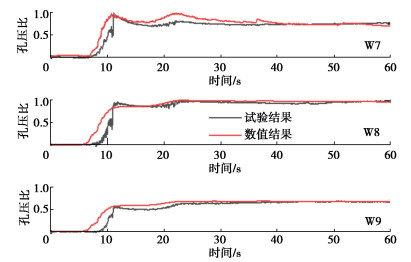
图 4 不同测点处土体加速度时程曲线对比Figure 4. Comparison of time histories of soil acceleration at different test points图 5对比了场地土中W7、W8、W9三个测点处数值模拟结果与试验结果的孔压比时程曲线，由图 5可以看出，本文数值模拟结果与试验结果的孔压比时程响应变化趋势基本一致，孔压比峰值出现的时间也基本相同。但在孔压增长阶段（0~11 s）数值模拟结果的孔压增长先于试验结果，造成这种现象的原因可能是振动台试验中模型箱内壁有一定厚度的橡胶膜以及模型箱层间具有一定的摩擦力，橡胶膜和层间摩擦力的存在会消耗一定的能量，导致数值模拟结果在孔压的上升阶段测点的孔压增长先于试验结果。由图 5同样可以看出，地震动作用的第一阶段以后，数值模拟的孔压比时程曲线结果与试验结果的变化趋势基本一致，但由于橡胶膜和模型箱层间摩擦力的作用，数值模拟的孔压比计算结果仍然略高于试验结果。饱和砂土上部W7处的孔压比时程曲线呈现“双驼峰”型的增长、消散趋势。
![]()
图 5 不同测点处土体孔压比时程曲线对比Figure 5. Comparison of time histories of pore pressure ratio of soil at different test points2. 倾斜自由场动力分析
基于本文提出的数值模拟方法，针对试验中采用的不同倾斜方式以及模型箱类型，分别建立了层剪箱整体倾斜模型（层剪箱与土体整体倾斜2°）、层剪箱场地土倾斜模型（层剪箱保持水平而土体表面倾斜2°）以及刚性箱场地土倾斜模型（刚性箱保持水平土体表面倾斜2°）3种数值模型，选取3个模型中沿水平方向1.6 m中心处不同深度土体的地震动力响应结果进行对比分析，研究不同方式对倾斜液化场地地震动力响应的影响。
2.1 层剪箱整体倾斜模型
在上述水平自由场数值模型的基础上，通过将模型箱底座固定于具有2°坡度的刚性框架表面的方式，将模型箱与场地土整体倾斜2°（简称层剪箱整体倾斜）；并将相同层数模型箱节点的水平方向和竖直方向的自由度绑定以模拟试验中模型箱的实际运动状态，模型的边界条件以及分析步骤与水平自由场模型相同，数值模型如图 6所示。
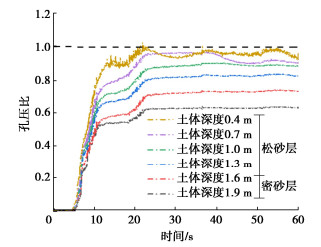
（1）整体倾斜模型土体孔压比响应
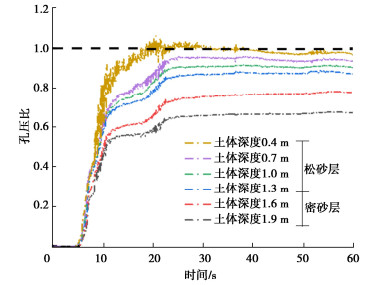
图 7为采用层剪箱整体倾斜模型计算得到的0~60 s时间段内水平方向中心处不同深度土体孔压比的时程曲线。从图 7中可以看出深度越浅的土体孔压比增长速度越快，相同时刻深度越浅的土体孔压比越高；其中深度0.4 m的土体孔压比呈现出“双驼峰”型的增长和消散趋势，相比之下，其他深度处的土体孔压比呈现阶段型增长特性。
![]()
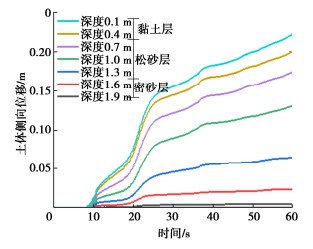
图 7 整体倾斜模型不同深度处土体孔压比时程曲线Figure 7. Time histories of pore pressure ratio of soil at different depths in integral inclined model（2）整体倾斜模型土体侧向位移
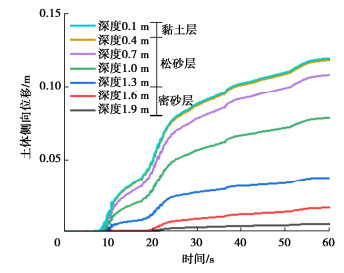
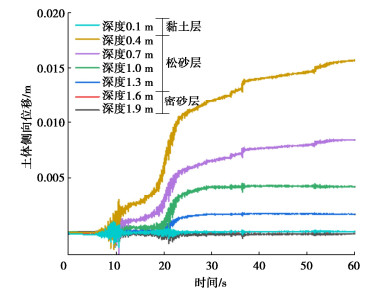
图 8为采用层剪箱整体倾斜模型计算得到不同深度处土体的侧向位移时程曲线。从图 8可以看出，在地震作用下，深度1.9 m处的土体的侧向位移最小，深度0.1 m处土体的侧向位移最大，最大值可达22 cm。
![]()
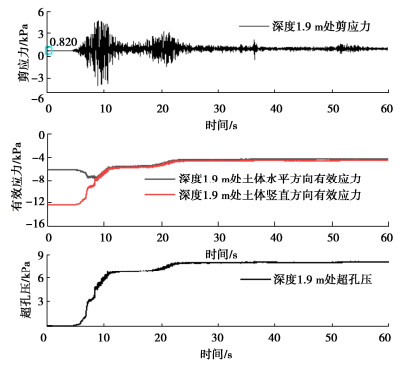
图 8 整体倾斜模型不同深度处土体的侧向位移时程曲线Figure 8. Time histories of lateral displacement of soil at different depths in integral inclined model（3）整体倾斜模型土体剪切应力响应
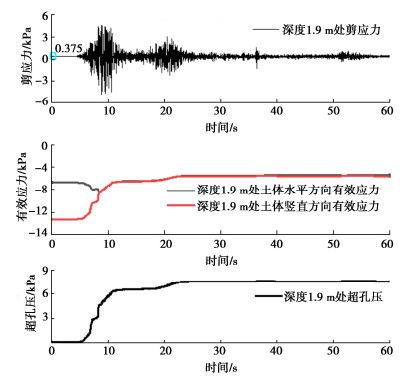
图 9为采用层剪箱整体倾斜模型在地震动作用下，深度1.9 m处土体的超孔压、有效应力以及剪应力的时程变化曲线，其中有效应力为负值表示土体受压。从图 9中可以看出，随着地震动的作用，深度1.9 m处土体的超孔压呈现阶段型增长趋势，水平方向上的有效应力先（负向）增大后（负向）减小，增大的原因可能是土体的剪胀效应；土体竖直方向上的有效应力一直呈现负向减小的趋势，在9 s以后土体水平方向和竖直方向的有效应力曲线基本重合，并在21 s时土体有效应力降到最小值4.5 kPa，21~60 s时间段内土体的有效应力基本保持不变。同时由图可以看出，土体剪应力随时间的变化趋势与加速度的发展趋势相近，由此可以判断出，深度1.9 m处的土体基本未发生剪切破坏。
![]()
图 9 整体倾斜模型深度1.9 m处土体剪切应力时程曲线Figure 9. Time histories of shear stress of soil at depth of 1.9 m in integral inclined model2.2 层剪箱场地土倾斜模型
为了与层剪箱整体倾斜模型动力响应的计算结果进行对比，在水平自由场数值模型的基础上保持模型箱水平，将场地土表面倾斜角度设为2°（简称层剪箱场地土倾斜），建立层剪箱场地土倾斜模型，将土层交界面设置为倾斜2°，土体底部设置为水平，模型的其他边界条件与水平自由场模型相同，模型如图 10所示。
![]()
图 10 层剪箱场地土倾斜有限元计算模型Figure 10. Finite element model for inclined soil at laminar shear box site（1）场地土倾斜模型土体孔压比响应
图 11给出了采用层剪箱场地土倾斜模型计算得到的不同深度处土体孔压比的时程曲线。从图 11中可以看出，与层剪箱整体倾斜模型的结果对比，深度0.4 m处土体的孔压比并没有呈现“双驼峰”型的增长和消散趋势；深度0.7 m处土体的孔压比曲线与层剪箱整体倾斜模型的孔压比曲线趋势基本相同，但37 s后孔压比的减小趋势要小于层剪箱整体倾斜模型；可能的原因是水平模型箱会约束黏土层与饱和砂土层界面处土体的位移，从而使深度较浅处土体的孔压比对加速度的敏感度降低。其他深度处土体的孔压比发展趋势与层剪箱整体倾斜模型的基本相同。
![]()
图 11 场地土倾斜时不同深度处土体孔压比时程曲线Figure 11. Time histories of pore pressure ratio of soil at different depths with inclined soil in shear box（2）场地土倾斜模型土体侧向位移
图 12中给出了采用层剪箱场地土倾斜模型计算得到的不同深度处土体的侧向位移时程曲线，从图 12中可以看出深度1.9 m处土体的侧向位移最小，深度0.1 m处的土体侧向位移最大，最大位移值约为12 cm，深度0.4 m处土体的侧向位移与深度0.1 m处的结果基本相同，可能的原因是水平模型箱约束了黏土层与饱和砂土层界面处土体的侧向位移。深度0.1，0.4，0.7，1.0，1.3 m处土体的侧向位移从5 s开始累积，而深度1.6 m和1.9 m处土体的侧向位移从20 s才开始积累，可能的原因是深度较深的土体在5~20 s时间段内孔压比程度较低，土体未发生剪切破坏。不同深度处土体的侧向位移增长趋势与层剪箱整体倾斜模型情况下的增长趋势基本相同，但数值上要小于层剪箱整体倾斜模型的计算结果。
![]()
图 12 场地土倾斜时不同深度处土体侧向位移时程曲线Figure 12. Time histories of lateral displacement of soil at different depths with inclined soil in shear box（3）场地土倾斜模型土体剪切应力响应
图 13给出了采用层剪箱场地土倾斜模型计算得到的深度1.9 m处土体超孔压、有效应力、剪应力时程曲线，与图 9对比可以看出层剪箱场地土倾斜模型深度1.9 m处土体的初始剪应力（图 13中的0.375 kPa）小于层剪箱整体倾斜模型（图 9中的0.820 kPa）的初始剪应力，可能的原因是层剪箱整体倾斜模型中滑动面上部土体的重力沿滑动方向分力较大，而在层剪箱场地土倾斜模型中滑动面上部土体的重力沿滑动方向分力较小导致的。
![]()
图 13 场地土倾斜时深度1.9 m处土体剪切应力时程曲线Figure 13. Time histories of shear stress of soil at depth of 1.9 m with inclined soil in shear box2.3 刚性箱场地土倾斜模型
在振动台模型试验中，为了模拟土体在地震动作用下的动力响应，通常采用层剪箱作为模型箱，层剪箱可以有效地模拟土体在地震作用下的动力反应。但是受试验条件的限制，有些情况下也会采用尺寸较大的刚性箱进行地震反应振动台模型试验。本文在层剪箱场地土倾斜模型的基础上，将模型箱单元之间的零长单元连接换成刚性连接，将模型箱与土体相邻处节点水平和竖直方向的自由度进行绑定，模型的其他边界条件以及分析步骤保持不变，建立了刚性箱场地土倾斜模型（刚性箱保持水平土体表面倾斜2°），以此来模拟采用刚性箱进行地震反应振动台模型试验的情况，所建立的模型如图 14所示。
![]()
图 14 刚性箱场地土倾斜有限元计算模型Figure 14. Finite element calculation model of inclined soil in rigid box（1）刚性箱模型土体孔压比响应
图 15为采用刚性箱场地土倾斜模型计算得到的不同深度处土体的孔压比时程曲线。从图 15中可以看出，深度0.4，0.7，1.0 m处土体的孔压比呈现阶段型增长趋势。深度1.3，1.6，1.9 m处土体的孔压比呈现出“双驼峰”型的增长和消散趋势。相比之下，刚性箱场地土倾斜模型土体的孔压比比层剪箱整体倾斜模型和层剪箱场地土倾斜模型小。
![]()
图 15 刚性箱模型不同深度处土体孔压比时程曲线Figure 15. Time histories of pore pressure ratio of soil at different depths in rigid box（2）刚性箱模型土体侧向位移
图 16为采用刚性箱场地土倾斜模型计算得到的不同深度处土体的侧向位移时程曲线。从图 16中可以看出深度0.4 m处土体的侧向位移最大，最大值为1.5 cm。深度0.7，1.0，1.3 m处土体随着深度的增加土体侧向位移逐渐减小。深度1.6，1.9 m的土体侧向位移值很小，并且土体侧向位移的发展趋势与加速度的趋势相近。深度0.1 m处的土体侧向位移值也很小，可能的原因是刚性箱限制了黏土层与饱和砂土层界面处土体的侧向位移，且黏土层由于黏聚力的原因在地震动作用下土体的侧向位移较小。
![]()
图 16 刚性箱模型时不同深度处土体侧向位移时程曲线Figure 16. Time histories of lateral displacement of soil at different depths in rigid box3. 不同倾斜方式对场地响应的影响
上述分析分别针对层剪箱整体倾斜、层剪箱场地土倾斜、刚性箱场地土倾斜3种不同倾斜方式下倾斜液化场地土在地震作用下的动力响应进行了计算和讨论。为了更清晰地比较3种不同方式下倾斜自由场场地土地震动力响应和液化特性，将3种不同倾斜方式下场地土的孔压比、侧向位移以及加速度等计算结果进行对比分析，以此分析不同倾斜方式对倾斜液化场地地震动力特性的影响。
3.1 土体孔压比结果对比
由上述图 7与图 11的计算结果可以看出，采用层剪箱整体倾斜与层剪箱场地土倾斜两种倾斜方式时，相同深度处场地土的孔压比变化趋势和大小基本相同。而由图 15与图 7和图 11对比可以看出，采用刚性箱场地土倾斜试验方法时相同深度处场地土的孔压比会比采用层剪箱整体倾斜与层剪箱场地土倾斜两种试验方法的结果小。对比3种模拟方法，可以发现采用刚性箱的试验方法会导致土体孔压比响应偏小，而采用层剪箱整体倾斜与层剪箱场地土倾斜两种方式对场地土体的孔压比响应计算结果影响较小。
3.2 土体的侧向位移结果对比
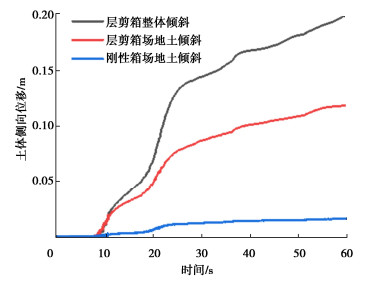
图 17给出了3种不同倾斜方式深度0.4 m处土体的侧向位移时程结果对比。从图 17中可以看出，相同的地震动作用和相同的土层条件下，采用3种不同倾斜方式计算得到的深度0.4 m处土体的侧向位移结果分别为20，12，1.5 cm。通过对3个模型的计算结果进行比较可以发现，不同的模型箱对土体的侧向位移有很大的影响，刚性箱在很大程度上限制了土体侧向位移的发展。另外，通过分析层剪箱整体倾斜和场地土倾斜两种模型的计算结果可以发现，在地震动作用8~11 s时间段内采用两个模型计算得到的土体侧向位移结果基本相同，但在地震动作用11~60 s时间段内采用层剪箱整体倾斜模型计算得到的土体侧向位移的累积明显高于采用层剪箱场地土倾斜模型。
![]()
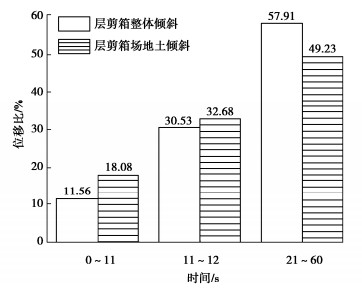
图 17 3种不同方式下土体侧向位移时程对比Figure 17. Comparison of time histories of lateral displacement of soil with three different modes图 18给出了采用层剪箱整体倾斜模型与层剪箱场地土倾斜模型计算得到的在地震动作用时间段内，最大的土体侧向位移与最终时刻最大土体侧向位移占比图。结合图 17可知，采用层剪箱场地土倾斜的方式会约束土体的侧向位移，且在地震作用后期（21~60 s）对土体的侧向位移的约束更为明显。
![]()
图 18 层剪箱模型不同阶段土体侧向位移占比对比Figure 18. Comparison of proportions of lateral displacement of soil at different stages in laminar shear box3.3 土体加速度结果对比
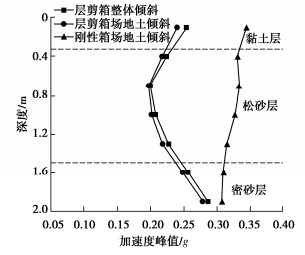
图 19给出了采用3个不同数值模型计算得到的加速度峰值反应沿土层深度的分布。从图 19中可以看出，采用刚性箱场地土倾斜模型计算的场地土加速度峰值大于输入地震动加速度的峰值，并沿着土层向上呈现增加的趋势；采用层剪箱的两个模型计算得到的场地土加速度峰值在土层深度上的变化趋势基本相同，都呈现“K”形分布。
![]()
图 19 不同深度处土体加速度峰值对比Figure 19. Comparison of acceleration peaks of soil at different depths4. 结语
本文首先根据水平自由场振动台模型试验建立了水平自由场数值模型，考虑了模型箱对场地土地震响应的影响；在此基础上分别建立了层剪箱整体倾斜模型、层剪箱场地土倾斜模型以及刚性箱场地土倾斜模型模拟3种不同的倾斜方式；最后对3个数值模型计算得到的自由场场地土地震动力响应结果进行对比分析。得到了以下认识：在模拟倾斜液化场地地震动力响应的数值模型中，采用层状剪切模型箱时，模型箱整体倾斜与场地土倾斜两种倾斜方式在土体侧向位移响应上差别较大，而采用刚性箱场地土倾斜的试验方法与层剪箱的试验方法在土体孔隙水压力、土体侧向位移以及加速度响应上均有更为明显的差别。通过振动台试验研究倾斜液化场地的侧扩流问题时，使用模型箱整体倾斜的试验方法对土体的侧向位移约束最小。
-
![]()
图 1 水平自由场振动台模型试验传感器布置图
Figure 1. Layout of sensors for shaking table tests on horizontal free field
![]()
图 2 汶川地震卧龙台地震记录加速度时程曲线
Figure 2. Time histories of acceleration recorded at Wolong station of Wenchuan earthquake
![]()
图 4 不同测点处土体加速度时程曲线对比
Figure 4. Comparison of time histories of soil acceleration at different test points
![]()
图 5 不同测点处土体孔压比时程曲线对比
Figure 5. Comparison of time histories of pore pressure ratio of soil at different test points
![]()
图 7 整体倾斜模型不同深度处土体孔压比时程曲线
Figure 7. Time histories of pore pressure ratio of soil at different depths in integral inclined model
![]()
图 8 整体倾斜模型不同深度处土体的侧向位移时程曲线
Figure 8. Time histories of lateral displacement of soil at different depths in integral inclined model
![]()
图 9 整体倾斜模型深度1.9 m处土体剪切应力时程曲线
Figure 9. Time histories of shear stress of soil at depth of 1.9 m in integral inclined model
![]()
图 10 层剪箱场地土倾斜有限元计算模型
Figure 10. Finite element model for inclined soil at laminar shear box site
![]()
图 11 场地土倾斜时不同深度处土体孔压比时程曲线
Figure 11. Time histories of pore pressure ratio of soil at different depths with inclined soil in shear box
![]()
图 12 场地土倾斜时不同深度处土体侧向位移时程曲线
Figure 12. Time histories of lateral displacement of soil at different depths with inclined soil in shear box
![]()
图 13 场地土倾斜时深度1.9 m处土体剪切应力时程曲线
Figure 13. Time histories of shear stress of soil at depth of 1.9 m with inclined soil in shear box
![]()
图 14 刚性箱场地土倾斜有限元计算模型
Figure 14. Finite element calculation model of inclined soil in rigid box
![]()
图 15 刚性箱模型不同深度处土体孔压比时程曲线
Figure 15. Time histories of pore pressure ratio of soil at different depths in rigid box
![]()
图 16 刚性箱模型时不同深度处土体侧向位移时程曲线
Figure 16. Time histories of lateral displacement of soil at different depths in rigid box
![]()
图 17 3种不同方式下土体侧向位移时程对比
Figure 17. Comparison of time histories of lateral displacement of soil with three different modes
![]()
图 18 层剪箱模型不同阶段土体侧向位移占比对比
Figure 18. Comparison of proportions of lateral displacement of soil at different stages in laminar shear box
![]()
图 19 不同深度处土体加速度峰值对比
Figure 19. Comparison of acceleration peaks of soil at different depths
表 1 饱和砂土模型参数
Table 1 Parameters of saturated sand model
参数 密砂层 饱和松砂层 密度ρ/(kg·m-3) 1900 1700 参考剪切模量Gr/kPa 70000 60000 参考体积模量Br/kPa 190000 160000 摩擦角ϕ 33.5 31 峰值剪应变γmax 0.1 0.1 参考围压p/kPa 101 101 压力系数n 0.5 0.5 剪胀角ϕPT 25.5 31 剪缩参数c1 0.045 0.087 剪缩参数c3 0.15 0.21 剪胀参数d1 0.06 0 剪胀参数d3 0.15 0 屈服面数 20 20 初始孔隙比e 0.7 0.85 标准大气压常量/kPa 101 101 
下载: 导出CSV
表 2 上覆黏土模型参数
Table 2 Parameters of overlaid clay model
参数 黏土层 质量密度ρ/(kg·m-3) 1300 参考剪切模量Gr/kPa 13000 参考体积模量Br/kPa 65000 黏聚力c/kPa 18 峰值剪应变γmax 0.1 参考围压p/kPa 100 压力系数n 0 屈服面数 20 摩擦角ϕ 0
下载: 导出CSV
-
[1] 许成顺, 贾科敏, 杜修力, 等. 液化侧向扩展场地-桩基础抗震研究综述[J]. 防灾减灾工程学报, 2021, 41(4): 768-791. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202104009.htm XU Chengshun, JIA Kemin, DU Xiuli, et al. Review on seismic behavior of pile foundation subjected to liquefaction induced lateral spreading[J]. Journal of Disaster Prevention and Mitigation Engineering, 2021, 41(4): 768-791. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK202104009.htm
[2] HAMADA M, YASUDA S, ISOYAMA R, et al. Study on liquefaction induced permanent ground displacements and earthquake damage[J]. Proceedings of Japan Society of Civil Engineers, 1986(376): 221-229.
[3] ZHOU Y G, XIA P, LING D S, et al. A liquefaction case study of gently sloping gravelly soil deposits in the nearfault region of the 2008 Mw 7.9 Wenchuan Earthquake[J]. Bulletin of Earthquake Engineering, 2020, 18(14): 6181-6201. doi: 10.1007/s10518-020-00939-4
[4] BRUNET S, DE LA LLERA J C, JACOBSEN A, et al. Performance of port facilities in southern Chile during the 27 February 2010 Maule Earthquake[J]. Earthquake Spectra, 2012, 28(S1): 553-579.
[5] BRADLEY K, MALLICK R, ANDIKAGUMI H, et al. Earthquake-triggered 2018 Palu Valley Landslides Enabled by Wet Rice Cultivation[J]. Nature Geoscience, 2019, 12(11): 935-939. doi: 10.1038/s41561-019-0444-1
[6] DOBRY R, THEVANAYAGAM S, MEDINA C, et al. Mechanics of lateral spreading observed in a full-scale shake test[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(2): 115-129. doi: 10.1061/(ASCE)GT.1943-5606.0000409
[7] CHANG B J, HUTCHINSON T C. Experimental investigation of plastic demands in piles embedded in multi-layered liquefiable soils[J]. Soil Dynamic and Earthquake Engineering, 2013, 49(3): 146-156.
[8] JIA K M, XU C S, EL NAGGAR M H, et al. Large-scale shake table testing of pile group-bridge model in inclined liquefiable soils with overlying crusts[J]. Soil Dynamics and Earthquake Engineering, 2022, 163: 107555. doi: 10.1016/j.soildyn.2022.107555
[9] 张鑫磊, 王志华, 许振巍, 等. 土体液化大位移条件下群桩动力反应振动台模型试验[J]. 工程力学, 2016, 33(5): 150-156. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201605019.htm ZHANG Xinlei, WANG Zhihua, XU Zhenwei, et al. Shaking table model tests on dynamic response of pile groups under liquefaction-induced large ground displacement[J]. Engineering Mechanics, 2016, 33(5): 150-156. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201605019.htm
[10] ELGAMAL A, YANG Z, PARRA E. Computational modeling of cyclic mobility and post-liquefaction site response[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(4): 259-271. doi: 10.1016/S0267-7261(02)00022-2
[11] 周林禄, 苏雷, 邱志坚, 等. 基于OpenSees的砂土本构模型对比研究[J]. 地震工程学报, 2022, 44(1): 128-135, 151. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ202201016.htm ZHOU Linlu, SU Lei, QIU Zhijian, et al. Comparison of four constitutive models for sand based on OpenSees[J]. China Earthquake Engineering Journal, 2022, 44(1): 128-135, 151. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ202201016.htm
[12] SU L, WAN H P, LUO Y Z, et al. Seismic performance assessment of a pile-supported wharf retrofitted with different slope strengthening strategies[J]. Soil Dynamics and Earthquake Engineering, 2020, 129: 105903. doi: 10.1016/j.soildyn.2019.105903
[13] MAZZONI S, MCKENNA F, SCOTT M H, et al. OpenSees Command Language Manual[R]. Berkeley: Pacific Earthquake Engineering Research Center, 2006.
[14] 许成顺, 豆鹏飞, 杜修力, 等. 液化自由场地震响应大型振动台模型试验分析[J]. 岩土力学, 2019, 40(10): 3767-3777. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201910010.htm XU Chengshun, DOU Pengfei, DU Xiuli, et al. Large-scale shaking table model test of liquefiable free field[J]. Rock and Soil Mechanics, 2019, 40(10): 3767-3777. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201910010.htm
-
其他相关附件
计量
- 文章访问数: 347
- HTML全文浏览量: 52
- PDF下载量: 95
