装配式框架预应力锚索支护结构承载特性及装配式框架计算方法研究

郭楠; 陆发; 杨校辉; 马天忠

doi:10.11779/CJGE2022S1045

装配式框架预应力锚索支护结构承载特性及装配式框架计算方法研究 English Version

郭楠^{1, 2,},
陆发^{1, 2},
杨校辉^{1, 2, ,},
马天忠^{1, 2}

1.
兰州理工大学土木工程学院, 甘肃兰州 730050
2.
兰州理工大学西部土木工程防灾减灾教育部工程研究中心, 甘肃兰州 730050

基金项目:

甘肃省科技计划项目 20JR10RA200

甘肃省科技计划项目 20JR5RA434

甘肃省住房和城乡建设厅建设科技项目 JK2021-46

甘肃省住房和城乡建设厅建设科技项目 JK2021-55

国家自然科学基金项目 52168051

国家自然科学基金项目 52068048

详细信息

作者简介:
郭楠(1987—)，女，博士，副教授，主要从事非饱和土与特殊土力学、支挡结构等方面的研究工作。E-mail: 355094754@qq.com

通讯作者:
杨校辉，E-mail: yxhui86@126.com

中图分类号: TU449
计量
- 文章访问数: 138
- HTML全文浏览量: 42
- PDF下载量: 24
出版历程
- 收稿日期: 2022-09-24
- 网络出版日期: 2023-02-06
- 刊出日期: 2022-11-30

Bearing characteristics and method of prefabricated for support structure frame-prestressed anchor cable

GUO Nan^{1, 2,},
LU Fa^{1, 2},
YANG Xiao-hui^{1, 2, ,},
MA Tian-zhong^{1, 2}

1.
School of Civil Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
Western Engineering Research Center of Disaster Mitigation in Civil Engineering of Ministry of Education, Lanzhou University of Technology, Lanzhou 730050, China

摘要

摘要: 框架预应力锚索支护结构用于快速应急滑坡加固或边坡支护工程尚具有局限性，同时现有的变截面装配式框架预应力锚索支护结构的节点易破坏或易发生不均匀沉降。对此，提出了一种新型等截面装配式框架预应力锚索支护结构，通过数值模拟、现场监测试验、理论推导等手段，深入研究了该结构的承载特性、设计方法。结果表明：新型装配式框架结构主要由等截面的预制构件和节点组成，具有施工方便、效率高等优点；该结构立柱应力较大、横梁应力较小，两者的应变均随着高度增加而变大，但是该结构节点强度较低，特别是立柱上的节点；随着该结构上施加的附加荷载增大，框架底部应力增大、顶部应力减小，框架整体应变线性增大；根据装配式框架结构的承载特性和节点变形情况，给出三种装配式框架结构设计计算方法，可运用于实际工程设计。以上研究可为装配式框架预应力锚索支护结构设计施工提供科学依据。
- 装配式框架预应力锚索 /
- 支护结构 /
- 承载特性 /
- 数值模拟 /
- 现场监测
Abstract: The support structure of frame-prestressed anchor cable has limitations in the rapid emergency landslide reinforcement or slope support projects. At the same time, the existing support structure of variable cross-section prefabricated frame-prestressed anchor cable is prone to damage or uneven settlement. A new type of pre-stressed anchor cable support structure with equal cross-section fabricated frame is proposed. Through the numerical simulations, field monitoring tests and theoretical researches, the bearing characteristics and design methods of the structure are deeply studied. The results show that the new fabricated frame structure is mainly composed of prefabricated members and joints with equal section, and it has the advantages of convenient construction and high efficiency. The column stress of the structure is large and the beam stress is small. The strains of both of them increase with the increase of the height, but the strength of the structural node is low, especially the node on the column. With the increase of the additional loads on the structure, the bottom stress of the frame increases, the top stress decreases, and the overall strain of the frame increases linearly. According to the load-bearing characteristics and node deformation of the prefabricated frame structure, three design methods for the prefabricated frame structure are put forward, which can be applied to practical engineering design. The above researches may provide scientific basis for the design and construction of support structure of prefabricated frame-prestressed anchor cable.
- prefabricated frame-prestressed anchor cable /
- support structure /
- bearing characteristic /
- numerical simulation /
- field monitoring

HTML全文

0. 引言

近年来，西北地区边（滑）坡支护工程日益增多。框架预应力锚索支护结构^[1]以其传力路径明确、稳定性好、造价低等优点，广泛应用于边坡、滑坡支护工程；但是该支护结构的框架梁施工工序繁琐、养护周期长、机械化程度低，特别是对于快速应急高陡边坡支护或滑坡加固^[2]局限性明显。

鉴于建筑工程中装配式结构具有施工快、保护环境、可拆卸、易安装等优点^[3]，苏俊霞等^[4]提出采用两根单向变截面梁拼装成十字架的拼装式锚杆（索）框架结构，应当指出，该框架结构破坏出现在框架的节点处、易产生不均匀变形；郑静等^[5]进一步提出双向变截面梁的拼装式锚杆框架结构并进行了该结构的现场试验研究。杨校辉等^[6-7]改进提出了新型装配式框架预应力锚索支护结构及节点连接部件。因此，装配式框架预应力锚索支护结构亟待开展深入研究。

有关装配式框架预应力锚索支护结构承载特性方面，苏俊霞等^[4]采用数值模拟和现场试验进行了单向变截面梁拼装式锚杆框架结构的力学特征研究，郑静等^[5]采用现场试验进行了双向变截面梁拼装式锚杆框架结构的受力和变形特征研究，发现拼装构件凹槽空隙部分处理不当时会造成节点顶部有明显的应力集中现象和挤裂变形。上述有关变截面承载特性研究发现，此类变截面装配式框架结构节点具有易变形和明显应力集中的不足；相关研究均未采用数值模拟软件对附加荷载作用下结构承载特性做进一步探索。因此，有必要进一步开展等截面装配式框架梁承载特性的研究。

有关装配式框架预应力锚索支护结构的计算目前鲜见文献报道，文献[8]是按照规范采用现浇框架预应力锚索支护结构算法进行设计。其中现浇框架预应力锚索支护结构一般采用计算模型有倒梁法、文克勒地基梁、弹性半空间体、双参数模型等^[9-10]。由于弹性半空间体、双参数模型设计计算过程复杂，倒梁法没有考虑框架和土体相互作用，故采用文克勒地基梁模型进行结构设计较适宜。当装配式框架节点变形情况不同时，其可简化为不同支座的单跨梁，但是装配式框架结构和现浇框架结构的简化模型及边界条件不同，因此基于文克勒地基梁模型提出装配式框预应力锚索支护结构内力设计计算方法。

综上所述，针对快速应急高陡边坡支护或滑坡加固需求，本文提出了一种新型装配式框架支护结构，采用数值模拟揭示其承载特性，同时，基于装配式框架节点变形情况，建立了装配式框架结构设计内力计算方法。研究成果可为装配式框架预应力锚索支护结构设计提供参考。

1. 装配式框架预应力锚索支护结构

1.1 装配式框架支护结构组成

现有装配式框架锚索支护结构可分为拼装式、卯榫搭接型、钢节点连接型、十字格构型等，但是这些装配式框架构件多为变截面梁，具有破坏出现在框架的节点处、易于产生不均匀变形、耐久性低等不足^[4-8]。基于此，提出一种具有等截面的新型装配式框架预应力锚索支护结构。

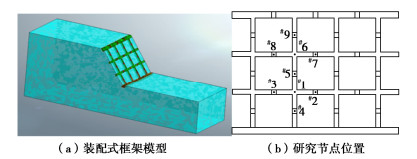
该新型支护结构以现浇框架横梁、立柱的结构为基础，将现浇框架划分成预制构件、节点，如图 1（a）。预制构件为钢筋混凝土构件，按形状不同构件可分为“十字型”构件A、“T型”构件B和“L型”构件C，预制构件梁为矩形截面，且中部设有预留的锚索孔，如图 1（b）~（d）型钢接头的预制构件所示。节点先采用钢筋焊接或型钢螺栓连接等方式连接，再浇筑混凝土；当节点为型钢螺栓连接时，如下图 1（e），预制构件各端部设有H型钢接头和4个螺栓孔。

图 1 装配式框架预应力锚索支护结构

Figure 1. Support structure of prefabricated frame-prestressed anchor.cable

下载: 全尺寸图片幻灯片

1.2 装配式框架预应力锚索支护结构施工

装配式框架预应力锚索支护结构施工步骤主要有预制构件（施工准备和入模、振捣、养护）、边坡修整、成孔、构件安装、锚索施工、构件的连接等，施工流程见图 2。其中锚索施工与现浇框架预应力锚索施工相同。由图 2可知，该支护结构的框架梁可以在边坡修整和锚索成孔的同时进行预制，有效缩短工期，预制过程中机械化程度提高、劳动力可降至最低，特别适合一些情况较为危急的边坡或滑坡治理工程。

图 2 装配式框架施工流程

Figure 2. Construction process of fabricated frame

下载: 全尺寸图片幻灯片

2. 承载特性研究

为了研究装配式框架预应力锚索支护结构承载特性，采用MIDAS GTS有限元软件分别对在不同压力下作用下装配式框架预应力锚索支护结构的应力、应变规律进行分析。

2.1 数值模型

某均质边坡坡体高为8 m，坡率为1∶0.75，分别采用装配式框架预应力锚索和现浇框架预应力锚索支护。框架梁断面尺寸均为0.3 m×0.35 m，锚索水平间距均为2.8 m，竖向间距均为2.6 m，锚索倾角均为15°，锚索自由段5 m，锚固段6 m，装配式框架节点尺寸为0.3 m×0.3 m×0.35 m。数值模拟相关参数见表 1，其中黄土参数由地勘报告确定。

表 1 数值模拟所用材料相关参数

Table 1. Material parameters used in numerical simulation

名称	重度/(kN·m^-3)	泊松比	弹性模量/MPa	内摩擦角/(°)	黏聚力/kPa	本构模型	属性
黄土	16.4	0.30	18.5	19	22	莫尔库仑	3D实体
装配式构件	26.0	0.20	2.8×10⁴	—	—	弹性	3D实体
节点	21.0	0.31	3.0×10⁴	—	—	弹性	3D实体
锚索	77.0	0.22	1.05×10⁵	—	—	弹性	1D植入式桁架

下载: 导出CSV

| 显示表格

装配式框架和现浇框架三维模型如图 3所示。由于作用荷载、框架结构对称，故研究左面靠近中心影响较大的两个构件，分别取图 3各点研究。

图 3 三维模型

Figure 3. Three-dimensional model

下载: 全尺寸图片幻灯片

2.2 有限元结果分析

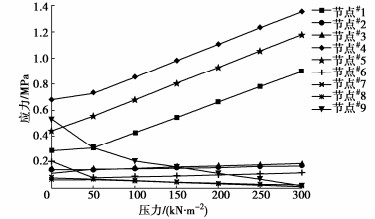
图 4，5分别为装配式框架施加不同压力的应力和应变变化规律图。

图 4 装配式框架各节点应力变化规律图

Figure 4. Variation of stress of each node of prefabricated frame

下载: 全尺寸图片幻灯片

图 5 装配式框架各节点应变变化规律图

Figure 5. Variation of strain of each node of prefabricated frame

下载: 全尺寸图片幻灯片

由图 4可知，节点^#1，^#4，^#5的应力随着压力增大而增大，节点^#7，^#8，^#9应力变化相反，其余节点应力皆近似保持不变。由图 5可知，随着压力的增大装配式框架^#5~^#9节点变形近似线性增大，^#1~^#4节点应力在压力为50 kN/m²时发生突变，而且靠近坡顶节点应变越小、靠近坡底应变越大；预制构件连接处节点处的应变最大，尤其施加压力为300 kN/m²时^#4，^#5节点应变已经达到2844 με，此时^#1节点变形仅为1532 με。因为该结构不施加压力时重力要大于土压力，故随着其施加的压力增大^#1~^#4节点应力先减小、后增大。根据以上模拟可知：预制构件连接处节点强度较低；装配式框架底部应力随着压力的增大而增大，顶部应力变化相反；装配式框架应变随着压力的增大呈线性增大；附加压力不大于300 kN/m²时，装配式框架结构承载能力较好。

3. 装配式框架结构设计内力计算方法

根据装配式框架结构承载特性，首先将装配式框架简化为预制构件的梁进行设计；其次通过节点荷载分配系数，将锚索拉力分配到每个预制构件梁上；再次考虑结构和土体的变形协调条件，提出3种不同支座构件内力算法，进行框架结构设计内力计算；最后依据规范进行预制构件配筋设计。

3.1 分配节点荷载

装配式框架预制构件中心荷载为锚索拉力，锚索拉力根据传统现浇锚索计算公式求解。预制构件中心荷载进行分配计算时，不需要考虑节点处可能存在的微小转角及相邻荷载的影响，但是要满足静力平衡和变形协调条件^[11-12]。因此，假定装配式框架梁为铰接，忽略转角与扭矩，得到预制构件中心荷载分配公式：

$\begin{gathered} {k_i} = \frac{{{p_i}}}{p} \hfill \\ \begin{array}{*{20}{c}} {} \\ {} \end{array} = \frac{{{{({\lambda ^i})}^3}E{I^i}}}{{PF_4^i(x - {x_p})}} \hfill \\ \left[\left(({w}_{0}{F}_{1}^{i}(x))+\frac{{\theta }_{0}^{i}}{{\lambda }^{i}}{F}_{2}^{i}(x)-\frac{{M}_{0}^{i}}{{({\lambda }^{i})}^{2}E{I}^{i}}{F}_{3}^{i}(x)-\frac{{Q}_{i}^{0}}{{({\lambda }^{i})}^{3}E{I}^{i}}{F}_{4}^{i}(x)\right)-{w}_{i}\right]。 \end{gathered}$

(1)

式中w为梁的挠度；θ为角度；M为弯矩；Q为剪力；E为梁材料的弹性模量；I为梁的截面惯性矩；k为基床系数；b为梁的宽度； $\lambda$ 为梁的柔度特征值， $\lambda = \sqrt[4]{{\frac{{kb}}{{4EI}}}}$ ；P为节点处受集中荷载（kN）； ${P_i}$ 为每个单梁分配荷载（kN）； ${y_i}$ 为每个单梁的方向位移（m）；F₁(x)、F₂(x)、F₃(x)、F₄(x)为文克勒弹性地基模型参数。

当预制构件每个梁长度近似相等，将锚索拉力平均分配预制构件的每个梁。此时，十字型分配系数取1/4，T型分配系数取1/3、L型分配系数取1/2。

3.2 不同支座构件内力算法

根据装配式框架支护边（滑）坡设计的安全等级和工程实践发现，同边坡上节点变形控制不同，不同边坡的节点变形控制也不同。故考虑结构受力和节点变形，给出左侧为滑动支座和右侧为铰支座、弹簧支座、固定端3种模型的算法。当节点处为铰支座、弹簧支座时允许转动，当节点处为固定端时不容许变形。

（1）铰支座算法

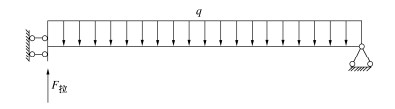
a）简化模型1

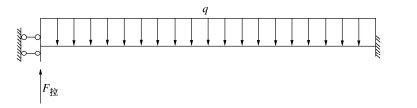
结构简化模型靠近构件中心为滑动支座、节点连接处为铰支座，此时节点处容许变形，如图 6。

图 6 框架简化模型1

Figure 6. Simplified frame model 1

下载: 全尺寸图片幻灯片

b）内力计算公式

根据边界条件，求解得

${M_0} = P \cdot \frac{{{\lambda ^4}EI{F_1}(x){F_2}(x) + kb{F_3}(x){F_4}(x)}}{{{\lambda ^5}EI{F_1}^2(x) + \lambda kb{F_3}^2(x)}}\text{，}$

(2)

${w}_{0}=\frac{P\lambda }{kb{F}_{3}(x)}\cdot \left[{F}_{2}(x)-{F}_{1}(x)\frac{{\lambda }^{4}EI{F}_{1}(x){F}_{2}(x)+kb{F}_{3}(x){F}_{4}(x)}{{\lambda }^{4}EI{F}_{1}{}^{2}(x)+kb{F}_{3}{}^{2}(x)}\right]\text{，}$

(3)

$\theta (x) = - 4\lambda {w_0}{F_4}(x) - \frac{{{M_0}}}{{\lambda EI}}{F_2}(x) - \frac{P}{{{\lambda ^2}EI}}{F_3}(x)\text{，}$

(4)

$Q(x) = \frac{{kb{w_0}}}{\lambda }{F_2}(x) - 4\lambda {M_0}{F_4}(x) - \frac{P}{\lambda }{F_2}(x)。$

(5)

（2）弹簧支座算法

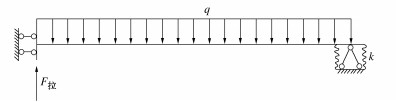
a）简化模型2

将结构简化为靠近构件中心为滑动支座、节点连接处为弹性支座，此时节点处容许变形，框架简化模型如图 7。

图 7 框架简化模型2

Figure 7. Simplified frame model 2

下载: 全尺寸图片幻灯片

b）内力计算公式

根据位移法和边界条件，得

${M_0} = \frac{P}{\lambda } \cdot \frac{{4F_4^2(x) + {F_1}(x){F_3}(x)}}{{4{F_3}(x){F_4}(x) + {F_1}(x){F_2}(x)}}\text{，}$

(6)

${w}_{0}=\frac{P}{{\lambda }^{3}EI{F}_{1}(x)}\cdot \left[{F}_{1}(x)\cdot \frac{4{F}_{4}{}^{2}(x)+{F}_{1}(x){F}_{3}(x)}{4{F}_{3}(x){F}_{4}(x)+{F}_{1}(x){F}_{2}(x)}-{F}_{4}(x)\right]\text{，}$

(7)

$M(x) = \frac{{kb{w_0}}}{{{\lambda ^2}}}{F_3}(x){\text{ + }}{M_0}{F_1}(x) - \frac{P}{\lambda }{F_2}(x)\text{，}$

(8)

$Q(x) = \frac{{kb{w_0}}}{\lambda }{F_2}(x) - 4\lambda {M_0}{F_4}(x) - \frac{P}{\lambda }{F_2}(x)\text{，}$

(9)

${\Delta _1} = \frac{{ - {F_{1p}}}}{{{k_{11}}}} = \frac{{ - M(l)}}{{EI + k}}\text{，}$

(10)

${M}_{总}\text{(}x\text{)}=\frac{-M(l)}{EI+k}\cdot EI\text{+}\frac{kb{w}_{0}}{{\lambda }^{2}}{F}_{3}(x)\text{+}{M}_{0}{F}_{1}(x)-\frac{P}{\lambda }{F}_{2}(x)\text{ }。$

(11)

（3）固定支座算法

由于该结构节点处限制变形，而预制构件中心处存在弯矩，故将结构简化为靠近构件中心为滑动支座、节点连接处为固定端。框架简化模型如图 8。

图 8 框架简化模型3

Figure 8. Simplified frame model 3

下载: 全尺寸图片幻灯片

弹簧支座算法简化模型施加约束时，基本体系为左侧滑动支座、右侧固定端。故边界条件与弹簧支座算法进行位移法推导时模型边界条件相同，内力计算公式为式（6）~（9）。

4. 结论

（1）本文提出了一种由预制构件、节点组成的新型等截面装配式框架预应力锚索支护结构。该结构具有施工方便、工期短、耐久性好、不易变形等优点。通过数值模拟结果发现，该新型结构承载能力较好，可用于应急救灾的边坡和滑坡工程。

（2）装配式框架预应力锚索支护结构的立柱应力较大、横梁应力较小，两者的应变均随着高度增加而变大，预制构件连接处节点强度较低。随着装配式框架结构上施加的附加荷载增大，框架底部应力增大、顶部应力减小，框架整体应变线性增大。

（3）本文提出的3种装配式框架结构设计计算公式，可以反映节点不同变形情况下预制构件弯矩的变化。其中铰支座计算方法更加安全，可用于装配式框架预应力锚索支护结构设计。

图 1 装配式框架预应力锚索支护结构

Figure 1. Support structure of prefabricated frame-prestressed anchor.cable

下载: 全尺寸图片幻灯片

图 2 装配式框架施工流程

Figure 2. Construction process of fabricated frame

下载: 全尺寸图片幻灯片

图 3 三维模型

Figure 3. Three-dimensional model

下载: 全尺寸图片幻灯片

图 4 装配式框架各节点应力变化规律图

Figure 4. Variation of stress of each node of prefabricated frame

下载: 全尺寸图片幻灯片

图 5 装配式框架各节点应变变化规律图

Figure 5. Variation of strain of each node of prefabricated frame

下载: 全尺寸图片幻灯片

图 6 框架简化模型1

Figure 6. Simplified frame model 1

下载: 全尺寸图片幻灯片

图 7 框架简化模型2

Figure 7. Simplified frame model 2

下载: 全尺寸图片幻灯片

图 8 框架简化模型3

Figure 8. Simplified frame model 3

下载: 全尺寸图片幻灯片

表 1 数值模拟所用材料相关参数

Table 1 Material parameters used in numerical simulation

名称	重度/(kN·m^-3)	泊松比	弹性模量/MPa	内摩擦角/(°)	黏聚力/kPa	本构模型	属性
黄土	16.4	0.30	18.5	19	22	莫尔库仑	3D实体
装配式构件	26.0	0.20	2.8×10⁴	—	—	弹性	3D实体
节点	21.0	0.31	3.0×10⁴	—	—	弹性	3D实体
锚索	77.0	0.22	1.05×10⁵	—	—	弹性	1D植入式桁架

下载: 导出CSV

参考文献(12)

[1]	朱彦鹏, 侯喜楠, 马响响, 等. 框架预应力锚杆支护边坡稳定性极限分析[J]. 岩土工程学报, 2021, 43(增刊1): 7–12. doi: 10.11779/CJGE2021S1002 ZHU Yan-peng, HOU Xi-nan, MA Xiang-xiang, et al. Limit analysis of slope stability supported by framed prestressed anchor rods[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S1): 7–12. (in Chinese) doi: 10.11779/CJGE2021S1002
[2]	YANG X H, GUO N, ZHANG Z N, et al. Model test and Stability analysis of large high deposit body landslide under heavy rainfall[J]. Soil Mechanics and Foundation Engineering, 2022, 59(5): 467–474. doi: 10.1007/s11204-022-09838-z
[3]	吴刚, 冯德成. 装配式混凝土框架节点基本性能研究进展[J]. 建筑结构学报, 2018, 39(2): 1–16. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201802001.htm WU Gang, FENG De-cheng. Research progress on fundamental performance of precast concrete frame beam-to-column connections[J]. Journal of Building Structures, 2018, 39(2): 1–16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201802001.htm
[4]	苏俊霞, 郑静, 安孟康, 等. 拼装式锚杆(索)框架结构力学特征数值模拟与试验研究[J]. 铁道建筑, 2017, 57(10): 101–104. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201710027.htm SU Jun-xia, ZHENG Jing, AN Meng-kang, et al. Numerical simulation and experimental study on mechanical features of assembled anchor (cable) frame structure[J]. Railway Engineering, 2017, 57(10): 101–104. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201710027.htm
[5]	郑静, 安孟康, 苏俊霞, 等. 拼装式锚杆(索)框架现场试验研究[J]. 铁道建筑, 2020, 60(7): 93–97. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ202007023.htm ZHENG Jing, AN Meng-kang, SU Jun-xia, et al. Field test study on assembled anchor bolt(cable) frame[J]. Railway Engineering, 2020, 60(7): 93–97. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ202007023.htm
[6]	杨校辉, 郭楠, 张卫雄, 等. 一种节点连接部件以及框架预应力锚索支护结构: ZL 201920917783.8. [P]. 2020-05-19. YANG Xiao-hui, GUO Nan, ZHANG Wei-xiong, et al. The utility model relates to a node connecting part and a frame prestressed anchor cable support structure: ZL 201920917783.8. [P]. 2020-05-19. (in Chinese)
[7]	杨校辉, 郭楠, 张卫雄, 等. 一种基于型钢连接的预制构件以及装配式框架支护结构: ZL 201921087299.3. [P]. 2020-04-14. YANG Xiao-hui, GUO Nan, ZHANG Wei-xiong, et al. The utility model relates to a prefabricated component based on section steel connection and a fabricated frame support structure: ZL 201921087299.3. [P]. 2020-04-14. (in Chinese)
[8]	孙志明. 预制装配式边坡支护结构应用研究[D]. 石家庄: 石家庄铁道大学, 2019. SUN Zhi-ming. Application research on prefabricated slope supporting structure[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2019. (in Chinese)
[9]	ZHANG W X, LV W L, ZHANG J Y, et al. Energy-based dynamic parameter identification for Pasternak foundation model[J]. Earthquake Engineering and Engineering Vibration, 2021, 20(3): 631–643. doi: 10.1007/s11803-021-2043-6
[10]	FU J, LIANG J W, BA Z N. Model errors caused by rigid-foundation assumption in soil-structure interaction: a comparison of responses of a soil-structure-flexible foundation system and a rigid foundation system[J]. Bulletin of Earthquake Engineering, 2021, 19(1): 77–99. doi: 10.1007/s10518-020-00978-x
[11]	梅岭, 张太玥, 姜朋明. 基于Winkler弹性地基模型格构梁节点荷载分配研究[J]. 建筑科学, 2015, 31(7): 52–56. https://www.cnki.com.cn/Article/CJFDTOTAL-JZKX201507010.htm MEI Ling, ZHANG Tai-yue, JIANG Peng-ming. Study on load distribution coefficient of lattice beam node based on winkler elastic foundation model[J]. Building Science, 2015, 31(7): 52–56. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZKX201507010.htm
[12]	张太玥, 梅岭. 锚杆格构梁节点荷载分配研究与优化设计[J]. 水利水电技术, 2016, 47(1): 36–40. https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ201601008.htm ZHANG Tai-yue, MEI Ling. Study on nodal load allocation of anchor rod-lattice beam and its optimization design[J]. Water Resources and Hydropower Engineering, 2016, 47(1): 36–40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJWJ201601008.htm

施引文献(9)

期刊类型引用(4)

1.	钟紫蓝，史跃波，李锦强，赵密，杜修力. 考虑土体动力特征参数相关性的工程场地随机地震反应分析. 岩土力学. 2022(07): 2015-2024+2033 . 百度学术
2.	闫静茹，张郁山，阚文亮. 地震动场地调整系数研究. 地震学报. 2022(05): 783-796 . 百度学术
3.	李平，周楷，刘应慈，李玉影，朱胜. 场地抗震分类方法对比研究——以松原场地为例. 防灾科技学院学报. 2021(02): 39-45 . 百度学术
4.	周勇，丁海平，于彦彦. 基于反演基岩加速度的场地放大系数的探讨. 苏州科技大学学报(工程技术版). 2020(03): 1-5 . 百度学术