0.   引言

土体水分的赋存状态以及变化规律是土体工程性质、浅地表生态环境的重要影响因素^[1]。然而，由于土体所处环境的复杂性和土体本身的异质性，大规模、长距离的土体含水率原位观测仍存在诸多挑战。当前，土体含水率的主要原位测试方法包括时域反射法（TDR）、频域反射法（FDR）等^[2–5]。TDR方法通过测量电磁脉冲在土体中传播的速度计算土体含水率，可实现无损检测，较高测试精度（±1%），消耗人力少，易于携带、安装和操作，但TDR探针对环境条件敏感，在含盐量很高的土壤中可能造成一定的测试误差。FDR技术与TDR技术相似，FDR通过土体中传播电磁波的频率变化确定土体含水率。

近年来，凭借信息易于获取、环境友好以及易于拓展的测试装置，基于温度示踪方法的土体含水率反演逐渐得到关注^[6-8]。该类方法分为主动温度信息法（人为加热提供热源）和自然温度信息法（热量源于自然热量）两种。主动温度信息法在待测土体中注入人为热量、观测其温度响应，通过建立温度和含水率之间的关系来实现土体含水率的测试^[8]。Weiss^[9]论证了主动温度信息法估算土体含水率的可行性，Perzlmaier等^[10-11]则基于该方法定性区分了完全饱和、部分饱和以及完全干燥的土体。当用于加热的能源易于获取时，主动温度信息方法可以实现点式高精度测试并通过优化传感器布设方案实现较大范围测试^[12-13]。自然温度信息法通过观测土体在自然大气温度边界条件下的温度响应变化实现土体含水率的估算。Suzuki^[14]基于正弦温度上边界假设提出了用于描述热量传递的对流弥散方程解析解。Tabbagh等^[15]在包气带中应用了自然温度信息法计算土体含水率，Béhaegel等^[16]连续记录了14个月的自然温度信息，研究了土体含水率的长时间变化规律。McCallum等^[17]根据不同深度土体温度变化曲线提取的振幅和相移进行了热扩散系数的估算，获得了从小范围（数十厘米至数十米）至大范围（数百米至数千米）多尺度的土体热扩散系数。自然温度信息法方法涉及理论背景简明、测试系统要求低，在实现大规模、长距离的含水率原位观测中具有重要的潜力。

分布式光纤温度感测技术（fiber optic distributed temperature sensing，FO-DTS）连续测试的特点使得基于自然温度信息方法进入了新的阶段^[18]。Steele-Dunne等^[19]利用水平布设的测温光缆，并基于FO-DTS获取的高空间分辨率自然温度信息，验证了浅表10 cm范围内土体平均含水率连续观测的可行性。Dong等^[20-21]进一步量化了FO-DTS技术在获取自然温度信息中存在的光缆埋深不确定性、测温精度不确定性以提高估算土体含水率的可靠性。Halloran等^[22]降低了土体导热系数在空间上的异质性对土体含水率估算的影响。Cao等^[23]利用统计模型实现了土体含水率的简便估算，并总结不同地表覆盖物下土体含水率的变化规律。值得注意的是，基于FO-DTS的被动温度信息法目前可以是实现水平布设光缆条件下的土体含水率估算，但通常局限与单个深度点到地表或有限深度点之间的土体平均含水率的观测。由于自然温度信息受昼夜更替、天气等因素的影响复杂多变，精细化观测在研究中愈发重要。这就需要开展在深度方向上实现连续测试和如何实现多尺度测试的相关研究。总体上，利用FO-DTS实现基于自然温度信息法的含水率估算研究在岩土工程领域的研究中才刚起步，国内尚未见报道。

本研究利用FO-DTS，提出了基于高时空分辨率自然温度信息的土体含水率的新方法，实现了浅地表土体的含水率原位测试，获得了不同深度含水率在时间上变化规律，探讨了土体含水率变化与天气变化之间的耦合关系，以期为该类新技术的原位长距离应用提供科学支撑。

1.   理论方法

1.1   分布式光纤温度感测技术

分布式光纤感测技术（distributed fiber optic sensing，DFOS）是近年来快速发展的一类新型感测技术，该类技术集光传感与传输为一体，利用光纤中布里渊、拉曼、瑞利和布拉格等散射和反射光的特征量，可对光纤沿线外界环境引起的应变、温度和振动等物理量进行连续分布式获取。FO-DTS主要利用拉曼散射光进行测试，其基本原理：一束泵浦光注入光纤后，光子和光纤分子发生的非弹性碰撞，入射光发生背向散射，产生拉曼散射光。根据散射光中心频率的不同，将中心频率大于入射光中心频率的散射光称之为反斯托克斯光，将中心频率小于入射光中心频率的散射光称之为斯托克斯光。反斯托克斯光和斯托克斯光的强度比值是有关温度的函数，可表示为

式中：R(T)为待测温度的函数；I_F为反斯托克斯光强；I_S为斯托克斯光强；v_F为反斯托克斯光频率；v_S为斯托克斯光频率；c为真空中的光速；v为拉曼平移量；h为普朗克常量；K为波尔兹曼常数；T为绝对温度。

1.2   温度时间序列分析方法

对于浅地表土体，大气温度的变化会导致土体温度的变化，而土体的含水率会影响土体温度变化的快慢：不同深度的土体，含水率的差异导致土体热扩散系数不同。当表面热量向下传递时，不同含水率的土体会呈现出对温度的不同响应（图 1，Halloran等^[15]）。原黎明等^[24]提出通过提取不同深度相应温度变化曲线的振幅和相位计算土体热扩散率的方法：

图  1  基于FO-DTS的自然温度信息土体含水率的估算方法

Figure  1.  Estimation method for soil moisture content based on FO-DTS natural temperature information

下载: 全尺寸图片 幻灯片

式中：K为土体热扩散率（m²/s）；z₁，z₂分别为相邻两个土体深度（m）；A₁，A₂分别为相邻两个土体深度地温正弦波动的振幅（℃）；ϕ₁，ϕ₂分别为相邻两个土体深度地温正弦波动的初始相位（rad）；ω为地球自转的角速度（rad/s），ω = 2π/p，p为地温的日变化周期（p = 24×60×60 s）。假设地温符合正弦波动，则可以通过计算两个不同深度的日地温变化振幅比和相位差来得到土体热扩散系数。需要注意的是，随深度的增加，土体温度日变化振幅逐渐衰减，通常只根据日周期的温度数据计算0~0.5 m土体的热扩散系数^[24]。

降雨、气温快速变化等事件会导致地温日周期变化不完全符合正弦波动。对此，可采用Matlab内置的bandpass函数提取温度变化曲线中的振幅和相位信息，根据具体情况使用带通滤波器对输入温度信号进行滤波，并用最小阶滤波器补偿滤波器引入的延迟。

1.3   土体热扩散系数与含水率的关系

土孔隙中的水与空气相比具有较高的导热系数和比热容，因此不同含水率土体具有不同的热扩散系数。随着土体体积含水率的增加，土体热扩散系数先快速增加，达到峰值后缓慢减小，表现近似对数正态的相关关系^[25]。在此基础上，Arkhangel’Skaya等^[26]分析证明了对数正态函数预测土体含水率与热扩散系数关系的通用模型的准确性，如下所示：

式中：θ为体积含水率，θ = w·ρ_d，w为质量含水率，ρ_d为土体干密度；K₀为干土热扩散系数（m²/s）；θ₀为测到的热扩散系数最大值所对应的含水率（cm³/cm³）；a为测到的热扩散系数最大值与干土热扩散系数的差值（m²/s）；b为k(θ)曲线峰值的一半对应的含水率范围。

式（3）中的参数可以通过拟合实测K(θ)曲线获得，并且与土体成分、干密度等因素密切相关。本研究中，按质量比3︰1配制细砂和高岭土混合的模型土，控制干密度1.8 g/cm³，在不同含水率条件下（体积含水率0%~34%，共11组），使用美国METER公司TEMPOS热特性分析仪的SH-3探针测试土体热扩散系数，获得该混合土的含水率和热扩散系数关系（图 2）。基于式（3）拟合得K₀ = 2.76，a = 8.35，θ₀ = 14.98，b = 0.89，R² = 0.95。

图  2  混合土热扩散系数与含水率关系曲线

Figure  2.  Relation curves of thermal diffusion coefficient and moisture content of mixed soil

下载: 全尺寸图片 幻灯片

2.   现场试验

在南京大学仙林校区开展了基于模型土的原位试坑试验。通过将0.9 mm Hytrel紧包光缆缠绕在PVC管上的方式制作了螺旋传感器，提高FO-DTS方法的空间分辨率。试坑的长宽高分别为70 cm×70 cm×25 cm，螺旋管的有效感测深度范围为1~22 cm，在深度为7.5 cm处放置TDR传感器（测试精度±1%），同步记录土体含水率信息，采用分层控制土体密度的方法均匀回填1.3节所述模型土，干密度为1.8 g/cm³。

FO-DTS的解调设备采用当前国际先进的英国Silixa Ultima-M MK2型DTS光纤测温仪（简称Ultima DTS），其理论测温分辨率0.01℃，精度为0.1℃，空间分辨率达0.254 m，时间采样间隔为10 s，最大测量距离为10 km。使用冷水浴和热水浴进行测量温度校准降低环境温度波动的影响，进一步提高温度观测稳定性。试坑所用螺旋管最终实现了0.1 cm空间分辨率、0.1℃温度分辨率的垂向连续温度观测。Ultima DTS记录螺旋传感器不同深度温度随时间的变化，持续30 d（2022年2月20—3月20日），并基于式（2），（3）估算不同深度的土体含水率。

图  3  基于FO-DTS自然温度信息法实验示意图

Figure  3.  Experimental diagram of FO-DTS-based natural temperature information method

下载: 全尺寸图片 幻灯片

3.   测试结果与分析

3.1   温度的时空分布

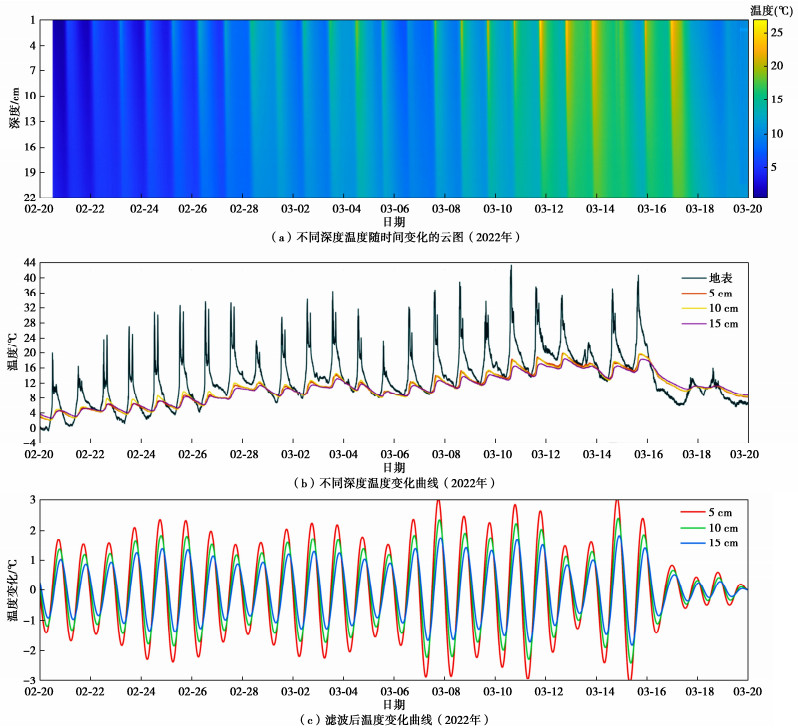
测试期为冬季向春季的过渡期，环境温度波动上升，浅表各层温度均在波动上升。测试期间，地面以下1~22 cm内土体温度随时间的连续变化结果见图 4（a）。可以看到，浅层土体受到环境昼夜温度变化的影响，浅表各深度均出现日周期性高温、低温交替现象。在日周期中，地表最先响应环境温度，然后能量逐渐向下层土体扩散，随深度的增加，土体的高温极值依次降低、低温极值依次增加，即上层土体温度变化范围大于下层；且上层达到高温和低温温度极值的时间早于下层。以地下5，10，15 cm 3个深度的温度随时间变化曲线为例（图 4（b）），温度日变化曲线近似呈现正弦波动特征。利用bandpass函数对温度变化曲线滤波处理后的结果见图 4（c），可以看到上层土体与环境温度的耦合性高，即上层土体温度变化的振幅大于下层，达到极值的相位上层早于下层。

图  4  云图和变化曲线

Figure  4.  Cloud map of temperature change at different depths over time

下载: 全尺寸图片 幻灯片

3.2   土体含水率的时空分布

提取5，10，15 cm处滤波后温度曲线的振幅比（A₁/A₂）和相位差（ϕ₁–ϕ₂）代入式（2）中可以计算得到的7.5，12.5 cm埋深处土体的热扩散系数，并根据拟合得到的土体热扩散系数-含水率关系（式（3））分别计算得到对应深度处含水率。图 5给出了计算得到的7.5，12.5 cm处含水率变化以及7.5 cm处TDR获得的日平均含水率。

图  5  不同深度土体含水率随时间变化图

Figure  5.  Variation of soil moisture with time at different depths

下载: 全尺寸图片 幻灯片

整体上，FO-DTS体积含水率平均值为12.45%，与TDR12.48%的结果差距在5%以内。值得注意的是，FO-DTS含水率对天气的响应幅度敏感度明显高于TDR传感器。这一方面反应了TDR传感器在含水率极值端观测不确定性难以限制的特点^[27]，另一方面也反应了滤波算法在复杂环境下具有放大土体温度的实际变化的可能性。在快速降雨事件中，由于土体垂向的热量传递中热传导形式和热对流形式耦合复杂，造成土体含水率的观测不确定性的增加。在极端寒潮事件下，由于地表蒸发锐减，含水率基本维持稳定，温度变化幅度的锐减（图 4（b））可能造成估算误差随之增加。

基于自然温度信息获得的不同深度含水率对环境变化均有较好的响应。在测试期间，发生了3次降雨事件和一次寒潮事件。2月20日—3月4日，天气以多云和晴天为主，地表蒸发条件好，7.5，12.5 cm处含水率整体不断下降；其中，2月27日出现少量降雨，7.5 cm层土体含水率微弱上升，但天气变化影响能量的向下传递，计算得到12.5 cm含水率有较明显的增加，且12.5 cm层受到少量降雨事件的影响晚于7.5 cm层。3月5日—3月12日，12.5，7.5 cm层土体含水率计算结果均出现异常值，且12.5 cm层受到寒潮事件的影响晚于7.5 cm层。3月13日和3月14日有中雨；3月17日有大雨。12.5，7.5 cm层土体含水率均有明显上升，且12.5 cm层受到中量降雨事件的影响晚于7.5 cm层，而受到影响的程度弱于7.5 cm层。

总体上，FO-DTS获得的含水率12.5 cm处略高于7.5 cm处，且对天气事件的响应也存在滞后现象，这与较深的位置与环境热交换较弱，含水率较稳定且不易散失有关，FO-DTS含水率观测结果可以较好地反映浅表土体含水率变化。

4.   讨论

FO-DTS解调仪测试结果的空间分辨率通常为0.25~0.4 m，本研究中将测温光缆均匀缠绕在直径为0.2 m的PVC管上，可以将其测试的空间分辨率提高至1 mm，从而获得浅地表 0~22 cm内连续的温度变化（图 4（a））。选取5，10，15 cm进行分析，测试结果表明，通过对土体自然温度信息的相位和振幅提取，可以有效反演土体不同深度的含水率变化。而当深度大于0.5 m时，土体温度日变化振幅显著减小^[24]，无法呈现显著的温度正弦波动，因此本文基于FO-DTS的自然温度信息法主要适用于地表 0~0.5 m内土体含水率的估算。

另一方面，分布式光纤温度测试技术则可以使这种基于温度信息的含水率估算方法实现多尺度的应用。具体来说，FO-DTS的测试范围通常为0~10 km，因此通过适当的布设，即可在该范围内实现土体含水率的估算。在实际应用中，只需根据测试范围需求，将光纤埋设于浅表不同深度的土体中，提取不同深度土体温度随时间的变化，即可长期有效地获取多尺度区域范围内土体含水率的变化，如长距离、大范围的含水率估算（图 6（a））或局部的、小尺度的精细化监测（图 6（b）），实现多尺度的浅表土体含水率估算。考虑到土体含水率与土体工程性质（力学性质、水理性质等）关系密切^[28]，快速掌握浅表土体含水率变化，对岩土体稳定性及灾害防治、环境工程地质、生态工程地质等研究和实践具有重要意义。

图  6  基于分布式温度信息的土体含水率多尺度估算示意图

Figure  6.  Multi-scale estimation of soil moisture content based on distributed temperature information

下载: 全尺寸图片 幻灯片

此外需要注意的是，本文中计算得到的土体含水率实际为体积含水率，由于已知土体干密度，可将其转化为质量含水率。但原位监测或大尺度监测时，土体干密度通常无法准确获得，因此也可采用体积含水率进行分析。

5.   结论与展望

本文提出了一种基于分布式温度信息的土体含水率多尺度估算方法，通过原位试验，验证了该方法在长期监测的可靠性，揭示了不同天气条件下土体含水率的变化规律。得到3点主要结论。

（1）浅层土体自身温度信息能够很好地反映其在不同天气条件下含水率变化，如当多云或者晴朗时土体含水率下降；当有降雨时，土体含水率上升，而上升幅度与降雨量有较好的相关性；当有寒潮时，土体含水率有明显异常。

（2）下层土体水分容易富集，使下层土体含水率高于上层；而下层土体受到降雨、寒潮等事件的影响小于上层，且具有显著的滞后性。

（3）基于FO-DTS的自然温度信息法可以对小范围至大范围多尺度的土体含水率进行长期有效监测，对研究多尺度浅地表土-水相互作用、地质和岩土工程防灾减灾具有重要意义。