考虑封底效应的圆形围堰渗流场解析解及应用

黄娟; 和振; 余俊; 和炜杰

doi:10.11779/CJGE20221101

考虑封底效应的圆形围堰渗流场解析解及应用 English Version

中南大学土木工程学院, 湖南长沙 410075

基金项目:

国家自然科学基金项目 52078496

详细信息

作者简介:
作者简介：黄娟(1977—)，女，博士，副教授，主要从事隧道与地下工程施工力学和动力学方面的教学和研究。E-mail：210057@csu.edu.cn

通讯作者:
余俊, E-mail: jjyy1017@163.com

中图分类号: TU43
计量
- 文章访问数: 348
- HTML全文浏览量: 42
- PDF下载量: 102
出版历程
- 收稿日期: 2022-09-05
- 网络出版日期: 2023-03-13
- 刊出日期: 2023-11-30

Analytical solutions and application of circular cofferdams considering backseal effects

School of Civil Engineering, Central South University, Changsha 410075, China

摘要

摘要: 将圆形围堰周围渗流场分为4个区域，用分离变量法分别得到柱坐标系下4个区域的水头分布级数解形式，结合区域间的连续条件，并利用贝塞尔函数正交性得到考虑封底效应的圆形围堰稳态渗流场解析解。该解析解能求解成层土情况下围堰涌水量及封底层渗流水压力，并能退化到各向同性土层中围堰未封底情况。通过与数值计算结果以及其他近似法计算结果的对比，证明了该解析解的正确性及有效性。基于解析解，分析了封底层渗流水压力分布规律，结合工程实例探讨了考虑渗流影响的封底层失稳破坏规律。结果表明：渗流作用下封底层所受水压力并非均匀分布，而是呈现中心小四周大的分布形式；封底层渗透系数及厚度会显著影响渗流水压力的大小及分布。
- 圆形围堰渗流 /
- 解析解 /
- 封底层 /
- 渗流量 /
- 渗流水压力
Abstract: The seepage fields around a circular cofferdam are divided into four regions, and the fractional variable method is used to obtain the sequence solutions of the water head distribution in the four regions under the cylindrical coordinate system, combined with the continuous conditions between the regions, and the analytical solutions of the steady seepage fields of the circular cofferdam are obtained by using the bessel function orthogonality. The correctness and effectiveness of the analytical solutions are proved by comparison with the numerical results and those by other approximate methods. The analytical solutions can be used to solve the water inflow of the cofferdam and the water pressure of the concrete at the bottom of the cofferdam in the case of double-layer soil, and can be degraded to the case of the cofferdam without the bottom of the isotropic soil. Based on the analytical solutions, the distribution laws of the seepage water pressure of subsealing concrete are analyzed, and the instability failure laws of subsealing concrete considering seepage influences are discussed through an engineering example. The results show that the water pressure on the concrete under seepage is not uniformly distributed, but in the form of being small in the center and large in the periphery. The permeability coefficient and thickness of the concrete at the bottom of the seal significantly affect the magnitude and distribution of the seepage water pressure.
- seepage of circular cofferdam /
- analytical solution /
- subsealing concrete /
- seepage quantity /
- seepage pressure

HTML全文

0. 引言

围堰作为一种临时性围护结构，广泛应用于桥梁工程、水工结构、给排水工程结构的基础建设中。其作用是防止水进入施工位置，以便在围堰围成的基坑内排水、开挖和修筑基础等工程设施。其中，圆形(轴对称)围堰是比较常见的围堰类型。研究围堰及其基础的渗流、封底层的稳定性，防止围堰发生失稳、堰基渗透破坏^[1]，是围堰设计的重要内容。

目前对围堰渗流问题的研究多为未封底情况下开挖面水力坡度、渗流量等渗流场参数的计算，方法以数值方法和解析法为主。数值方法已经比较成熟，Madanayaka等^[2]基于数百个二维和三维有限元模拟，开发和验证了估计方形和矩形围堰的流量和出口水力梯度的简单表达式。Benmebarek等^[3]采用FLAC软件对水平均匀各向同性和各向异性砂质地基中板桩围堰的渗透破坏和板桩旋转失稳破坏机理进行了研究，归纳出了两种破坏形式的出现情况及特点。Tanaka等^[4]对围堰内土体三维渗流破坏进行了不同工况试验研究，并对土体进行了有限元渗流分析和土体抗渗流破坏稳定性分析，指出三维渗流比二维渗流对渗流破坏稳定性的影响更大。解析法能够将地下水初始条件、水位变化等因素融入求解过程，通过一个函数表达式将各因素表达出来，具备定量分析和定性分析的优点^[5]，现有渗流解析解多针对长宽比较大的狭长型围堰，这种情况下可将渗流分析变为一个二维问题进行求解，Kavvadas等^[6]通过对板桩基坑周围土体二维稳态流动的广泛参数有限元分析结果进行多元回归拟合, 得到了地下水位以下板式开挖的地下入渗量、渗流出口梯度及截水单元上水力分布的近似封闭表达式。Banerjee等^[7]利用连续保角映射的方法，得到了矩形双壁围堰稳定渗流问题的隐式解析解。Bereslavskii^[8]基于保角变换法给出了恒定水位下单个板桩墙周围稳态渗流场的解析解答。目前关于圆形围堰渗流解析研究的相关文献较少，Neveu^[9]将格林函数和图解法相结合，给出了一种估计流量的图形解。然而，它并没有给出出口水力梯度的解，其适用性局限于各向同性条件。Madanayak等^[10]对分段法（MoF）进行改进，提出了可估算圆形围堰开挖面水力坡度及渗流量的分段法，该种方法假定板桩端等势线垂直，获得的是一种近似解。

本文建立轴对称柱坐标下三维渗流模型，推导出考虑封底效应的圆形围堰稳态渗流场解析解，该解析解考虑了成层土，能准确计算围堰渗流场水头、开挖面水力坡度、涌水量，且能对封底情况下封底层的渗流量及所受渗透力进行计算分析，可为围堰稳定性分析及封底层厚度优化设计提供一定的参考。

1. 圆形围堰稳态渗流场解析解

1.1 计算模型及基本假定

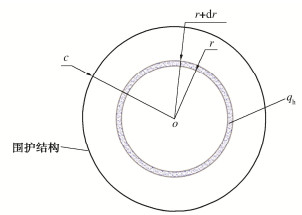
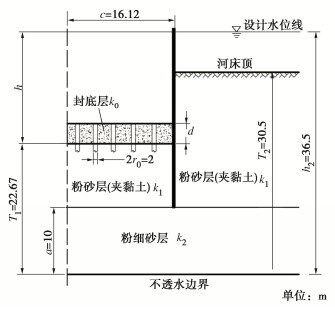
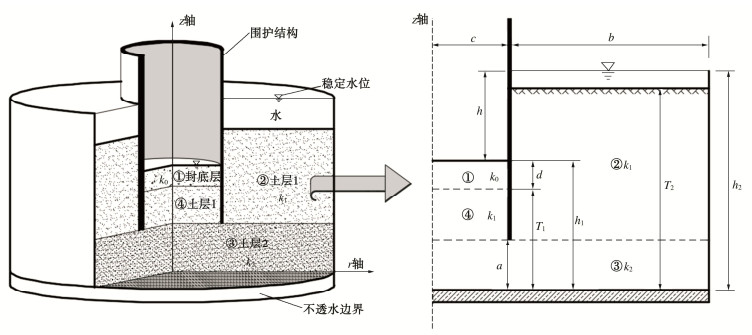
以圆形围堰中心为Z轴，围堰底部不透水层顶面为r轴，选取围堰周围有限区域圆柱状土体，建立轴对称三维渗流解析模型，如图 1：柱状区域①为封底层，渗透系数k₀；围护结构内柱状区域④、围护结构外柱环区域②为土层1，渗透系数k₁；围护结构底部至不透水边界的柱状区域③为土层2，渗透系数k₂。围堰半径为c，封底层厚度为d，围堰外透水土层厚度为T₂，围堰内透水土层厚度为T₁，围护结构至模型边界距离为b，至底部不透水边界距离为a。围堰内侧及外侧稳定水位分别为h₁，h₂，内外侧水头差为h。

图 1 围堰渗流模型

Figure 1. Model for seepage around cofferdam

下载: 全尺寸图片幻灯片

做以下假定：①土体各向同性；②地下水渗流符合达西定律；③围堰处于稳定渗流状态；④围护结构不透水；⑤含水层下部土层为不透水边界。

封底层按多孔介质考虑，根据达西定律，区域①、区域②、区域③和区域④中的渗流在柱坐标系下满足平衡方程^[13]：

$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial {H}_{i}}{\partial r}\right)+\frac{{\partial }^{2}{H}_{i}}{\partial {z}^{2}}=0{\text{ }}（i=1, 2, 3, 4）。$

(1)

式中：H₁，H₂，H₃，H₄分别为区域①、区域②、区域③和区域④的总水头，水头计算基准为透水层底面。

区域①边界条件如下：上边界( $z = {h_1}$ )， ${H_1} = {h_1}$ ；外边界( $r = c$ )， $\partial {H_1}/\partial r = 0$ 。

区域②边界条件如下：上边界( $z = {T_2}$ )， ${H_2} = {h_2}$ ；外边界( $r = b + c$ )，当b取值很大时可近似看为 $\partial {H_2}/\partial r = 0$ 。

区域③边界条件如下：下边界( $z = 0$ )， $\partial {H_3}/\partial z = 0$ ；外边界( $r = b + c$ )， $\partial {H_3}/\partial r = 0$ 。

区域④边界条件如下：外边界( $r = c$ )， $\partial {H_4}/\partial r = 0$ 。

各区域间满足连续条件：

$\left. {\begin{array}{*{20}{l}}{{H}_{1}|}_{z={T}_{1}}={{H}_{4}|}_{z={T}_{1}}\;\;\;\;\;\;\;(0\le r < c{\text{)}}{\text{，}}\\ {{k}_{0}\frac{\partial {H}_{1}}{\partial z}|}_{z={T}_{1}}={{k}_{1}\frac{\partial {H}_{4}}{\partial z}|}_{z={T}_{1}}{\text{(}}0\le r\le c{\text{)}}{\text{，}}\end{array}} \right\}$

(2)

$\left. {\begin{array}{*{20}{l}}{{H}_{4}|}_{z=a}={{H}_{3}|}_{z=a}\;\;\;\;\;\;\;(0\le r < c{\text{)}}{\text{，}}\\ {{k}_{1}\frac{\partial {H}_{4}}{\partial z}|}_{z=a}={{k}_{2}\frac{\partial {H}_{3}}{\partial z}|}_{z=a}{\text{(}}0\le r\le c{\text{)}}{\text{，}}\end{array}} \right\}$

(3)

$\left. {\begin{array}{*{20}{l}}{{H}_{2}|}_{z=a}={{H}_{3}|}_{z=a}\;\;\;\;\;\;\;(c\le r < b+c{\text{)}}{\text{，}}\\ {{k}_{1}\frac{\partial {H}_{2}}{\partial z}|}_{z=a}={{k}_{2}\frac{\partial {H}_{3}}{\partial z}|}_{z=a}{\text{(}}c\le r\le b+c{\text{)}}。\end{array}} \right\}$

(4)

1.2 渗流场求解

运用分离变量法^[13]分别求解四区域水头表达式。

对柱状区域①，令 $H_1^* = {H_1} - {h_1}$ ，将非齐次边界条件转化为齐次边界条件，则区域①的渗流平衡方程转化为

$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial H_1^*}}{{\partial r}}} \right) + \frac{{{\partial ^2}H_1^*}}{{\partial {z^2}}} = 0。$

(5)

设式（5）有变量分离的形式解

$H_1^*(r, z) = {R_1}(r){Z_1}(z)。$

(6)

将式（6）代入式（5）中得

$- \frac{1}{{{Z_1}}}\frac{{{\partial ^2}{Z_1}}}{{\partial {z^2}}} = \frac{{\frac{{{\partial ^2}{R_1}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {R_1}}}{{\partial r}}}}{{{R_1}}} = - {\lambda ^2}。$

(7)

式中： $\lambda$ 为分离常数。

由式（7）得到

$\frac{{{\partial ^2}{Z_1}}}{{\partial {z^2}}} - {\lambda ^2}{Z_1} = 0{\text{，}}$

(8)

$\frac{\partial^{2} R_{1}}{\partial r^{2}}+\frac{1}{r} \frac{\partial R_{1}}{\partial r}+\lambda^{2} R_{1}=0 。$

(9)

当 $\lambda = 0$ 时，式（8），（9）的解分别为

${Z_1}(z) = {a_0} + {b_0}z{\text{，}}$

(10)

${R_1}(r) = {c_0}\ln r + {d_0}。$

(11)

当 $\lambda \ne 0$ 时，式（8），（9）的解分别为

${Z_1}(z) = {a_1}\sinh (\lambda z) + {b_1}\cosh (\lambda z){\text{，}}$

(12)

${R_1}(r) = {c_1}{{{\text{J}}}_0}(\lambda r) + {d_1}{{{\text{Y}}}_0}(\lambda r)。$

(13)

式（10）~（13）中： ${a_0}$ ， ${b_0}$ ， ${c_0}$ ， ${d_0}$ ， ${a_1}$ ， ${b_1}$ ， ${c_1}$ ， ${d_1}$ 为待定常数； ${{{\text{J}}}_0}$ (x)， ${{{\text{Y}}}_0}$ (x)分别为零阶第一类、第二类贝塞尔函数。

${{{\text{Y}}}_0}$ 在u = 0处不是有界的，故必须取D₁=0，结合外边界条件，确定C₀ = 0，且 ${{{\text{J}}}_1}(\lambda c) = 0$ ，可见分离常数为 ${\lambda _n}(n = 0, 1, 2, \cdots )$ 的集合， ${\lambda _0} = 0$ ， ${\lambda _n}c(n = 1, 2, 3, \cdots )$ 为零阶第一类贝塞尔函数 ${{{\text{J}}}_1}$ (x)的第n个正零点。

结合区域①上边界条件，确定 ${a_0} = - {b_0}{h_1}$ ， ${b_1} = 0$ ，整合待定常数，可得区域①水头的一般解：

${H_1}(r, z) = {h_1} + {A_0}(z - {h_1}) + \sum\limits_{n = 1}^\infty {{A_n}\sinh {\lambda _n}(z - {h_1}){{{\text{J}}}_0}({\lambda _n}r} )。$

(14)

式中： ${A_0}$ ， ${A_n}$ 为整合后的待定系数。

区域②为柱环区域，故变量分离后所得贝塞尔方程的解为通解形式^[14]：

${R_2}(r) = {c_2}{{{\text{J}}}_0}({\lambda _m}r) + {d_2}{{{\text{Y}}}_{{\text{0}}}}({\lambda _m}r)。$

(15)

结合区域②内外侧边界条件得到：

$\left. {\begin{array}{*{20}{l}}{c}_{2}{{\text{J}}}_{1}({\lambda }_{m}c)+{d}_{2}{{\text{Y}}}_{1}({\lambda }_{m}c)=0{\text{，}}\\ {c}_{2}{{\text{J}}}_{1}[{\lambda }_{m}(b+c)]+{d}_{2}{{\text{Y}}}_{1}[{\lambda }_{m}(b+c)]=0。\end{array}} \right\}$

(16)

式中： ${c_2}$ ， ${d_2}$ 为非零待定常数，可知 ${\lambda _m}(m = 1, 2, 3, \cdot \cdot \cdot )$ 为满足下列行列式条件的集合。

$\left| {\begin{array}{*{20}{c}} \begin{gathered} {{{\text{J}}}_1}({\lambda _m}c) \hfill \\ {{{\text{J}}}_1}[{\lambda _m}(b + c)] \hfill \\ \end{gathered} &\begin{gathered} {{{\text{Y}}}_1}({\lambda _m}c) \hfill \\ {{{\text{Y}}}_1}[{\lambda _m}(b + c)] \hfill \\ \end{gathered} \end{array}} \right| = 0。$

(17)

求解式（17）确定 ${\lambda _m}$ ，由此可得到区域②水头的一般解：

${H_2}(r, z) = {h_2} + {B_0}(a - {T_2}) +$

$\sum _{m=1}^{\infty }{B}_{m}\mathrm{sinh}{\lambda }_{m}(a-{T}_{2})\left({{\text{J}}}_{0}({\lambda }_{m}r)-\frac{{{\text{J}}}_{1}({\lambda }_{m}c)}{{{\text{Y}}}_{1}({\lambda }_{m}c)}{{\text{Y}}}_{0}({\lambda }_{m}r)\right){\text{ }}。{\text{ }}$

(18)

式中： ${B_0}$ ， ${B_m}$ 为待定常数。

区域③为齐次边界条件，可直接用分离变量法求解，参照区域①求解步骤，代入边界条件，可得水头的一般解：

${H_3}(r, z) = {C_0} + \sum\limits_{i = 1}^\infty {{C_i}\cosh {\lambda _i}a{{{\text{J}}}_0}} ({\lambda _i}r) 。$

(19)

式中： ${C_0}$ ， ${C_i}$ 为待定常数， ${\lambda _i}$ 为区域③的分离常数，且 ${\lambda _i}(b + c)(i = 1, 2, 3, \cdots )$ 为零阶第一类贝塞尔函数 ${{{\text{J}}}_1}$ (x)的第i个正零点。

同理，对区域④进行求解，带入边界条件后，得到水头表达式：

${H_4}(r, z) = {E_0} + {D_0}z +$

${\text{ }}{\displaystyle \sum _{n=1}^{\infty }({D}_{n}\mathrm{cosh}{\lambda }_{n}z+{E}_{n}\mathrm{sinh}{\lambda }_{n}z){{\text{J}}}_{0}({\lambda }_{n}r)}{\text{ }}。$

(20)

式中： ${E_0}$ ， ${D_0}$ ，D_n，E_n为整合后的待定常数。根据区域①和区域④连续条件（2），建立等式：

${h_1} - {A_0}d - \sum\limits_{n = 1}^\infty {{A_n}\sinh {\lambda _n}d{{{\text{J}}}_0}(} {\lambda _n}r)$

$= {E_0} + {D_0}{T_1} + \sum\limits_{n = 1}^\infty {({D_n}\cosh {\lambda _n}} {T_1} + {E_n}\sinh {\lambda _n}{T_1}){{{\text{J}}}_0}({\lambda _n}r){\text{，}}$

(21)

${k_0}\left( {{A_0} + \sum\limits_{n = 1}^\infty {{\lambda _n}{A_n}\cosh {\lambda _n}d{{{\text{J}}}_0}} ({\lambda _n}r)} \right)$

$= {k_1}\left( {{D_0} + \sum\limits_{n = 1}^\infty {{\lambda _n}({D_n}\sinh {\lambda _n}} {T_1} + {E_n}\cosh {\lambda _n}{T_1}){{{\text{J}}}_0}({\lambda _n}r)} \right)。$

(22)

利用贝塞函数性质^[15]，由式（21），（22）可以得到未知系数的如下关系式：

${A_0} = \frac{{{k_1}}}{{{k_0}}}{D_0}{\text{，}}$

(23)

${E_n} = {\alpha _n} \cdot {D_n}{\text{，}}$

(24)

${E_0} = {h_1} - {D_0}\left( {\frac{{{k_1}}}{{{k_0}}}d + {T_1}} \right){\text{，}}$

(25)

$\alpha_{n}=\frac{-\sinh \lambda_{n} T_{1}-\tanh \lambda_{n} d-\frac{k_{0}}{k_{1}} \cosh \lambda_{n} T_{1}}{\cosh \lambda_{n} T_{1}-\tanh \lambda_{n} d+\frac{k_{0}}{k_{1}} \sinh \lambda_{n} T_{1}} 。$

(26)

为求解水头解析表达式中的所有未知系数，需要构造非齐次线性方程组，根据区域②、区域④与区域③交界处连续条件（2），（3），建立等式：

$\begin{array}{l}{C}_{0}+{\displaystyle \sum _{i=1}^{\infty }{C}_{i}\mathrm{cosh}{\lambda }_{i}a{{\text{J}}}_{0}}({\lambda }_{i}r)\\ =\left\{ {\begin{array}{*{20}{l}}{E}_{0}+{D}_{0}a+{\displaystyle \sum _{n=1}^{\infty }}{D}_{n}（\mathrm{cosh}{\lambda }_{n}a+\\ {\alpha }_{n}\mathrm{sinh}{\lambda }_{n}a）{{\text{J}}}_{0}({\lambda }_{n}r){\text{ }}（0\le r < c）{\text{ }}\\ {h}_{2}+{B}_{0}(a-{T}_{2})+{\displaystyle \sum _{n=1}^{\infty }{B}_{m}}\mathrm{sinh}{\lambda }_{m}(a-{T}_{2})\cdot \\ \left({{\text{J}}}_{0}({\lambda }_{m}r)-\frac{{{\text{J}}}_{1}({\lambda }_{m}c)}{{{\text{Y}}}_{1}({\lambda }_{m}c)}{{\text{Y}}}_{0}({\lambda }_{m}r)\right){\text{ }}（c\le r < b+c）\end{array}} \right.\end{array} {\text{，}}$

(27)

$\begin{array}{l}{\displaystyle \sum _{i=1}^{\infty }{k}_{2}{\lambda }_{i}}{C}_{i}\mathrm{sinh}{\lambda }_{i}a{{\text{J}}}_{0}({\lambda }_{i}r)\\ =\left\{ {\begin{array}{*{20}{l}}{k}_{1}[{D}_{0}+{\displaystyle \sum _{n=1}^{\infty }{\lambda }_{n}}{D}_{n}(\mathrm{sinh}{\lambda }_{n}a+\\ {\alpha }_{n}\mathrm{cosh}{\lambda }_{n}a){{\text{J}}}_{0}({\lambda }_{n}r){\text{] }}（{\text{0}}\le r\le c）{\text{ }}\\ {k}_{1}[{B}_{0}+{\displaystyle \sum _{n=1}^{\infty }{\lambda }_{m}{B}_{m}}\mathrm{cosh}{\lambda }_{m}(a-{T}_{2})\cdot \\ \left({{\text{J}}}_{0}({\lambda }_{m}r)-\frac{{{\text{J}}}_{1}({\lambda }_{m}c)}{{{\text{Y}}}_{1}({\lambda }_{m}c)}{{\text{Y}}}_{0}({\lambda }_{m}r)\right)]{\text{ }}（{\text{0}}\le r\le b+c）{\text{ }}\end{array}} \right.\end{array} 。$

(28)

式（27），（28）两边同时乘以r后积分，利用贝塞尔函数的性质，可得到待定常数的关系式：

$\frac{{{c^2}}}{2}{D_0} + \frac{{({b^2} + 2bc)}}{2}{B_0} = 0{\text{，}}$

(29)

$\frac{{[{E_0} + {D_0}a]{c^2} + [{h_2} + {B_0}(a - {T_2})]({b^2} + 2bc)}}{{{{(b + c)}^2}}} = {C_0}{\text{，}}$

(30)

${D_0} - \frac{{{k_2}}}{{{k_1}}}\frac{2}{c}\sum\limits_{i = 1}^\infty {{C_i}} {\lambda _i}\sinh {\lambda _i}a{{{\text{J}}}_0}({\lambda _i}r) = 0。$

(31)

式（27），（28）两边分别乘以 $r{{{\text{J}}}_0}({\lambda _i}r)$ ， $r{{{\text{J}}}_0}({\lambda _n}r)$ ， $r[{{{\text{J}}}_0}({\lambda _m}r) - {{{\text{Y}}}_0}({\lambda _m}r) \cdot {{{\text{J}}}_1}({\lambda _m}c)/{{{\text{Y}}}_1}({\lambda _m}c)]$ 在（0，b+c），（0，c），（c，b + c）区间分别积分，利用贝塞尔函数正交性，可得待定系数的关系式：

$({h_2} - {h_1})\frac{{c{{{\text{J}}}_1}({\lambda _i}c)}}{{{\lambda _i}}}$

$=\left\{ {\begin{array}{*{20}{l}}{D}_{0}\left[\frac{{c}^{2}}{{b}^{2}+2bc}(a-{T}_{2})-\left(\frac{{k}_{1}}{{k}_{0}}d+{T}_{1}\right)a\right]\frac{c{{\text{J}}}_{1}({\lambda }_{i}c)}{{\lambda }_{i}}+\\ {\displaystyle \sum _{n=1}^{\infty }{D}_{n}}(\mathrm{cosh}{\lambda }_{n}a+{\alpha }_{n}\mathrm{sinh}{\lambda }_{n}a){{\text{J}}}_{1}({\lambda }_{i}c){{\text{J}}}_{0}[{\lambda }_{i}(b+c)]\cdot \\ \frac{c{\lambda }_{i}}{{\lambda }_{i}^{2}-{\lambda }_{n}^{2}}+{\displaystyle \sum _{m=1}^{\infty }{B}_{m}\mathrm{sinh}{\lambda }_{m}(a-{T}_{2})\frac{2{\lambda }_{i}{{\text{J}}}_{1}({\lambda }_{i}c)}{{\text{π}}{\lambda }_{m}({\lambda }_{i}{}^{2}-{\lambda }_{m}{}^{2}){{\text{Y}}}_{1}({\lambda }_{m}c)}-}\\ {\displaystyle \sum _{i=1}^{\infty }{C}_{i}\mathrm{cosh}{\lambda }_{i}a\frac{{(b+c)}^{2}}{2}}{{\text{J}}}_{0}^{2}[{\lambda }_{i}(b+c)]\;\;\;\;\;(({\lambda }_{m}\ne {\lambda }_{i}){\text{ }}{\text{，}}\\ {D}_{0}\left[-\left(\frac{{k}_{1}}{{k}_{0}}d+{T}_{1}\right)a+\frac{{c}^{2}}{{b}^{2}+2bc}(a-{T}_{2})\right]\frac{c{{\text{J}}}_{1}({\lambda }_{i}c)}{{\lambda }_{i}}+\\ {\displaystyle \sum _{n=1}^{\infty }{D}_{n}}(\mathrm{cosh}{\lambda }_{n}a+{\alpha }_{n}\mathrm{sinh}{\lambda }_{n}a){{\text{J}}}_{1}({\lambda }_{i}c){{\text{J}}}_{0}[{\lambda }_{i}(b+c)]\cdot \\ \frac{c{\lambda }_{i}}{{\lambda }_{i}^{2}-{\lambda }_{n}^{2}}+{\displaystyle \sum _{m=1}^{\infty }{B}_{m}\mathrm{sinh}{\lambda }_{m}(a-{T}_{2})\frac{{{\text{J}}}_{0}({\lambda }_{m}c)}{\pi {\lambda }_{m}{{\text{Y}}}_{1}({\lambda }_{m}c)}-}\\ {\displaystyle \sum _{i=1}^{\infty }{C}_{i}\mathrm{cosh}{\lambda }_{i}a\frac{{(b+c)}^{2}}{2}{{\text{J}}}_{0}^{2}[{\lambda }_{i}(b+c)]\;\;\;\;\;({\lambda }_{m}={\lambda }_{i}{\text{) }}}{\text{；}}\end{array}} \right.$

(32)

$\left. {\begin{array}{*{20}{l}}{\displaystyle \sum _{n=1}^{\infty }{D}_{n}{\lambda }_{n}(\mathrm{sinh}{\lambda }_{n}a+{\alpha }_{n}\mathrm{cosh}}{\lambda }_{n}a)\frac{{c}^{2}}{2}{{\text{J}}}_{0}^{2}({\lambda }_{n}c)-\\ {\displaystyle \sum _{i=1}^{\infty }\frac{{k}_{2}}{{k}_{1}}{C}_{i}}{\lambda }_{i}\mathrm{sinh}{\lambda }_{i}a{{\text{J}}}_{1}({\lambda }_{i}c){{\text{J}}}_{0}[{\lambda }_{i}(b+c)]\frac{c{\lambda }_{i}}{{\lambda }_{i}^{2}-{\lambda }_{n}^{2}}=0{\text{ }}({\lambda }_{i}\ne {\lambda }_{n}){\text{，}}\\ {\displaystyle \sum _{n=1}^{\infty }{D}_{n}{\lambda }_{n}(\mathrm{sinh}{\lambda }_{n}a+{\alpha }_{n}\mathrm{cosh}}{\lambda }_{n}a)\frac{{c}^{2}}{2}{{\text{J}}}_{0}^{2}({\lambda }_{n}c)-\\ {\displaystyle \sum _{i=1}^{\infty }\frac{{k}_{2}}{{k}_{1}}{C}_{i}}{\lambda }_{i}\mathrm{sinh}{\lambda }_{i}a\frac{{c}^{2}{{\text{J}}}_{0}{}^{2}[{\lambda }_{i}(b+c)]}{2}=0{\text{ }}({\lambda }_{i}={\lambda }_{n}){\text{；}}\end{array}} \right\}$

(33)

$\left. {\begin{array}{*{20}{l}}{\displaystyle \sum _{m=1}^{\infty }{B}_{m}{\lambda }_{m}\mathrm{cosh}}{\lambda }_{m}(a-{T}_{2})\frac{2}{{{\text{π}}}^{2}{\lambda }_{m}{}^{2}}\left[\frac{1}{{{\text{Y}}}_{1}^{2}[{\lambda }_{m}(b+c)]}-\frac{1}{{{\text{Y}}}_{1}^{2}({\lambda }_{m}c)}\right]-\\ {\displaystyle \sum _{i=1}^{\infty }\frac{{k}_{2}}{{k}_{1}}{C}_{i}}{\lambda }_{i}\mathrm{sinh}{\lambda }_{i}a\frac{2{\lambda }_{i}{\mathrm{J}}_{1}({\lambda }_{i}c)}{{\text{π}}{\lambda }_{m}({\lambda }_{i}{}^{2}-{\lambda }_{m}{}^{2}){{\text{Y}}}_{1}({\lambda }_{m}c)}=0\;\;\;\;\;(({\lambda }_{m}\ne {\lambda }_{i}){\text{，}}\\ {\displaystyle \sum _{m=1}^{\infty }{B}_{m}{\lambda }_{m}\mathrm{cosh}}{\lambda }_{m}(a-{T}_{2})\frac{2}{{{\text{π}}}^{2}{\lambda }_{m}{}^{2}}\left[\frac{1}{{{\text{Y}}}_{1}^{2}[{\lambda }_{m}(b+c)]}-\frac{1}{{{\text{Y}}}_{1}^{2}({\lambda }_{m}c)}\right]-\\ {\displaystyle \sum _{i=1}^{\infty }\frac{{k}_{2}}{{k}_{1}}{C}_{i}}{\lambda }_{i}\mathrm{sinh}{\lambda }_{i}a\frac{{{\text{J}}}_{0}({\lambda }_{m}c)}{{\text{π}}{\lambda }_{m}{{\text{Y}}}_{1}({\lambda }_{m}c)}=0\begin{array}{cc}\begin{array}{cc}& \end{array}& \begin{array}{cc}& \end{array}\end{array}\;\;\;\;\;(({\lambda }_{m}={\lambda }_{i})。\end{array}} \right\}$

(34)

联立式（29）~（34）可构建非齐次线性方程组。由于方程为无穷阶线性方程组，必须将级数在第N项处截断，编制MATLAB计算程序求解方程组可计算出所有未知系数，进而得到各区域水头的级数解。

1.3 出口水力梯度

水力梯度就是沿地下水流方向上单位渗透途径上的水头损失^[16]。由式（14），可求得围堰开挖面任意一点处水力梯度为

${i_{{\text{e}}}} = - \frac{{\partial {H_1}}}{{\partial z}}\left| {_{z = {h_1}}} \right. = - \left( {{A_0} + \sum\limits_{n = 1}^\infty {{\lambda _n}} {A_n}{{{\text{J}}}_0}({\lambda _n}r)} \right)。$

(35)

1.4 开挖面渗流量

渗流量是设计任意形状围堰的关键参数，准确地估算流量至关重要。基于解析解可进一步得出开挖面渗流量表达式。渗流量为开挖面面积与渗流速度的乘积，依据渗流速度轴对称分布的性质。开挖面处渗流量可以理解为以z轴为中心的任意个圆环区域渗流量的叠加，如图 2。

图 2 涌水量计算示意图

Figure 2. Seepage quantity of unit circle

下载: 全尺寸图片幻灯片

其中单位圆环区域渗流量可表示为

${q_{{\text{h}}}} = {S_{{\text{h}}}}v = 2{{\text{π }}}{k_0}{i_{{\text{e}}}}r{{\text{d}}}r。$

(36)

式中： ${q_{{\text{h}}}}$ 为单位圆环渗流量； ${S_{{\text{h}}}}$ 为单位圆环面积； $v$ 为渗流速度； ${k_0}$ 为封底层渗透系数。对式（36）从0~c进行积分，即可得到开挖面处总渗流量。

$Q = - \int_0^c {2{{\text{π }}}{k_0}} \left( {{A_0} + \sum\limits_{n = 1}^\infty {{\lambda _n}} {A_n}{{J} _0}({\lambda _n}r)} \right)r{{\text{d}}}r$

$= - {{\text{π }}}{c^2}{k_0}{A_0} 。$

(37)

式中： $Q$ 为开挖面渗流量； ${A_0}$ ， ${A_n}$ 为水头函数中已确定的系数。开挖面沿围堰周长单位弧度的渗流量 $q$ 可表示为

$q = \frac{Q}{{2{{\text{π }}}c}} = - \frac{c}{2}{k_0}{A_0} 。$

(38)

2. 解析解的验证

2.1 水头对比验证

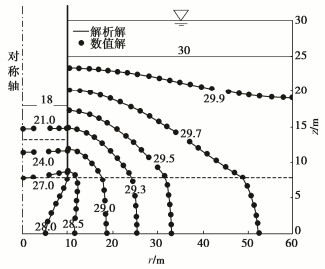
在实际圆形围堰中，渗流场可近似为轴对称的，所以分析可以在r-z平面内进行。利用解析解以及Plaxis2D软件计算圆形围堰渗流场水头，并将二者计算结果进行对比。解析解取级数项数N取60，经试算 $N \geqslant 60$ 时计算结果收敛。数值模型的边界条件同本文的解析模型。根据大卫登可夫等^[11]的研究，当模型半径与基坑半径比值等于6时（即 $(b + c)/c = 6$ ），可以认为基坑周围的水头分布和进入基坑的渗流量实际上与无限长边界相同。故在算例中围堰半径取10 m，围护结构至模型外边界距离取50 m，模型外边界设为不透水边界，土层渗透系数 ${k_1} = 6 \times {10^{ - 6}}{{\text{ m}}}/{{\text{s}}}$ ， ${k_2} = 2.4 \times$ ${10^{ - 5}}{{\text{ m/s}}}$ ，封底层渗透系数 ${k_0} = 5 \times {10^{ - 6}}{{\text{ m}}}/{{\text{s}}}$ ，具体计算参数如表 1。

表 1 围堰渗流模型的工程参数

Table 1. Engineering parameters of seepage model for cofferdam 单位: m

b	c	d	T₁	T₂	h₁	h₂	a
50	10	5	15	25	18	30	5

下载: 导出CSV

| 显示表格

建模时采用二维轴对称模型，以15节点的三角形单元对模型进行网格划分，对围护结构底部的网格局部加密。图 3显示了数值解与解析解水头分布对比情况，由图 3可知，本文所得解的计算结果与Plaxis2D软件数值计算结果吻合的很好，验证了本文所建模型解答的正确性。

图 3 围堰周围的水头分布

Figure 3. Distribution of water heads around cofferdam

下载: 全尺寸图片幻灯片

2.2 渗流量对比验证

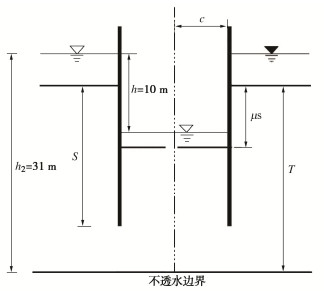
将本文解析公式计算的涌水量与数值解、文献[]中的MoF解和Neveu的图形解计算结果进行比较，计算参数取值与文献[]中一致，含水土层为单层各向同性条件（ ${k_0} = {k_1} = {k_2} = 5 \times {10^{ - 5}}{{\text{ m}}}/{{\text{s}}}$ ），围堰外水位高度31 m，围堰内外侧水头差h恒定为10 m，围护结构至模型外边界的距离取5倍围堰半径（ $b = 5c$ ），如图 4所示。

图 4 模型几何边界条件

Figure 4. Geometrical and boundary conditions of model

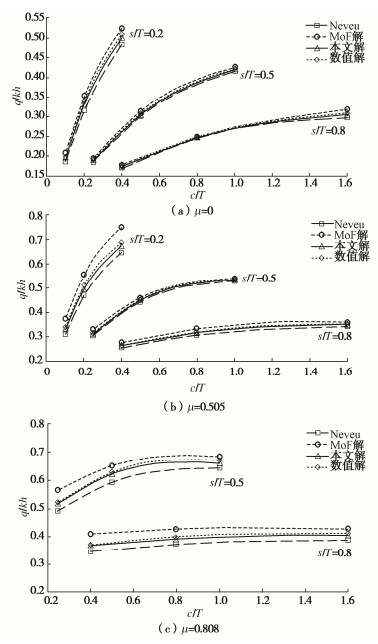
下载: 全尺寸图片幻灯片

分别表现了不同开挖深度情况下（ $\mu 为0，{\text{ }}$ $0.505，{\text{ }}0.808$ ），本文解析解与其他解析方法计算的开挖面涌水量对比结果。

图 5 开挖面涌水量对比结果

Figure 5. Comparison of analytical solutions, MoF and numerical model solutions by Madanayaka

下载: 全尺寸图片幻灯片

从整体上看，MoF解计算结果较大，Neveu解计算结果最小，数值解及本文解析解结算结果介于二者中间，且本文解析解计算结果略小于数值解。从误差看，开挖深度为0时( $\mu = 0$ )，围护结构插入深度较小(s = 0)的情况下，MoF解、Neveu解与数值解平均误差分别为6%，5%（ $s/T = 0.2$ ），本文解与数值解的误差为1.3%；另外两种情况( $s/T = 0.5$ 和 $s/T = 0.8$ )MoF解与数值解误差约为4%，6%，Neveu解与数值解的误差为3%，2%，本文解与数值解的误差为0.86%，0.65%。对于开挖深度 $\mu = 0.505$ ， $s/T = 0.2$ 时，MoF解与数值解平均误差为13%，Neveu解与数值解的误差为11%，本文解与数值解的误差为2%，另外两种情况其它两种解法与数值解的误差位于2%~4%，本文解与数值解误差约为0.4%，当开挖深度较大（ $\mu = 0.808$ ），MoF解、Neveu解与数值解的误差在 $s/T = 0.5$ 时分别约为7%，9.2%，在 $s/T = 0.8$ 时约为6.4%，6%，本文解与数值解在该两种情况下的误差约为1.1%。综上所述，相比于MoF解及Neveu解，本文解析解与数值解吻合得更好，具有较好的一致性，最大误差不超过2%。

3. 围堰封底层稳定性计算

3.1 封底层所受渗流水压力的计算分析

在流体力学中，根据伯努利方程，总水头由位置水头、压强水头、动能水头组成。稳态渗流情况下，动能水头为0。则总水头表达式为

$H = z + u/\rho g。$

(39)

水压力u用水头H表示的表达式为

$u = (H - z)\rho g。$

(40)

封底层底部水头可表示为

${H_4}(r, {T_1}) = {E_0} + {D_0}{T_1} +$

${\text{ }}{\displaystyle \sum _{n=1}^{\infty }(}{D}_{n}\mathrm{cosh}{\lambda }_{n}{T}_{1}+{E}_{n}\mathrm{cosh}{\lambda }_{n}{T}_{1}){{\text{J}}}_{0}({\lambda }_{n}r){\text{ }}。$

(41)

将式（41）代入式（40）得到封底层底部的水压力分布为

$u(r) = \left( {d - {D_0}\frac{{{k_1}}}{{{k_0}}}d + } \right.$

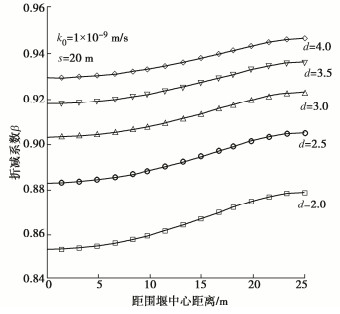
${\displaystyle \sum _{n=1}^{\infty }(}{D}_{n}\mathrm{cosh}{\lambda }_{n}{T}_{1}+{E}_{n}\mathrm{cosh}{\lambda }_{n}{T}_{1}){{\text{J}}}_{0}({\lambda }_{n}r)\cdot \rho g){\text{ }}。$

(42)

分析渗流时封底层厚度对封底层底部水压力的影响，定义封底层底部水压力折减系数 $\beta$ ：封底层底部作用的渗流水压力与围堰外水头作用于封底层底部的静水压力之比。

基本参数设置：围堰半径r =25 m，围护结构至外边界的距离b=100 m，围堰外透水层厚度T₂=25 m，土层渗透系数 ${k_1} = {k_2} = k = 1 \times {10^{ - 5}}{{\text{m/s}}}$ ，封底层渗透系数 ${k_0} = 1 \times {10^{ - 7}}{{\text{m/s}}}$ 围堰外水位高度h₂=30 m，围堰底部水位高度h₁=15 m。围护结构插入深度s=15 m，封底层厚度d分别取2.0，2.5，3.0，3.5，4.0 m。封底层厚度对水压力折减系数的影响曲线如图 6所示。结果表明：其他条件一定，随距围堰中心距离的增大，折减系数逐渐增大但增加的速率放缓；当封底层厚度增大，折减系数逐步增大，增长速率同样逐渐放缓。由此可见，渗流作用下，封底层底部所受水压力有一定程度的折减，折减程度随封底层厚度的增大而减小，且水压力并非均匀分布，而是呈现中心小四周大的分布形式。

图 6 水压力分布图

Figure 6. Distribution of seepage pressure

下载: 全尺寸图片幻灯片

3.2 渗流影响下的封底层失稳破坏判定公式

当封底层自重以及封底层与钢护筒间的黏聚力无法抵抗封底层下方的水压力作用时，封底层将会发生失稳破坏，图 7为封底层所受水压力以及摩阻力示意图，根据《钢围堰工程技术标准：GB/T51295—2018》，封底层失稳破坏极限平衡方程可表示为

${K_1}(G + {N_{{\text{u}}}}) \geqslant P。$

(43)

图 7 计算参数图

Figure 7. Computational parameters

下载: 全尺寸图片幻灯片

式中：K₁钢围堰的抗失稳破坏验算安全系数，一般取1.15； ${N_{{\text{u}}}}$ 为钢护筒与封底层黏聚力；G封底层自重； P为封底层底部所受总孔隙水压力。

钢护筒与封底层黏聚力 ${N_{{\text{u}}}}$ 为

${N_{{\text{u}}}} = 2{{\text{π }}}{n_0}{r_0}d{\tau _{{\text{u}}}}。$

(44)

式中： ${n_0}$ 为钢护筒个数； ${r_0}$ 为钢护筒半径； ${\tau _{{\text{u}}}}$ 为钢护筒摩阻力；d为封底层厚度。

利用式（42），求得孔隙水压力表达式为

$P = \int_0^c {2{{\text{π }}}\rho gu(r)r{{\text{d}}}r} = {{\text{π }}}{c^2}d\left( {1 - {D_0}\frac{{{k_1}}}{{{k_0}}}} \right){\gamma _{{\text{w}}}}。$

(45)

式中： ${D_0}$ 为区域④水头函数的待定系数； ${\gamma _{{\text{w}}}}$ 为水的重度；c为围堰半径；k₀，k₁分别为封底层以及封底层以及土层渗透系数，对应本文解析计算模型，见图 1。钢护筒的存在减小了封底混凝土的表面积，进而影响了封底层渗流量以及所受水压力的数值，需扣除钢护筒所占面积，对渗流量公式、水压力进行修正。修正后的封底层渗水量公式为

${Q_0} = - {S_0}{k_0}{A_0} 。$

(46)

式中： ${Q_0}$ 为修正后的渗流量； ${A_0}$ 为解析解中水头函数的系数； ${S_0}$ 为扣除钢护筒后的封底层净面积， ${S_0} = {{\text{π }}}{c^2} - {n_0}{{\text{π }}}r_0^2$ 。

结合式（23），（44），（45）获得修正后的水压力公式为

${P_0} = {S_0}d\left( {1 + \frac{{{Q_0}}}{{{k_0}{S_0}}}} \right){\gamma _{{\text{w}}}}。$

(47)

式中： ${P_0}$ 为修正后的水压力公式； ${D_0}$ 为水头函数系数。封底层自重可表示为

$G = {\gamma _{{\text{g}}}}{{\text{d}}}{S_0}。$

(48)

式中： ${\gamma _{{\text{g}}}}$ 为封底层土体的重度。

联立式（43）~（47），可得考虑渗流影响下圆形围堰封底层失稳极限平衡方程为

${K_1}\left( {{\gamma _{{\text{g}}}} + \frac{{2{{\text{π }}}{n_0}r_0^2{\tau _{{\text{u}}}}}}{{{S_0}}}} \right) \geqslant \left( {1 + \frac{{{Q_0}}}{{{S_0}{k_0}}}} \right){\gamma _{{\text{w}}}}。$

(49)

3.3 工程实例分析

结合具体工程实例^[17]，利用式（49）对封底层厚度的优化设计进行探讨。

徐明高速淮河特大桥20号承台为直径26.0 m的圆形承台，基础采用18根直径2 m的钻孔桩，承台基坑开挖采用无内支撑的圆形钢板桩围堰，围堰直径为31.64 m，洪水水面到承台底高差为13.83 m，基坑开挖深度达16.9 m（封底层3.0 m）。钢板桩设计长度为27 m，其顶面控制标高为+17.000 m，桩底标高为-10.000 m，钢板桩有效入土深度9.6 m。

钢围堰埋深范围内地质情况：①软土流塑，主要由淤泥质粉质黏土和粉土组成，层厚2.6~6.0 m。②砂质黏土硬塑，密实坚硬，层厚2.5~4.0 m。③粉砂饱和，密实，局部夹粉质黏土和粉土薄层，层厚6.0~11.5 m。为简化分析，将土层概化为双层土，上层为粉砂层（夹黏土），渗透系数 ${k_1} = 6 \times {10^{ - 6}}{{\text{ m}}}/{{\text{s}}}$ ，下层为粉细砂层，渗透系数 ${k_2} = 5 \times {10^{ - 5}}{{\text{ m}}}/{{\text{s}}}$ ，具体计算参数见图 7。

由3.1节可知，静水压力大于渗流情况下的水压力，故先采用静水压力计算封底层厚度，静水压力作用下封底层厚度计算公式为

$d = \frac{{{\gamma _{{\text{w}}}}h{S_0}}}{{{K_1}[{\gamma _{{\text{g}}}}{S_0} + 2{{\text{π }}}{n_0}{r_0}{\tau _{{\text{u}}}}]}}。$

(50)

式中： ${\gamma _{{\text{w}}}}$ 取10 kN/m， ${\gamma _{{\text{g}}}}$ 取24 kN/m； $h$ 为围堰内外水头差。根据相关文献研究结果，封底层与桩基钢护筒之间的握裹力系数一般取0.15~0.2 MPa，本文计算采用0.15 MPa^[18]，即 ${\tau _{{\text{u}}}}$ =150 kN/m²，经计算不考虑渗流作用时封底层厚度需为2.6 m。

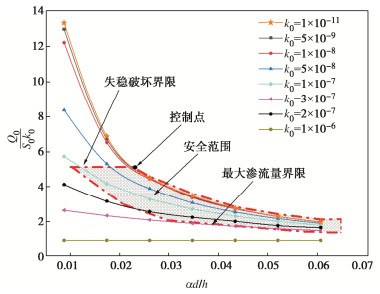
利用本文解析解计算了不同封底层渗透系数情况下封底层表面的渗流量值，以包含渗流量的无量纲参数 ${Q_0}/{S_0}{k_0}$ 与包含封底层厚度的无量纲参数 $\alpha d/h$ （其中 $\alpha = \sqrt {{k_1} \cdot {k_2}}$ ）反映渗流量与封底层厚度的变化关系，如。结果表明： ${Q_0}/{S_0}{k_0}$ 随封底层厚度（ $\alpha d/h$ ）的增加而减小，渗透系数越小，随封底层厚度的变化幅度越小，渗透系数与下部土层一致时， ${Q_0}/{S_0}{k_0}$ 的值不再发生变化；封底层厚度一定时，随着渗透系数的减小， ${Q_0}/{S_0}{k_0}$ 值会变大，变化值会随渗透系数减小而减小。经过计算，当 ${k_0} < 1 \times {10^{ - 11}}{{\text{ m/s}}}$ 后， $Q/{S_0}{k_0}$ 值会逐渐拟合为一条曲线。

图 8 封底层渗水量变化图

Figure 8. Change in water infiltration at bottom of seal

下载: 全尺寸图片幻灯片

由于 ${k_0} < 1 \times {10^{ - 11}}{{\text{ m/s}}}$ 后， ${Q_0}/{S_0}{k_0}$ 的值随封底层厚度的变化规律基本一致，故可采用 ${k_0} = 1 \times {10^{ - 11}}{{\text{ m/s}}}$ 的曲线确定失稳界限。已计算出不透水情况下（封底层渗透系数极小），封底层厚度需为2.6 m，在 ${k_0} = 1 \times {10^{ - 11}}{{\text{ m/s}}}$ 曲线上，封底层厚度2.6 m对应的 ${Q_0}/{S_0}{k_0}$ 值为5.1，以此确定失稳破坏界限。

理论上渗透系数越大封底层越不易发生失稳破坏，但封底层渗水量一般都应控制在一定范围以内，由封底层最大允许渗水量[Q_u]控制。文献[]中，基坑单位面积（1.0 m）的水平封底隔渗帷幕最大允许渗水量设计值[q]设为 ${{\text{0}}}{{\text{.25 }}}{{{\text{m}}}^3}/{{\text{d}}}$ ，考虑到围堰封底层渗透系数要求更高，[q_u]取 ${{\text{0}}}{{\text{.05 }}}{{{\text{m}}}^3}/{{\text{d}}}$ ，经换算封底层最大允许渗水量[Q_u]为0.00047 m³/s。

4. 结论

本文将圆形围堰稳态渗流场分为4个区域，用分离变量法推导出了4个区域的水头解析解，结合区域间的连续条件并利用贝塞尔函数正交性构造了非齐次线性方程组，求解方程组确定了解析解中的待定系数。基于解析解进一步推导了开挖面水力梯度及涌水量表达式，计算分析了封底层渗流水压力，结合工程实例对封底层厚度优化设计进行了探讨，获得3点结论。

（1）本文解析解为显示解析解，可求解渗流场任意一点水头，以及围堰出口水力坡度、涌水量等渗流场参数，通过对比数值计算结果以及其它研究者的计算数据，证明了本文解析解的精确性及可靠性。

（2）渗流情况下封底层所受水压力呈中心小四周大的分布形式，封底层厚度越小，该分布形式越明显；渗流情况下封底层所受水压力会随封底层渗透系数的增大而减小。

（3）在渗流量随封底层厚度的变化图给出了安全范围，可对考虑失稳破坏情况下封底层厚度的初步优化设计提供一定参考。

图 1 围堰渗流模型

Figure 1. Model for seepage around cofferdam

下载: 全尺寸图片幻灯片

图 2 涌水量计算示意图

Figure 2. Seepage quantity of unit circle

下载: 全尺寸图片幻灯片

图 3 围堰周围的水头分布

Figure 3. Distribution of water heads around cofferdam

下载: 全尺寸图片幻灯片

图 4 模型几何边界条件

Figure 4. Geometrical and boundary conditions of model

下载: 全尺寸图片幻灯片

图 5 开挖面涌水量对比结果

Figure 5. Comparison of analytical solutions, MoF and numerical model solutions by Madanayaka

下载: 全尺寸图片幻灯片

图 6 水压力分布图

Figure 6. Distribution of seepage pressure

下载: 全尺寸图片幻灯片

图 7 计算参数图

Figure 7. Computational parameters

下载: 全尺寸图片幻灯片

图 8 封底层渗水量变化图

Figure 8. Change in water infiltration at bottom of seal

下载: 全尺寸图片幻灯片

表 1 围堰渗流模型的工程参数

Table 1 Engineering parameters of seepage model for cofferdam 单位: m

b c d T₁ T₂ h₁ h₂ a

50 10 5 15 25 18 30 5

下载: 导出CSV

参考文献(18)

[1]	MADANAYAKA T A, SIVAKUGAN N. Adaptation of method of fragments to axisymmetric cofferdam seepage problem[J]. International Journal of Geomechanics, 2017, 17(9): 121-129.
[2]	MADANAYAKA T A, SIVAKUGAN N. Simple solutions for square and rectangular cofferdam seepage problems[J]. Canadian Geotechnical Journal, 2019, 56(5): 730-745. doi: 10.1139/cgj-2018-0295
[3]	BENMEBAREK N, BENSMAINE A, Critical hydraulic head loss inducing cofferdam failure embedded in horizontal sandy ground[J]. Alexandria Engineering Journal, 2015, 51(4): 173-180.
[4]	TANAKA T, TACHIMURA R, KUSUMI S, et al. Experimental findings of 3D seepage failure of soil within a cofferdam[J]. Japanese Geotechnical Society Special Publication, 2016, 45(2): 1608-1613.
[5]	薛禹群, 吴吉春. 地下水动力学[M]. 3版. 北京: 地质出版社, 2010. XUE Yuqun, WU Jichun. Groundwater Hydraulics[M]. 3rd ed. Beijing: Geological Publishing House, 2010. (in Chinese)
[6]	KAVVADAS M, GIOLAS A, PAPACHARALAMBOUS G. Drainage of supported excavations[J]. Geotechnical & Geological Engineering, 1992, 10(2): 141-157.
[7]	BANERJEE S, MULESHKOV A. Analytical solution of steady seepage into double-walled cofferdams[J]. Journal of Engineering Mechanics, 1992, 118(3): 525-539. doi: 10.1061/(ASCE)0733-9399(1992)118:3(525)
[8]	BERESLAVSKII E N. The flow of ground waters around a Zhukovskii sheet pile[J]. Journal of Applied Mathematics and Mechanics, 2011, 75(2): 210-217. doi: 10.1016/j.jappmathmech.2011.05.010
[9]	NEVEU, G. Axisymmetrical Seepage Flowthrough A Circular Sheet Pile Cofferdam[D]. Montreal: McGill Univ, 1972.
[10]	MADANAYAKA T A, SIVAKUGAN N. Validity of the method of fragments for seepage analysis in circular cofferdams[J]. Geotechnical and Geological Engineering, 2020, 38(2): 1547-1565. doi: 10.1007/s10706-019-01111-9
[11]	大卫登可夫R N, 佛兰克O L, 远泓. 漫水地区板桩基坑三向渗流研究[J]. 水利水运科技情报, 1973(增刊3): 50-68. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY1973S3006.htm DAVIDENKOFF R N, FRANKE O L, YUAN Hong. A Study on Three Dimensional Seepage of Sheet Pile Foundation Pit in Overflow Areas[J]. Hydro-Science and Engineering, 1973(S3): 50-68. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY1973S3006.htm
[12]	MADANAYAKA T A, SIVAKUGAN N. Approximate equations for the method of fragment[J]. International Journal of Geotechnical Engineering, 2016, 10(3): 297-303. doi: 10.1080/19386362.2016.1144338
[13]	李佩成. 地下水非稳定渗流解析法[M]. 北京: 科学出版社, 1990. LI Peicheng. Analytical Method for Unsteady Seepage of Groundwater[M]. Beijing: Science Press, 1990. (in Chinese)
[14]	张承宗. 数学物理方法与复数特殊函数[M]. 北京: 中国宇航出版社, 2014. ZHANG Chengzong. Anisotropic Mathematical Physics and Complex Special Functions[M]. Beijing: China Astronautic Publishing House, 2014. (in Chinese)
[15]	王竹溪, 郭敦仁. 特殊函数概论[M]. 北京: 北京大学出版社, 2000. WANG Zhuxi, GUO Dunren. Introduction to Special Function[M]. Beijing: Peking University Press, 2000. (in Chinese)
[16]	BOUCHELGHOUM F, BENMEBAREK N, Critical hydraulic head loss assessment for a circular sheet pile wall under axisymmetric seepage conditions. [J]. Studia Geotechnica et Mechanica, 2011, 3(4): 3-23.
[17]	李仁民, 刘伟, 陈晓凤. 大直径圆形钢板桩围堰施工技术[J]. 施工技术, 2013, 42(13): 33-37. https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS201313013.htm LI Renmin, LIU Wei, CHEN Xiaofeng. Construction technology of large-diameter circular steel sheet pile cofferdam[J]. Construction Technology, 2013, 42(13): 33-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS201313013.htm
[18]	曹成勇, 施成华, 彭立敏, 等. 深厚强透水地层基坑深层水平封底隔渗帷幕设计方法及其应用[J]. 中南大学学报(自然科学版), 2020, 51(4): 1012-1021. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202004016.htm CAO Chengyong, SHI Chenghua, PENG Limin, et al. Design method and application of horizontal bottom sealing curtains for deep foundation pits excavated in deep aquifers with high permeability[J]. Journal of Central South University (Science and Technology), 2020, 51(4): 1012-1021. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202004016.htm

施引文献(3)

期刊类型引用(2)

1.	倪登云，龚彪，陈洪杰，蒋加宝，魏婧怡，李艳春. 富水深厚砂层中深大基坑封底加固效果模拟分析研究. 建筑施工. 2025(01): 98-102 . 百度学术
2.	韩贇，朱浩杰，刘小刚，黄山景. 水位升降和潮汐水位作用下围堰的安全稳定性. 华侨大学学报(自然科学版). 2024(02): 219-225 . 百度学术