Model for well hydraulics of constant-head injection using a partially penetrating well considering clogging in well vicinity
-
摘要: 针对传统定水头井流模型无法反映井周含水层堵塞对含水层渗流响应影响的问题,在假设井周含水层渗透系数在堵塞作用下随时间呈指数形式衰减的基础上,建立了考虑堵塞效应的定水头非完整回灌井流模型。通过对模型进行变量代换、Laplace变换和有限余弦Fourier变换及其逆变换,推导了定解问题在Laplace空间的解,并采用Stehfest数值逆变换方法得到了实时空间内的半解析解。参数分析结果表明,较小的渐近渗透系数Kr, ∞会减小回灌过程中回灌流量和水头抬升,并降低含水层的拟稳态渗流响应,而较大的渗透系数衰减指数λ仅降低了渗透系数衰减过程中水头抬升和回灌流量,并不影响含水层达到拟稳态时的渗流状态;因Kr, ∞和λ不同引起的水头差沿径向距离先增大后减小,在井周堵塞区与主含水层交界面达到最大值;回灌堵塞使得水头抬升分布在井周堵塞区与主含水层交界面上存在明显的折点,并造成含水层水头在抬升过程中存在显著的下降阶段,上述特征可为回灌堵塞评估与预测提供参考。Abstract: To address the issue that the traditional models of well hydraulics for constant-head tests (CHTs) fail to reflect the effects of the clogging in well vicinity on groundwater flow dynamics, a semi-analytical model of the groundwater hydraulics in well vicinity is developed for CHTs using partially penetrating wells. A combination of variable substitution, Laplace transform and finite Fourier cosine transform is used to develop the solutions for the proposed model in the Laplace domain. Then, the solutions in the real-time domain are obtained using the Stehfest numerical Laplace inversion method. A parametric study of the developed solution indicates that a smaller asymptotic hydraulic conductivity Kr, ∞ leads to the smaller hydraulic head increment s and the less injection flux Q and reduces the quasi-steady flow dynamics of the recharged aquifer, while a larger permeability reduction exponent λ decreases s and Q only in the middle stage of the injection tests but has few effects on the quasi-steady flow dynamics. The hydraulic head difference due to various values of Kr, ∞ and λ first increases and then decreases with the radial distance and reaches its maximum value at the interface of the clogging region and the formation. The clogging in well vicinity results in an obvious inflection point at the outside boundary of the clogging region on the distribution curve of s and leads to an apparent decreasing stage of the history curve of s, which can offer theoretical reference for the evolution and prediction of the clogging development.
-
0. 引言
在基坑工程中,地下水回灌常被用于控制或消除基坑降水对周围环境的影响。地下水回灌可以分为定流量回灌和定水头回灌,其中定水头回灌常用于低渗透性含水层的水位抬升[1-3]。最早的定水头井流模型是由Jacob等[4]建立的。该模型描述了水平无限延伸的均质承压含水层中完整井定降深条件下的径向水流运动。在此基础上,国内外众多学者考虑含水层越流、表皮效应、非完整井、含水层类型等因素的影响,对Jacob等模型进行了改进并推导了相应的解析解或半解析解[1-3]。由于地下水回灌通常被视为地下水开采的逆过程,上述单井定降深井流模型可同样为定水头回灌条件下的含水层渗流响应分析提供参考。然而,由于相反的水流流动方向改变了井周的物理条件,不同于抽汲地下水在井周形成的渗透增高地带,回灌地下水携带的细颗粒会随着水流速度下降逐渐沉积而在井周形成一个渗透衰减地带[5]。与此同时,回灌水中溶解的气泡、回灌水与地下水或含水层介质间的化学反应以及滤管周围微生物的生长繁殖均可能进一步加剧井周含水层渗透性衰减。上述物理、生物与化学过程导致的渗透衰减使得基于恒定渗透系数的抽水井流模型不再适用于分析回灌井流问题。
为考虑回灌过程中渗透衰减效应,何满潮等[6]通过对地热水回灌的测试数据分析,建立了考虑井周物理与化学阻塞效应的渗透系数衰减模型。随后,何满潮等[5]将该服从指数衰减的渗透模型引入经典的Theis模型[7],推导了考虑渗透系数动态衰减的单井回灌公式,并分析了渗透衰减对于回灌井周渗流场的影响。基于上述单井回灌公式,闫峭等[8]利用改进遗传算法研究了考虑渗透系数衰减的水文地质参数反演问题。上述研究均只考虑了定流量回灌,并未涉及定水头回灌。对于由回灌压力控制的回灌井流问题,李炯等[9]将何满潮等[6]提出的渗透衰减方程引入至Jacob等[4]模型,并利用Weber变换得到了模型的解析解,但该模型未考虑回灌井非完整性的影响。此外,上述研究均假设整个含水层的渗透系数存在同步衰减,而现实中回灌堵塞通常仅存在于回灌井邻近的柱状包围带[5],堵塞对主含水层渗透性的影响非常轻微。
为分析定水头非完整井回灌过程中井周堵塞效应对承压含水层渗流场的影响,本文选用指数形式的渗透方程代替恒定渗透系数反映堵塞作用下的井周含水层渗透衰减行为,建立了考虑井周堵塞效应的非完整井定水头回灌井流模型。通过变量代换、Laplace变换和有限余弦Fourier变换及其逆变换,推导了井流模型在Laplace空间的解,并利用Stehfest数值逆变换方法得到了实时空间内的半解析解,并进一步分析了回灌堵塞诱发的渗透衰减对定水头非完整井回灌渗流场的影响规律。研究结果可以为定水头回灌的工程设计、参数反演、堵塞治理提供理论参考。
1. 问题的提出与求解
1.1 渗透衰减模型
由于物理、生物以及化学因素引起的堵塞在回灌井周围并不是均匀分布的,距离回灌井越近,地层堵塞越严重,渗透系数下降越显著,使得回灌堵塞影响下的井周含水层渗透系数兼有时间和空间变异性。然而,当前试验条件下准确获得径向流动过程中的堵塞时空发展规律及其导致的渗透时空变异规律是非常困难的。同时,考虑时空变异的渗透衰减方程对于井流模型的解析求解亦提出了更高的要求。为便于求解与分析,本文仅考虑渗透系数的时变效应。需要指出的是,这里的渗透系数表征的是整个井周堵塞区而非某一给定位置的水力传导性能,是对堵塞区实际渗透系数在空间上的平均唯象近似。
基于上述分析,为考虑回灌堵塞对含水层导水特性的影响,本文假设井周含水层在水平和竖直方向上的渗透系数均服从Bianchi等[10]基于室内水平砂柱试验建立的反映堵塞作用下渗透衰减问题的概括性方程。该方程具有如下形式:
$$ {K_{\text{r}}}(t) = {K_{{\text{r}},\infty }} + ({K_{{\text{r}},0}} - {K_{{\text{r}},\infty }})\exp ( - {\lambda _0} \cdot t) \;\;\text{,} $$ (1a) $$ {K_{\text{z}}}(t) = {K_{{\text{z}},\infty }} + ({K_{{\text{z}},0}} - {K_{{\text{z}},\infty }})\exp ( - {\lambda _0} \cdot t) \;\;。 $$ (1b) 式中:Kr和Kz分别为含水层水平和竖直方向上的渗透系数;“0”和“∞”分别表示渗透系数的初始与渐近值;$ {\lambda _0} $为渗透系数随时间的衰减指数。当Kr = Kz且K∞ = 0时,上述渗透衰减模型可退化至何满潮等[6]提出的渗透衰减模型。此外,为便于数学分析,本文假设含水层水平和竖向渗透系数具有相同的衰减速率,即相同的$ {\lambda _0} $,且两者之比的初始值和稳定值保持不变,即Kr, 0/Kz, 0 = Kr, ∞/Kz, ∞ =$ {\alpha ^2} $。此时,在整个渗透衰减过程中Kr(t)与Kz(t)的比值亦为定值$ {\alpha ^2} $。
1.2 数学模型
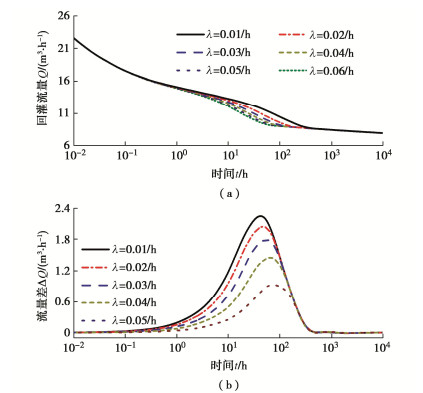
本文选用的非完整井定水头回灌模型位于图 1所示的含水层系统中。该含水层系统由一个均质等厚、侧向无限延伸的水平各向同性承压含水层及其上覆和下伏隔水层组成,是一种工程实践中常见的含水层系统,便于开展相关的野外现场测试和室内模型试验,从而有利于验证理论模型的适用性和准确性。同时,该含水层系统也被众多经典井流模型选用,如Yang等[3]建立的考虑表皮效应的两区井流模型。鉴于此,本文采用了与Yang等模型几乎完全相同的含水层假设。但不同于Yang等假定井周表皮层渗透系数随时间恒定,本文模型须考虑回灌堵塞造成的井周含水层渗透衰减效应。对于井周含水层回灌堵塞区,参考Yang等[3]对表皮层的处理方式,本文假设井周堵塞区的径向延伸rc沿深度保持不变,呈圆柱状分布,如图 1所示。在该柱状包围带内,含水层具有良好的均质性,不同位置的渗透系数受堵塞效应影响而随时间同步衰减。
基于上述假设,以回灌井轴线与含水层底板交点为原点、回灌井轴线竖直向上为z轴、含水层底板水平径向延伸为r轴建立柱坐标系。分别用式(1a)和式(1b)代替Yang等[3]模型中水平与竖直方向上的常渗透系数,则考虑堵塞效应的非完整井定水头回灌模型的控制方程可以描述为
$$ {K_{\text{r}}}(t)\left[ {\frac{{{\partial ^2}s}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial s}}{{\partial r}}} \right] + {K_{\text{z}}}(t)\frac{{{\partial ^2}s}}{{\partial {z^2}}} = \frac{S}{B}\frac{{\partial s}}{{\partial t}}\;\;。 $$ (2) 式中:s为含水层的水头抬升;r和z分别为到回灌井轴线的径向距离和到含水层底板的垂向距离;t为回灌时间;S为含水层储水系数;B为含水层厚度。
回灌开始前,井周含水层初始水头变化为零:
$$ s(r,z,t) = 0,{\text{ }}t = 0\;\;。 $$ (3) 回灌过程中,井筒内的平均压力水头恒为sw:
$$ \frac{1}{{l - d}}{\left. {\int_d^l {s(r,z,t)} {\text{d}}z} \right|_{r = {r_{\text{w}}}}} = {s_{\text{w}}}{\text{ (}}d \leqslant z \leqslant l) \;\;。 $$ (4) 式中:rw为回灌井半径;l和d分别为回灌井过滤器顶端与底端的竖向坐标。
在回灌井内,假设定水头作用下回灌流量Q(t)沿滤管均匀分布,则有
$$ {\left. { - 2{\text{π }}r(l - d){K_{\text{r}}}(t){{\partial s(r,z,t)} \mathord{\left/ {\vphantom {{\partial s(r,z,t)} {\partial r}}} \right. } {\partial r}}} \right|_{r = {r_{\text{w}}}}}{\text{ = }}Q(t){\text{ (}}d \leqslant z \leqslant l) \;\;。 $$ (5) 回灌过程中,沿井壁套筒流量为零,含水层与下伏和上覆弱透水层的交界面完全隔水,则有
$$ {\left. {{{\partial s(r,z,t)} \mathord{\left/ {\vphantom {{\partial s(r,z,t)} {\partial r}}} \right. } {\partial r}}} \right|_{r = {r_{\text{w}}}}} = {\text{0 (}}z \leqslant d,{\text{ }}z \geqslant l) \;\;\text{,} $$ (6) $$ {{\partial s(r,z,t)} \mathord{\left/ {\vphantom {{\partial s(r,z,t)} {\partial z}}} \right. } {\partial z}} = 0\;\;\;{\text{ (}}z = 0)\;\;\text{,} $$ (7) $$ {{\partial s(r,z,t)} \mathord{\left/ {\vphantom {{\partial s(r,z,t)} {\partial z}}} \right. } {\partial z}} = 0\;\;\;{\text{ (}}z = B)\;\;。 $$ (8) 回灌过程中,井周堵塞区与主含水层的交界面上的水头抬升如下式所示:
$$ s\left(r_{\mathrm{c}}, z, t\right)=s_{\mathrm{c}}(z, t) \quad(0 \leqslant z \leqslant B) \;\;。 $$ (9) 式中,sc(z, t)为回灌流量等于Q(t)且不考虑井周堵塞效应时求得的r = rc处的水头抬升,其表达式与Feng等[1]推导的变流量条件下承压含水层中水头变化公式相同。式(9)实际上忽略了井周堵塞对主含水层的渗流场的影响。根据Yeh等[11]对考虑表皮效应的两区井流模型的分析结果可知,试井周围的低渗透区域仅会在试验初期对主含水层渗流场有轻微影响。随着井周渗流场在很短时间内达到拟稳态,该影响仅会在试验初期带来非常微小的误差,是可以接受的。
1.3 问题的求解
式(2)~(9)构成了考虑井周堵塞效应的非完整井定水头回灌井流模型的定解问题。为便于求解,首先对定解问题作如下变量代换:
$$ r^{\prime} = {r \mathord{\left/ {\vphantom {r \alpha }} \right. } \alpha } \;\;\text{,} $$ (10) $$ t^{\prime} = {K_{{\text{z}},\infty }}t/{K_{{\text{z}},0}} + ({K_{{\text{z}},0}} - {K_{{\text{z}},\infty }})(1 - {{\text{e}}^{ - {\lambda _0}t}})/({\lambda _0}{K_{{\text{z}},0}}) \;\;\text{,} $$ (11) 式中,$ \alpha = \sqrt {{{{K_{{\text{r,0}}}}} \mathord{\left/ {\vphantom {{{K_{{\text{r,0}}}}} {{K_{{\text{z,0}}}}}}} \right. } {{K_{{\text{z,0}}}}}}} = \sqrt {{{{K_{{\text{r,}}\infty }}} \mathord{\left/ {\vphantom {{{K_{{\text{r,}}\infty }}} {{K_{{\text{z,}}\infty }}}}} \right. } {{K_{{\text{z,}}\infty }}}}} $。经过坐标变换之后,含水层的水头抬升s(r, z, t)用s'(r', z, t')表示,则定解问题转换为
$$ \frac{{{\partial ^2}s^{\prime}}}{{\partial {{r^{\prime}}^2}}} + \frac{1}{{r^{\prime}}}\frac{{\partial s^{\prime}}}{{\partial r^{\prime}}} + \frac{{{\partial ^2}s^{\prime}}}{{\partial {z^2}}} = \frac{S}{{B{K_{{\text{z}},0}}}}\frac{{\partial s^{\prime}}}{{\partial t^{\prime}}} \;\;\text{,} $$ (12) $$ s^{\prime}\left( {r^{\prime},z,t^{\prime}} \right) = 0,{\text{ }}t^{\prime} = 0\;\;\text{,} $$ (13) $$ \frac{1}{{l - d}}{\left. {\int_d^l {s^{\prime}(r^{\prime},z,t^{\prime})} {\text{d}}z} \right|_{r^{\prime} = {{r}_{\text{w}}^{\prime}}}} = {s_{\text{w}}}\;\;\;{\text{ (}}d \leqslant z \leqslant l) \;\;\text{,} $$ (14) $$ {\left. {\frac{{\partial s^{\prime}(r^{\prime},z,t^{\prime})}}{{\partial r^{\prime}}}} \right|_{r^{\prime} = {{r}_{\text{w}}^{\prime}}}}{\text{ = }} - \frac{{{{Q^{\prime}}_1}(t^{\prime})}}{{2{\text{π }}{{r}_{\text{w}}^{\prime}}(l - d){K_{{\text{r,0}}}}}}\;\;\;{\text{ (}}d \leqslant z \leqslant l) \;\;\text{,} $$ (15) $$ {\left. {{{\partial s^{\prime}(r^{\prime},z,t^{\prime})} \mathord{\left/ {\vphantom {{\partial s^{\prime}(r^{\prime},z,t^{\prime})} {\partial r^{\prime}}}} \right. } {\partial r^{\prime}}}} \right|_{r^{\prime} = {{r}_{\text{w}}^{\prime}}}} = 0\;\;\;{\text{ (}}z \leqslant d,{\text{ }}z \geqslant l) \;\;\text{,} $$ (16) $$ {{\partial s^{\prime}(r^{\prime},z,t^{\prime})} \mathord{\left/ {\vphantom {{\partial s^{\prime}(r^{\prime},z,t^{\prime})} {\partial z}}} \right. } {\partial z}} = 0\;\;\;{\text{ (}}z = 0)\;\;\text{,} $$ (17) $$ {{\partial s^{\prime}{\text{(}}r^{\prime},z,t^{\prime}{\text{)}}} \mathord{\left/ {\vphantom {{\partial s^{\prime}{\text{(}}r^{\prime},z,t^{\prime}{\text{)}}} {\partial z}}} \right. } {\partial z}} = 0\;\;\;{\text{ (}}z = B)\;\;\text{,} $$ (18) $$ s^{\prime}({r^{\prime}_{\text{c}}},z,t^{\prime}){\text{ = }}{s^{\prime}_{\text{c}}}(z,t^{\prime})\;\;\;{\text{ (}}0 \leqslant z \leqslant B) \;\;。 $$ (19) 其中,式(15)中$ {Q^{\prime}_1}\left( {t^{\prime}} \right){\text{ = }}{{Q^{\prime}\left( {t^{\prime}} \right){K_{{\text{r,0}}}}} \mathord{\left/ {\vphantom {{Q^{\prime}\left( {t^{\prime}} \right){K_{{\text{r,0}}}}} {{{K^{\prime}}_{\text{r}}}\left( {t^{\prime}} \right)}}} \right. } {{{K^{\prime}}_{\text{r}}}\left( {t^{\prime}} \right)}} $,Q'(t')和Kr'(t')以及式(19)中的$ {s^{\prime}_{\text{c}}}(z,t^{\prime}) $分别为回灌流量Q(t)、渗透系数方程Kr(t)以及堵塞区外部水头抬升$ {s_{\text{c}}}(z,t) $作关于时间的变量代换之后得到的表达式。由于根据式(11)获得t'关于t的表达式十分困难,使得上述表达式的具体形式同样难以确定。根据$ {s^{\prime}_{\text{c}}}(z,t^{\prime}) = {s_{\text{c}}}(z,t(t^{\prime})) $,$ {s^{\prime}_{\text{c}}}(z,t^{\prime}) $可表示为$ {s_{\text{c}}}(z,t^{\prime}) $与$ \Delta {s_{\text{c}}}(z,t^{\prime}) $之和,其中$ \Delta {s_{\text{c}}}(z,t^{\prime}) $的表达式通过非线性拟合求得。考虑到后续求解需要对$ \Delta {s_{\text{c}}}(z,t^{\prime}) $分别进行关于z和t'的积分变换,因此$ \Delta {s_{\text{c}}}(z,t^{\prime}) $的拟合公式宜采用如下可分离变量的形式:
$$ \Delta {s_{\text{c}}}(z,t^{\prime}) = \Delta {s_{\text{c}}}(z) \cdot \Delta {s_{\text{c}}}(t^{\prime}) \;\;。 $$ (20a) 同时,根据Laplace变换和有限Fourier变换的定义,当原函数为指数函数时,可以直接求得积分变换后的象函数。因此,$ \Delta {s_{\text{c}}}(z) $和$ \Delta {s_{\text{c}}}(z) $宜采用如下形式的分段指数函数进行拟合:
$$ \Delta {s_{\text{c}}}(t^{\prime}) = \left[ {U(t^{\prime} - {{t^{\prime}}_{i + 1}}) - U(t^{\prime} - {{t^{\prime}}_i})} \right]\left[ {{A_i} + {A_{i + 1}}\exp ({\alpha _i}t^{\prime})} \right] \;\;\text{,} $$ (20b) $$ \Delta {s_{\text{c}}}(z) = \left[ {U(z - {z_{j + 1}}) - U(z - {z_j})} \right]\left[ {{C_j} + {C_{j + 1}}\exp ({\varepsilon _j}z)} \right] \;\;。 $$ (20c) 式中:Ai,$ {\alpha _i} $,Cj及εj为根据$ {s_{\text{c}}}\left[ {z,t(t^{\prime})} \right] $与$ {s_{\text{c}}}(z,t^{\prime}) $的差值序列确定的拟合参数;U(·)为Heaviside跃阶函数,当t < $ {t_i} $时,U$ (t - {t_i}) $= 0,当t ≥$ {t_i} $时,U$ (t - {t_i}) $=1,$ {t^{\prime}_i} $和$ {z_j} $为分段点。
对定解问题作关于时间$t^{\prime}$的Laplace变换和关于z的有限Fourier余弦变换可得
$$ \frac{\partial^2 \hat{\bar{s}^{\prime}}}{\partial r^{\prime 2}}+\frac{1}{r^{\prime}} \frac{\partial \hat{\bar{s}^{\prime}}}{\partial r^{\prime}}-\xi(n, p)^2 \hat{\bar{s}^{\prime}}=0\;\;\;, $$ (21) $$ \frac{1}{{l - d}}\int_d^l {\bar s^{\prime}({{r}_{\text{w}}^{\prime}},z,p)} {\text{d}}z = \frac{{{s_{\text{w}}}}}{p}{\text{ (}}d \leqslant z \leqslant l)\;\;\text{,} $$ (22) $$ \left.K_{\mathrm{r}, 0} \frac{\partial \hat{\bar{s}^{\prime}}\left(r^{\prime}, n, p\right)}{\partial r^{\prime}}\right|_{r^{\prime}=r_{\mathrm{w}}^{\prime}}=\frac{-\bar{Q}_1^{\prime}(p)}{2 \pi r_{\mathrm{w}}^{\prime}(l-d)} \cdot A(n)\;\;\text{,} $$ (23) $$ \hat{\bar{s}^{\prime}}({r^{\prime}_{\text{c}}},n,p){\text{ = }}{\hat{\bar{s}^{\prime}}_{\text{c}}}(n,p) + \Delta {\hat{\bar{s}^{\prime}}_{\text{c}}}(n,p) \;\;。 $$ (24) 式中:$\hat{\bar{s}^{\prime}}(r^{\prime},n,p)$和$ \Delta {\hat{\bar{s}^{\prime}}_{\text{c}}}(n,p) $分别为水头抬升$s(r^{\prime},n,p)$和水头差$ \Delta {s_{\text{c}}}(n,p) $在Laplace-Fourier空间的表达式,符号“-”和“^”分别表示Laplace和Hankel空间的项,p和n分别为Laplace变量和Fourier变量,$ \xi {({r}^{\prime },n,p)}^{2}={w}_{n}^{2}+Sp/(B{K}_{\text{z},0}),A(n)=[\mathrm{sin}({w}_{n}l)- $ $\sin ({w_n}d)]/{w_n}$,$ {w_n} = n{\text{π /}}B $。式(21)为零阶修正Bessel方程,通解为
$$ \begin{array}{l} \hat{\bar{s}}(r^{\prime},n,p) = {C_1}(n,p){{\text{I}}_0}\left[ {{\xi _0}(n,p)r^{\prime}} \right] + {C_2}(n,p){{\text{K}}_0} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{\xi _0}(n,p)r^{\prime}} \right] \;\;。 \end{array} $$ (25a) 式中:待定系数C1(n, p)和C2(n, p)根据边界条件式(23)和(24)确定表达式如下所示:
$$ {C}_{1}(n,p)=\frac{\widehat{\overline{{s}}^{\prime}}({{r}}_{\text{c}}^{\prime },n,p){\text{K}}_{1}\left[{\xi }_{0}(n,p){{r}}_{\text{w}}^{\prime }\right]-\frac{{\overline{{Q}}}_{1}^{\prime}(p)A(n){\text{K}}_{0}\left[{\xi }_{0}(n,p){{r}}_{\text{c}}^{\prime }\right]}{2\text{π}{{r}}_{\text{w}}^{\prime }(l-d){K}_{\text{r,0}}{\xi }_{0}(n,p)}}{{\text{I}}_{\text{1}}\left[{\xi }_{0}(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{K}}_{0}\left[{\xi }_{0}(n,p){{r}}_{\text{c}}^{\prime }\right]+{\text{K}}_{1}\left[{\xi }_{0}(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{I}}_{0}\left[{\xi }_{0}(n,p){{r}^{\prime }}_{}\right]}\text{,} $$ (25b) $$ {C}_{2}(n,p)=\frac{\widehat{\overline{{s}}^{\prime}}({{r}}_{\text{c}}^{\prime },n,p){\text{I}}_{1}\left[{\xi }_{0}(n,p){{r}}_{\text{w}}^{\prime }\right]+\frac{{\overline{{Q}}}_{1}^{\prime}(p)A(n){\text{I}}_{0}\left[{\xi }_{0}(n,p){{r}}_{\text{c}}^{\prime }\right]}{2\text{π}{{r}}_{\text{w}}^{\prime }(l-d){K}_{\text{r,0}}{\xi }_{0}(n,p)}}{{\text{I}}_{1}\left[{\xi }_{0}(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{K}}_{0}\left[{\xi }_{0}(n,p){{r}}_{\text{c}}^{\prime }\right]+{\text{K}}_{1}\left[{\xi }_{0}(n,p){{r}}_{\text{w}}^{\prime }\right]{I}_{0}\left[{\xi }_{0}(n,p){{r}}_{\text{c}}^{\prime }\right]}。 $$ (25c) 式中:Ij(·) (j = 0, 1)和Kj(·) (j = 0, 1)分别为第一类和第二类j阶虚宗量Bessel函数。对式(25)作有限Fourier余弦逆变换,则定解问题在Laplace空间的解可写作
$$ \bar s^{\prime}(r,z,p) = \frac{1}{B}\hat{\bar{s}^{\prime}}(r,0,p) + \frac{2}{B}\sum\limits_{n = 1}^\infty {\hat{\bar{s}^{\prime}}(r,n,p)} \cdot \cos ({w_n}z)\;\;。 $$ (26) 式中,${\bar Q^{\prime}_1}(p)$的表达式仍然未知,可通过将式(25)和式(26)代入边界条件式(22)确定其表达式。需要注意的是,在计算${\bar Q^{\prime}_1}(p)$时还需首先确定受堵塞区外部边界的水头抬升$ {s_{\text{c}}}(z,t) $,$ {s_{\text{c}}}(z,t) $又取决于通过过滤器的回灌流量Q(t),而Q(t)的表达式仍然未知。为此,可以首先指定Q(t)一个初始值并计算该初始值条件下的$ {s_{\text{c}}}(z,t) $,进一步根据式(26)和${\bar Q^{\prime}_1}(p)$的表达式对Q(t)进行更新,不断循环迭代即可最终确定Q(t)的近似表达式。在迭代过程中,Q(t)可用下式近似:
$$ Q(t){\text{ = }}{Q_\infty }(t) + \left[ {{Q_0}(t) - {Q_\infty }(t)} \right] \cdot \sum {\left[ {{B_i}\exp ( - {\lambda _i}t)} \right]} 。 $$ (27) 式中,Q0(t)和Q∞(t)分别为井周含水层渗透系数为Kr, 0和Kr, ∞时的回灌流量,其表达式与Yang等[3]推导的承压含水层中非完整定降深两区模型的抽水流量解相同,Bi和$ {\lambda _i} $为待定拟合参数,式(27)在i = 1且Bi = 1,$ {\lambda _1} $ =$ {\lambda _0} $时的计算结果可作为计算Q(t)的迭代初始值。
1.4 回灌初期与后期的近似解
在回灌伊始堵塞效应尚不明显,井周含水层与主含水层的导水特性无明显差异。此时,描述定水头回灌条件下井周含水层渗流场的定解问题与同等条件下主含水层渗流场的定解问题完全相同。将定解问题(2)~(9)中的Kr(t)和Kz(t)分别用Kr, 0和Kz, 0替换,则式(11)可以简化为$t^{\prime} = t$。同时,令rc → ∞,无穷远处的水头抬升可以忽略不计,即sc(z, t) = 0。保持其他条件不变,得到新的定解问题。重复前述变量代换以及积分变换过程,得到新定解问题在Laplace空间的解为
$$ \begin{array}{l} \bar s(r^{\prime},z,p) = \frac{1}{B}\frac{{\bar q^{\prime}(p)A(0){{\text{K}}_0}\left[ {{\xi _0}(0,p)r^{\prime}} \right]}}{{{\xi _0}(0,p){K_{{\text{r,0}}}}{{\text{K}}_1}\left[ {{\xi _0}(0,p){{r}_{\text{w}}^{\prime}}} \right]}} + \\ \;\;\;\;\;\;\;\;\;\;\frac{2}{B}\sum\limits_{n = 1}^\infty {\frac{{\bar q^{\prime}(p){{\text{K}}_0}\left[ {{\xi _0}(n,p)r^{\prime}} \right]A(n)}}{{{\xi _0}(n,p){K_{{\text{r,0}}}}{{\text{K}}_1}\left[ {{\xi _0}(n,p){{r}_{\text{w}}^{\prime}}} \right]}}} \cos ({w_n}z) \;\;。 \end{array} $$ (28a) 式中,$ \bar q^{\prime}(p) = {{\bar Q^{\prime}(p)} \mathord{\left/ {\vphantom {{\bar Q^{\prime}(p)} {\left[ {2{\text{π }}{{r}_{\text{w}}^{\prime}}(l - d)} \right]}}} \right. } {\left[ {2{\text{π }}{{r}_{\text{w}}^{\prime}}(l - d)} \right]}} $,可根据边界条件式(22)确定,其表达式为
$$\begin{aligned} \bar{q}(p)= & \frac{s_{\mathrm{w}}}{p}\left\{\frac{1}{B} \frac{\mathrm{K}_0\left[\xi_0(0, p) r_{\mathrm{w}}^{\prime}\right]}{\xi_0(0, p) K_{\mathrm{r}, 0} \mathrm{~K}_1\left[\xi_0(0, p) r_{\mathrm{w}}^{\prime}\right]}+\right. \\ & \left.\frac{2}{B(l-d)} \sum\limits_{n=1}^{\infty} \frac{\mathrm{K}_0\left[\xi_0(n, p) r_{\mathrm{w}}^{\prime}\right][A(n)]^2}{\xi_0(n, p) K_{\mathrm{r}, 0} \mathrm{K}_1\left[\xi_0(n, p) r_{\mathrm{w}}^{\prime}\right]}\right\}^{-1}\;\;。 \end{aligned} $$ (28b) 式(28)即为非完整井定水头回灌初期水头抬升在Laplace空间的解,也是同等回灌条件下不考虑堵塞效应的承压含水层水头抬升在Laplace空间的解,且与Feng等[1]推导的变流量条件下承压含水层中水头降深公式相同。特殊地,该解在$ r^{\prime}{\text{ = }}{r^{\prime}_{\text{c}}} $处的表达式即为式(9)右端项$ {s^{\prime}_{\text{c}}}(z,t^{\prime}) $在Laplace空间的表达式。
当回灌试验进行足够长时间,井周堵塞影响下的含水层导水特性早已稳定。井周含水层水平与竖向渗透系数分别等于Kr, ∞和Kz, ∞。将式(2)~(9)中的Kr(t)和Kz(t)分别用Kr, ∞和Kz, ∞替换,得到新的定解问题。根据式(10)进行关于r的坐标变换并重复前述Laplace变换和Fourier变换,得到新定解问题在Laplace空间的解,其待定系数C1(n, p)和C2(n, p)表示如下:
$$ {C}_{1}(n,p)=\frac{\widehat{\overline{{s}}^{\prime}}({{r}}_{\text{c}}^{\prime },n,p){\text{K}}_{1}\left[{\xi }_{\infty }(n,p){{r}}_{\text{w}}^{\prime }\right]-\frac{\overline{{Q}}^{\prime}(p)A(n){\text{K}}_{0}\left[{\xi }_{\infty }(n,p){{r}}_{\text{c}}^{\prime }\right]}{2\text{π}{{r}}_{\text{w}}^{\prime }(l-d){K}_{\text{r,}\infty }{\xi }_{\infty }(n,p)}}{{\text{I}}_{1}\left[{\xi }_{\infty }(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{K}}_{0}\left[{\xi }_{\infty }(n,p){{r}}_{\text{c}}^{\prime }\right]+{\text{K}}_{1}\left[{\xi }_{\infty }(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{I}}_{0}\left[{\xi }_{\infty }(n,p){{r}}_{\text{c}}^{\prime }\right]}\text{,} $$ (29a) $$ {C}_{2}(n,p)=\frac{\widehat{\overline{{s}}^{\prime}}({{r}}_{\text{c}}^{\prime },n,p){\text{I}}_{1}\left[{\xi }_{\infty }(n,p){{r}}_{\text{w}}^{\prime }\right]+\frac{\overline{{Q}}^{\prime}(p)A\text{(}n{\text{)I}}_{0}\left[{\xi }_{\infty }(n,p){{r}}_{\text{c}}^{\prime }\right]}{2\text{π}{{r}}_{\text{w}}^{\prime }(l-d){K}_{\text{r,}\infty }{\xi }_{\infty }(n,p)}}{{\text{I}}_{1}\left[{\xi }_{\infty }(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{K}}_{0}\left[{\xi }_{\infty }(n,p){{r}}_{\text{c}}^{\prime }\right]+{\text{K}}_{1}\left[{\xi }_{\infty }(n,p){{r}}_{\text{w}}^{\prime }\right]{\text{I}}_{0}\left[{\xi }_{\infty }(n,p){{r}}_{\text{c}}^{\prime }\right]}。 $$ (29b) 式(25a),(26),(29a),(29b)即为非完整井定水头回灌后期水头抬升在Laplace空间的解,其中$\hat{\bar{s}^{\prime}}({r^{\prime}_{\text{c}}},n,p) $的表达式与式(28a),(28b)相同,${\xi _\infty }{(n,p)^2} = w_n^2 + $$Sp/(B{K_{{\text{z}},\infty }})$。此时,$\hat{\bar{s}^{\prime}}({r^{\prime}_{\text{c}}},n,p) $表达式中的$\bar Q^{\prime}(p)$仍然未知,可联立式(25a)~(25c),(26),(28a),(28b),(29a),(29b)确定其表达式。
由于上述Laplace空间的解形式复杂,无法直接利用解析方法求得其在实时空间的表达式。本文在对比多种Laplace变换数值反演方法后,选用兼具计算效率和精度的Stehfest[12]数值反演方法计算实时空间的水头抬升。需要指出的是,Stehfest算法中求和级数的项数N对反演结果具有显著影响,试算结果表明,当8≤N≤16时不同N值对应的反演结果差别不大,因此本文在进行Laplace变换的数值反演假设N = 16。
2. 结果验证与分析
目前由于缺少相关测试数据,本节首先通过数值计算方法对本文推导的半解析解进行对比验证,随后重点分析非完整井定水头回灌过程中堵塞诱发的渗透衰减对含水层渗流响应的影响规律。本节用于的验证和分析的非完整井定水头回灌井流模型如图 1所示。如无特殊声明,本节在进行模型计算时选取的试井参数和含水层参数分别如表 1,2所示。
表 1 井身结构参数Table 1. Parameters of well structure单位: m 试井类型 回灌压力 井径 滤管长度 滤管顶端高度 滤管底端高度 回灌井 200 0.1 10 15 5 表 2 含水层水文地质参数Table 2. Hydrological parameters of recharged aquifer堵塞区厚度/m 初始渗透系数/(m·h-1) 渐近渗透系数/(m·h-1) 渗透衰减速率/h-1 含水层厚度/m 储水系数 水平 竖向 水平 竖向 1.0 0.06 0.006 0.03 0.003 0.05 20 0.004 2.1 解的验证
当l = B和d = 0时,本文建立的定解问题退化为完整井定水头回灌井流模型。此时,含水层中的渗流为径向一维流动,回灌引起的水头抬升与深度无关。这时如果对Laplace域内堵塞区外部水头抬升$ \bar s^{\prime}({r^{\prime}_{\text{c}}},p) $作有限Fourier余弦变化,则可得到
$$ \hat{\bar{s}^{\prime}}\left(r_{\mathrm{c}}^{\prime}, n, p\right)=\left\{\begin{array}{ll} B \cdot \bar{s}^{\prime}\left(r_{\mathrm{c}}^{\prime}, p\right) & (n=0) \\ 0 & (n \neq 0) \end{array}\right. \;\;。 $$ (30) 此外,将l = B,d = 0代入A(n)化简得到
$$ A(n)=\left\{\begin{array}{ll} B & n=0 \\ 0 & n \neq 0 \end{array}\right. \;\;。 $$ (31) 将式(30),(31)代入式(25),(26)即得到完整井定水头回灌井流模型在Laplace空间的半解析解。此外,完整井定水头回灌井流模型还可通过MATLAB的偏微分方程求解函数pdepe进行数值求解。该函数可以求解如下形式的偏微分定解问题:
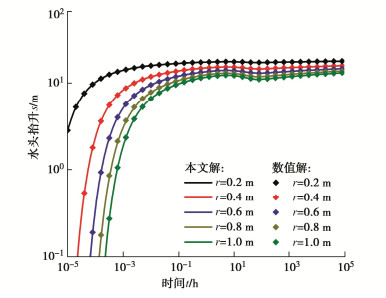
$$ c\left(x,t,u,\frac{\partial u}{\partial x}\right)\frac{\partial u}{\partial t}=\frac{1}{x}\frac{\partial }{\partial x}\left(xf\left(x,t,u,\frac{\partial u}{\partial x}\right)\right)+s\left(x,t,u,\frac{\partial u}{\partial x}\right)\text{,} $$ (32a) $$ u(x,0) = {u_0}(x) \;\;\text{,} $$ (32b) $$ p(x,t,u) + q(x,t)f(x,t,u,{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. } {\partial x}}) = 0 \;\;。 $$ (32c) 其中,式(32a)~(32c)分别为定解问题的控制方程、初值条件和边值条件,x和t分别为空间变量和时间变量,c(x, t, u, ∂u/∂t)为控制方程非定常项的系数矩阵,f(x, t, u, ∂u/∂t)和s(x, t, u, ∂u/∂t)分别为控制方程的流项和源项。将完整井定水头回灌井流模型按照式(32a)~(34c)进行改写,并编写MATLAB计算程序,得到定解问题的数值解。图 2展示了不同位置的水头抬升的半解析计算值与数值计算值的对比结果。对比结果表明,利用Stehfest算法反演得到的实时空间的解在N = 16时与相应数值解符合良好,证明本文推导半解析解的准确性以及Stehfest算法在解决考虑变渗透系数的定水头非稳定流问题的适用性。
2.2 回灌堵塞程度的影响
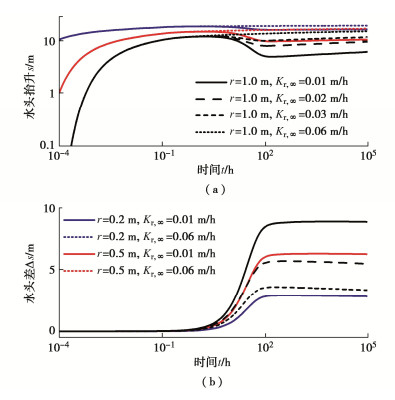
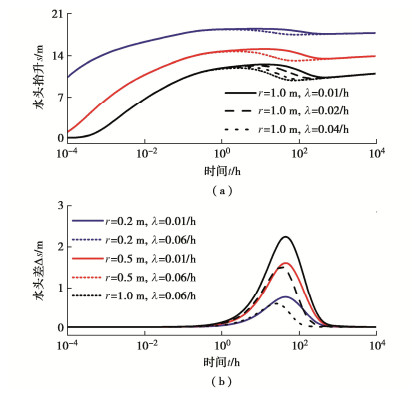
图 3所示为不同堵塞程度,即不同Kr, ∞值,对井周堵塞区内不同位置(z = 10 m,r = 0.2,0.5,1.0 m)处水头抬升的影响,其中图 3(a)为水头抬升s时程曲线,图 3(b)为考虑渗透衰减(Kr, ∞ < 0.06 m/h)与不考虑渗透衰减(Kr, ∞ = 0.06 m/h)情形下的水头差Δs时程曲线。在回灌初期,堵塞效应尚不明显,任一给定位置处不同Kr, ∞值下的s随时间以相同速度逐渐增大。在该阶段不同位置处考虑堵塞效应与否的水头差Δs基本为零。随着回灌的进行,Kr, ∞ = 0.06 m/h时的s继续随时间逐渐增大,而堵塞效应下Kr, ∞ < 0.06 m/h时的s则呈现一定下降趋势,且Kr, ∞越小,r越大,下降趋势越显著,Δs越大。至回灌后期,堵塞引起的渗透衰减趋于稳定,此时不同Kr, ∞下的s均随时间缓慢增大,Δs在达到峰值后基本保持不变或轻微下降。
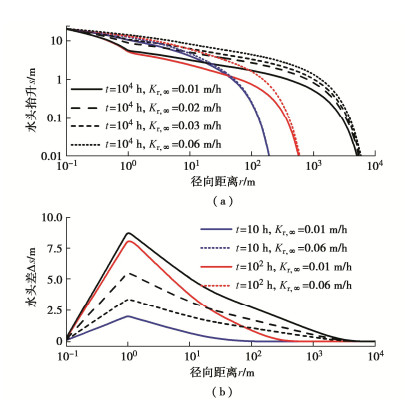
图 4所示为不同Kr, ∞值对含水层水头抬升分布的影响,其中图 4(a)为不同时刻z = 10 m深度处的水头抬升s的径向分布曲线。从图 4中可以看出,任一给定时刻t的水头抬升随径向距离r逐渐减小,且Kr, ∞越小,s下降趋势越显著,s的大小及分布范围也越小。同时,水头抬升在沿径向距离下降的过程中,在堵塞区域与主含水层交界面处存在明显的转折,Kr, ∞越小,t越大,该转折越明显。对考虑渗透衰减与否两种情形下所得水头抬升分布曲线作差,计算结果如图 4(b)所示。可以发现,水头差分布沿径向距离先迅速增大,在井周含水层与主含水层交界面达到峰值,且Kr, ∞越小,t越大,水头差峰值越大,之后随着r的增大逐渐下降至零。
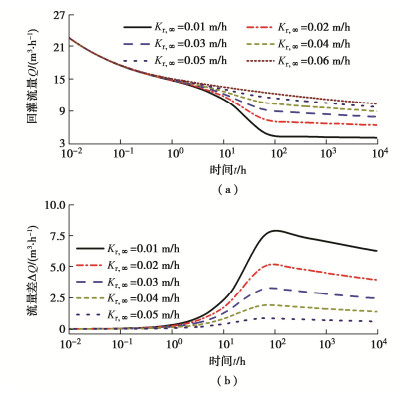
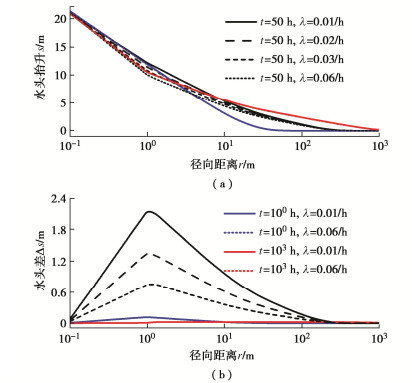
图 5所示为不同Kr, ∞对定水头条件下试验井回灌流量的影响,其中图 5(a)为回灌流量Q时程曲线,图 5(b)为考虑渗透衰减与否所得回灌流量差$ \Delta Q $时程曲线。从图 5中可以看出,堵塞诱发的渗透衰减效应显著降低了回灌流量。在回灌初期,渗透衰减效应尚不明显,不同Kr, ∞下回灌流量相差非常微小;随着渗透衰减效应的逐渐显现,Kr, ∞越小,回灌流量衰减越迅速,且考虑渗透衰减与否引起的流量差随着时间增加明显;当回灌时间足够长,渗透系数不再继续衰减,含水层中的渗流趋于拟稳态,此时不同Kr, ∞下的Q随着时间非常缓慢地下降,而$ \Delta Q $也在非常缓慢地下降。
2.3 回灌堵塞速率的影响
图 6所示为不同堵塞速率,即不同$ \lambda $值,对z = 10 m深度处井周堵塞区内含水层水头抬升的影响,其中图 6(a)为不同径向距离(r = 0.2,0.5,1.0 m)处水头抬升s时程曲线。从图 6中可以看出,任一给定位置处的s在发展过程均存在显著的下降阶段,且$ \lambda $越大,r越大,下降阶段发生越早,下降程度越显著。在回灌初期和后期,不同的$ \lambda $值对含水层水头抬升几无影响,而在回灌中期,较大的$ \lambda $值可降低水头抬升。将$ \lambda $ ≠ 0.06/h时与$ \lambda $ = 0.06/h时的s作差,计算结果如图 6(b)所示。可以发现,相对于$ \lambda $= 0.06/h时的水头抬升,越小的$ \lambda $引起的水头差Δs随时间增加越迅速、所能达到峰值越大、达到峰值所需时间越长。同时,Δs峰值大小和达到峰值所需的时间分别与r成正比和反比关系。此后,随着不同$ \lambda $下的渗透系数趋于相同的Kr, ∞,由于$ \lambda $不同引起的Δs随时间逐渐衰减至零。
图 7所示为井周含水层不同$ \lambda $值对不同时刻含水层水头抬升s分布的影响,其中图 7(a)为s的径向分布曲线,图 7(b)为因$ \lambda $不同而引起的水头抬升差Δs的径向分布曲线。从图中可以看出,任一给定时刻t的水头抬升随径向距离r逐渐减小。在回灌初期(t = 10 h)和后期(t = 1000 h),不同$ \lambda $下的s分布曲线接近重合在一起,此时的Δs分布几乎等于零。而在回灌中期(t = 50 h),$ \lambda $越小,任意r处的s越大,相应的s分布范围也越大。此时,$ \lambda $不同引起的Δs随r先增大并在井周含水层与主含水层交界面达到最大值,且$ \lambda $越小,Δs随r增速越大、所能达到的峰值越大。此后,随着r继续增大,Δs开始缓慢下降并逐渐减少至零。
图 8所示为不同$ \lambda $对定水头条件下试验井回灌流量的影响,其中图 8(a)为不同$ \lambda $情形下的回灌流量时程曲线。从图中可以看出,$ \lambda $的大小对于试验初期和后期的回灌量几乎没有影响,但在试验中期,较大的$ \lambda $可一定程度上降低回灌流量。将$ \lambda $ ≠ 0.06/h时与$ \lambda $ = 0.06/h的回灌流量时程曲线作差,计算结果如图 8(b)所示。因$ \lambda $不同而引起的回灌流量差首先随着时间增大,$ \lambda $越小,流量差的增加速度越快,流量差幅值越大,达到峰值所需的时间越短。此后,随着试验的进行,不同$ \lambda $计算得到的流量差逐渐减小为零。
3. 分析与讨论
本文的参数分析表明,堵塞程度同时改变了含水层水头抬升速度以及含水层的最终渗流状态,而堵塞速率则主要改变了含水层的渗流响应速度,并不影响含水层最初和最终的渗流状态。当井周含水层发生堵塞时,含水层渗透性下降增加了回灌水从试井流入含水层的难度,导致回灌流量的下降,进而引起整个含水层水头抬升不同程度的降低。同时,由于井筒定水头边界的约束作用,这种堵塞引起的水头抬升下降在井筒附近非常微小。随着远离井筒,水头抬升下降逐渐增大并在堵塞区与主含水层交界面达到最大值。此后,随着径向距离和过水断面的增大,井周堵塞导致的水头差逐渐减小并最终降为零。
上文的参数分析同时还表明,当考虑堵塞引起的渗透系数衰减时,含水层中水头抬升呈现先快速上升,继而明显下降,随后又继续缓慢上升的发展过程。这一现象与Wen等[13]报道的抽水流量呈指数形式衰减时引起的水头变化过程非常类似。结合Wen等[13]的研究,可以推断这种水头抬升过程中的下降趋势是由于渗透系数衰减导致恒定压力下回灌流量下降引起的。当堵塞越严重、回灌流量衰减越显著时,这种水头抬升的下降趋势越明显。由于该特征与渗透性恒定含水层中进行定水头回灌引起的承压水头持续抬升存在显著差异,这一特征可以作为判别井周含水层是否发生堵塞以及堵塞程度的判断标准。
除了水头抬升过程中出现的下降现象,井周含水层渗透性衰减还导致了水头抬升分布在井周堵塞区与主含水层交界面存在一定的折点,且该折点随着堵塞的发展愈加明显。分布曲线折点的存在主要是由于井周含水层与主含水层存在渗透差异造成的,这与均质含水层中的光滑分布曲线形成明显区别。因此,这一特征可以用于判别堵塞范围rc的大小。需要指出的是,由于本文建立的井流模型假设rc为定值,上述rc的确定方法仅适用于试井周围堵塞分布在水平和竖直方向上相对均匀的情形,而对于实际工程中可能存在的堵塞分布不均匀的问题,相关模型的建立以及堵塞范围的判定还有待进一步研究。
4. 结论
本文以井周含水层为研究对象,建立了考虑井周堵塞效应的非完整井定水头回灌井流模型。通过变量代换、Laplace变换和有限余弦Fourier变换,推导了井流模型在Laplace-Fourier空间的解,利用有限余弦Fourier逆变换及基于Stehfest法的Laplace数值逆变换得到了井流模型在实时空间的解,并通过与数值解对比证明了本文求解方法的正确性。在此基础上,本文分析了非完整井定水头回灌条件下堵塞效应对渗流场的影响规律,得到以下3点结论。
(1)较小的Kr, ∞会减小回灌过程中水头抬升和回灌流量,并降低含水层的拟稳态渗流响应,而较大的$ \lambda $仅降低了回灌过程中水头抬升和回灌流量,并不影响含水层初始和达到拟稳态时的渗流状态。
(2)受定水头回灌边界的影响,因Kr, ∞和λ不同而引起的水头差沿径向距离先增大后减小,在井周堵塞区与主含水层交界面达到最大值,较小的Kr, ∞或较大的λ均会引起水头差分布与时程曲线的增大。
(3)回灌堵塞使得水头抬升分布在井周堵塞区与主含水层交界面上存在明显的折点,造成水头在抬升过程中存在明显的下降阶段,上述特征在堵塞越严重时越显著,可为回灌堵塞的评估与预测提供参考。
-
表 1 井身结构参数
Table 1 Parameters of well structure
单位: m 试井类型 回灌压力 井径 滤管长度 滤管顶端高度 滤管底端高度 回灌井 200 0.1 10 15 5 表 2 含水层水文地质参数
Table 2 Hydrological parameters of recharged aquifer
堵塞区厚度/m 初始渗透系数/(m·h-1) 渐近渗透系数/(m·h-1) 渗透衰减速率/h-1 含水层厚度/m 储水系数 水平 竖向 水平 竖向 1.0 0.06 0.006 0.03 0.003 0.05 20 0.004 -
[1] FENG Q G, ZHAN H B. Constant-head test at a partially penetrating well in an aquifer-aquitard system[J]. Journal of Hydrology, 2019, 569: 495-505. doi: 10.1016/j.jhydrol.2018.12.018
[2] WEN Z, ZHAN H B, HUANG G H, et al. Constant-head test in a leaky aquifer with a finite-thickness skin[J]. Journal of Hydrology, 2011, 399(3/4): 326-334.
[3] YANG S Y, YEH H D. Laplace-domain solutions for radial two-zone flow equations under the conditions of constant-head and partially penetrating well[J]. Journal of Hydraulic Engineering, 2005, 131(3): 209-216. doi: 10.1061/(ASCE)0733-9429(2005)131:3(209)
[4] JACOB C E, LOHMAN S W. Nonsteady flow to a well of constant drawdown in an extensive aquifer[J]. Transactions, American Geophysical Union, 1952, 33(4): 559. doi: 10.1029/TR033i004p00559
[5] 何满潮, 刘斌, 姚磊华, 等. 地热水对井回灌渗流场理论研究[J]. 地热能, 2003, 24(2): 197-201. HE Manchao, LIU Bin, YAO Leihua, et al. Study on the theory of seepage field for geothermal single well reinjection[J]. Acta Energiae Solaris, 2003, 24(2): 197-201. (in Chinese)
[6] 何满潮, 刘斌, 姚磊华, 等. 地下热水回灌过程中渗透系数研究[J]. 吉林大学学报(地球科学版), 2002, 32(4): 374-377. HE Manchao, LIU Bin, YAO Leihua, et al. Study on hydraulic conductivity during geothermal reinjection[J]. Journal of Changchun University of Science and Technology, 2002, 32(4): 374-377. (in Chinese)
[7] THEIS C V. The relation between the lowering of the Piezometric surface and the rate and duration of discharge of a well using ground-water storage[J]. Transactions, American Geophysical Union, 1935, 16(2): 519. doi: 10.1029/TR016i002p00519
[8] 闫峭, 马聪, 周维博. 地下水回灌过程中水文地质参数的反演[J]. 灌溉排水学报, 2015, 34(7): 88-92. YAN Qiao, MA Cong, ZHOU Weibo. Hydrogeology parameters inversion during the process of groundwater recharge[J]. Journal of Irrigation and Drainage, 2015, 34(7): 88-92. (in Chinese)
[9] 李炯, 李明广, 陈锦剑, 等. 单井回灌中回灌堵塞与回灌压力波动对渗流场影响的理论研究[J]. 岩土工程学报, 2019, 41(增刊2): 226-229, 234. doi: 10.11779/CJGE2019S2057 LI Jiong, LI Minggaung, CHEN Jinjian, et al. Theoretical study on influence of well clogging and variable injection pressure on seepage field induced by single-well recharge[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 226-229, 234. (in Chinese) doi: 10.11779/CJGE2019S2057
[10] BIANCHI W C, NIGHTINGALE H I, MCCORMICK R L. Fresno, calif., subsurface drain collector-deep well recharge system[J]. Journal - American Water Works Association, 1978, 70(8): 427-435. doi: 10.1002/j.1551-8833.1978.tb04209.x
[11] YEH H D, YANG S Y, PENG H Y. A new closed-form solution for a radial two-layer drawdown equation for groundwater under constant-flux pumping in a finite-radius well[J]. Advances in Water Resources, 2003, 26(7): 747-757. doi: 10.1016/S0309-1708(03)00046-0
[12] STEHFEST H. Algorithm 368: numerical inversion of Laplace transforms[J]. Communications of the ACM, 1970, 13(1): 47-49. doi: 10.1145/361953.361969
[13] WEN Z, ZHAN H B, WANG Q R, et al. Well hydraulics in pumping tests with exponentially decayed rates of abstraction in confined aquifers[J]. Journal of Hydrology, 2017, 548: 40-45. doi: 10.1016/j.jhydrol.2017.02.046
-
期刊类型引用(0)
其他类型引用(1)
-
其他相关附件



 下载:
下载: