XFEM-based investigation on sliding regularities of soil slopes
-
摘要: 近年来对于边坡稳定的研究不再局限于安全系数的分析,而是越来越多地关注边坡可能的失稳模式和失稳过程,以提供更具针对性的防治建议。基于XFEM构造模拟土质边坡失稳滑裂过程的方法,将边坡失稳过程概化为滑裂面的发生、扩展和贯通的过程。采用黏聚裂缝模型和摩擦接触理论描述滑裂面上的接触行为,并设计一种扇形扩展控制域来表述滑裂面前端的应力集中和重分布行为,进而合理判断滑裂面的扩展时机和方向。模拟分析了一种人工设计土坡在坡顶堆载作用下的滑裂面扩展规律,比较了土体弹性模量和内摩擦角对于滑裂规律的影响。结果表明,所提方法可以合理有效地模拟边坡失稳滑裂过程,两种参数对于滑裂规律的影响符合一般认知,并根据模拟结果对推移式滑坡的发展速度和成层边坡的局部张拉裂缝给出了细观解释。Abstract: In recent years, the researches on slope stability are no longer limited to the analysis of safety factor, but more and more attention is paid to the possible failure modes and processes of slopes so as to provide more targeted prevention and control suggestions. It is aimed to establish a method for simulating the failure and sliding process of soil slopes based on the XFEM, in which the sliding process of slopes is generalized into the process of the initiation, expansion and connection of the sliding surface. The contact behavior of the sliding surface is described by the cohesive fracture model and the frictional contact theory, and a fan-shaped expansion control domain is designed to describe the stress concentration and redistribution behavior of the front end of the sliding surface so as to judge the expansion time and direction of the sliding surface reasonably. The expansion regularities of sliding surface of a manually designed soil slope with heap loading on the top are simulated and analyzed. The influences of elastic modulus and internal friction angle of soil on the sliding regularities are compared. The results show that the proposed method can simulate the failure and sliding process of soil slopes reasonably and effectively. The influences of the two parameters on the sliding regularities are consistent with the general cognition, and the simulated results may provide a mesoscopic explanation for the development speed of thrust-type landslide and the local tensile cracks of the stratified slopes.
-
Keywords:
- XFEM /
- thrust-type landslide /
- sliding surface /
- stratified soil slope /
- sliding regularity
-
0. 引言
边坡失稳在大多数情况下不是瞬间发生整体破坏,而是由局部滑移破坏逐步发展至整体贯通破坏的过程[1]。由于成因不同导致滑坡的表现形式各异,人工开挖或库水位骤降一般会引起由前缘启动向后缘发展的滑坡,称为牵引式滑坡[2-4];坡顶堆载或降雨可能引发由后缘启动向前缘发展的滑坡,称为推移式滑坡[5-6]。相比于牵引式滑坡,推移式滑坡在破坏前坡顶会有明显的预警变形,“塑性”破坏的特点更加明显[7]。
传统的极限平衡法(LEM)只能分析边坡的安全系数而无法计算边坡整体的应力变形情况,且需要假设滑裂面的形状和位置;弹塑性有限元方法(FEM)在变形过大的情况下引起网格畸变,也难以准确刻画边坡的滑裂面发展规律。
近年来,很多学者提出了多种更贴合实际的分析方法。王庚荪等[8]提出了一种含剪切带的单元模型并将其应用于边坡破坏的过程分析,是国内较早对边坡渐近破坏过程的模拟研究;唐芬等[9]针对强度折减法采用单一安全系数对强度参数进行折减的不足,提出了对c,φ采用不同的折减系数的双安全系数方法,但是仍未能在行业内达到普遍共识;Conte等[10]在有限元法中采用非局部弹黏塑性本构模型用以克服不收敛和网格依赖性等问题,进而模拟应变软化边坡剪切带的发展和边坡破坏过程;Mohammadi等[11]采用大变形有限元法模拟了边坡破坏过程中的变形情况;卢应发等[12-13]建立了一种全新的条块力-位移分析方法,并提出几种有针对性的边坡稳定性系数计算方法;沈华章等[14]、薛海斌等[15]提出了一种基于矢量和法并考虑应变软化的边坡破坏分析方法。然而上述方法受到传统有限元框架所限,难免引入各种假定,而且模拟效果仍不够直观。
扩展有限元法(XFEM)是近些年发展出的不需要网格重构而可以模拟裂缝、剪切带等不连续场的有效方法,正得到广泛的应用[16-19]。滑坡问题中包含不连续位移场,用XFEM进行研究分析与传统方法相比不需要假定滑裂面的形状和位置,程序可自行搜索和模拟滑裂面的发生发展过程,而且克服了网格畸变问题。
本文基于XFEM构造模拟土质边坡滑裂面发生发展过程的方法,并讨论材料参数对均质土坡推移式滑动的滑裂面深度和滑裂面形态的影响,在此基础上研究成层土坡推移式滑动的滑裂面扩展规律。
1. XFEM方法介绍
1.1 不连续位移场的构造
XFEM通过对有限元计算域内部分结点富集额外自由度来构造非连续场。对于非连续位移场,利用常规自由度插值构造的连续位移场 {\boldsymbol{u}^{{\text{cont}}}} 叠合富集自由度构造的不连续位移场 {\boldsymbol{u}^\text{disc}} 来描述:
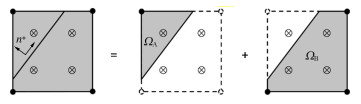
\boldsymbol{u} = \underbrace {\sum\limits_{I \in \psi } {{\boldsymbol{N}_I}(\boldsymbol{x})\boldsymbol{u}_I^{}} }_{{\boldsymbol{u}^{{\text{cont}}}}} + \underbrace {\sum\limits_{I \in \xi } {{\boldsymbol{N}_I}(\boldsymbol{x})\boldsymbol{q}_I^{}(H - H_I^{})} }_{{\boldsymbol{u}^\text{disc}}} 。 (1) 式中ψ为域内所有结点的集合,ξ为域内富集结点的集合, \xi \subset \psi ; \boldsymbol{N}(\boldsymbol{x}) 为形函数;u为常规结点位移向量;q为富集结点位移向量;H为Heaviside阶跃函数,且
H(x) = \left\{ {\begin{array}{*{20}{c}} 1&{(x \in {\varOmega _{\text{A}}})} \\ 0&{(x \in {\varOmega _{\text{B}}})} \end{array}} \right. \text{,} (2) 其中, {\varOmega _{\text{A}}} 和 {\varOmega _{\text{B}}} 分别为单元内不连续面切割而成的两个子域,如图 1所示。虽然在整个单元上由于存在不连续面,其位移场和其他场函数也都是不连续的,但是在两个子域上这些场函数是连续的,因而可以将单元积分在两个子域内分别进行[20]。
1.2 控制方程
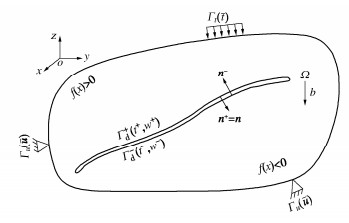
边坡失稳产生滑裂面的过程可视为一种具有内部演化界面的初边值问题,不失一般性,如图 2所示。研究域为 \varOmega ,b为域内体力。{\varGamma _t}为力边界,其上作用 \boldsymbol{\bar t} ,{\varGamma _u}为位移边界,满足\boldsymbol {u = \bar u} ,且{\varGamma _t} \cap {\varGamma _u} = \emptyset 。{\varGamma _{\rm{d}} }表示裂缝,为内部边界,分为\varGamma _{\rm{d}} ^ + 和\varGamma _{\rm{d}} ^ - 两个界面,即{\varGamma _{\rm{d}} } = \varGamma _{\rm{d}} ^ + \cup \varGamma _{\rm{d}} ^ - , {\boldsymbol{n}^ + } , {\boldsymbol{w}^ + } , {\boldsymbol{t}^ + } 和 {\boldsymbol{n}^ - } , {\boldsymbol{w}^ - } , {\boldsymbol{t}^ - } 分别对应界面上的法向量、位移向量和应力向量。
在保守力系作用下,由虚功原理可得到准静态动量方程的等效积分弱形式:
\begin{aligned} \int_{\varOmega \backslash {\varGamma _{\rm{d}}}}^{} {\delta \boldsymbol{\varepsilon} :\boldsymbol{\sigma} } {\text{d}}\varOmega = &\int_\varOmega ^{} {\delta \boldsymbol{u} \cdot \boldsymbol{b}} {\text{d}}\varOmega + \int_{{\varGamma _t}}^{} {\delta \boldsymbol{u} \cdot } \boldsymbol{\bar t}{\text{d}}\varGamma + \\ &\int_{\varGamma _{\rm{d}}^ - }^{} {\delta {\boldsymbol{w}^ - } \cdot {\boldsymbol{t}^ - }} {\text{d}}\varGamma + \int_{\varGamma _{\rm{d}}^ + }^{} {\delta {\boldsymbol{w}^ + } \cdot {\boldsymbol{t}^ + }} {\text{d}}\varGamma \text{,} \end{aligned} (3) 式中,σ和ε分别为应力张量和应变张量。
裂缝面上的本构方程为
\boldsymbol{t}_{}^ + = \boldsymbol{t}_{}^ + ({\boldsymbol{w}^ - } - {\boldsymbol{w}^ + }) = \boldsymbol{t}_{}^ + (\Delta {\left. \boldsymbol{u} \right|_{\varGamma _{\rm{d}}^{}}}) = {\boldsymbol{Q}^{\rm{T}}}{\boldsymbol{D}_\varGamma }\boldsymbol{Q}\Delta {\left. \boldsymbol{u} \right|_{\varGamma _{\rm{d}}^{}}} \text{,} (4) 式中, {\boldsymbol{D}_\varGamma } 为局部坐标下的裂缝本构矩阵,Q为局部坐标与全局坐标的转换矩阵。
根据虚位移原理,分别对式(3)中u和q取变分,可整理得到控制方程的有限元格式:
\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{K}_{uu}}}&{{\boldsymbol{K}_{uq}}} \\ {{\boldsymbol{K}_{qu}}}&{{\boldsymbol{K}_{qq}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \boldsymbol{u} \\ \boldsymbol{q} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{\boldsymbol{K}_{qq}^{{\varGamma _{\rm{d}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \boldsymbol{u} \\ \boldsymbol{q} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{F}_u}} \\ {{\boldsymbol{F}_q}} \end{array}} \right] \text{,} (5) 式中, {\boldsymbol{K}}_{uu}={\displaystyle {\int }_{\varOmega }{\boldsymbol{B}}^{\rm{T}}\boldsymbol{DB}\text{d}\varOmega },{\boldsymbol{K}}_{qu}\boldsymbol{=}{\boldsymbol{K}}_{uq}{}^{\rm{T}}={\displaystyle {\int }_{\varOmega }{\boldsymbol{B}}^{\rm{T}}\boldsymbol{DB}(\boldsymbol{H}-} {\boldsymbol{H}}_{I})\text{d}\varOmega ,{\boldsymbol{K}}_{qq}={\displaystyle {\int }_{\varOmega }{(\boldsymbol{H}-{\boldsymbol{H}}_{I})}^{\rm{T}}{\boldsymbol{B}}^{\rm{T}}\boldsymbol{DB}(\boldsymbol{H}-{\boldsymbol{H}}_{I})\text{d}\varOmega },{\boldsymbol{K}}_{qq}^{{\varGamma }_{d}}= \int_{\varGamma_{\mathrm{d}}} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{D}_{\Gamma} \boldsymbol{Q} \boldsymbol{N} \mathrm{d} \varGamma_{\mathrm{d}}, \quad \boldsymbol{F}_u=\int_{\varOmega} \boldsymbol{N}^{\mathrm{T}} \boldsymbol{b} \mathrm{d} \varOmega+\int_{\varGamma_t} \boldsymbol{N}^{\mathrm{T}} \overline{\boldsymbol{t}} \mathrm{d} \varGamma, \quad \boldsymbol{F}_q= {\displaystyle {\int }_{\varOmega }{(\boldsymbol{H}-{\boldsymbol{H}}_{I})}^{\rm{T}}{\boldsymbol{N}}^{\rm{T}}\boldsymbol{b}}\mathrm{d}\varOmega +{\displaystyle {\int }_{{\varGamma }_{t}}{\left(\boldsymbol{H}-{\boldsymbol{H}}_{I}\right)}^{\rm{T}}{\boldsymbol{N}}^{\rm{T}}\boldsymbol{\bar{t} }}\mathrm{d}\varGamma 。
1.3 界面接触算法
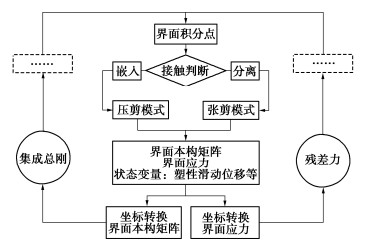
在形成滑裂面后,滑裂面两侧位移不连续,可以相互错动或者分离,即压剪模式或张剪模式;滑裂面两侧的应力联系通过接触算法实现,本研究在裂缝界面处于张剪状态时采用黏聚裂纹模型[21],在处于压剪状态时采用Willner的摩擦接触理论[22]。相对位移可以分为沿着滑裂面法向的正相对位移{w_{\text{n}}}和沿着滑裂面切向的切相对位移{w_{\text{s}}}。
图 3给出了接触算法流程。在每一迭代步中,首先判断相对位移模式:若{w_{\text{n}}}>0,表示接触点上的裂缝面相互嵌入,采用压剪模式对其进行计算;若{w_{\text{n}}}<0,表示接触点上的裂缝面相互远离,采用张剪模式对其进行计算。接触算法在集成总刚时,会给出 {\boldsymbol{D}_\varGamma } 矩阵,在应力积分时,会给出接触应力{t_\text{n}}和{t_\text{s}},进而参与残差平衡计算。
1.4 土体的滑裂判别
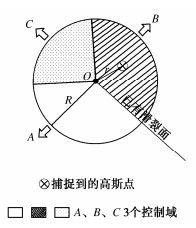
土体滑裂面尖端和裂缝尖端类似,会产生应力集中和应力主轴偏转。然而土体材料由于其碎散性和弹塑性,一般应力集中程度不高,因此可以利用尖端的一个局部区域中的特征应力状态来判断滑裂面的扩展条件,称这个局部区域为扩展控制域。基于此设置扇形扩展控制域如图 4所示,C扇面位于缝尖的正前方以判定张拉裂缝为主,圆心角为90°,A,B扇面对称于裂缝两侧以判断剪切裂缝为主,圆心角均为135°。每个扇形控制域的特征应力状态由域内所有积分点的应力加权平均得到,其中权函数为
w = \exp \left( { - \frac{{{r^5}}}{{{R^5}}}} \right)\text{,} (6) 式中,r为控制区域内某积分点到缝尖O点的距离,R为扩展控制域的半径,建议取为1.5倍~3倍的网格特征长度。
对于张拉破坏采用最大拉应力准则;对于剪切破坏采用Mohr-Coulomb准则。分别计算尖端A、B、C扩展控制域的拉应力水平TL和剪应力水平SL:
{T_{\text{L}}} = \left| {\frac{{{\sigma _3}}}{{{f_{t} }}}} \right|{\text{ }}({\sigma _3} < 0)\text{,} (7) {S_{\text{L}}} = \frac{{{\sigma _1} - {\sigma _3}}}{{\sin \varphi ({\sigma _1}{\text{ + }}{\sigma _3} + {{2c} \mathord{\left/ {\vphantom {{2c} {\tan \varphi }}} \right. } {\tan \varphi }})}}\text{,} (8) 式中,σ1为大主应力,σ3为小主应力,ft为土体的抗拉强度,φ为土体的内摩擦角,c为土体的黏聚力。当任意扩展控制域内的任意一种应力水平达到1,则当前控制域内发生相应类型的破坏,这个控制域称为“优势控制域”。当{\sigma _3}<0且TL=1时,出现张拉破坏面,扩展方向为垂直于小主应力的方向;当SL=1时,出现与小主应力方向成φ/2+45°角的剪切破坏面,具体扩展方向需要根据已有滑裂面进一步判断[16]。此处引入两个设定条件:①惯性条件,即宏观裂缝向前扩展时总是趋向于沿着与已有裂缝最接近的方向进行;②区域占优假定,即裂缝扩展方向优先落在“优势控制域”内。当两个假定不能同时满足时,优先满足区域占优假定,但不应出现大于90°的转角。
2. 推移式滑坡的滑裂面扩展规律研究
土质边坡的滑裂破坏除了受到结构形式和荷载条件等外在因素影响外,土体自身的变形特性(模量)和强度特性(内摩擦角和黏聚力)也至关重要,可以归结为内在因素。本文基于人工设计理想边坡,对土体材料采用Mohr-Coulomb理想弹塑性本构模型,分析弹性模量和内摩擦角对土质边坡滑裂破坏过程的影响。
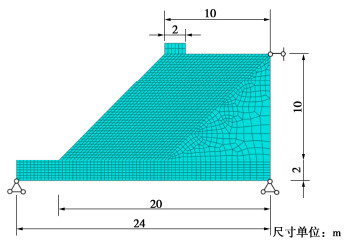
土坡模型和计算网格如图 5所示,地基厚2 m,长24 m;土坡底部长20 m,顶部长10 m,高10 m;在土坡顶部的边缘有一长2 m、高1 m的刚性块,用于加载制造土坡滑裂破坏,计算采用四结点四边形平面应变单元。对地基的底部施加全位移约束,对地基的左右两侧和土坡的右侧施加水平位移约束。
土体基本材料参数为:弹性模量E为10 MPa,泊松比\nu 为0.4,重度 \gamma 为20.0 kN/m3,内摩擦角φ为10°,黏聚力c为30 kPa,抗拉强度ft为20 kPa。计算过程分为两个步骤:步骤1对整个模型施加重力荷载进行自重平衡计算;步骤2首先进行位移清零,然后在刚性块的中心施加竖直向下的位移荷载u= 0.5 m,分成100个增量步进行。
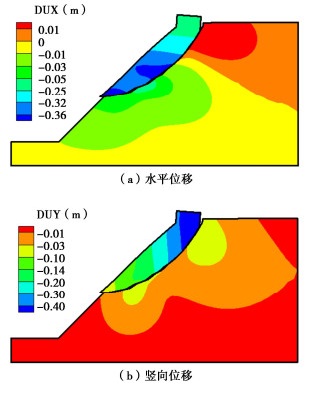
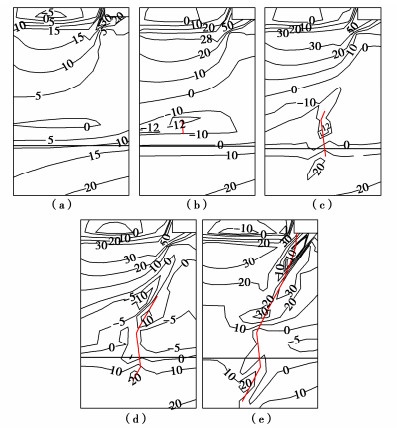
基本材料参数的模拟结果如图 6所示。滑裂面首先从顶部加载后缘产生,然后逐步向下发展,直至贯通坡面,形成整体滑动。在第22个加载步完成后滑裂面已经贯通滑体,此时滑坡体中上部表现为以沉降变形为主,而滑坡体中下部表现为以横向挤出变形为主。之后滑体将发生大滑移变形,边坡完全失稳破坏。
2.1 均质土坡推移式滑动的滑裂面扩展规律
(1)弹性模量对均质土坡滑裂面的影响
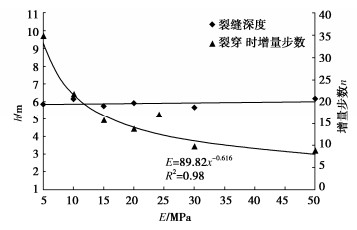
分析不同弹性模量下均质土坡推移式滑裂面的滑裂深度和贯通所需增量步数的变化规律。选取弹性模量分别为5,10,15,20,30,50 MPa,其他参数不变,结果汇总如图 7所示。纵坐标为滑裂深度h(滑裂面最低点到土坡顶部的竖直距离)和滑裂面贯穿时的加载增量步数n,横坐标为弹性模量E。结果显示,弹性模量对均质土坡推滑破坏的滑裂面深度影响很小,不同的弹性模量,其他条件相同的均质土坡得到几乎相同的滑裂深度。但弹性模量越大,滑裂面贯穿时的增量步数越少,即总的加荷量越小。这一规律说明均质土坡的推移破坏是由应力和强度控制,而非变形控制,也说明了本文的强度控制区域占优判别的扩展分析方法符合问题的实际物理机制。
(2)内摩擦角对均质土坡滑裂面的影响
分析不同内摩擦角下均质土坡推移式滑裂面的滑裂深度和贯通所需增量步数的变化规律,选取内摩擦角的变化区间为5°~26°,其他参数不变。
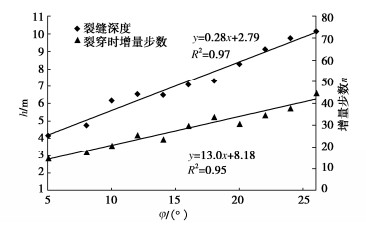
计算结果汇总如图 8所示,其中纵坐标分别为滑裂面深度h和滑裂面贯穿时的增量步数n,横坐标为内摩擦角φ。由图 8可见,均质土坡推移式滑动的滑裂面深度随着土体内摩擦角的增大而近似线性增加,且滑裂面贯穿需要的位移荷载也近似线性增加,两者的斜率分别为0.28和1.30。
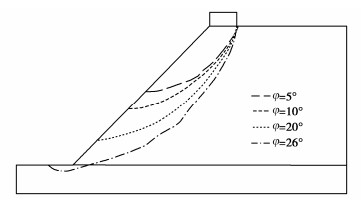
部分算例的具体滑裂面形态如图 9所示。由图 9可以看出,较大的内摩擦角会产生更深的滑裂路径,提高边坡抗滑力和整体稳定性,结果符合一般认知规律。
(3)滑裂面扩展过程中反力的变化
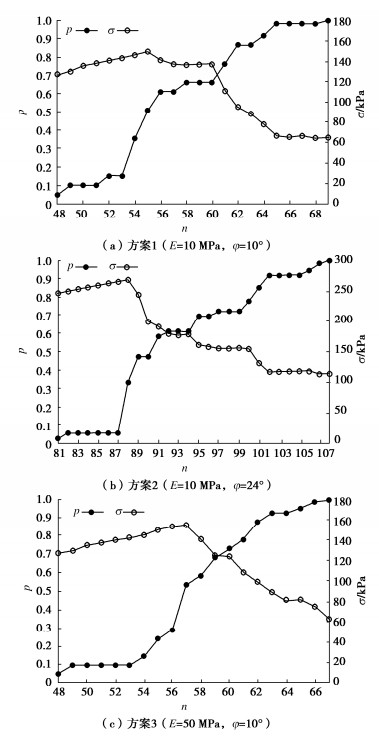
选取位于刚性块中心正下方的土体单元作为对象,研究滑裂面扩展过程中反力的变化。设计了3个计算方案:方案1,E = 10 MPa,φ = 10°;方案2,E = 10 MPa,φ = 24°;方案3,E = 50 MPa,φ = 10°。计算结果见图 10,其中n为计算的增量步数(3种方案的总增量步数均为120步,总位移荷载会根据弹性模量确定,以保证每一增量步内的外力增量保持不变),p为当前增量步下的滑裂面深度与总裂缝深度的比值, \sigma 为对象单元的竖向应力。
由图 10可知,在滑裂面开裂前和刚开裂的一段时间内,对象单元的竖向正应力随着增量步数的增加而增加;当滑裂面扩展到一定深度后,滑裂面向前的扩展总是伴随着反力的减小。这说明推移式滑坡演化过程至少分为2个阶段:后缘压缩阶段和加速变形阶段。对于土体模量较小的情况,在加速变形阶段可能会产生多个变形台阶,滑裂面贯通的突发性较弱。对于土体模量较大的情况,加速变形阶段会使滑裂面直接贯穿坡体,边坡失稳的突发性较强。内摩擦角越大,在加速变形阶段越可能产生的变形台阶数量越多,有利于减弱边坡失稳的突发性。
2.2 成层土坡推移式滑动的滑裂面扩展规律
设计材料分界面分别距离土坡顶部2.5,7.5 m的两个成层土坡。计算过程分为两个步骤:①对整个模型施加重力荷载;②分成120个增量步,在刚性块的中心施加竖直向下的位移荷载u = 0.3 m。
(1)弹性模量对成层土坡滑裂面的影响
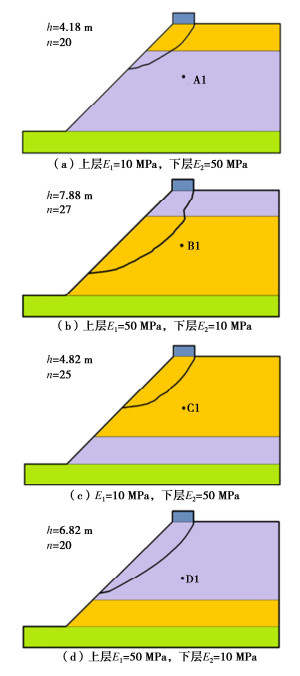
地基中土体内摩擦角φ为16°。将位于材料分界面上部的材料的弹性模量记为E1,位于材料分界面下部的材料的弹性模量记为E2。对上下分界面分别计算“E1 = 10 MPa,E2 = 50 MPa”和“E1 = 50 MPa,E2 = 10 MPa”两种工况,其他参数不变,得到滑裂面形态如图 11所示。
比较图 11(a),(b)与图 11(c),(d)可知:如果上部土体的弹性模量比下部土体的小,则滑裂面深度较小;反之,则滑裂面深度较大。比较图 11(a),11(c)及图 11(b),(d)可知:土体为上软下硬的情况时,上部土层越厚,则滑裂面的深度越大;土体为上硬下软的情况时,上部土层越厚,则滑裂面的深度越小。这一规律与刚性基础基底应力分布规律类似,即上软下硬的边坡发生应力集中,破坏集中在较小范围内;而上硬下软的边坡发生应力扩散,破坏范围也相应扩大。
图 11(b)中,在材料分界面处滑裂面路径发生了较大的变化,是由于这一区域发生了局部张拉破坏,且滑裂面并非是由上缘向下单向发展而成的,这将在第3节中详细分析。
(2)内摩擦角对成层土坡滑裂面的影响
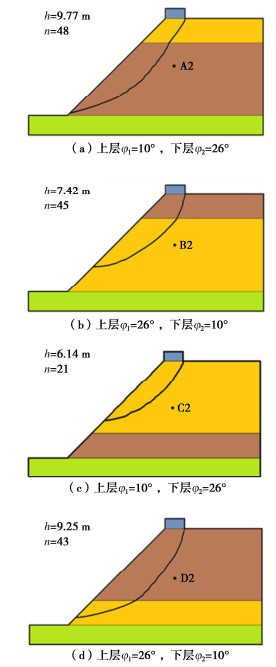
将成层土坡上部土体的内摩擦角记为φ1,下部土体的内摩擦角记为φ2。对两个成层土坡分别计算“φ1 = 10°,φ2 = 26°”和“φ1 = 26°,φ2 = 10°”时的推滑破坏过程,共4种工况,其他参数和方案设置不变,计算得到最终贯通后的滑裂面形态如图 12所示。由图 12可见,与均质土坡类似,整体较大的内摩擦角会产生较深的滑裂面,从而提高边坡的整体安全系数。对于成层土坡,内摩擦角大的土层占总体比例越大(相当于整体的加权平均内摩擦角越大),则最终整体的滑裂深度越大,边坡越趋于安全。
3. 成层土坡中张拉裂缝的分析
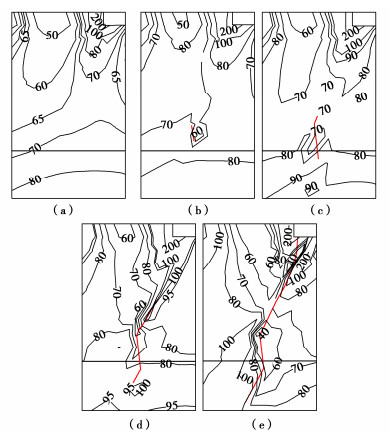
第2节在不同弹性模量的成层土坡推滑破坏过程中,分界面附近出现了张拉型裂缝,如图 11(b)所示。对此过程中的应力分布变化进行分析,分别绘出此工况下滑裂面扩展过程中5个典型阶段的大主应力和小主应力分布,如图 13,14所示。
在滑裂面出现之前,刚性块施加的位移荷载使土坡不断向下压缩,由于材料分界面上方土体的弹性模量比下方土体的大,所以下方土体的变形会更大,而在分界面处两者要满足变形协调条件,导致上方土体内产生拉应力。当拉应力超过土体的抗拉强度,就会发生张拉裂缝。之后随着进一步加载和滑裂面发展,滑裂面尖端远离分界面,转变为剪切破坏。
综上分析,图 13(a)~(e),14(a)~(e)给出的滑裂面发展过程为:①加载初期,分层界面上下大主应力分布较为均匀,是以自重应力为主,而上层较硬土体的底部因为变形不协调已经开始出现横向拉应力;②上层土体底部附近出现张拉裂缝;③张拉裂缝向两端扩展;④张拉裂缝两端的应力分布发生变化,剪切应力开始起主导作用,裂缝方向也随之发生转折;⑤剪切裂缝继续发展,向上贯通到破顶加载刚性块的角部附近,向下也继续延伸,直至最终形成贯穿整个滑体的滑裂面。
4. 结论
本文基于XFEM开发了能够模拟土体滑裂面扩展过程的程序。通过对人工设计均质土坡和成层土坡的推滑破坏过程进行模拟分析,并比较土体弹性模量和内摩擦角的影响,得到以下6点结论。
(1)坡顶堆载作用下,滑裂面从顶部加载后缘产生,然后逐步向下发展,直至贯通坡面,形成整体滑动。
(2)弹性模量对均质土坡推移式滑动的滑裂面深度的影响很小,但弹性模量越大,滑裂面贯穿的所需的加载量越少,即更容易形成贯通滑裂。
(3)均质土坡推移式滑动的滑裂面深度随着土体内摩擦角的增大而增大,滑裂面贯穿需要的加载量也随之增大。内摩擦角同时影响着滑裂面的扩展角度和开裂时机。
(4)推移式滑坡演化过程可分为后缘压缩和加速变形两个阶段。土体模量较小时,在加速变形阶段可能会产生多个变形台阶,滑裂面贯通的突发性较弱;土体模量较大时,加速变形阶段滑裂面较快贯通,失稳的突发性较强。内摩擦角越大,则在加速变形阶段可能的变形台阶数越多,从而降低失稳的突发性。
(5)对于成层土坡,上软下硬的边坡发生应力集中,破坏集中在较小范围内,滑裂深度较小;而上硬下软的边坡发生应力扩散,破坏范围也相应扩大,滑裂深度较大。成层土坡的整体(加权平均)内摩擦角越大,则滑裂深度越大。
(6)成层土坡在层间模量相差较大的情况产生局部变形不协调而发生局部的张拉型破坏,进而影响整体的边坡滑裂破坏过程。
这些规律均符合一般认知,也验证了本文方法可以准确、直观地模拟滑裂面的发生发展过程,并提供细观机理上的认识。扩展有限元方法在岩土工程问题中值得进一步更为广泛的应用研究。
-
-
[1] SKEMPTON A W. Long-term stability of clay slopes[J]. Géotechnique, 1964, 14(2): 77-102. doi: 10.1680/geot.1964.14.2.77
[2] 卢应发, 邓国栋, 杨丽平, 等. 滑坡关键块力学行为及力传递特征和不同应力状态的稳定系数研究[J]. 岩石力学与工程学报, 2014, 33(5): 884-891. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201405003.htm LU Ying-fa, DENG Guo-dong, YANG Li-ping, et al. Study of mechanical behaviors of key blocks and characteristics of force transmit and stability coefficient of different stress states of landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 884-891. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201405003.htm
[3] 宋东日, 任伟中, 沈波, 等. 牵引式滑坡的破坏机制及其加固措施探讨: 以某高速公路牵引式滑坡为例[J]. 岩土力学, 2013, 34(12): 3587-3593. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312037.htm SONG Dong-ri, REN Wei-zhong, SHEN Bo, et al. Discussion on failure mechanism of retrogressive landslide and its reinforcement measures: taking a certain expressway retrogressive landslide for example[J]. Rock and Soil Mechanics, 2013, 34(12): 3587-3593. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312037.htm
[4] 周跃峰, 龚壁卫, 胡波, 等. 牵引式滑坡演化模式研究[J]. 岩土工程学报, 2014, 36(10): 1855-1862. doi: 10.11779/CJGE201410013 ZHOU Yue-feng, GONG Bi-wei, HU Bo, et al. Evolution mode of retrogressive landslide[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(10): 1855-1862. (in Chinese) doi: 10.11779/CJGE201410013
[5] 雍睿, 胡新丽, 唐辉明, 等. 推移式滑坡演化过程模型试验与数值模拟研究[J]. 岩土力学, 2013, 34(10): 3018-3027. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201310039.htm YONG Rui, HU Xin-li, TANG Hui-ming, et al. Model testing and numerical simulation study of evolutionary process of thrust load caused landslide[J]. Rock and Soil Mechanics, 2013, 34(10): 3018-3027. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201310039.htm
[6] 邬爱清, 丁秀丽, 李会中, 等. 非连续变形分析方法模拟千将坪滑坡启动与滑坡全过程[J]. 岩石力学与工程学报, 2006, 25(7): 1297-1303. doi: 10.3321/j.issn:1000-6915.2006.07.001 WU Ai-qing, DING Xiu-li, LI Hui-zhong, et al. Numerical simulation of startup and whole failure process of qianjiangping landslide using discontinuous deformation analysis method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1297-1303. (in Chinese) doi: 10.3321/j.issn:1000-6915.2006.07.001
[7] 杨光华, 钟志辉, 张玉成, 等. 滑坡灾害的机制与力学特性分析[J]. 岩石力学与工程学报, 2016, 35(增刊2): 4009-4017. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S2062.htm YANG Guang-hua, ZHONG Zhi-hui, ZHANG Yu-cheng, et al. Analysis of mechanism and mechanical characteristics of landslide disaster[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S2): 4009-4017. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S2062.htm
[8] 王庚荪, 孔令伟, 郭爱国, 等. 含剪切带单元模型及其在边坡渐进破坏分析中的应用[J]. 岩石力学与工程学报, 2005, 24(21): 3852-3857. doi: 10.3321/j.issn:1000-6915.2005.21.008 WANG Geng-sun, KONG Ling-wei, GUO Ai-guo, et al. Element model with shear band and its application to progressive failure analysis of slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(21): 3852-3857. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.21.008
[9] 唐芬, 郑颖人, 赵尚毅. 土坡渐进破坏的双安全系数讨论[J]. 岩石力学与工程学报, 2007, 26(7): 1402-1407. doi: 10.3321/j.issn:1000-6915.2007.07.013 TANG Fen, ZHENG Ying-ren, ZHAO Shang-yi. Discussion on two safety factors for progressive failure of soil slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1402-1407. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.07.013
[10] CONTE E, SILVESTRI F, TRONCONE A. Stability analysis of slopes in soils with strain-softening behaviour[J]. Computers and Geotechnics, 2010, 37(5): 710-722. doi: 10.1016/j.compgeo.2010.04.010
[11] MOHAMMADI S, TAIEBAT H A. A large deformation analysis for the assessment of failure induced deformations of slopes in strain softening materials[J]. Computers and Geotechnics, 2013, 49: 279-288. doi: 10.1016/j.compgeo.2012.08.006
[12] 卢应发, 黄学斌, 刘德富. 边坡稳定分析条块力-位移法及其应用[J]. 岩土力学, 2015, 36(10): 2787-2798. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510007.htm LU Ying-fa, HUANG Xue-bin, LIU De-fu. Slice block force-displacement method of slope stability analysis and its application[J]. Rock and Soil Mechanics, 2015, 36(10): 2787-2798. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510007.htm
[13] 卢应发, 刘德富. 一种边坡渐进破坏潜在滑动面的计算方法: CN105335607A[P]. 2016-02-17. LU Ying-fa, LIU De-fu. Slope Progressive Failure Latent Slide Surface Calculating Method: CN105335607A[P]. 2016-02-17. (in Chinese)
[14] 沈华章, 王水林, 郭明伟, 等. 应变软化边坡渐进破坏及其稳定性初步研究[J]. 岩土力学, 2016, 37(1): 175-184. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201601022.htm SHEN Hua-zhang, WANG Shui-lin, GUO Ming-wei, et al. A preliminary study of the progressive failure and stability of slope with strain-softening behaviour[J]. Rock and Soil Mechanics, 2016, 37(1): 175-184. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201601022.htm
[15] 薛海斌, 党发宁, 尹小涛, 等. 应变软化边坡稳定性分析方法研究[J]. 岩土工程学报, 2016, 38(3): 570-576. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201603026.htm XUE Hai-bin, DANG Fa-ning, YIN Xiao-tao, et al. Stability analysis methods for strain-softening slopes[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 570-576. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201603026.htm
[16] MOËS N, DOLBOW J, BELYTSCHKO T. A finite element method for crack growth without remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 46(1): 131-150. doi: 10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J
[17] FRIES T P, BELYTSCHKO T. The extended/generalized finite element method: an overview of the method and its applications[J]. International Journal for Numerical Methods in Engineering, 2010, 84(3): 253-304. doi: 10.1002/nme.2914
[18] 余天堂. 扩展有限单元法: 理论、应用及程序[M]. 北京: 科学出版社, 2014. YU Tian-tang. Extended Finite Element Method: Theory, Application and Program[M]. Beijing: Science Press, 2014. (in Chinese)
[19] 喻葭临. 土中剪切带扩展机理研究和扩展过程模拟[D]. 北京: 清华大学, 2009. YU Jia-lin. Mechanism Investigation and Numerical Simulation of Evolution of Shear Band in Soil[D]. Beijing: Tsinghua University, 2009. (in Chinese)
[20] 王翔南. 土体裂缝演化过程的扩展有限元法模拟[D]. 北京: 清华大学, 2018. WANG Xiang-nan. XFEM Simulation of Crack Evolution in Earth Structures[D]. Beijing: Tsinghua University, 2018. (in Chinese)
[21] PLANAS J, ELICES M, GUINEA G V, et al. Generalizations and specializations of cohesive crack models[J]. Engineering Fracture Mechanics, 2003, 70(14): 1759-1776. https://www.sciencedirect.com/science/article/pii/S0013794403001231
[22] 胡斌. 现代接触动力学[M]. 南京: 东南大学出版社, 2003. HU Bin. Advanced Contact Dynamics[M]. Nanjing: Southeast University Press, 2003. (in Chinese)
-
期刊类型引用(5)
1. 楼晓明,孙逸玮,张蓟. 软土地基沟渠开挖诱发远处围堰失稳的实例分析. 水利水电技术(中英文). 2024(S1): 151-159 .  百度学术
百度学术
2. 高玉峰,王玉杰,张飞,姬建,陈亮,倪钧钧,张卫杰,宋健,杨尚川. 边坡工程与堤坝工程研究进展. 土木工程学报. 2024(08): 97-118 .  百度学术
百度学术
3. 郭双枫,何嘉元,张志华,张鹏,李宁,朱锐. 双层土质滑坡临界滑动面判识与失稳机理研究. 防灾减灾工程学报. 2024(05): 1020-1029 .  百度学术
百度学术
4. 穆保岗,王志强. 考虑坡顶裂隙分布特征的包山墙稳定性研究. 特种结构. 2023(02): 1-7 .  百度学术
百度学术
5. 李生清. 基于GA-Sarma算法的边坡最不利滑裂面搜索方法. 地质与勘探. 2022(04): 887-894 .  百度学术
百度学术
其他类型引用(5)



 下载:
下载: