Re-examination of dynamic load tests on piles
-
摘要: 桩的动力载荷试验（DLT）和快速载荷试验（RLT）都追求桩的承载力在试验时能充分激发，也都通过桩顶的冲击和响应信号测量、分析，判定桩的承载力。但两种试验对落锤或等效配重的重量要求相差3~5倍，依据的力学原理各异。基于传统的桩-土计算模式与落锤结合建立的锤-桩-土系统相互作用模型，通过波动力学分析、动量定理验证和实测案例对比表明：锤的动量和能量传递除与桩周岩土阻力大小有关外，还明显受锤与桩的阻抗比或质量比、桩的侧阻和端阻分布形式影响。研究了不同桩侧或桩端阻力、不同阻抗比对能量传递和冲量变化的影响规律，分析了与桩的承载能力高低相关的“桩对锤冲顶”、“溜桩”和“等能量条件下嵌岩桩的端阻力发挥效率高于静载试验”等动力学现象，充实了动力试桩的理论基础，分析了RLT的原理缺陷，提出了DLT与RLT相互融合的建议。Abstract: The dynamic load test (DLT) and the rapid load test (RLT) on piles both pursue the full activation of pile capacity during the impact event and evaluate the pile capacity by measuring and analyzing the impact excitation and response signals of pile top. However, the both tests require 3~5 times different weights of drop mass or inertial reaction mass as well as distinct mechanical principles. Based on the hammer-pile-soil interaction model established under the combination of the traditional pile-soil interaction mode and the drop mass system, the analysis of wave mechanics, the proof of momentum theorem and the comparison of test cases show that the momentum and energy transfer of the hammer are related to the compressive resistance of the pile and influenced by the impedance ratio or mass ratio of the hammer and the pile and the side/tip resistance distribution of the pile. The influences of different side/tip resistances and impedance ratios on the energy transfer and impulse change and the dynamic phenomena relating to the level of the pile capacity, "pile-to-hammer bump", "pile run-away"and "higher efficiency of tip resistance mobilization for piles resting on hard bedrock than that of the static load tests under the equivalent energy consumption circumstances" are analyzed, which enriches the dynamic load tests on the piles. The principle defects of RLT are analyzed, and the integration of DLT and RLT is suggested.
-
0. 引言
基桩动力检测DLT在国际上特指采用重锤对桩冲击，测量和分析应力波在桩身中传播的力学行为，进而判定桩的承载能力、桩身结构完整性和桩锤能效等指标的检测活动。中国对DLT的称谓仍与美国一致，叫做高应变动力检测。40年DLT的应用实践表明，由于锤与桩-土系统相互作用机理的客观复杂性，重锤冲击下桩的承载性状计算分析，并非一个孤立的波动方程数值求解步骤，而是从应力波测量方案制订开始到实施，再从波形计算分析到检测结论出具，每个操作环节都离不开波动力学与桩基设计相互协调、与岩土工程经验相互印证。根据打桩总阻力的波动方程解析解，CASE法桩的静阻力（承载力）计算公式推导[1]，假定桩侧土阻力波在入射和反射两个半程相等，整桩土的动阻力仅与桩端运动速度成正比，且可由一个与桩持力层土的简单物理分类（颗粒级配或塑性指数）定名有关的经验阻尼系数Jc进行修正。可以想见，即使在桩基条件相近的局部地区，面对不止一个对桩承载性状有影响且分类定名不同的桩周岩土层，单一的Jc很难具有代表性，加之CASE法公式推导的近似简化，Jc变成了一个集土的力学特性和桩身波传播机制修正功能于一身的综合调整系数。故CASE法在中国应用约10 a，该法推荐的Jc取值就基本被摒弃，波形信号拟合变成了桩承载力计算方法的主流[2]。不过，信号拟合仍需对桩-土系统建模，即使有静动对比，也只有桩的静阻力-变形模型及其参数的合理性能被验证，而体现动阻力发挥机制的阻尼型式及其取值，如Smith型静动耦合阻尼，多年研究仍停留在砂土取值低、黏性土取值高的定性认知上[3]。
足够的冲击能量是充分发挥桩周岩土阻力的前提，宏观表现是桩“被打动”或产生明显贯入度。根据波动理论，桩-土系统的广义阻抗是系统抵抗激励使其产生运动的能力表征，分为速度型阻抗和位移型阻抗，前者与桩身横截面力学阻抗和桩周岩土动阻力正相关，后者是桩周岩土静阻力高低的体现。“重锤低击”是保证DLT试验有效性的原则，相反“轻锤高击”将在桩身产生更强的锤击拉、压应力，造成桩身结构损伤，同时随着锤重减轻，锤与桩-土系统的不匹配程度加剧，冲击荷载持续时间和实际锤击能量传递减少，如试验中可见的锤体强烈反弹。
20世纪90年代，一种利用固体燃料燃爆顶推反力配重对桩施加冲击的试桩方法Statnamic问世，反力配重的重量可按预期激发承载力的5%~10%设置，冲击荷载持续时间由DLT的10~30 ms延长至100 ms左右。不久，将DLT的落锤重量提高3~5倍，即与Statnamic反力配重相当，也得到冲击荷载持续时间延长的类似效果。因此，国际上将大幅提高锤（配）重的落锤式或燃爆式试桩方法，统称为快速载荷试验RLT，它与基于波动理论的DLT不同，采用了刚体力学简化，并以冲量形式规定了测试波形的荷载峰值不低于预期激发承载力和荷载持续时间td满足
td⩾10L/c。 (1) 式中：L为桩长；c为桩身应力波传播速度。这种基于单一td时间量的RLT有效性评价的盲目性显而易见：轻锤短持续加载，短桩整桩运动也接近刚体；重锤长持续加载，长桩桩身的波传播现象也难消除。
实现充足、无害、高效的冲击能量传递并引起桩-土系统大变形是DLT和RLT的共同目标，但大力倡导重锤低击的同时也会面临重型锤击设备移位安装难度增加、特别是与静载试验（static load test简称SLT）对标性价比下降的瓶颈。所以，与基于桩-土系统模型的传统试验设计和信号分析思路不同，本文采用能直接反映锤与桩-土系统相互作用机制的力学量（锤的动量、桩对锤的作用力冲量、能量传递效率），探究了影响锤与桩-土系统广义阻抗匹配程度的规律，其次，基于波动理论，分析了RLT因力学简化导致的原理缺陷，提出DLT与RLT相互融合的建议。
1. 锤与桩的阻抗匹配
1.1 两弹性杆撞击
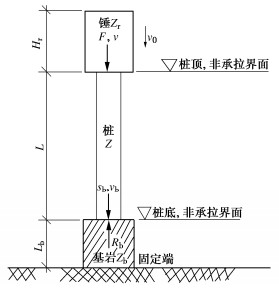
用长度为Lr的杆代表锤，阻抗为Zr，波速为cr；用长度为L的杆代表桩，阻抗为Z，波速为c。锤以初速度v0沿桩轴向对桩撞击。假设L/c≫Lr/cr，以确保在2L/c时间内的计算应力波幅值不会受起始入射波到达桩底后向桩顶撞击端反射的影响。当Zr≤Z时，撞击一次即结束，所产生的矩形力脉冲时间宽度为2Lr/cr。对于Zr＞Z，锤与桩发生多次撞击，桩身将依次出现如图 1虚线所示的多个幅值由高到低、时间宽度均为2Lr/cr的矩形力脉冲。表 1按阻抗比Zr/Z由低到高计算了6种情况的力脉冲幅值分布。
表 1 前6次撞击时的力波幅值(×Zv0)沿桩分布Table 1. Force amplitudes (×Zv0) of first six strikes along pileZr/Z F(6) F(5) F(4) F(3) F(2) F(1) 0.5 — — — — — 0.3333 1 — — — — — 0.5000 2 0.0027 0.0082 0.0247 0.0741 0.2222 0.6667 4 0.0622 0.1037 0.1728 0.2880 0.4800 0.8000 8 0.2530 0.3253 0.4182 0.5377 0.6914 0.8889 16 0.5034 0.5705 0.6465 0.7327 0.8304 0.9412 当桩很短，Lr/cr=L/c时，不论Zr/Z的比值如何，撞击都将一次结束。为便于理解，可将锤和桩想象成两个不同质量的钢球沿水平向自左向右对心撞击，撞击后将出现3种现象：① Zr＜Z，锤向左回弹，桩以小于v0的速度向右飞离，锤的动能或动量部分传递给桩；② Zr=Z，锤静止，桩恰以v0的速度向右飞离，锤的动能或动量完全传递给桩；③ Zr＞Z，锤以小于v0的速度追赶，桩以大于v0的速度向右飞离，锤的动能或动量也是部分传递给了桩。
1.2 锤作为刚体对弹性杆撞击
由表 1的趋势可见，当Zr/Z→∞时，只要桩足够长、桩身应力不受桩底反射波的影响，各次撞击的桩顶力幅值F(1)=F(2)=…=Zv0，相当于静载荷作用。基于钢材的阻抗一般比混凝土高4~5倍，可将锤近似看作刚体，则锤与桩的撞击问题变成了完全刚性的锤体对弹性杆的撞击问题。陈凡等[5]分别对刚体和桩采用牛顿第二定律和波动理论，导出关于桩身质点运动速度v的一阶微分方程：
dvdt+ρcAmrv=0， (2) 由该方程的解得到桩身撞击力F的表达式：
F=Zv=Zv0⋅exp(−ZZr⋅crLrt)=Zv0⋅exp(−mpmr⋅cLt)。 (3) 式（2），（3）中：ρ，c，A分别为桩身的质量密度、波速和横截面积；Z=ρcA，mp=ρAL分别为桩的阻抗和质量；mr为锤的质量。图 1给出了不同mp/mr比值时的桩顶冲击力曲线，且默认锤的动能和动量无损失传递。由式（3）可见，锤与桩的阻抗比或质量比大小与撞击力冲量成正比。当Zr/Z→∞或mr/mp→∞时，桩顶力值不随时间变化，恒为Zv0，相当于静载作用，与表 1趋势一致。如果假定锤和桩的材质相同，取作为锤的弹性杆长度Lr=L/8，对于Zr/Z =4，换算可得mr=0.5mp，取表 1与Zr/Z=4对应行的6次撞击力阶跃的数据并用虚线绘于图 1。如此比较可知：只要桩与锤的质量比mp/mr一定，不论锤是Zr/Z≥1的弹性杆还是刚体，锤与桩撞击产生的力冲量相等。
由于不存在桩周岩土阻力和桩底产生的反射波，桩身的速度波幅值恒满足v≡F/Z，故锤-桩匹配对冲量影响的规律，也同样适合撞击能量的传递。但必须重申，对于锤与桩阻抗不匹配（Zr/Z＜1）的情况，锤的动量或动能传递效率一定低于100%。
2. 锤与桩-土系统相互作用时的动量和能量传递
2.1 冲量
正如SLT反力配重不足则无法测定桩的极限承载力，动载试验更关注高强度荷载的持续时间长短，因为桩周岩土阻力发挥产生的反射压力波强弱与冲量正相关。只要锤体mr运动如刚体，桩顶力可直接测量或在接近桩顶的桩身采用应变计间接测量，由图 2，在锤与桩顶接触压力F＞0的时间段td，冲量积分可通过动量定理与锤的运动状态变化建立联系：
mr⋅Δvr=∫tdt0F⋅dt。 (4) 式中，t0为锤以初速v0对桩撞击的时刻；Δvr为锤体的速度改变量，其值等于vend -v0。式（4）表明：作用于锤体mr上的力冲量是锤与桩-土系统相互作用的结果，对于有“土”参与的复杂锤-桩-土系统，因式（4）计算不涉及组成并影响系统力学行为的各物体材料本构关系，故具有直接定量的优点。例如，可对基于实测桩身应变的换算力值误差予以校正；试验准备阶段若能根据冲击荷载的峰值和持续时间要求可靠地估算冲量，则按vend=0可直接获知最大的锤重或锤落距。
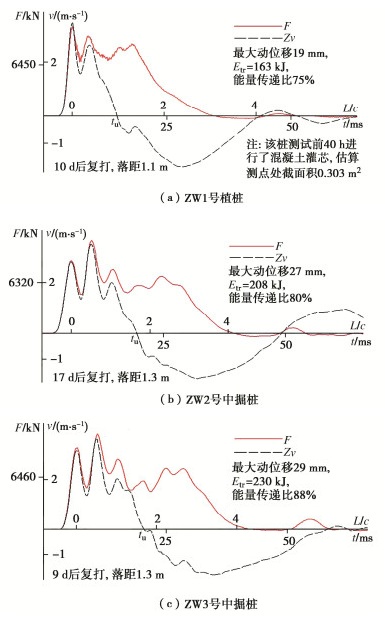
由式（4），td时段发生初次撞击，冲量积分值的大小是锤与桩-土系统相互作用效果的度量。除了荷载持续时间极长的静态情况，td时段后，锤将与桩顶脱离接触，在锤对桩二次追赶撞击发生前，锤和桩-土体系分属两个力学系统。初次撞击相互作用愈强，后期脱离表现愈烈。典型的波形表现见图 2（a），（b），图中有关试桩的勘察、设计、施工等资料见表 2。
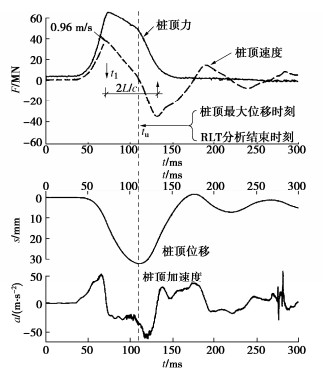
表 2 桩的勘察、设计、施工及试验资料Table 2. Geotechnical conditions and pile details图 2（a）是动力试桩常见的波形类型。桩顶位移随时间增大至时刻tu达到最大，以后沿桩身自上而下出现桩周岩土阻力卸载、桩反弹，卸载阻力通过桩对锤产生向上冲顶，锤与桩顶接触压力逐渐下降并于td时刻降至零，此刻的桩顶速度vend即为锤最终脱离桩顶回跳的初速度。在波动力学意义上，冲顶作用的强弱是桩-土系统抗压刚度或广义阻抗大小的表现，桩-土系统完全刚性时，vend = -v0。按vend =-0.83 m/s计算的锤回跳高度为3.5 cm，锤回落对桩的二次撞击显然超出信号的记录时长。
与图 2（a）不同，图 2（b）这类波形在基桩质量验收动测中虽不多见，但查找承载力低下的非正常桩本应是动测抽检的真正初衷。例如桩长较短且端阻不足，桩端反射拉力波陆续传至桩顶，引起锤与桩顶接触压力快速降低并于td时刻发生短暂溜桩现象：桩比锤下沉速度快、冲量增量为零。因为td时刻vend＞0，锤的动量改变量mr·∆vr减小，溜桩时段桩顶沉降出现二次跳跃增加，直至桩顶沉降停止或轻微反弹，锤与桩发生二次撞击，溜桩结束。仔细观察图 2（b）中的速度曲线，若采用理论基础同为波动方程的低应变反射波法判读，则无法解释反射峰宽度T2大于入射峰宽度T1的问题[5]；而依据锤与桩-土系统相互作用所涉及的广义阻抗匹配概念则能做出合理解释（下文将利用简化模型的理论计算予以证明）。在桩-土条件不变的情况下，随着锤重增加，溜桩的时长和沉降增加，整桩的运动趋于刚体，桩短时信号特征虽容易符合式（1）之于RLT的要求，但桩-土体系已为与锤无关的独立力学系统。如此，RLT视整桩为刚体，通过整桩惯性力修正，将实测的冲击激励与响应转换成准静态的桩顶荷载-沉降曲线。这种做法看似简便直观，但实际效果有违力学常理，因为至少在临近发生溜桩前，修正后的桩顶荷载为拉力，而沉降却是增大的。究其原因，溜桩时的桩体运动与理想化的两等长弹性杆撞击不同，被撞击的小阻抗杆以恒速（加速度为零）整体飞离，而实际的桩多少受到桩周土影响，加速度递减。为便于冲量直观比较，本文所有DLT实例的桩径均为800 mm，涵盖了不同的锤重、桩型和桩的承载性状，测试波形图的力和时间坐标刻度相同。
2.2 实际传递能量
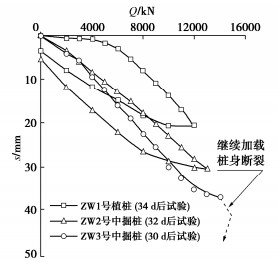
充足、无害、高效的冲击能量传递更是动载试验有效性的体现。“充足”与“无害、高效”的合理制衡就是重锤低击原则的核心。但是，如何根据实际传递给桩的能量追溯试验的有效性以及成果分析的合理性却鲜有研究[6]。动测承载力的可靠性普遍采用静动对比试验验证：对于DLT，采用信号拟合计算承载力并根据已建桩-土系统力学模型反推桩的静荷载-沉降曲线；对于RLT，采用卸荷点法UPM，根据桩顶出现最大动位移时刻tu对应的荷载和加速度，计算承载力并按预设的双曲线线型拟合出静荷载-沉降曲线[4]。由图 3的2条静载试验Q-s曲线可见：曲线1表现出承载力高、沉降s小，曲线2承载力低、沉降s大。
静载Q作用下桩顶达到最大沉降smax时，由
Emax ,s=∫0smax (5) 计算的桩-土系统吸收能量Emax, s以曲线2为大。相较于动载，静荷试验持荷时间极长，习惯上也不关注式（5）的能量值高低，因为Q-s曲线已直观反映了桩身抗压刚度和桩周岩土阻力的承载性状；对于动载试验，当缺乏静载试验对比时，桩-土系统建模及其参数的合理性只能凭实测和计算波形的拟合程度人为确认，再无任何量化的力学指标控制。因此，除桩底持力层抗压刚度大于桩身抗压刚度的端承型桩外，可利用经信号拟合确认的桩-土系统模型和最大位移，模拟桩的静载Q-s曲线并按式（5）计算Emax, s，然后用式（6）评价桩-土系统数值建模的合理性和高估承载力的危险性：
{E_{\max ,{\text{s}}}} \leqslant {E_{{\text{tr}}}} = \int_0^{{t_{\text{u}}}} F \cdot v \cdot {\text{d}}t = {C_{\text{r}}} \cdot {E_{\text{k}}}。 (6) 式中：Etr为桩实际获得的冲击能量，可理解为桩顶冲击力克服打桩阻力所做的功；Ek为锤的冲击动能；Cr为能量传递比，其值等于Etr/Ek。可惜，式（6）不是等式，因为打桩阻力既包含了与位移相关的静阻力，也包含了与变形速率相关的动阻力。不论是DLT还是RLT，激励和速度响应的幅值差别不会很大，但它们对时间的积分——冲量和位移的差别较大。运动速度幅值不变而位移增大，将使位移相关的静阻力在打桩阻力中所占的份额增大。这不仅解释了用于动阻力修正的经验阻尼系数以及计算承载力的数值有时会出现很大变异的原因，也预示着分别在静、动条件下，能量吸收Emax, s与Etr的差异随着DLT向RLT锤重增加的良性过渡而减小。
2.3 案例分析
（1）PHC800AB130（混凝土强度等级C105）管桩静动对比试验。场地代表性的地层结构为：杂填土厚约2.5 m，粉质黏土、黏质粉土层厚3.0 m，淤泥质黏土层厚9.7 m，细砂层厚1.7 m，圆砾层夹1.5 m厚粉质黏土厚12.2 m，桩端持力层为强—中风化泥质粉砂岩，其中强风化岩层厚0.8 m、中风化岩层厚度未揭穿。ZW1号桩桩长=13(下节)+15(中节)+12(上节)=39 m，采用植入法施工，旋挖成孔直径1000 mm，孔深39 m；水下灌注细石混凝土，高度约25 m。下节桩和中节桩在桩锤和管桩自重作用下自行下沉23 m深度，然后用20 t液压锤沉桩至孔底标高，此间锤的落距由0.2 m逐渐增至0.8 m。植桩后，管桩内腔混凝土芯上升高度为23 m，桩外壁包裹混凝土自孔底向上包裹深度为29 m，说明管桩内腔及外壁的混凝土均未能上返至孔口，锤击沉桩时桩周外包裹混凝土对桩中、下部土层有挤密作用，当然也伴有混凝土包裹范围的桩身阻抗增加。ZW2号和ZW3号桩采用中掘法施工，桩长37 m。锤击沉桩入土深度25 m后引孔至36.5 m。因直径400 mm长螺旋钻排土量较小，ZW2号和ZW3号桩的最终入土深度分别为34.5 m和36.7 m。由图 4（a），（b），（c）比较可见：ZW1号植桩由于广义阻抗高，能量传递比相较中掘桩略低，荷载持续时间与ZW3号中掘桩的37.2 ms相比缩短至30.1 ms。
3根管桩的静载试验曲线见图 5。对Q-s曲线用式（5）计算分级施加的静荷载累计做功Emax, s依次为176，208，264 kJ，与对应动测桩号的实测锤击能量Etr传递163，208，230 kJ相比，动测锤击能量因需额外克服岩土动阻力理应略高些才合理，但静载试桩休止时间更长会使桩周土阻力恢复（增长）。故结合动测能量的略感不足、静载试桩承载力因休止增长所造成的沉降减小两方面原因，认为DLT的实测Etr与静载Q-s曲线积分Emax, s匹配是合理的。
值得一提，图 4动测波形并不适合采用长持续RLT的UPM法计算，因为td明显偏短、桩身波传播效应显著；但按短持续DLT信号拟合预示的荷载-沉降特性也与后期的静载试验曲线呈现良好的一致性[6]。这从另一个侧面说明，可靠的动测承载力预示，首先要保证信号中的土阻力发挥信息充分。
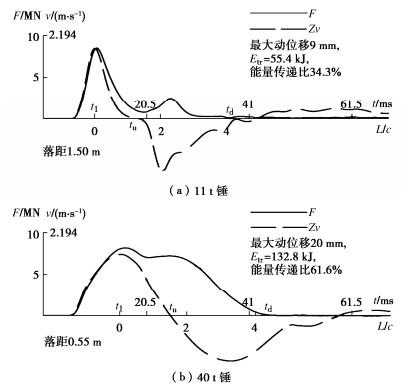
（2）1根直径800 mm、长度24.7 m的嵌岩灌注桩，先采用11 t锤锤击，停3 h后换用40 t锤锤击。该桩设计承载力特征值4500 kN，附近勘察钻孔的描述为：12.1 m厚淤泥、淤泥质土，4.5 m厚松散粉砂，3.2 m厚残积粉质黏土，3.5 m厚强风化泥质粉砂岩，桩端持力层为中—微风化泥质粉砂岩。锤击力通过加固桩头侧表面的实测应变换算得到。由图 6（a），（b）对比清晰可见，锤重增加明显改善了锤的动量和动能传递效果，增大了桩-土系统的变形。将图 4（b），（c）与图 6（b）比较还可发现：两种同为800 mm直径的桩型皆具有较高承载力，但管桩截面阻抗比灌注桩低近1倍，故20 t液压锤表现出比40 t锤更佳的匹配效果。这说明桩的承载力高低并非是影响锤与桩-土系统匹配效果的主导因素，还明显受桩身力学阻抗的影响。此外，图 6（a）波形虽用锤较轻，但仍见较强的端阻（包括嵌岩段侧阻）反射和桩对锤的冲顶作用。
![]()
图 6 不同锤重时的桩顶力和速度波形Figure 6. Records of force and velocity of pile top with different drop mass weights3. 锤与桩-土系统相互作用的模型验证
3.1 侧阻影响──基于桩底完全透射的简单情况
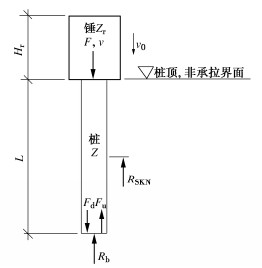
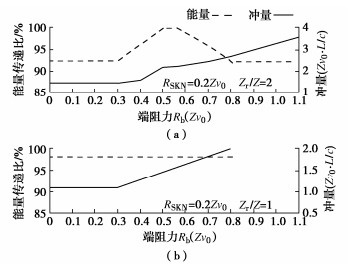
图 7是针对锤-桩-土系统采用波动力学模拟验证的简化模型，图中的符号意义同前。为计算方便，设L/c=Hr/cr，桩端反射力波Fu幅值恒为零，由桩端阻力Rb≡Fd+Fu可知，Rb恒等于桩端入射力波幅值Fd，相当于桩阻抗与持力层阻抗匹配（Z=Zb）的“全透射”情况，或理解为桩长延伸为“半无限长”。于是，可仅通过改变桩侧阻力RSKN大小，按锤与桩的阻抗比Zr/Z分别等于2，1，0.5三种条件，计算得到不同侧阻对撞击能量传递和冲量的影响趋势见图 8。由前述两自由弹性杆碰撞问题的讨论，如Zr/Z=1时，撞击一次完成，撞击力幅值为0.5Zv0。针对常见的动测桩情况，Zr/Z≥2可认为满足长持续RLT的锤重选择条件，锤对桩发生多次撞击；而Zr/Z＜0.5属于短持续DLT，撞击历时仅为2Hr/cr，且伴有锤反弹。需要补充说明：
![]()
图 8 桩侧阻对能量传递和冲量的影响Figure 8. Influences of pile skin friction on energy transfer and impulse（1）图 8中的冲量和能量曲线是在桩侧阻力RSKN发挥为恒定值的假定下计算得到的，且与位移无关，但因Zr/Z=2时将出现多次撞击，图 8（a）图也用虚线在冲量曲线下方绘出了RSKN为非恒定值发挥（发挥值随各次撞击的入射波幅值降低而递减）时的冲量曲线。
（2）图 8桩底阻抗匹配（无桩底反射）假设实际代表了桩端阻力Rb恒等于该作用界面的入射波Fd，故图 8的中间图右侧虚线和实线分别描绘了能量传递比和冲量随总阻力（RSKN+Rb）变化的趋势。
3.2 端阻影响
（1）锤-桩-端阻相互作用的波动力学计算结果见图 9。计算模型仍采用图 7，端阻Rb（包括后面计算中出现的侧阻RSKN）发挥仍假设为恒定值，但与前不同，因存在端阻或侧阻反射，计算Rb和RSKN发挥过程有时需近似迭代：例如RSKN不可能大于通过该作用截面的入射或反射波强度的2倍，上行压力波引起侧阻力反向等。下面按阻抗比Zr/Z的不同分述如下。
![]()
图 9 端阻对能量传递和冲量的影响Figure 9. Influence of toe resistance on energy transfer and impulsea）Zr/Z=2，分3种情况：①在Rb=Fd临界点左侧，即端阻Rb＜Fd、桩端反射拉力波时，将出现桩比锤下沉速度更快的溜桩现象，锤击能量不能完全传递。不过随Rb增大接近临界点时，桩端反射拉力波幅值衰减，桩的下沉速度趋缓，于是桩被向下运动速度相对快的重锤实施多次后继追赶撞击，导致临界点左侧的过渡区出现Cr快速升至100%，冲量明显增加；Rb进一步增加靠近临界点，各次追赶撞击时的撞击力幅值虽较过渡区段有所增大，但锤的撞击速度衰减加快，呈现出Cr和冲量维持短暂稳定直至Rb增大到临界点。②临界点后，初次撞击的端阻反射变为压力波，桩表现出反弹趋势，并与仍具有向下运动倾向的锤发生后继互碰，此条件下Cr尚能维持较高水平，冲量也随之增加。③随着Rb进一步增大，桩反弹渐强，锤的下冲运动状态在多次互碰过程中朝着反弹状态加速改变，此时桩对锤产生冲顶，并伴随能量传递下降；图 9（a）中右侧第二个临界点代表锤和桩以相同的速度反弹；Rb超过该点，冲顶加剧使冲量增加的同时，也终将使锤获得更大的反弹速度脱离桩顶。
b）Zr/Z=1，一次撞击即实现了能量100%传递，故Cr不随端阻Rb的增加而下降。锤与桩的运动状态有两种表现：①在桩端Rb小于临界点的溜桩段，表现为一次撞击后锤静止、桩持续下沉，特别当Rb增至临界点时，撞击后锤和桩恰好都处于静止状态。既然撞击后锤静止、桩下沉或静止，说明冲量将维持低限值不变。②Rb超过临界点后继续增加，初次撞击后锤出现短暂静止，强端阻反射也同时到达桩顶，发生桩对锤的向上冲顶，锤的动量变化增加。特别当桩端Zb→∞时，锤被桩冲顶后的回跳速度等于-v0。
c）Zr/Z=0.5，分3种情况：①Rb低于或达到临界点时，撞击后锤回跳、桩下沉，或锤回跳、桩恰好静止。②Rb超过临界点至0.5Zv0段并未引起冲量增加，原因是桩虽有反弹，但反弹速度比锤慢。③Rb超过0.5Zv0后进一步增加，强端阻反射加剧了桩的反弹，一旦反弹速度超过了锤的回跳速度，即发生桩对锤的冲顶，冲量增加。
（2）考虑较弱侧阻RSKN存在时Rb变化对锤-桩-土相互作用的影响见图 10。与图 9相比，锤的能量和动量传递规律一样，只是Zr/Z=2时，由于侧阻RSKN的存在，减缓了溜桩造成的Cr下降；对于Zr/Z=1，能量传递不受端阻变化的影响，只是RSKN的存在使Cr略微降低。
![]()
图 10 有侧阻时端阻对能量传递和冲量的影响Figure 10. Influences of toe resistance on energy transfer and impulse with skin friction需要说明，实际的锤-桩-土系统并非图 7的简化模型，也不存在L/c=Hr/cr的巧合，故Etr和冲量通常会受端阻影响，不过因侧阻先于端阻被激发，在侧阻和端阻幅值相等的条件下，侧阻对降低Cr的作用一定大于端阻。回顾图 2（a）的特例可以发现，当锤偏轻、桩较长、桩侧阻力卸载明显提前时，桩端反射（桩端微弱的拉力波和卸载强度较高的侧阻压力波叠加）到达桩顶的时刻滞后于能量传递达到最大的截止时刻tu，因此不会引起Cr降低。又因为桩端反射出现在td之后，锤已跳离桩顶且与桩分属两个力学系统，自然不会引起冲量增加。反观图 4，6（b），桩端包括桩端附近桩侧的总体压力波反射使桩对锤产生冲顶，提高了冲量并使荷载持续时间td延长。
（3）图 11是嵌岩端承桩的简化模型。模型的力学和几何参数如下：对于桩，设L=20 m，A=0.7854 m2，E=39200 N/mm2，c=4000 m/s，桩身抗压刚度Kp=EA/L。对于持力层，设层厚Lb=10 m，且在整个Lb范围内支撑面积Ab恒定，持力层弹模Eb、波速cb分别按E和c取值，持力层的阻抗Zb=EAb/c，抗压刚度Kb=EAb/Lb，于是持力层与桩的阻抗比和刚度比可简化为Ab/A。对于锤，设锤高Hr=10m，截面积为Ar，弹模Er=E，cr=c，阻抗Zr=EAr/c，锤与桩的阻抗比简化为Ar /A，当Zr /Z=0.5时，锤重约为190 kN；锤的撞击初速度v0=4 m/s，相当于落距0.816 m。
假定桩身、持力层材料的单向受压本构关系为线弹性，根据图 11模型及其参数，表 3汇总了波动力学和静力学的对比计算结果。从表中数据变化规律可见，随着桩底持力层与桩的阻抗比或刚度比增加，桩-土系统总变形能中持力层吸收能量的份额逐步下降，且静载条件下持力层吸收能量的份额低于动载，表明静载和动载输入能量相等时，静载引起的桩底位移将小于、甚至明显小于动载，锤击能量的动态传递有益于嵌岩端承桩承载能力的高效发挥。另外，由于Lb与kb成反比，Lb减小将加剧动载sb放大，反之缩小。
表 3 动载并辅以等能耗静载对比的计算结果Table 3. Calculated results: comparison between dynamic and static loads under same energy consumption阻抗比 动载 Emax, s=Etr等能耗静载对比 \frac{{{Z_{\text{b}}}}}{Z} \frac{{{Z_{\text{r}}}}}{Z} 动位移/mm Etr /kJ 最大压力/MN Cr/% 沉降/mm 桩顶静荷载Q/MN Emax, s /kJ 桩顶s 桩底 {s_{\text{b}}} 桩顶 桩底Rb 固定端 桩顶s 桩底 {s_{\text{b}}} 0.5 0.5 11.67 8.89 68.4 10.26 9.12* 13.68 88.9 13.33 6.67 10.26 68.4 1.0 16.67 13.33 153.9 15.39 13.68* 20.52 100 20.00 10.00 15.39 153.9 2.0 26.67 17.78 304.1 20.52 22.81* 27.37 98.8 27.63 13.81 22.01 304.1 1 0.5 6.67 6.67 68.4 10.26 10.26 20.52 88.9 11.55 3.85 11.85 68.4 1 10.00 10.00 153.9 15.39 15.39 30.78 100 17.32 5.77 17.78 153.9 2 19.26 13.33 307.5 20.52 27.37* 41.05 99.9 24.48 8.16 25.12 307.5 2 0.5 6.67 4.44 68.4 10.26 13.68 27.37 88.9 10.54 2.11 12.98 68.4 1 10.00 6.67 153.9 15.39 20.52 41.05 100 15.81 3.16 19.47 153.9 2 17.78 8.89 304.1 20.52 27.37 54.73 98.8 22.22 4.44 27.37 304.1 4 0.5 6.67 2.67 68.4 10.26 16.42 32.84 88.9 10.00 1.11 13.68 68.4 1 10.00 4.00 153.9 15.39 24.62 49.26 100 15.00 1.67 20.52 153.9 2 17.78 5.33 304.1 20.52 32.82 65.68 98.8 21.08 2.34 28.85 304.1 注：*表示桩底压力Rb因受固定端反射压力波的影响进一步增强。 然而，设计意图同样是端承型桩，但施工出现了异常，如桩挤土上浮，灌注桩沉渣过厚，基岩遇水软化，桩端下伏洞穴、软弱夹层、破碎带等，动测波形将呈现类似图 2（b）形态，且该图案例若按RLT施测，溜桩现象将更严重。对此，假定Zr/Z=2，桩侧阻RSKN较弱且恒定，仍按图 7简化模型来模拟端阻低下的情况：由图 12计算结果可见，随着端阻Rb减弱，2L/c时刻后的溜桩时段延长，桩顶速度和位移随之增大。采用t=0时的波动方程解析解：
{R_{\text{T}}} = \frac{1}{2}[F(t) + Zv(t)] + \frac{1}{2}\left[ {F\left( {t + \frac{{2L}}{c}} \right) - Zv\left( {t + \frac{{2L}}{c}} \right)} \right]。 (7) ![]()
图 12 不同端阻时的桩顶力和速度波形Figure 12. Waveforms of force and velocity of pile top with different toe resistances验算不同Rb时的打桩总阻力确实满足RT=RSKN+ Rb。但是，若按RLT基于刚体力学简化的静力学等效分析，溜桩段的打桩阻力与沉降的关系变得不尽合理，因为桩顶的等效静荷载为零甚至小于零。
4. 短持续DLT与长持续RLT相互融合
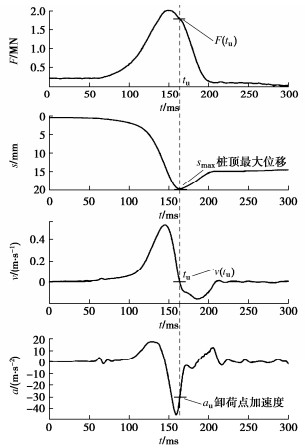
图 13为ISO试验方法标准[4]的资料性附录提供的燃爆式RLT采用UPM计算静阻力的示例。桩参数如下：L=9.78 m，A=0.132 m2，桩质量mp=3099 kg，随桩一起运动的附加土质量ma=500 kg。桩的最大静阻力（承载力）Rs, s-max按下式计算：
{R_{{\text{s,s - max}}}} = \eta \times {R_{{\text{ic}}}}({t_{\text{u}}}) = \eta \times [F({t_{\text{u}}}) - m \times {a_{\text{u}}}] = 1.77{\text{ MN}}。 (8) 式中：tu为桩顶达到最大位移smax开始卸载所对应的时刻；桩的总质量m=mp+ma=3599kg，tu时刻桩顶力F(tu)和加速度au分别为1.77 MN和–31.8 m/s2；η为与土性有关的经验系数，砂土取0.94，黏性土取0.66，本例取0.94；Ric为惯性效应修正后的桩周岩土阻力。
将式（7）做如下变形并与式（8）比较
{R_{\text{T}}} = \frac{1}{2}\left[ {F(t) + F\left( {t + \frac{{2L}}{c}} \right)} \right] - {m_{\text{p}}}\left[ {v\left( {t + \frac{{2L}}{c}} \right) - v(t)} \right]\frac{c}{{2L}}。 (9) 发现t=tu时，式（9）与式（8）中Ric计算表达的差别是：前者考虑波传播效应，桩顶的力和加速度取自tu至tu+2L/c时间段的算术平均值；后者的桩顶力和加速度按tu时刻取值，计算Ric=1.88 MN。假设c=3900 m/s，由式（7）计算RT(tu)约为1.62 MN，与Ric(tu)计算值较为接近。这可归功于RLT信号的充分有效性，图 13荷载持续时间td远超10L/c便是最好佐证。相反，若信号中土阻力发挥的信息不充分，式（7）经2L/c延时得到的RT值将更低。其实由图 13桩顶加速度或速度在tu时刻附近的变化情况便可预测，即便桩长不足10 m，桩身运动也非刚体力学的均匀状态。容易验证，当锤（配）重质量大到足以使td→∞时，桩顶的运动速度和加速度将趋于零，此时η按静态应取1，式（8）和式（9）的计算结果均等于F(tu)。作为比较，下面分析一个相对极端的案例。
马来西亚槟城二桥P25试桩[7]，全长120 m，泥面下长约113 m。桩上段35 m直径2.3 m，下段长85m，直径2.0 m。采用燃爆式RLT测试，加载设备能力按桩的工作荷载25.5MN配置，为50 MN级。地基条件（泥面下）：15 m深度范围依次为淤泥和淤泥质黏土；15~101 m为中密—密实中粗砂；101~109 m为强—中风化花岗岩；109 m以下为微风化花岗岩。
由图 14桩顶实测的力、位移、速度和加速度曲线可见，力持续时间td远未达到式（1）的要求，速度波形表现出理想嵌岩桩的反射特征。用此极端情况来刻画UPM岩土阻力Ric计算的原理缺陷很直观——未考虑tu至tu+2L/c时段桩中上部侧阻已陆续卸载、桩下部侧阻及端阻仍继续发挥所导致的全桩长范围的加速度不同向、幅值不均匀，导致按式（8）计算Ric产生“透支”。桩的动测承载力评估事关桩的正常使用与安全，业界对待原理性透支通常比较忌惮。幸好该试桩最终采用分段卸荷点法（SUPM）计算为59 MN。令人费解的是，SUPM计算需要借助事先在桩身分段埋设的传感器测量数据，使全桩长分段满足刚体力学近似。既然已预知UPM会失效，理应增加配重来减弱波传播效应，否则就失去RLT本色“倒退回”DLT了。按P25试桩mp≈1000 t，au≈-30 m/s2，由式（7）计算Ric≈80 MN，其中惯性力补偿竟达30 MN。为避免高估Ric，可借鉴式（9），尝试au取tu和tu+2L/c两个时刻的加速度算术平均值，惯性力数值可大幅降低。
另外，P25试桩虽为嵌岩桩，但根据桩顶最大位移32 mm判断，桩周激发的岩土阻力应主要源自厚度超过80 m的砂层，嵌岩段及桩端阻力尚未充分发挥，η究竟按基岩还是砂层取值很难定论，这实际和DLT的CASE法阻尼系数Jc所存在的问题类同，η原本调节“土”都有困难，还肩负着调节力学机制的责任。这对于波动力学知识和桩基工程经验欠丰富的使用者，面对相对极端的RLT，有可能因经验修正系数采信的偏执或盲目，导致桩承载力误判。
波动力学和刚体力学分别是DLT和RLT的原理基础，它们的测试波形都是锤-桩-土相互作用的力学表现。CASE法和UPM计算桩的承载力，是从打桩阻力中扣除与速度相关的动阻力、取桩顶运动速度回到零时的打桩阻力分别得到的，可见岩土经验系数修正只对与土的速率效应相关的承载力计算有意义。RLT桩身运动速度的变化率和幅值，分别明显和略微低于DLT，η经验系数修正引起的承载力变异理应比Jc小，但由式（8）的Ric项可期，“透支”程度随桩身加速度的不均匀而显著。因此，RLT可借鉴波动理论以弱化刚体力学近似带来的承载力计算不确定性。
DLT和RLT的应用都有各自适用的前提。如果前者因锤轻土阻力发挥不足而低估承载力、后者因桩身波传播现象而高估承载力，即使利用成熟的经验系数修正承载力也无意义，因为实测信号的客观性、所执行标准的约束性已无法改变。充足、无害、高效的冲击能量传递是保证动载试验充分、有效并兼顾经济性的前提，方法的理论基础完备是承载力检测结果安全可控的保障。因此，两种方法宜取长补短、相互融合，在波动理论基础下以求统一。理由很简明，波动力学可以兼容静力学或刚体力学，反之不行。
5. 结论
本文利用应力波理论并结合实例对DLT和RLT的原理进行了较深入的研究、探讨，得到以下5点结论。
（1）试验锤重选择应与桩-土系统的广义阻抗匹配，不论桩的承载力增加还是桩的截面阻抗或整桩质量增加，选配锤重均应增加。随着锤与桩的阻抗比或质量比增加，无溜桩时的锤击动能传递效率增加。
（2）锤与桩的阻抗比一定时，随着桩的总阻力增加，总体趋势是冲量增加、能量传递比下降；容易理解，总阻力一定时，摩擦型桩对能量传递比和冲量的影响大于端承型桩。
（3）总阻力与入射波强度的比值越低，或锤越重、桩的承载力尤其是端承力越低，桩底反射速度峰越宽，桩顶脱离锤体的下沉速度越快，溜桩现象越强，冲量和能量传递比都维持在较低水平。桩的承载力在溜桩发生前已发挥到极限状态，UPM法可能失效。
（4）桩对锤的冲顶强烈程度反映了总阻力的强弱。对于端承型嵌岩桩，在等能耗条件下，动载试桩的端阻力发挥效率高于SLT。
（5）当桩身波传播效应明显时，RLT的UPM承载力计算结果偏于不安全。寻求岩土经验系数来修正偏差属于治标不治本，适宜的做法还是借助波动理论，使RLT和DLT相互融合。
本文冲量公式（4）和能量公式（6）虽然形式上将RLT的式（1）与试验锤重和锤落距建立了联系，但由于桩周岩土的复杂和极强变异性，实测信号会不同程度的出现与理论广义阻抗匹配条件不符的情况。
本文研讨未考虑桩的静阻力发挥滞后于动阻力和桩端持力层为坚硬岩土层时的端阻力超前发挥问题，以及缓冲垫和替打对能耗和桩身应力水平的影响。
-
![]()
图 6 不同锤重时的桩顶力和速度波形
Figure 6. Records of force and velocity of pile top with different drop mass weights
![]()
图 8 桩侧阻对能量传递和冲量的影响
Figure 8. Influences of pile skin friction on energy transfer and impulse
![]()
图 9 端阻对能量传递和冲量的影响
Figure 9. Influence of toe resistance on energy transfer and impulse
![]()
图 10 有侧阻时端阻对能量传递和冲量的影响
Figure 10. Influences of toe resistance on energy transfer and impulse with skin friction
![]()
图 12 不同端阻时的桩顶力和速度波形
Figure 12. Waveforms of force and velocity of pile top with different toe resistances
表 1 前6次撞击时的力波幅值(×Zv0)沿桩分布
Table 1 Force amplitudes (×Zv0) of first six strikes along pile
Zr/Z F(6) F(5) F(4) F(3) F(2) F(1) 0.5 — — — — — 0.3333 1 — — — — — 0.5000 2 0.0027 0.0082 0.0247 0.0741 0.2222 0.6667 4 0.0622 0.1037 0.1728 0.2880 0.4800 0.8000 8 0.2530 0.3253 0.4182 0.5377 0.6914 0.8889 16 0.5034 0.5705 0.6465 0.7327 0.8304 0.9412 
下载: 导出CSV
表 3 动载并辅以等能耗静载对比的计算结果
Table 3 Calculated results: comparison between dynamic and static loads under same energy consumption
阻抗比 动载 Emax, s=Etr等能耗静载对比 \frac{{{Z_{\text{b}}}}}{Z} \frac{{{Z_{\text{r}}}}}{Z} 动位移/mm Etr /kJ 最大压力/MN Cr/% 沉降/mm 桩顶静荷载Q/MN Emax, s /kJ 桩顶s 桩底 {s_{\text{b}}} 桩顶 桩底Rb 固定端 桩顶s 桩底 {s_{\text{b}}} 0.5 0.5 11.67 8.89 68.4 10.26 9.12* 13.68 88.9 13.33 6.67 10.26 68.4 1.0 16.67 13.33 153.9 15.39 13.68* 20.52 100 20.00 10.00 15.39 153.9 2.0 26.67 17.78 304.1 20.52 22.81* 27.37 98.8 27.63 13.81 22.01 304.1 1 0.5 6.67 6.67 68.4 10.26 10.26 20.52 88.9 11.55 3.85 11.85 68.4 1 10.00 10.00 153.9 15.39 15.39 30.78 100 17.32 5.77 17.78 153.9 2 19.26 13.33 307.5 20.52 27.37* 41.05 99.9 24.48 8.16 25.12 307.5 2 0.5 6.67 4.44 68.4 10.26 13.68 27.37 88.9 10.54 2.11 12.98 68.4 1 10.00 6.67 153.9 15.39 20.52 41.05 100 15.81 3.16 19.47 153.9 2 17.78 8.89 304.1 20.52 27.37 54.73 98.8 22.22 4.44 27.37 304.1 4 0.5 6.67 2.67 68.4 10.26 16.42 32.84 88.9 10.00 1.11 13.68 68.4 1 10.00 4.00 153.9 15.39 24.62 49.26 100 15.00 1.67 20.52 153.9 2 17.78 5.33 304.1 20.52 32.82 65.68 98.8 21.08 2.34 28.85 304.1 注：*表示桩底压力Rb因受固定端反射压力波的影响进一步增强。
下载: 导出CSV
-
[1] RAUSCHE F, GOBLE G G, LIKINS G E Jr. Dynamic determination of pile capacity[J]. Journal of Geotechnical Engineering, 1985, 111(3): 367-383.
[2] 陈凡. FEIPWAPC特征线桩基波动分析程序[J]. 岩土工程学报, 1990, 12(5): 65-75. http://www.cgejournal.com/cn/article/id/9407 CHEN Fan. Wave analysis program of FEIPWAPC characteristic line pile foundation[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(5): 65-75. (in Chinese) http://www.cgejournal.com/cn/article/id/9407
[3] RAUSCHE F, NAGY M, LIKINS G. Mastering the art of pile testing[C]// Proceedings of the 8th International Conference on the Application of Stress-wave Theory to Piles. Lisbon, 2008: 19-32.
[4] ISO 22477—10: 2016, Geotechnical Investigation and Testing—Testing of geotechnical Structures—Part 10: Testing of piles: rapid load testing[S]. 2016.
[5] 陈凡. 基桩质量检测技术[M]. 北京: 中国建筑工业出版社, 2003. CHEN Fan. Quality Inspection Technology of Foundation Piles[M]. Beijing: China Architecture & Building Press, 2003. (in Chinese)
[6] 陈凡. 基桩动力检测理论与实践[M]. 北京: 中国建筑工业出版社, 2021. CHEN Fan. Theory and Practice of Pile Dynamic Testing[M]. Beijing: China Architecture and Building Press, 2021. (in Chinese)
[7] 王湛, 刘宇峰, 娄学谦, 等. 基于静动法的大直径超长桩承载力实测分析[J]. 地震工程学报, 2014, 36(4): 1113-1117. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201404058.htm WANG Zhan, LIU Yufeng, LOU Xue-qian, et al. Actual analysis of bearing capacity of piles with super-large diameter and deep penetration based on Statnamic method[J]. China Earthquake Engineering Journal, 2014, 36(4): 1113-1117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201404058.htm
-
期刊类型引用(0)
其他类型引用(2)
计量
- 文章访问数: 262
- HTML全文浏览量: 51
- PDF下载量: 82
- 被引次数: 2
