Consolidation behaviors of multi-reinforcement composite ground considering time- and depth-dependent clogging effects of prefabricated vertical drains
-
摘要: 以塑料排水板联合水泥搅拌桩复合地基为研究对象，假定排水板的渗透系数随时间的指数函数与深度的线性函数同时衰减，考虑了排水板淤堵的时空变化效应；同时，考虑排水板涂抹作用、水泥搅拌桩的扰动效应以及土体径、竖向渗流，建立了该问题的多元复合地基固结解析模型，推导了该模型的固结控制方程及其解析解，并将解答退化到排水板淤堵效应仅随时间变化和仅随深度变化的工况。通过将本文解答与实际工程案例进行对比分析，验证了本文解答的正确性。最后，采用参数敏感性分析法对多元复合地基固结性状进行研究。研究结果表明：相对于恒井阻的情况，考虑排水板的淤堵效应时空变化的地基平均孔压的消散和固结将减慢，且减慢的趋势可看作单一因素减慢趋势的叠加；θ1越小，θ2和θ3越大，多元复合地基固结越慢，当θ3较大时，径向固结停止，地基最终只靠竖向渗流完成固结。Abstract: Taking the composite ground improved by prefabricated vertical drains (PVDs) and cement mixing piles as the research object, an analytical model for the consolidation of multi-reinforcement composite foundation is established by considering the clogging effects of PVDs based on an assumption that their permeability coefficient decays simultaneously as an exponential function of time and a linear function of depth. Moreover, the following factors are also considered: the smearing effects of PVDs, the disturbance effects of cement mixing piles, and the radial and vertical seepages within the soil. The analytical solutions for the analytical model are subsequently deduced. After then, the solutions are degenerated to the cases with only the time- or depth-dependent well resistance. The correctness of the solutions is verified by comparing the predicted results with the measured data. Finally, the consolidation behaviors of the multi-reinforcement composite foundation are investigated through a series of the parametrical analysis. The results show the consolidation rate slows down when considering the time- and depth-dependent well resistance of PVDs by comparing that of the constant well resistance. Moreover, the reduction in the consolidation rate can be regarded as the sum of the influences of each single factor. The smaller the values of θ1 and the larger the values of θ2 and θ3, the slower the consolidation rate. When θ3 increases to a certain extent, the radial consolidation ceases, and the consolidation process will be completed only by the vertical flow at the later stage of consolidation.
-
0. 引言
多元复合地基可同时拥有多种增强体的特性，故其在道路、机场、码头等软土地基处理的工程中被广泛应用[1-3]。常见的多元复合地基处理形式有塑料排水板联合水泥搅拌桩复合地基、长板-短桩复合地基、散体材料桩联合不透水桩复合地基等。多元复合地基固结理论是预测复合地基沉降和沉降控制设计的基础，对其固结理论的研究也愈发得到学者们的重视。
多元复合地基具有地基形式多样化、边界条件复杂化、土体及增强体材料差异较大等特点，使得相关的理论研究还处于发展阶段。Zhang等[4-5]建立了将塑料排水板联合粉喷桩复合地基等效为均质土体的多元复合地基固结解析解；陈蕾等[6]建立了以排水板为中心，将粉喷桩等效为不透水环位于单元外围的多元复合地基固结的解析解和数值解；刘吉福[7]认为复合地基中的排水桩和不透水桩均存在孔压，且假定孔压随深度成比例变化；Ye等[8-9]建立以水泥搅拌桩为中心，将排水板等效为环状排水墙位于单元外围的模型，并假定土体中的水流由单元中心向外围排水墙发生渗流；Zhang等[10]同样采用排水墙的方法建立了长板-短桩复合地基固结解析解；杨涛等[11]建立了考虑碎石桩为恒井阻时在瞬时荷载作用下的碎石桩-不排水桩复合地基固结解析解；Lu等[12-13]提出3种多元复合地基模型，建立了考虑排水板为恒井阻时塑料排水板联合不透水桩复合地基固结解析解。上述研究均未考虑排水板或砂井的淤堵效应。
随着固结的发展，排水体将产生淤堵效应，已有部分学者对其展开研究。Deng等[14-15]假定排水板的井阻随时间及随时间和深度同时增大，研究了排水板单一复合地基的固结特性；郭霄等[16]基于Deng等[15]变井阻假定，推导了竖井地基等应变条件下径向固结的控制方程及解析解；江文豪等[17]同样基于Deng等[15]变井阻假定，推导了考虑土体中径-竖向渗流的砂井地基固结理论。现有关于淤堵效应的研究均以竖井地基为模型，多元复合地基固结理论均未考虑淤堵效应。
本文在现有研究的基础上，考虑排水板的淤堵效应，假定其井阻随时间和深度同时衰减，推导了该问题的固结控制方程及4种常见荷载下的解析解答，该解答同时将排水板的涂抹作用、水泥搅拌桩的扰动效应以及土体的竖向与径向渗流考虑在内。然后，通过与现场案例进行对比，验证了本文的正确性。最后，基于解析解答分析井阻效应、井阻因子、附加应力沿深度分布形式对多元复合地基的固结度及孔压的影响。
1. 计算模型
1.1 模型的建立
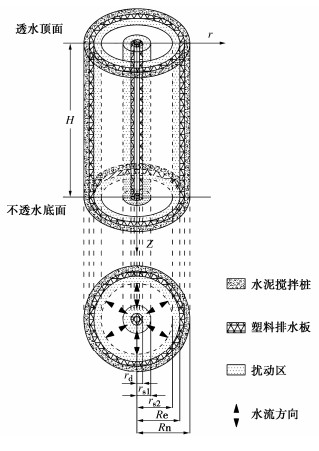
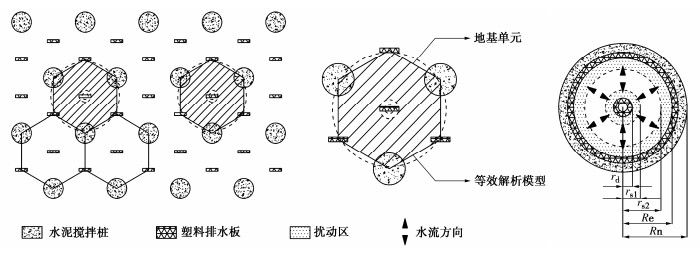
在实际工程中，多元组合桩复合地基大多以三角形、矩形等规则形式布置，模型单元可以塑料排水板或水泥搅拌桩为中心划分单元，本文以卢萌盟等[13]提出的适用于多桩型任意排列形式布置的模型C为研究对象。如图 1所示，在三角形布置方式下，以塑料排水板为中心进行单元划分，单元外围同时包含${n_{\text{d}}}$个塑料排水板和${n_{\text{p}}}$个水泥搅拌桩，按面积等效的原则，外围排水板和水泥搅拌桩的等效个数均为1个，模型单元中心及外围均有排水板，因此模型中的孔隙水沿径向同时存在向内和向外的双向渗流。图 2为复合地基等效单元的计算模型，单元中心排水板的涂抹区为半径$r$在${r_{\text{d}}}\sim{r_{{\text{s1}}}}$之间的环形影响区，该涂抹区土体的渗透系数为${k_{{\text{s1}}}}$；由单元外围的排水板引起的涂抹作用和水泥搅拌桩施工造成的扰动效应共同作用的影响区为半径$r$在${r_{{\text{s2}}}}\sim{R_e}$之间的环形影响区，该影响区土体的渗透系数为${k_{{\text{s2}}}}$；半径$r$在${r_{{\text{s1}}}}\sim{r_{{\text{s2}}}}$间为未扰动的土体，其渗透系数为${k_{\text{h}}}$。
单元中心排水板按环形等效原则[18]进行等效，即排水板的周长和面积在等效前后均保持不变的情况下，将排水板等效为环状排水体。表达式如下：
$$ {r_{\text{d}}} = \frac{{\omega + b}}{{\text{π }}}\text{，} $$ (1) $$ \omega b = \zeta {\text{π }}r_{\text{d}}^2。 $$ (2) 式中：${r_{\text{d}}}$为中心排水板的等效半径；$\omega $，$b$分别为排水板的宽度和厚度；$\zeta $为排水板的面积折减系数，通过该参数来保证等效后环形排水体的截面积与排水板的截面积相同。面积折减系数可表示为
$$ \zeta = \frac{{{\text{π }}\omega b}}{{{{(\omega + b)}^2}}}。 $$ (3) 中心排水板引起的涂抹区的半径和渗透系数与单个排水板引起的涂抹区的半径和渗透系数的值相同，即${r_{{\text{s1}}}}{\text{ = }}{r_{{\text{sd}}}}$，${k_{{\text{s1}}}}{\text{ = }}{k_{{\text{sd}}}}$。由单元外围排水板引起的涂抹作用和水泥搅拌桩施工造成的扰动效应共同作用的影响区的面积为${n_{\text{d}}}$个塑料排水板的涂抹区面积和${n_{\text{p}}}$个水泥搅拌桩扰动区的面积之和，计算式如下：
$$ {r_{{\text{s2}}}} = \sqrt {R_{\text{e}}^2 - {n_{\text{d}}}(r_{{\text{sd}}}^2 - r_{\text{d}}^2) - {n_{\text{p}}}(r_{{\text{sp}}}^2 - r_{\text{p}}^2)} 。 $$ (4) 式中：${n_{\text{d}}}$和${n_{\text{p}}}$分别为单元外围塑料排水板和水泥搅拌桩的数量；${R_{\text{e}}}$为影响区半径；${r_{\text{p}}}$为单个水泥搅拌桩的半径；${r_{{\text{s1}}}}$为单元中心排水板引起的扰动区的外半径；${r_{{\text{s2}}}}$为单元外围影响区的内半径；${r_{{\text{sd}}}}$和${r_{{\text{sp}}}}$分别为单个排水板引起的涂抹区和单个水泥搅拌桩引起的扰动区的半径。
对于外围排水板引起的涂抹作用和水泥搅拌桩施工造成的扰动效应共同作用下的渗透系数${k_{{\text{s2}}}}$，按面积的加权平均值计算，计算式如下：
$$ {k_{{\text{s2}}}} = \frac{{{n_{\text{d}}}{k_{{\text{sd}}}}(r_{{\text{sd}}}^2 - r_{\text{d}}^2) + {n_{\text{p}}}{k_{{\text{sp}}}}(r_{{\text{sp}}}^2 - r_{\text{p}}^2)}}{{{n_{\text{d}}}(r_{{\text{sd}}}^2 - r_{\text{d}}^2) + {n_{\text{p}}}(r_{{\text{sp}}}^2 - r_{\text{p}}^2)}} \text{，} $$ (5) 式中，${k_{{\text{sd}}}}$和${k_{{\text{sp}}}}$分别为单个排水板引起的涂抹区和单个水泥搅拌桩引起的扰动区的渗透系数。
由复合地基等效单元的计算模型可得，影响区半径为
$$ R_{\text{e}}^2 = \frac{{{A_{\text{n}}} - {A_{{\text{d1}}}} - {A_{{\text{p1}}}}}}{{\text{π }}} 。 $$ (6) 式中：$ {A}_{\text{n}}=\text{π}{R}_{\text{n}}^{2}；{A}_{\text{d1}}={n}_{\text{d}}\omega b；{A}_{\text{p1}}={n}_{\text{d}}\text{π}{r}_{\text{p}}^{2} $；${A_{\text{n}}}$，${A_{{\text{d1}}}}$和${A_{{\text{p1}}}}$分别为计算单元、单元外围排水板和单元外围水泥搅拌桩的面积；${R_{\text{n}}}$为计算单元的半径。
结合式（1），（2），（6）可得
$$ R_{\text{e}}^2 = R_{\text{n}}^2 - \zeta {n_{\text{d}}}r_{\text{d}}^2 - {n_{\text{p}}}r_{\text{p}}^2。 $$ (7) 1.2 基本假定
（1）土体为饱和土，土颗粒和孔隙水不可压缩，土体的变形源于孔隙水的排出。
（2）等应变条件成立，即土体、排水板和水泥搅拌桩的竖向变形相等。
（3）土体及排水板中的渗流服从达西定律。
（4）考虑排水板的淤堵效应随时间和围压的增大而增大，因此假定排水板渗透系数${k_{{\text{Dd}}}}$随时间指数衰减，且同时随深度线性衰减，即
$$ {k_{{\text{Dd}}}} = {k_0}\left( {{\theta _1} - {\theta _2}\frac{z}{H}} \right){{\text{e}}^{ - {\theta _3}t}}。 $$ (8) 式中：${k_{\text{0}}}$为塑料排水板的初始渗透系数；${\theta _1}$，${\theta _2}$，${\theta _3}$为常数，且$ {\theta }_{1}＞0 $，$0 \leqslant {\theta _2} \leqslant {\theta _1}$（为了确保渗透系数为正），${\theta _3} \geqslant 0$；${\theta _1}$和${\theta _2}$用来描述排水板排水能力随深度的变化，即井阻的深度影响因子；${\theta _3}$用来描述排水板排水能力随时间的变化，即井阻的时间影响因子。
（5）排水板满足流量连续相等假定，即沿径向流入中心排水板和外围排水板的水量等于沿竖向流出的水量。式（9）表示中心排水板流量连续相等的假定，式（10）表示单元外围排水板流量连续相等的假定，具体表达式如下；
$$ {\left. {\left[ {2{\text{π }}r\frac{{{k_{\text{r}}}(r)}}{{{\gamma _{\text{w}}}}}\frac{{\partial {u_{\text{s}}}}}{{\partial r}}} \right]} \right|_{r = {r_{\text{d}}}}} = - \frac{{\zeta {\text{π }}r_{\text{d}}^2}}{{{\gamma _{\text{w}}}}}\frac{\partial }{{\partial z}}\left( {{k_{{\text{Dd}}}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}}} \right)\text{，} $$ (9) $$ {\left. {\left[ {2{\text{π }}r\frac{{{k_{\text{r}}}(r)}}{{{\gamma _{\text{w}}}}}\frac{{\partial {u_{\text{s}}}}}{{\partial r}}} \right]} \right|_{r = {R_{\text{e}}}}} = \frac{{{n_{\text{d}}}\zeta {\text{π }}r_{\text{d}}^2}}{{{\gamma _{\text{w}}}}}\frac{\partial }{{\partial z}}\left( {{k_{{\text{Dd}}}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}}} \right) 。 $$ (10) 式中：$r$为径向坐标；${k_{\text{r}}}(r)$为桩周土体的水平渗透系数；${u_{\text{s}}}$和${u_{\text{d}}}$分别为土体和排水板内任意一点任一时刻的超静孔压；${\gamma _{\text{w}}}$为水的重度。
2. 控制方程的推导及解答
2.1 控制方程的推导
首先，中心排水板与土体界面的超孔隙水压力相等，即
$$ \left.u_{\mathrm{s}}(r, z, t)\right|_{r=r_{\mathrm{d}}}=u_{\mathrm{d}} \quad 。 $$ (11) 另外，多元复合地基的外部荷载由${n_{\text{d}}} + 1$个塑料排水板、${n_{\text{p}}}$个水泥搅拌桩和土体共同承担，即
$$ {\overline \sigma _{\text{d}}}{A_{\text{d}}} + {\overline \sigma _{\text{p}}}{A_{\text{p}}} + {\overline \sigma _{\text{s}}}{A_{\text{s}}} = \sigma {A_{\text{n}}} 。 $$ (12) 式中：$ \sigma =\sigma (z，t) $为荷载在地基内引起的附加应力；$ {\overline \sigma _{\text{d}}} $，$ {\overline \sigma _{\text{p}}} $和$ {\overline \sigma _{\text{s}}} $分别为排水板、水泥搅拌桩和土体任意深度的总平均应力；${A_{\text{d}}}$，${A_{\text{p}}}$，${A_{\text{s}}}$和${A_{\text{n}}}$分别为塑料排水板、水泥搅拌桩、土体和地基单元的截面积；${A_{\text{d}}} = \zeta ({n_{\text{d}}} + 1){\text{π }}r_{\text{d}}^2$，${A_{\text{p}}} = {n_{\text{p}}}{\text{π }}r_{\text{p}}^2$，${A_{\text{s}}} = {\text{π }}(R_{\text{e}}^2 - r_{\text{d}}^2)$，${A_{\text{n}}} = $ ${\text{π }}R_{\text{n}}^2 = {A_{\text{p}}} + {A_{\text{d}}} + {A_{\text{s}}}$。
由假设（2）可知，等应变假设可表达为
$$ \frac{{{{\overline \sigma }_{\text{d}}} - {u_{\text{d}}}}}{{{E_{\text{d}}}}} = \frac{{{{\overline \sigma }_{\text{p}}}}}{{{E_{\text{p}}}}} = \frac{{{{\overline \sigma }_{\text{s}}} - {{\overline u }_{\text{s}}}}}{{{E_{\text{s}}}}} = {\varepsilon _z} 。 $$ (13) 式中：${E_{\text{d}}}$，${E_{\text{p}}}$和${E_{\text{s}}}$分别为塑料排水板、水泥搅拌桩和土体的压缩模量，在计算中通常假定${E_{\text{d}}} = {E_{\text{s}}}$；${\varepsilon _z}$为复合地基任一深度处的竖向应变；${\overline u _{\text{s}}}$为土体沿径向的平均超静孔压，可表示为
$$ {\overline{u}}_{\text{s}}=\frac{1}{\text{π}({R}_{\text{e}}^{2}-{r}_{\text{d}}^{2})}{\displaystyle {\int }_{{r}_{\text{d}}}^{{R}_{e}}2\text{π}r{u}_{\text{s}}(r\text{，}z\text{，}t)}\text{d}r 。 $$ (14) 垂直应变率可由式（12），（13）得
$$ \frac{{\partial {\varepsilon _z}}}{{\partial t}} = \frac{1}{{{E_{{\text{com}}}}}}\left[ {\frac{{\partial \sigma }}{{\partial t}} - \frac{{\partial \overline u }}{{\partial t}}} \right] \text{，} $$ (15) 式中，${E_{{\text{com}}}}$为复合地基的复合压缩模量，$\overline u $为地基任一深度处的平均孔隙水压力。其中
$$ \begin{aligned} E_{\text {com }}= & \frac{E_{\mathrm{p}} A_{\mathrm{p}}+E_{\mathrm{d}} A_{\mathrm{d}}+E_{\mathrm{s}} A_{\mathrm{s}}}{A_{\mathrm{n}}} \\ & =\frac{n_{\mathrm{p}} N_{\mathrm{pd}}^2 Y_{\mathrm{ps}}+\zeta\left(n_{\mathrm{d}}+1\right) Y_{\mathrm{ds}}+N^2-1}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2} E_{\mathrm{s}}, \end{aligned} $$ (16) $$ \overline u = \frac{{{u_{\text{d}}}{A_{\text{d}}} + {{\bar u}_{\text{s}}}{A_{\text{s}}}}}{{{A_{\text{n}}}}} = \frac{{\zeta ({n_{\text{d}}} + 1){u_{\text{d}}} + ({N^2} - 1){{\overline u }_{\text{s}}}}}{{{N^2} + \zeta {n_{\text{d}}} + {n_{\text{p}}}N_{{\text{pd}}}^2}} \text{，} $$ (17) 其中，
$$ {N}_{\text{pd}}=\frac{{r}_{\text{p}}}{{r}_{\text{d}}}\text{，}N=\frac{{R}_{\text{e}}}{{r}_{\text{d}}}\text{，}{Y}_{\text{ps}}=\frac{{E}_{\text{p}}}{{E}_{\text{s}}}\text{，}{Y}_{\text{ds}}=\frac{{E}_{\text{d}}}{{E}_{\text{s}}} 。 $$ 参考谢康和等[19]的研究，土体的固结方程可统一写为
$$ \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {\frac{{{k_{\text{r}}}(r)}}{{{\gamma _{\text{w}}}}}r\frac{{\partial {u_{\text{s}}}}}{{\partial r}}} \right] + \frac{{{k_{\text{v}}}}}{{{\gamma _{\text{w}}}}}\frac{{{\partial ^2}{{\overline u }_{\text{s}}}}}{{\partial {z^2}}} = - \frac{{\partial {\varepsilon _z}}}{{\partial t}} \text{，} $$ (18) 式中，${k_{\text{v}}}$为土体的平均竖向渗透系数。
参考Lu等[20]研究，利用边界条件式（9）~（11）对式（18）沿径向积分，并联立式（14），（15），（17）可得关于土体中超静孔压的3个偏微分方程，即本文的求解方程：
$$ {\overline u _{\text{s}}} = {u_{\text{d}}} - \frac{{{\lambda _1}{\theta _2}{k_{\text{0}}}}}{{{\lambda _4}}}{{\text{e}}^{ - {\theta _3}t}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}} + \frac{{{\lambda _1}}}{{{\lambda _4}}}{k_{{\text{Dd}}}}\frac{{{\partial ^2}{u_{\text{d}}}}}{{\partial {z^2}}} \text{，} $$ (19) $$ \overline u = {\lambda _8}{u_{\text{d}}} + {\lambda _7}{{\text{e}}^{ - {\theta _3}t}}\frac{{\partial {u_{\text{d}}}}}{{\partial z}} + {\lambda _3}{k_{{\text{Dd}}}}\frac{{{\partial ^2}{u_{\text{d}}}}}{{\partial {z^2}}} \text{，} $$ (20) $$ \begin{gathered} \lambda_1 k_{\mathrm{Dd}} \frac{\partial^4 u_{\mathrm{d}}}{\partial z^4}+\lambda_2 \mathrm{e}^{-\theta_3 t} \frac{\partial^3 u_{\mathrm{d}}}{\partial z^3}+\lambda_3 k_{\mathrm{Dd}} \frac{\partial^3 u_{\mathrm{d}}}{\partial z^2 \partial t}+\lambda_7 \frac{\partial^2 u_{\mathrm{d}}}{\partial z \partial t}+\lambda_8 \frac{\partial u_{\mathrm{d}}}{\partial t}+ \\ \left(\lambda_4+\lambda_5 \mathrm{e}^{-\theta_3 t}+\lambda_6 k_{\mathrm{Dd}}\right) \frac{\partial^2 u_{\mathrm{d}}}{\partial z^2}-\lambda_7 \theta_3 \mathrm{e}^{-\theta_3 t} \frac{\partial u_{\mathrm{d}}}{\partial z}=\frac{\partial \sigma}{\partial t} 。\;\;\;\;\;\;\;\;\;\;\;\;\;\; \end{gathered} $$ (21) 其中，
$$ \begin{array}{ll} \lambda_1=-\frac{k_{\mathrm{v}} F_{\mathrm{c}} E_{\mathrm{com}}}{\gamma_{\mathrm{w}}\left(N^2-1\right)}, & \lambda_2=-\frac{3 \theta_2 k_0 k_{\mathrm{v}} F_{\mathrm{c}} E_{\mathrm{com}}}{H \gamma_{\mathrm{w}}\left(N^2-1\right)}, \\ \lambda_3=\frac{F_{\mathrm{c}}}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2}, & \lambda_4=-\frac{k_{\mathrm{v}} E_{\mathrm{com}}}{\gamma_{\mathrm{w}}}, \\ \lambda_5=-\frac{\theta_3 k_0 E_{\mathrm{com}} \zeta\left(1-n_{\mathrm{d}}\right)}{H \gamma_{\mathrm{w}}\left(N^2-1\right)}, & \lambda_6=\lambda_3 \theta_3-\frac{\zeta E_{\mathrm{com}}\left(1-n_{\mathrm{d}}\right)}{\gamma_{\mathrm{w}}\left(N^2+1\right)}, \\ \lambda_7=-\frac{\theta_2 k_0 F_{\mathrm{c}}}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2}, & \lambda_8=\frac{\zeta\left(n_{\mathrm{d}}+1\right)+N^2+1}{N^2+\zeta n_{\mathrm{d}}+n_{\mathrm{p}} N_{\mathrm{pd}}^2} 。 \end{array} $$ 式中，$ {F_{\text{c}}} $表达式的推导参考文献[13]。
2.2 控制方程的解答
假定复合地基顶部透水（孔压为零），底部不透水（流速为零），故竖向边界条件可以写为
$$ \left.\begin{array}{l} \left.\bar{u}(z, t)\right|_{z=0}=0,\left.\quad u_{\mathrm{d}}(z, t)\right|_{z=0}=0, \\ \left.\frac{\partial \bar{u}(z, t)}{\partial z}\right|_{z=H}=0,\left.\quad \frac{\partial u_{\mathrm{d}}(z, t)}{\partial z}\right|_{z=H}=0 。 \end{array}\right\} $$ (22) 在初始时刻，外部荷载由复合地基的平均孔压承担，则初始条件为
$$ \left.\bar{u}(z, t)\right|_{t=0}=\sigma(z, 0)=\sigma_0 \quad, $$ (23) 式中，$ {\sigma _0} $为初始附加应力。
本文采用分离变量法对非齐次方程式（21）进行求解，假设其解为
$$ {u_{\text{d}}}(z,t) = \sum\limits_{m = 1}^\infty {{T_m}(t)\sin \left( {\frac{M}{H}z} \right)} \text{，} $$ (24) 其中，
$$ M = \frac{{2m - 1}}{2}{\text{π }}\;\;\;\;\;\;\;\;\;\;\;\;(m = 1,2,3, \cdot \cdot \cdot ) 。 $$ 将式（24）代入式（21），然后在式两边同时乘以$ \sin (Mz/H) $，并在[0，H]上对$z$进行积分，同时利用傅里叶级数的正交性得
$$ {T_m}^\prime (t) + {G_m}(t){T_m}(t) = {Q_m}(t) \text{，} $$ (25) 其中，
$$ {G_m}(t) = \frac{{{L_m}{{\text{e}}^{ - {\theta _3}t}} - {\lambda _4}{{\left( {\frac{M}{H}} \right)}^2}}}{{\frac{{{\lambda _7}}}{H} + {\lambda _8} - {\lambda _3}{K_m}{{\text{e}}^{ - {\theta _3}t}}}} \text{，} $$ (26) $$ {Q}_{m}(t)=\frac{\frac{2}{H}{\displaystyle {\int }_{0}^{H}\frac{\partial \sigma (z\text{，}t)}{\partial t}}\mathrm{sin}\left(\frac{M}{H}z\right)\text{d}z}{\frac{{\lambda }_{7}}{H}+{\lambda }_{8}-{\lambda }_{3}{K}_{m}{\text{e}}^{-{\theta }_{3}t}} \text{，} $$ (27) 其中，
$$ \begin{gathered} K_m=k_0\left(\theta_1-\frac{\theta_2}{2}\right)\left(\frac{M}{H}\right)^2, \\ L_m=\left[\lambda_1\left(\frac{M}{H}\right)^2-\lambda_6\right] K_m-\left(\frac{\lambda_2}{H}+\lambda_5\right)\left(\frac{M}{H}\right)^2-\frac{\lambda_7 \theta_3}{H} 。 \end{gathered} $$ 将式（24）代入式（20），然后式两边同乘以$ \sin (Mz/H) $，并在[0，H]上对$z$进行积分，结合初始条件式（23），利用傅里叶级数的正交性得
$$ {T}_{m}(0)=\frac{\frac{2}{H}{\displaystyle {\int }_{0}^{H}\sigma (z\text{，}0)\mathrm{sin}\left(\frac{M}{H}z\right)\text{d}z}}{\frac{{\lambda }_{7}}{H}+{\lambda }_{8}-{\lambda }_{3}{K}_{m}} 。 $$ (28) 结合$ {T_m}(0) $的值，由常微分方程理论得式（25）的解为
$$ {T_m}(t) = \frac{{\left[ {{P_m} + {S_m}(t)} \right]{{\text{e}}^{{\beta _m}t}}}}{{{{\left( {\frac{{{\lambda _7}}}{H} + {\lambda _8} - {\lambda _3}{K_m}{{\text{e}}^{ - {\theta _3}t}}} \right)}^{{\gamma _m}}}}} \text{，} $$ (29) 其中，
$$ {\beta _m} = \frac{{{\lambda _4}}}{{\frac{{{\lambda _7}}}{H} + {\lambda _8}}}{\left( {\frac{M}{H}} \right)^2} \text{，} $$ (30) $$ {\gamma _m} = \frac{{{L_m}}}{{{\lambda _3}{\theta _3}{K_m}}} - \frac{{{\beta _m}}}{{{\lambda _3}}} \text{，} $$ (31) $$ {P}_{m}=\frac{2{\displaystyle {\int }_{0}^{H}\sigma }(z\text{，}0)\mathrm{sin}\left(\frac{M}{H}z\right)\text{d}z}{H{\left(\frac{{\lambda }_{7}}{H}+{\lambda }_{8}-{\lambda }_{3}{K}_{m}\right)}^{1-{\gamma }_{m}}} \text{，} $$ (32) $$ \begin{aligned} S_m(t)= & \frac{2}{H} \int_0^t\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 \tau}\right) \mathrm{e}-\beta_m \tau . \\ & \int_0^H \frac{\partial \sigma(z, \tau)}{\partial \tau} \sin \left(\frac{M}{H} z\right) \mathrm{d} z \mathrm{~d} \tau \end{aligned} $$ (33) 结合式（19），（20），（24），（29）可得任意荷载作用下任一深度处排水板内的超静孔压、土体的平均超静孔压、复合地基的平均超静孔压以及复合地基总平均固结度如下（其中复合地基总平均固结度按应力定义计算）：
$$ {u_{\text{d}}} = \sum\limits_{m = 1}^\infty {\left\{ {\frac{{\left[ {{P_m} + {S_m}{\text{(}}t{\text{)}}} \right]{{\text{e}}^{{\beta _m}t}}\sin \left( {\frac{M}{H}z} \right)}}{{{{\left( {\frac{{{\lambda _7}}}{H} + {\lambda _8} - {\lambda _3}{K_m}{{\text{e}}^{ - {\theta _3}t}}} \right)}^{{\gamma _m}}}}}} \right\}} \text{，} $$ (34) $$ \begin{aligned} & \bar{u}_{\mathrm{s}}=\sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} .\right. \\ & \left.\left[\sin \left(\frac{M}{H} z\right)-\frac{\lambda_1 \theta_2 k_0}{\lambda_4} \mathrm{e}^{-\theta_3 t} \cos \left(\frac{M}{H} z\right)-\frac{\lambda_1}{\lambda_4} k_{\mathrm{Dd}} \sin \left(\frac{M}{H} z\right)\right]\right\}, \end{aligned} $$ (35) $$ \begin{aligned} & \bar{u}=\sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} .\right. \\ & \left.\left[\lambda_8 \sin \left(\frac{M}{H} z\right)+\lambda_7 \frac{M}{H} \mathrm{e}^{-\theta_3 t} \cos \left(\frac{M}{H} z\right)-\lambda_5\left(\frac{M}{H}\right)^2 k_{\mathrm{Dd}} \sin \left(\frac{M}{H} z\right)\right]\right\}, \end{aligned} $$ (36) $$ \begin{gathered} U(t)=\frac{\int_0^H[\sigma(z, t)-\bar{u}(z, t)] \mathrm{d} z}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z}=\frac{\int_0^H \sigma(z, t) \mathrm{d} z}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z}- \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \frac{1}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z} \sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} \cdot\right. \\ \left.\left\{\lambda_8 \frac{H}{M}-\lambda_5 k_0 \theta_1 \frac{M}{H}-(1)^m\left[\lambda_7 \frac{M}{H} \mathrm{e}^{-\theta_3 t}+\lambda_5 \frac{k_0 \theta_1}{H}\left(\frac{M}{H}\right)^2\right]\right\}\right\} 。 \end{gathered} $$ (37) 瞬时荷载、线性荷载、多级瞬时荷载和多级线性荷载4种常见荷载形式下解答的推导参考文献[18]，其中$ {\beta _m} $按式（30）计算。
2.3 解答的验证
通过对解答进行退化研究，从理论方面验证本文解答的有效性。
（1）当${\theta _3}{\text{ = }}0$时，本文关于复合地基任意荷载下的总平均固结度的表达式（37）可退化为考虑排水板的井阻仅随深度变化时任意荷载作用下的总平均固结度的解答，即
$$ \begin{gathered} U(t)=\frac{{\displaystyle {\int }_{0}^{H}\left[\sigma (z，t)-\overline{u}(z，t)\right]\text{d}z}}{{\displaystyle {\int }_{0}^{H}{\sigma }_{\text{u}}(z)\text{d}z}}=\frac{{\displaystyle {\int }_{0}^{H}\sigma (z，t)\text{d}z}}{{\displaystyle {\int }_{0}^{H}{\sigma }_{\text{u}}(z)\text{d}z}}-\;\;\;\;\;\;\\ \frac{1}{\int_0^H \sigma_{\mathrm{u}}(z) \mathrm{d} z} \sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m\right)^{\gamma_m}} \cdot\right. \\ \left.\left\{\lambda_8 \frac{H}{M}-\lambda_5 k_0 \theta_1 \frac{M}{H}-(-1)^m\left[\lambda_7 \frac{M}{H}+\lambda_5 \frac{k_0 \theta_1}{H}\left(\frac{M}{H}\right)^2\right]\right\}\right\} 。 \end{gathered} $$ (38) （2）当${\theta _1} = 1$，${\theta _2} \to 0$，$ \sigma (z，t)={\sigma }_{\text{u}}g(t) $时，式（37）可退化为白垚等[21]考虑排水板井阻仅随时间变化情况时任意荷载作用下多元复合地基的总平均固结度的解答，即
$$ \begin{aligned} & U(t)=g(t)-\sum\limits_{m=1}^{\infty}\left\{\frac{\left[P_m+S_m(t)\right] \mathrm{e}^{\beta_m t}}{\sigma_{\mathrm{u}}\left(\frac{\lambda_7}{H}+\lambda_8-\lambda_3 K_m \mathrm{e}^{-\theta_3 t}\right)^{\gamma_m}} .\right. \\ & \left.\left\{\lambda_8 \frac{H}{M}-\lambda_5 k_0 \frac{M}{H}-(-1)^m\left[\lambda_7 \frac{M}{H} \mathrm{e}^{-\theta_3 t}+\lambda_5 \frac{k_0}{H}\left(\frac{M}{H}\right)^2\right]\right\}\right\} . \end{aligned} $$ (39) （3）继续令${\theta _3} \to 0$，式（39）可退化为考虑排水板为恒井阻时任意荷载作用下的多元复合地基的总平均固结度的解答[13]，即
$$ U(t) = g(t) - \sum\limits_{m = 1}^\infty {\frac{2}{{{M^2}}}} \left[ {\frac{{{\sigma _0}}}{{{\sigma _{\text{u}}}}}{{\text{e}}^{{\beta _m}t}} + {{\text{e}}^{{\beta _m}t}}\int\limits_0^t {\frac{{{\text{d}}g(\tau )}}{{{\text{d}}\tau }}{{\text{e}}^{ - {\beta _m}\tau }}{\text{d}}\tau } } \right] 。 $$ (40) （4）继续令$t \to 0$，${r_{\text{d}}} \to 0$，${r_{\text{p}}} \to 0$，且当外部荷载为瞬时施加时，式（40）可退化为Terzaghi[22]天然地基一维固结解答：
$$ U(t){\text{ = }}1 - \sum\limits_{m = 1}^\infty {\frac{2}{{{M^2}}}{{\text{e}}^{ - {M^2}{T_{\text{v}}}}}} \text{，} $$ (41) 式中，$ {T_{\text{v}}} $为土体的竖向时间因子，$ {T_{\text{v}}} = {c_{\text{v}}}t/{H^2} $，其中$ {c_{\text{v}}} $为土体的竖向固结系数，$ {c_{\text{v}}} = {k_{\text{v}}}{E_{\text{s}}}/{\gamma _{\text{w}}} $。
通过将本文解答经退化研究可得，在不同条件下本文解答可退化为已有的解析解答，这从理论的角度对本文解答的正确性进行了验证。同时，上述学者的解答可视为本文解答的特例，故本文解答具有更好的适用性。
3. 固结性状分析
本节利用本文解答对多元复合地基的固结性状进行参数敏感性分析。排水板采用市面常见的规格型，宽100 mm，厚4 mm，此排水板按照环形等效原则得其面积折减系数约为0.116。本文的对比采用径向时间因子${T_{\text{h}}} = {k_{\text{h}}}{E_{{\text{com}}}}t/(4R_{\text{n}}^2{\gamma _{\text{w}}})$为横坐标。计算参数取值见表 1。
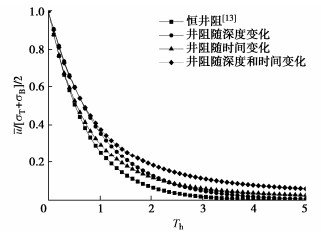
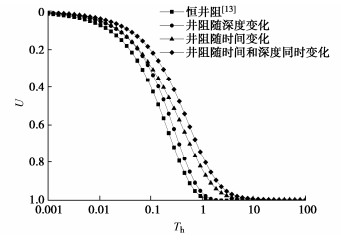
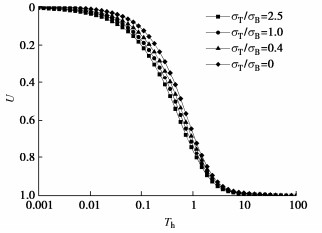
表 1 模型参数取值表Table 1. Values of model parametersH/m H/Rn rd/m rp/m rsd/rd rsp/rp ksd/kh ksp/kh kv/(10-9m·s-1) kh/kv k0/(10-5m·s-1) k0/(10-5m·s-1) Es/MPa Ep/Es Ed/Es σ0/kPa σB/kPa σT/kPa ${\theta _1}$ ${\theta _2}$ ${\theta _3}$/(10-7 1·s-1) Th 13 10 0.033 0.25 2 3 1/3 0.3 1.63 2 5.5 5.5 1.68 50 1 10 10 25 1 0.01 2.6 1 注：表中${\sigma _{\text{T}}}$和${\sigma _{\text{B}}}$分别为复合地基顶面和底面处的附加应力值。 图 3，4分别为考虑排水板不同井阻效应下复合地基的平均孔压随时间消散的曲线和固结度的对比曲线，包括卢萌盟等[13]考虑排水板为恒井阻的多元复合地基解、本文推导的考虑排水板井阻随深度变化、井阻随时间变化、以及井阻随时间和深度同时变化4种情况下的对比。由图 3，4可得，复合地基的孔压消散和地基固结最快和最慢的情况分别为考虑恒井阻和井阻随时间和深度同时变化的情况；相比于恒井阻的情况，考虑井阻随时间和深度同时变化时复合地基的孔压消散速率减慢的趋势可看作单一因素减慢趋势的叠加；考虑井阻随深度变化对复合地基孔压消散的影响随着固结的发展逐渐减弱，而考虑井阻仅随时间变化对复合地基的孔压消散影响则随着固结的发展而增大。
![]()
图 3 不同井阻效应下复合地基的平均孔压随时间消散的曲线Figure 3. Curves of average pore pressure of composite foundation dissipating with time under different well resistance effects![]()
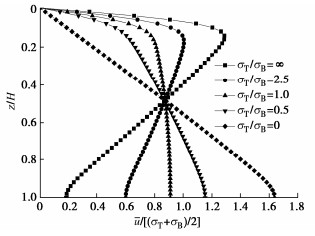
图 4 不同井阻效应下复合地基总平均固结度的对比Figure 4. Comparison of total average consolidation degrees of composite foundation under different well resistance effects图 5，6分别为不同附加应力下复合地基的平均孔压沿深度的分布曲线和对地基固结度的影响曲线图。由图 5可得，本文假设地基底面为不透水面，地基深处的孔隙水压力明显大于上部地基的水压力，表明地基深处的孔隙水压力消散要远慢于上部地基，并且在复合地基顶面的附加应力越大，地基深处的孔隙水压力消散越快。由图 6可得，在假定地基表面为透水面而底面为不透水面时，地表处的附加应力值越大地基的固结越快。
![]()
图 5 不同附加应力沿深度分布形式下复合地基的平均孔压沿深度的分布曲线Figure 5. Distribution curves of average pore pressure along depth of composite foundation with different additional stress distribution forms along depth![]()
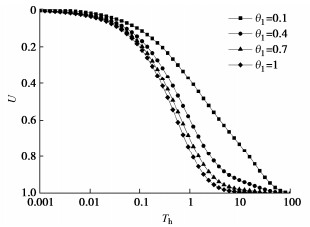
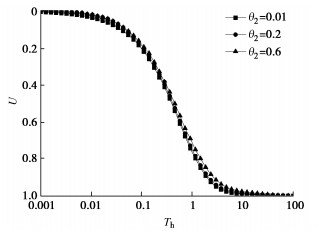
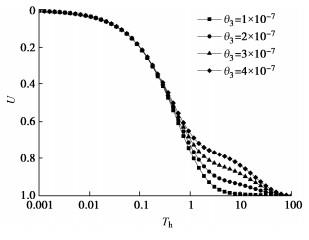
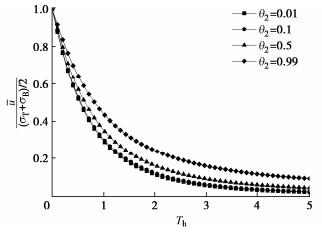
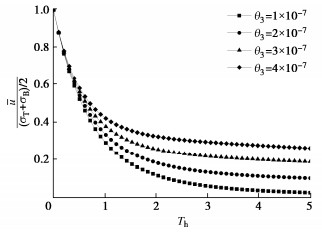
图 6 不同附加应力沿深度分布形式对复合地基总平均固结度的影响Figure 6. Influences of different additional stress distribution forms along depth on total average consolidation degree of composite foundation图 7~9分别为不同${\theta _1}$、${\theta _2}$和${\theta _3}$值对多元复合地基总平均固结度的影响曲线。由图 7~9可得，随着塑料排水板的井阻因子${\theta _1}$的增大，复合地基的固结曲线左移，表明复合地基的固结速率增大；井阻因子${\theta _2}$对复合地基固结影响甚微，随着井阻因子${\theta _2}$增大，复合地基的固结速率稍有减小；增大塑料排水板的井阻因子${\theta _3}$对于固结前期影响甚微，但对于后期固结速率影响较大，复合地基固结后期的固结速率随${\theta _3}$增大而减小，且当${\theta _3}$较大时，多元复合地基在固结后期由于径向排水明显减弱，仅通过竖向渗流继续固结，也可达到复合地基完全固结。
![]()
图 7 不同${\theta _1}$值对固结度的影响Figure 7. Influences of different values of ${\theta _1}$ on consolidation degree![]()
图 8 不同${\theta _2}$值对固结度的影响Figure 8. The effect of different ${\theta _2}$ values on the degree of consolidation![]()
图 9 不同${\theta _3}$值对固结度的影响Figure 9. Influences of different values of ${\theta _3}$on consolidation degree图 10~12分别为复合地基深度在H/2时排水板的井阻因子${\theta _1}$、${\theta _2}$和${\theta _3}$对复合地基的平均超静孔压消散的影响曲线。由图 10~12可得，随着${\theta _1}$的减小，${\theta _2}$和${\theta _3}$的增大，复合地基的平均超静孔压消散速率减慢。经对比后发现，对复合地基的平均孔压消散的影响最明显的是${\theta _3}$，其次是${\theta _1}$，然后是${\theta _2}$。
![]()
图 10 不同${\theta _1}$值对复合地基的平均孔压消散的影响Figure 10. Influences of different values of ${\theta _1}$ on dissipation of average pore pressure of composite foundation![]()
图 11 不同${\theta _2}$值对复合地基的平均孔压消散的影响Figure 11. Influences of different values of ${\theta _2}$ on dissipation of average pore pressure of composite foundation![]()
图 12 不同${\theta _3}$值对复合地基的平均孔压消散的影响Figure 12. Influences of different values of ${\theta _3}$ on dissipation of average pore pressure of composite foundation4. 工程案例分析
Zhang等[23]在临连高速的CK0+850—CK1+500段进行了塑料排水板联合粉喷桩的多元复合地基现场试验。排水板和粉喷桩按三角形布置，间距为1.8 m，长度均为10.5 m，排水板宽100 mm，厚4 mm，该复合地基${n_{\text{p}}} = 1$。试验段路堤可视为两个加载阶段，第一阶段为77 d内匀速填筑至4 m；第二阶段为4 d匀速填筑至6 m，之后保持不变。该加载过程简化为二级线性加载。试验中给出的基本参数及取值如表 2所示。
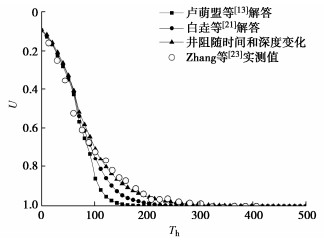
表 2 基本参数及取值Table 2. Basic parameters and valuesH/m Rn/m rd/m rp/m Asd/Ad kv/(10-9 m·s-1) kh/kv kh/ksd kd/(10-6m3·s-1) Es/MPa Ep/Es 10.5 1.039 0.033 0.25 9 1.61 2 3 35 1.25 9.4 图 13为本文考虑排水板的淤堵随时间和深度同时变化的解答、白垚等[21]考虑淤堵仅随时间变化的多元复合地基的解答、卢萌盟等[13]考虑排水板为恒井阻的多元复合地基的解答与Zhang等[23]现场实测值的对比。由图 13可得，在固结前期，固结曲线与实测值均较为吻合，但随着固结的发展，卢萌盟等[13]解答固结最快，其次是白垚等[21]的解答，最后是考虑淤堵随时间和深度同时变化的解答，且本文的工况下与现场实测值拟合最好，这是由于本文考虑了排水板的淤堵效应，因此固结后期排水速率明显减小。实际上，在试验进行到102 d，即固结度为75%左右时，在较短时间内路堤高度从4 m填筑至6 m，荷载短时间内增大，卢萌盟等[13]未考虑淤堵效应的解答相应地产生了固结加快的响应，而实测值与本文的解答则未产生明显加快的现象。产生此现象的原因为：随着固结的发展，排水板会产生土颗粒堵塞排水通道，导致排水板的井阻变大，排水功效降低，因此固结速率也不会产生加快的预期效果。
![]()
图 13 固结度的理论解和实测值的对比Figure 13. Comparison between theoretical solutions and measured values of consolidation degree5. 结论
本文推导了考虑排水板淤堵效应随时间和深度同时变化的多元组合桩复合地基的固结理论。假定排水板的渗透系数随时间呈指数型衰减且沿深度呈线性衰减，同时将排水板的涂抹效应、水泥搅拌桩的扰动效应以及土体的竖向和径向渗流考虑在内，通过推导得出多元复合地基的固结控制方程及其解答，最后对该多元复合地基的固结性状进行对比分析，得到以下4点结论。
（1）本文解答可退化到多种已有工况解答，从理论和必要性上证明了解答的合理性；另外，通过与现场试验实测数据对比，进一步验证了本文解答的有效性与精确性。
（2）相比于恒井阻的情况，考虑井阻随时间和深度同时变化时复合地基的孔压消散和固结减慢，且减慢的趋势可看作单一影响因素减慢趋势的叠加；考虑井阻随深度分布变化对复合地基的孔压消散和固结的影响随着固结的发展逐渐减弱，而考虑井阻仅随时间变化对复合地基的孔压消散和固结的影响则随着固结过程而增大。
（3）多元复合地基深处的孔压要明显大于上部地基的孔压，即地基深处的孔压消散较慢；地表处的附加应力越大，复合地基的固结速率越大，地基深处的孔压消散越快。
（4）当${\theta _1}$减小或${\theta _2}$增大时，多元复合地基的平均孔压消散速率和固结速率均减小；${\theta _3}$的增大对多元复合地基的平均孔隙水压力消散速率和后期固结速率的减小有显著影响；当${\theta _3}$较大时，由于径向固结减弱，固结后期地基仅靠竖向渗流达到完全固结。
-
![]()
图 3 不同井阻效应下复合地基的平均孔压随时间消散的曲线
Figure 3. Curves of average pore pressure of composite foundation dissipating with time under different well resistance effects
![]()
图 4 不同井阻效应下复合地基总平均固结度的对比
Figure 4. Comparison of total average consolidation degrees of composite foundation under different well resistance effects
![]()
图 5 不同附加应力沿深度分布形式下复合地基的平均孔压沿深度的分布曲线
Figure 5. Distribution curves of average pore pressure along depth of composite foundation with different additional stress distribution forms along depth
![]()
图 6 不同附加应力沿深度分布形式对复合地基总平均固结度的影响
Figure 6. Influences of different additional stress distribution forms along depth on total average consolidation degree of composite foundation
![]()
图 7 不同θ1值对固结度的影响
Figure 7. Influences of different values of θ1 on consolidation degree
![]()
图 8 不同θ2值对固结度的影响
Figure 8. The effect of different θ2 values on the degree of consolidation
![]()
图 9 不同θ3值对固结度的影响
Figure 9. Influences of different values of θ3on consolidation degree
![]()
图 10 不同θ1值对复合地基的平均孔压消散的影响
Figure 10. Influences of different values of θ1 on dissipation of average pore pressure of composite foundation
![]()
图 11 不同θ2值对复合地基的平均孔压消散的影响
Figure 11. Influences of different values of θ2 on dissipation of average pore pressure of composite foundation
![]()
图 12 不同θ3值对复合地基的平均孔压消散的影响
Figure 12. Influences of different values of θ3 on dissipation of average pore pressure of composite foundation
![]()
图 13 固结度的理论解和实测值的对比
Figure 13. Comparison between theoretical solutions and measured values of consolidation degree
表 1 模型参数取值表
Table 1 Values of model parameters
H/m H/Rn rd/m rp/m rsd/rd rsp/rp ksd/kh ksp/kh kv/(10-9m·s-1) kh/kv k0/(10-5m·s-1) k0/(10-5m·s-1) Es/MPa Ep/Es Ed/Es σ0/kPa σB/kPa σT/kPa θ1 θ2 θ3/(10-7 1·s-1) Th 13 10 0.033 0.25 2 3 1/3 0.3 1.63 2 5.5 5.5 1.68 50 1 10 10 25 1 0.01 2.6 1 注：表中σT和σB分别为复合地基顶面和底面处的附加应力值。 
下载: 导出CSV
表 2 基本参数及取值
Table 2 Basic parameters and values
H/m Rn/m rd/m rp/m Asd/Ad kv/(10-9 m·s-1) kh/kv kh/ksd kd/(10-6m3·s-1) Es/MPa Ep/Es 10.5 1.039 0.033 0.25 9 1.61 2 3 35 1.25 9.4
下载: 导出CSV
-
[1] 郑俊杰, 区剑华, 吴世明, 等. 多元复合地基的理论与实践[J]. 岩土工程学报, 2002, 24(2): 208-212. doi: 10.3321/j.issn:1000-4548.2002.02.018 ZHENG Junjie, OU Jianhua, WU Shiming, et al. Theory and practice of multi-element composite ground[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 208-212. (in Chinese) doi: 10.3321/j.issn:1000-4548.2002.02.018
[2] 郑刚, 龚晓南, 谢永利, 等. 地基处理技术发展综述[J]. 土木工程学报, 2012, 45(2): 127-146. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201202020.htm ZHENG Gang, GONG Xiaonan, XIE Yongli, et al. State-of-the-art techniques for ground improvement in China[J]. China Civil Engineering Journal, 2012, 45(2): 127-146. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201202020.htm
[3] 龚晓南. 复合地基理论及工程应用[M]. 3版. 北京: 中国建筑工业出版社, 2018: 430-431. GONG Xiaonan. Composite Foundation Theory and Engineering Application[M]. 3rd ed. Beijing: China Architecture & Building Press, 2018: 430-431. (in Chinese)
[4] ZHANG D, LIU S, HONG Z, et al. Consolidation calculating method of soft ground improved by DJM-PVD combined method[C]//GeoShanghai International Conference 2006. June 6-8, 2006, Shanghai, China. Reston, VA, USA: American Society of Civil Engineers, 2006: 29-36.
[5] 章定文, 刘松玉. 路堤荷载下DJM-PVD复合地基固结特性数值分析[J]. 东南大学学报(自然科学版), 2008, 38(5): 828-833. doi: 10.3321/j.issn:1001-0505.2008.05.017 ZHANG Dingwen, LIU Songyu. Numerical analysis for performance of ground improved by DJM-PVD combined method[J]. Journal of Southeast University (Natural Science Edition), 2008, 38(5): 828-833. (in Chinese) doi: 10.3321/j.issn:1001-0505.2008.05.017
[6] 陈蕾, 刘松玉, 洪振舜. 排水粉喷桩复合地基固结计算方法的探讨[J]. 岩土工程学报, 2007, 29(2): 198-203. http://www.cgejournal.com/cn/article/id/12304 CHEN Lei, LIU Songyu, HONG Zhenshun. Study of consolidation calculation of soft ground improved by dry jet mixing combined with vertical drain method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(2): 198-203. (in Chinese) http://www.cgejournal.com/cn/article/id/12304
[7] 刘吉福. 路堤下等应变复合地基的固结分析[J]. 岩石力学与工程学报, 2009, 28(增刊1): 3042-3050. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2009S1069.htm LIU Jifu. Analysis of consolidation of equal-strain composite ground under embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 3042-3050. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2009S1069.htm
[8] YE G B, ZHANG Z, XING H F, et al. Consolidation of a composite foundation with soil–cement columns and prefabricated vertical drains[J]. Bulletin of Engineering Geology and the Environment, 2012, 71(1): 87-98. doi: 10.1007/s10064-011-0354-y
[9] 叶观宝, 张振, 邢皓枫, 等. 组合型复合地基固结分析[J]. 岩土工程学报, 2011, 33(1): 45-49. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202107014.htm YE Guanbao, ZHANG Zhen, XING Haofeng, et al. Consolidation of combined composite foundation[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 45-49. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202107014.htm
[10] ZHANG Z, XING H, YE G. Consolidation analysis of soft soil improved with short deep mixed columns and long prefabricated vertical drains (PVDs)[J]. Geosynthetics International, 2015, 22(5): 366-379. doi: 10.1680/jgein.15.00018
[11] 杨涛, 李超. 刚性基础下组合渗流碎石桩–不排水桩复合地基固结分析[J]. 岩石力学与工程学报, 2018, 37(11): 2631-2640. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201811022.htm YANG Tao, LI Chao. Consolidation analysis of stone column-impervious pile composite ground underneath rigid foundation considering radial and vertical flows within stone columns[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(11): 2631-2640. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201811022.htm
[12] LU M M, JING H W, ZHOU Y, et al. General analytical model for consolidation of stone column–reinforced ground and combined composite ground[J]. International Journal of Geomechanics, 2017, 17(6): 04016131. doi: 10.1061/(ASCE)GM.1943-5622.0000836
[13] 卢萌盟, 白垚, 李红军, 等. 多元组合桩复合地基固结解析模型与解答[J]. 岩石力学与工程学报, 2021, 40(增刊2): 3301-3312. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2021S2030.htm LU Mengmeng, BAI Yao, LI Hongjun, et al. Analytical models and solutions for consolidation of composite foundation with multiple types of reinforcements[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(S2): 3301-3312. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2021S2030.htm
[14] DENG Y B, XIE K H, LU M M, et al. Consolidation by prefabricated vertical drains considering the time dependent well resistance[J]. Geotextiles and Geomembranes, 2013, 36: 20-26.
[15] DENG Y B, XIE K H, LU M M. Consolidation by vertical drains when the discharge capacity varies with depth and time[J]. Computers and Geotechnics, 2013, 48: 1-8.
[16] 郭霄, 谢康和, 吕文晓, 等. 井阻随深度和时间变化的竖井地基固结解析解[J]. 岩土工程学报, 2015, 37(6): 996-1001. doi: 10.11779/CJGE201506004 GUO Xiao, XIE Kanghe, LÜ Wenxiao, et al. Analytical solutions for consolidation by vertical drains with variation of well resistance with depth and time[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(6): 996-1001. (in Chinese) doi: 10.11779/CJGE201506004
[17] 江文豪, 詹良通, 杨策, 等. 考虑井阻随时间变化及径-竖向渗流下砂井地基固结的解析解及其分析[J]. 工程力学, 2021, 38(6): 218-226, 256. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202106020.htm JIANG Wenhao, ZHAN Liangtong, YANG Ce, et al. Analytical solution and analysis for consolidation of sand-drained ground considering the time-dependent well resistance and radial-vertical flow[J]. Engineering Mechanics, 2021, 38(6): 218-226, 256. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX202106020.htm
[18] 卢萌盟, 张强, 靖洪文, 等. 基于环形等效的排水板地基固结[J]. 岩石力学与工程学报, 2018, 37(2): 513-520. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201802023.htm LU Mengmeng, ZHANG Qiang, JING Hongwen, et al. Consolidation of band-shaped drain based on equivalent annular drain[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(2): 513-520. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201802023.htm
[19] 谢康和, 曾国熙. 等应变条件下的砂井地基固结解析理论[J]. 岩土工程学报, 1989, 11(2): 3-17. http://www.cgejournal.com/cn/article/id/9256 XIE Kanghe, ZENG Guoxi. Consolidation theories for drain wells under equal strain condition[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(2): 3-17. (in Chinese) http://www.cgejournal.com/cn/article/id/9256
[20] LU M M, JING H W, ZHOU A N, et al. Analytical models for consolidation of combined composite ground improved by impervious columns and vertical drains[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42(6): 871-888.
[21] 白垚, 卢萌盟, 杨康, 等. 考虑变井阻的多元复合地基固结理论研究[J/OL]. 工程力学. doi: 10.6052/j.issn.1000-4750.2022.05.0439. BAI Yao, LU Mengmeng, YANG Kang, et al. Study on the consolidation behaviors of multi-reinforcement composite foundation considering time-dependent well resistance[J/OL]. Engineering Mechanics. doi: 10.6052/j.issn.1000-4750.2022.05.0439.(inChinese).
[22] TERZAGHE K. Theoretical Soil Mechanics[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 1943.
[23] ZHANG D W, LIU S Y, HAN W J, et al. A combined dry jet mixing-prefabricated vertical drain method for soft ground improvement: a case study[J]. Marine Georesources & Geotechnology, 2013, 31(4): 332-347.
-
期刊类型引用(3)
1. 蔡袁强，叶晓倩，史吏. 考虑泊松效应的流泥轴对称真空过滤理论. 岩土工程学报. 2025(02): 243-254 . 
本站查看
2. 裘友强，张留俊，刘洋，刘军勇，尹利华. “双碳”背景下公路软土地基处理技术研究进展. 水利水电技术(中英文). 2025(01): 113-131 . 百度学术
3. 许宝龙，卢萌盟. 考虑淤堵效应的多元排水体复合地基固结解析解. 岩石力学与工程学报. 2025(04): 1053-1064 . 百度学术
其他类型引用(3)
-
其他相关附件
-
本文英文pdf
点击下载(781KB) -
PDF格式
03-202308-G22-0590一文审稿意见与作者答复 点击下载(513KB)
-
计量
- 文章访问数: 814
- HTML全文浏览量: 48
- PDF下载量: 144
- 被引次数: 6
