Application and analysis of horizontal permeable reaction barrier in risk mitigation of VOC vapor in contaminated sites
-
摘要: 水平渗透性反应屏障（HPRB）是一种针对包气带中挥发性有机化合物（VOC）蒸气的被动修复技术，具有运行无耗能的优点，能够作为大范围VOC污染场地长效风险管控措施。本文提出了VOC蒸气在含HPRB的层状土中迁移的一维瞬态半解析模型，采用Laplace变换得到Laplace域下的通解后，采用Talbot数值方法实现Laplace逆变换得到时间域下的VOC蒸气迁移的半解析解。解析模型计算结果和数值模型的结果吻合良好。算例结果表明，HPRB更适用于原位土体扩散系数较低的污染场地；HPRB埋深过大不利于VOC蒸气的去除；增加HPRB厚度能有效去除场地中的VOC蒸气；污染源质量浓度衰减系数增加会降低场地中VOC蒸气峰值质量浓度，不考虑污染源质量浓度衰减会导致HPRB的设计过于保守。最后提出了HPRB埋深和厚度的设计思路。Abstract: The horizontal permeable reaction barrier (HPRB) is a passive remediation technology for the volatile organic compound (VOC) vapor in the vadose zone. It has the advantage of consuming less energy during the operation. And it can be used as a long-term risk control measure for the large-scale VOC contaminated sites. A transient analytical model is proposed in this study to simulate the VOC vapor migration in the layered soil containing a layer of the HPRB. The Laplace transformation is adopted to derive the general solution in the Laplace domain, and then the Laplace inversion of the numerical Talbot method is adopted to derive the semi-analytical solution of the VOC vapor migration. It is found that the HPRB is more suitable for the contaminated sites with low effective diffusivity soil. The large depth of the HPRB is not conducive to the removal of the VOC vapor. The increase of thickness of the HPRB enhances the removal of the VOC vapor. The increase of the source concentration decay rate can reduce the peak value of the VOC concentration in the contaminated sites. The neglect of the source decay can lead to the excessively conservative design of the HPRB. Finally, the design procedure of the depth and thickness of the HPRB is proposed.
-
0. 引言
地下储罐泄露、污水管线泄露以及工厂旧址土壤残余污染等因素都会导致场地中的土壤和地下水受到挥发性有机化合物（VOC）污染[1]。由于VOC污染物易挥发的特性，VOC蒸气会从受VOC污染的地下水或者土壤中挥发出，并在土壤中发生迁移。土壤中VOC蒸气迁移出地表或者入侵污染场地周边的建筑都会威胁污染场地周边人群的生命健康。因此亟需开展土壤中VOC蒸气迁移以及处理方法的研究。对于有机污染场地，目前常用的有机污染土原位修复技术包括气相抽提技术、原位热处理技术、原位化学氧化技术和微生物修复技术等[2-3]。其中气相抽提技术是最常用的原位修复技术之一，能够有效降低污染土壤中的VOC蒸气质量浓度。但气相抽提技术运行周期较长，且抽提出的VOC蒸气仍需要进行后处理降低毒性，一定程度上增加了工程成本[4]。近年来，Mahmoodlu等[5]提出了采用水平渗透性反应屏障（HPRB）来限制包气带中VOC蒸气的迁移，利用VOC蒸气与HPRB中的修复药剂发生的化学反应将VOC蒸气转化为无害产物，减小土壤中VOC蒸气迁移造成的危害。HPRB技术对土壤中VOC蒸气的去除效率高，运行期间能源消耗少，是一种比气相抽提技术更经济的污染场地长效管控措施。
为了研究HPRB对VOC蒸气的去除效果，已有学者展开了相关的试验研究[4-7]。Mahmoodlu等[4]通过开展室内试验发现高锰酸钾固体颗粒能够将VOC蒸气氧化成低毒性的产物，且VOC蒸气的氧化反应满足线性氧化动力学模型。随后，Mahmoodlu等[5-6]通过将高锰酸钾固体颗粒和砂土颗粒混合制成HPRB，开展室内土柱试验研究HPRB饱和度、厚度与深度等多种因素对VOC蒸气去除效率的影响。除了采用高锰酸钾固体氧化VOC蒸气以外，Zingaretti等[7]提出采用零价铁固体颗粒作为HPRB中的反应材料，并开展室内试验研究了零价铁固体对三氯乙烯（TCE）蒸气的去除效果。上述试验研究皆表明HPRB能够有效去除VOC蒸气，能够避免VOC蒸气从污染场地逸出造成危害。
目前针对VOC蒸气在含HPRB土层中迁移反应的解析模型研究较少。Verginelli等[8]建立了VOC蒸气在HPRB中迁移的一维瞬态解析模型，该模型包含非饱和原位土体以及HPRB两层土。其计算结果表明采用HPRB去除土壤中的VOC蒸气的成本明显低于气相抽提技术；但是，该解析模型在求解VOC蒸气于原位土体中迁移时采用了半无限域解答，与有限厚度的原位土体相矛盾，且无法考虑成层土体。土层的成层特性在自然界中普遍存在，且对VOC蒸气在土层中的迁移有显著影响。对于VOC蒸气在层状土中迁移的解析模型也并不少见[9-12]。其中，Xie等[12]提出了VOC蒸气在填埋场四层复合封顶系统中扩散-降解的解析解，其中考虑了VOC蒸气在土工膜表面的分配系数以及在其它土层中的降解。但是不同于Xie等[12]考虑的填埋场复合封顶系统的4层结构，含HPRB的污染场地中不含有土工膜，而且自然界中的土层数可能多于四层。因此，有必要在前人模型研究基础上提出VOC蒸气在含HPRB的层状土中迁移的瞬态解析模型。
本文考虑了VOC蒸气在含HPRB的污染场地中的扩散、吸附以及氧化反应，提出了层状土污染场地下VOC蒸气一维迁移瞬态解析模型，并进行验证。随后分析了场地中土层参数、HPRB厚度和埋深、污染源深度和质量浓度衰减系数等因素对VOC蒸气迁移与反应的影响。最后，提出了VOC污染场地中HPRB的设计思路，为实际工程提供参考。
1. 污染物蒸气迁移反应模型的建立与验证
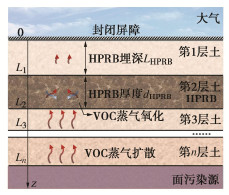
针对VOC污染场地中挥发出的VOC蒸气，提出采用HPRB对VOC蒸气进行氧化处理，减小VOC蒸气逸出危害。VOC蒸气在含HPRB的成层土中的迁移概念模型如图 1所示。HPRB层由砂土和反应药剂（如高锰酸钾）混合制成[5-6]；上部土层为回填土，回填土的上方设置有封闭屏障阻止通过HPRB的VOC蒸气逸出；下部土层为原位土体，其中原位土体可能为层状土。VOC蒸气在回填土和原位土体中发生扩散和吸附，在HPRB中除了扩散和吸附外，还会溶解在HPRB中的孔隙水中与被同样溶解在孔隙水中的高锰酸钾氧化而发生化学反应[5]。针对VOC蒸气在含HPRB的成层土中迁移反应过程，提出了相应的VOC蒸气一维迁移瞬态解析模型。
![]()
图 1 VOC蒸气在含HPRB土层中迁移概念模型图Figure 1. Schematic graph of migration of VOC vapor in layered soil containing HPRB1.1 基本假定
计算模型的假定如下：①污染源为空间范围足够大的面污染源，污染物源质量浓度空间分布均匀，因此本模型可以简化为一维模型；②各土层为均质土层，土层参数不随深度发生变化；③HPRB中高锰酸钾固体的含量充足，HPRB中的氧化剂质量浓度等于其溶解；④VOC蒸气迁移过程中，土壤温度、pH值以及含水率等保持恒定；⑤VOC蒸气在土层中迁移形式以扩散为主，不考虑VOC蒸气的对流。
1.2 控制方程与边界条件
第i层土中VOC蒸气一维运移的控制方程如下：
$$ {R_i}\frac{{\partial {c_i}(z, t)}}{{\partial t}} = {D_i}\frac{{{\partial ^2}{c_i}(z, t)}}{{\partial {z^2}}} - \frac{{{\varphi _{{\text{w}}, i}}{{k''}_i}{c_{{\text{ox}}i}}}}{{{H_{\text{m}}}}}{c_i}(z, t) \text{，} $$ (1) 其中，
$$ {k''_i} = \left[ {H(z - {L_{{\text{HPRB}}}}) - H(z - {L_{{\text{HPRB}}}} - {d_{{\text{HPRB}}}})} \right]{k_{{\text{HPRB}}}} 。 $$ (2) 式中：ci为VOC蒸气质量浓度；Ri为阻滞因子；Di为VOC蒸气在土层中的有效扩散系数；φw, i为土层含水孔隙率；Hm为VOC蒸气的无量纲亨利常数；coxi为HPRB层中氧化剂质量浓度；$ {k''_i} $为土层中的二阶化学反应速率，在回填土和原位土体中，$ {k''_i} $为0，在HPRB层中，$ {k''_i} $等于VOC蒸气的二阶反应速率（kHPRB）；dHPRB和LHPRB分别为HPRB层的厚度与埋深。单位阶跃函数H(x)可定义为
$$ H(x)=\left\{\begin{array}{ll} 1 & (x>0) \\ 0 & (x \leqslant 0) \end{array} 。\right.$$ (3) VOC蒸气在土层中的有效扩散系数采用Millington-Quirk公式计算[13]：
$$ {D_i} = {D_{\text{a}}}\varphi _{{\text{a}}, i}^{10/3}/\varphi _{{\text{t, i}}}^2 + {D_{\text{w}}}\varphi _{{\text{w}}, i}^{10/3}/({H_{\text{m}}}\varphi _{{\text{t, }}i}^2) 。 $$ (4) 式中：φt, i为土层总孔隙率；φa, i为土层含气孔隙率；Da和Dw分别为VOC蒸气在大气和水中的扩散系数。
土层对VOC蒸气的阻滞因子可以通过下式计算得到：
$$ {R_i} = \varphi _{{\text{a}}, i}^{} + \varphi _{{\text{w}}, i}^{}/{H_{\text{m}}} + {K_{{\text{oc}}}}{f_{{\text{oc}}, i}}{\rho _{{\text{b}}, i}}/{H_{\text{m}}} 。 $$ (5) 式中：Koc为有机碳对VOC的吸附系数；foc, i为土层中有机碳的质量分数；ρb, i为土层的密度。
现有试验研究表明，HPRB中的含水率、pH值以及药剂颗粒的比表面积都会影响VOC蒸气的去除效率。HRPB中含水率提高能够有效提高VOC蒸气的去除效率[6]。强酸性或者强碱性的反应条件会减小药剂与VOC蒸气的反应速率[5-6]。药剂颗粒的比表面积增加能够提高VOC蒸气的去除效率，其影响主要体现在VOC蒸气二阶反应速率的提高[7]。由式（1）可见本文建立的模型能够考虑HPRB含水率以及VOC蒸气二阶反应速率对VOC蒸气去除效率的影响。
由于在地表采用了封闭屏障阻碍穿过HPRB的VOC蒸气逸出，模型的上边界满足第二类边界条件：
$$ \frac{{\partial {c_1}(0, t)}}{{\partial z}} = 0 。 $$ (6) 本模型的下边界为质量浓度均匀分布的面污染源，污染源处的VOC蒸气质量浓度满足第一类边界条件：
$$ {c_n}(L, t) = {H_{\text{m}}}{c_{{\text{gw}}}}{{\text{e}}^{ - {k_{{\text{gw}}}}t}} 。 $$ (7) 式中：cgw为地下水中VOC初始质量浓度；kgw为污染源质量浓度的衰减系数，当kgw=0的时候，污染源为恒定质量浓度源。
模型的初始条件为
$$ {c_i}(z, 0) = 0 。 $$ (8) 各土层间的界面需要满足质量浓度与通量连续条件，其表达式可写为
$$ \left.\begin{array}{l} c_{i-1}\left(L_{i-1}, t\right)=c_i\left(L_{i-1}, t\right), \\ D_{i-1} \frac{\partial c_{i-1}\left(L_{i-1}, t\right)}{\partial z}=D_i \frac{\partial c_i\left(L_{i-1}, t\right)}{\partial z} 。 \end{array}\right\}$$ (9) 1.3 模型求解
采用Laplace变换将时域下的控制方程（式1）转换为如下Laplace域下的控制方程：
$$ {D_i}\frac{{{{\text{d}}^2}{{\bar c}_i}(z, s)}}{{{\text{d}}{z^2}}} - \left( {\frac{{{\varphi _{{\text{w}}, i}}{{k''}_i}{c_{{\text{ox}}i}}}}{{{H_{\text{m}}}}} + s{R_i}} \right){\bar c_i}(z, s) = 0 。 $$ (10) 该模型在Laplace域下的边界条件可以写为
$$ \left.\begin{array}{l} \frac{\mathrm{d} \bar{c}_1(0, s)}{\mathrm{d} z}=0, \\ \bar{c}_n(L, s)=H_{\mathrm{m}} c_{\mathrm{gw}} /\left(s+k_{\mathrm{gw}}\right) 。 \end{array}\right\}$$ (11) Laplace域下各土层间的连续条件可写为
$$ \left.\begin{array}{l} \bar{c}_i\left(L_{i-1}, s\right)=\bar{c}_{i-1}\left(L_{i-1}, s\right), \\ D_i \frac{\mathrm{d} \bar{c}_i\left(L_{i-1}, s\right)}{\mathrm{d} z}=D_{i-1} \frac{\mathrm{d} \bar{c}_{i-1}\left(L_{i-1}, s\right)}{\mathrm{d} z} 。 \end{array}\right\}$$ (12) 可以解得控制方程式（10）的通解为
$$ {\bar c_i}(z, s) = {A_i}{{\text{e}}^{{P_i}z}} + {B_i}{{\text{e}}^{ - {P_i}z}} \text{，} $$ (13) $$ {P_i} = \sqrt {{{\left( {{\varphi _{{\text{w}}, i}}{{k''}_i}{c_{{\text{ox}}i}} + s{H_{\text{m}}}{R_i}} \right)} \mathord{\left/ {\vphantom {{\left( {{\varphi _{{\text{w}}, i}}{{k''}_i}{c_{{\text{ox}}i}} + s{H_{\text{m}}}{R_i}} \right)} {\left( {{H_{\text{m}}}{D_i}} \right)}}} \right. } {\left( {{H_{\text{m}}}{D_i}} \right)}}} 。 $$ (14) 将式（13）代入层间连续条件式（12）后可得
$$ \left.\begin{array}{l} A_i \mathrm{e}_i^{P_i L_{i-1}}+B_i \mathrm{e}^{-P_i L_{i-1}}=A_{i-1} \mathrm{e}^{P_{i-1} L_{i-1}}+B_{i-1} \mathrm{e}^{-P_{i-1} L_{i-1}}, \\ \frac{D_i P_i}{D_{i-1} P_{i-1}}\left(A_i \mathrm{e}^{P_i L_{i-1}}-B_i \mathrm{e}^{-P_i L_{i-1}}\right)=A_{i-1} \mathrm{e}^{P_{i-1} L_{i-1}}-B_{i-1} \mathrm{e}^{-P_{i-1} L_{i-1}}。 \end{array}\right\} $$ (15) 基于式（15）可建立如下传递矩阵确定各层通解中待定系数Ai和Bi的相对关系：
$$ \left[ {\begin{array}{*{20}{c}} {{A_i}} \\ {{B_i}} \end{array}} \right] = {{\boldsymbol{F}}_{i - 1}}\left[ {\begin{array}{*{20}{c}} {{A_{i - 1}}} \\ {{B_{i - 1}}} \end{array}} \right] \text{，} $$ (16) 其中，
$$ {{\boldsymbol{F}}_{i - 1}} = \frac{1}{{ - 2{D_i}{P_i}}}\left[ {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}} \\ {{T_{21}}}&{{T_{22}}} \end{array}} \right] \text{，} $$ (17) $$ {T_{11}} = ( - {D_{i - 1}}{P_{i - 1}} - {D_i}{P_i}){{\text{e}}^{\left( {{P_{i - 1}} - {P_i}} \right){L_{i - 1}}}} \text{，} $$ (18) $$ {T_{12}} = ({D_{i - 1}}{P_{i - 1}} - {D_i}{P_i}){{\text{e}}^{ - \left( {{P_{i - 1}} + {P_i}} \right){L_{i - 1}}}} \text{，} $$ (19) $$ {T_{21}} = ({D_{i - 1}}{P_{i - 1}} - {D_i}{P_i}){{\text{e}}^{\left( {{P_{i - 1}} + {P_i}} \right){L_{i - 1}}}} \text{，} $$ (20) $$ {T_{22}} = ( - {D_{i - 1}}{P_{i - 1}} - {D_i}{P_i}){{\text{e}}^{\left( {{P_i} - {P_{i - 1}}} \right){L_{i - 1}}}} 。 $$ (21) 将通解式（13）以及传递矩阵式（16）代入边界条件式（11）后，可建立如下方程：
$$ \frac{{{H_{\text{m}}}{c_{{\text{gw}}}}}}{{s + {k_{{\text{gw}}}}}} = \left[ {\begin{array}{*{20}{c}} {{{\text{e}}^{{P_n}L}}}&{{{\text{e}}^{ - {P_n}L}}} \end{array}} \right]{\boldsymbol{E}}\left[ {\begin{array}{*{20}{c}} {{A_1}} \\ {{A_1}} \end{array}} \right] \text{，} $$ (22) $$ {\boldsymbol{E}} = {{\boldsymbol{F}}_{n - 1}}{{\boldsymbol{F}}_{n - 2}} \cdots {{\boldsymbol{F}}_1} = \left[ {\begin{array}{*{20}{c}} {{\gamma _{11}}}&{{\gamma _{12}}} \\ {{\gamma _{21}}}&{{\gamma _{22}}} \end{array}} \right] 。 $$ (23) 第一层土通解中的待定系数A1和B1可以通过求解方程（22）得到
$$ {A_1} = \frac{{{H_{\text{m}}}{c_{{\text{gw}}}}}}{{(s + {k_{{\text{gw}}}})\left[ {({\gamma _{11}} + {\gamma _{12}}){{\text{e}}^{{P_n}L}} + ({\gamma _{21}} + {\gamma _{22}}){{\text{e}}^{ - {P_n}L}}} \right]}} \text{，} $$ (24) $$ {B_1} = {A_1} 。 $$ (25) 将待定系数A1和B1代入传递矩阵式（16）进行迭代计算即可求得各个土层通解中的待定系数。
VOC蒸气质量浓度在时域下的解答可以采用Talbot方法[14]对式（13）进行Laplace逆变换得到。如此通过Laplace变换在Laplace域下求得通解后采用数值方法对通解进行Laplace逆变换获得时间域下的半解析解的方法在污染物瞬态迁移的模型研究中也有较广泛的应用[15-16]。
在时域下，HPRB中氧化药剂的消耗总量可写为
$$ {M_{{\text{oxi}}}} = {A_{{\text{HPRB}}}}\gamma \int_0^T {\int_{{L_{{\text{HPRB}}}}}^{{L_{{\text{HPRB}}}} + {d_{{\text{HPRB}}}}} {{\varphi _{{\text{w}}, i}}{{k''}_i}{c_{{\text{oxi}}}}c(x, t)/{H_{\text{m}}}} } {\text{d}}x{\text{d}}t 。 $$ (26) 式中：AHPRB为HPRB层的覆盖面积；$ \gamma $为氧化药剂和VOC蒸气反应的化学计量比；T为HPRB的服役时间。式（26）在Laplace域下的表达式可以写为
$$ {\overline M _{{\text{oxi}}}} = \frac{{{A_{{\text{HPRB}}}}\gamma {\varphi _{{\text{w}}, i}}{{k''}_i}{c_{{\text{oxi}}}}}}{{s{H_{\text{m}}}}}\mathcal{L}\int_{{L_{{\text{HPRB}}}}}^{{L_{{\text{HPRB}}}} + {d_{{\text{HPRB}}}}} {c(x, T){\text{d}}x} 。 $$ (27) 1.4 模型验证
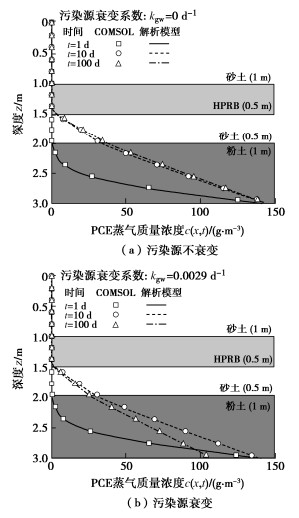
采用大型多物理场仿真有限元软件COMSOL Multiphysics建立数值模型和本文提出的解析模型计算结果进行对比验证。验证算例中的污染源深度L为3 m。污染源上方的土层自上而下依次为1 m砂土、0.5 m HPRB层、0.5 m砂土和1 m粉土，土层特征参数见表 1。
表 1 土层特征参数Table 1. Characteristic parameters of soil for simulations本文中VOC污染物类型为四氯乙烯（PCE），HPRB中的氧化剂选用高锰酸钾，模型的其他输入参数如表 2所示。高锰酸钾和PCE的化学反应方程式如下[8]：
$$ \begin{aligned} & 4 \mathrm{KMnO}_4+3 \mathrm{C}_2 \mathrm{Cl}_4+4 \mathrm{H}_2 \mathrm{O} \\ &\quad\quad\quad\quad\quad\quad \rightarrow 4 \mathrm{MnO}_2+6 \mathrm{CO}_2+4 \mathrm{~K}^{+}+8 \mathrm{H}^{+}+12 \mathrm{Cl}^{-} 。 \end{aligned} $$ (28) 表 2 模型输入参数Table 2. Input parameters used in simulation土层有机碳含量foc[21]/(kg oc/kg soil) PCE分子量/(g·mol-1) Da[18]/(m2·s-1) Dw[18]/(m2·s-1) Hm[18] Koc[18]/(L·kg-1) 地下水VOC质量浓度cgw/(mg·L-1) 污染源衰变系数kgw[20]/d-1 二阶反应速率k”[19]/(M-1·s-1) coxi/(g·L-1) KMnO4分子量/(g·mol-1) 反应的化学计量比γ[8]/(kg KMnO4/kg PCE) 0.001 165.8 5.05×10-6 9.46×10-10 0.724 94.94 200 0~0.0029 0.0084 64 L 158 4/3 本文解析模型和数值模型的计算结果的对比如图 2所示。通过对比不考虑污染源衰变（图 2（a））和考虑污染源衰变（图 2（b））两种工况不同时刻的PCE蒸气质量浓度分布，可以发现两者结果吻合良好，解析模型的正确性得以验证。
![]()
图 2 本文模型计算结果与数值解对比Figure 2. Comparison of results by proposed analytical model and numerical model2. 土层参数的影响
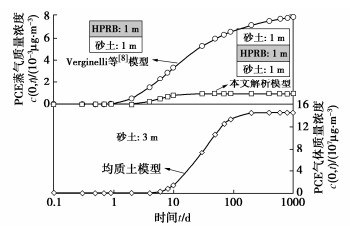
图 3对比了本文提出的解析模型、Verginelli等[8]建立的HPRB解析模型以及均质土模型的计算结果。均质土模型的计算结果代表该砂土场地不采用HPRB管控的原始工况，土层特征参数与输入参数见表 1，2。在本节的算例中污染源质量浓度保持恒定。在200 d左右封闭屏障下方的PCE蒸气质量浓度已经接近污染源处的蒸气质量浓度，土层中充满PCE蒸气，若封闭屏障存在缺陷则PCE蒸气有较大逸出风险。对于采用HPRB管控的工况，在该砂土场地中距离污染源1 m处铺设一层1 m厚的HPRB，HPRB上方回填1 m厚的回填土。基于本文提出的解析模型计算结果可以发现采用HPRB管控能够降低封闭屏障下方的PCE蒸气质量浓度超10个数量级，极大降低PCE蒸气逸出风险。对于相同HPRB管控工况，Verginelli等[8]建立的模型只能考虑1 m厚的HPRB覆盖于1 m厚的原位土上的简化工况，高估了封闭屏障下方的PCE蒸气质量浓度，其结果可能会导致HPRB的保守设计，增加管控成本。
![]()
图 3 与均质土模型和现有HPRB模型计算结果对比Figure 3. Comparison of results by proposed analytical model, homogeneous soil model and existing HPRB model2.1 HPRB层饱和度和反应速率的影响
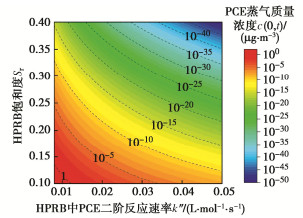
图 4中分析了HPRB饱和度和PCE蒸气二阶反应速率对封闭屏障下方PCE蒸气峰值质量浓度的影响。HPRB饱和度增加和蒸气二阶反应速率提高都会导致封闭屏障下方的PCE蒸气峰值质量浓度降低。当HPRB中PCE的反应速率为0.01 L/(mol·s)时，HPRB的饱和度从0.1提升至0.2能够降低封闭屏障下方的PCE蒸气峰值质量浓度4个数量级；而当HPRB中PCE的反应速率为0.05 L/(mol·s)时，同样将HPRB饱和度自0.1提升至0.2能够降低PCE蒸气峰值质量浓度超过10个数量级。因此，在高反应速率的条件下提升HPRB饱和度对土壤中PCE蒸气管控效果更明显。在HPRB设计中可以通过提升HPRB饱和度和调整更优的反应环境来提升HPRB对场地中污染物蒸气的管控效果。
![]()
图 4 HPRB饱和度和反应速率对PCE蒸气质量浓度的影响Figure 4. Influences of water saturation and reaction rate of HPRB on PCE vapor concentration2.2 回填土的影响
图 5为采用不同类型的土壤作为回填土的工况中封闭屏障下方PCE蒸气质量浓度随时间的变化规律。其中，原位土体为均质砂土。不同类型的回填土的土层特征参数见表 1，PCE蒸气在不同土壤中的扩散系数和阻滞因子不同。由图 5可看出，回填土有效扩散系数降低和阻滞因子提高都会减缓PCE蒸气在土层中的迁移，对于高阻滞性和低扩散性的回填土，土层中蒸气运移达到稳态所需的时间更长。在污染源不发生衰变的情况下回填土有效扩散系数和阻滞因子的变化对于封闭屏障下方PCE蒸气稳态质量浓度没有影响，VOC蒸气稳态质量浓度均为9.23×10-4 μg/m3。对于污染源质量浓度不发生衰变的场地，回填土有效扩散系数和阻滞因子变化不影响场地中PCE蒸气风险的最终管控效果。
![]()
图 5 回填土有效扩散系数和阻滞因子对PCE蒸气质量浓度的影响Figure 5. Influences of effective diffusivity and retardation rate of back-filled soil on PCE vapor concentration2.3 原位土的影响
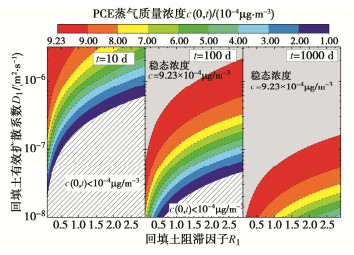
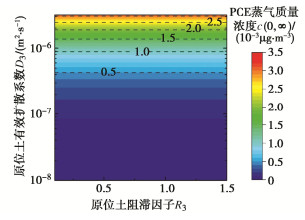
图 6为单层原位土有效扩散系数与阻滞因子对封闭屏障下方PCE蒸气质量浓度的影响。本算例中，HPRB上方的回填土选用砂土。由图 6可见，原位土有效扩散系数增加会导致封闭屏障下方PCE蒸气峰值质量浓度提高，而原位土阻滞因子变化不影响PCE蒸气峰值质量浓度。经计算，HPRB下方PCE蒸气入口通量与原位土有效扩散系数正相关，原位土有效扩散系数从10-8 m2/s增加至10-6 m2/s时，HPRB下方PCE蒸气稳态入口通量由1.45×10-6 g/(m2·s)增加至1.35×10-4 g/(m2·s)。HPRB下方入口通量低意味着PCE蒸气进入HPRB的速率缓慢，PCE蒸气在HPRB中反应更充分，所以HPRB的管控效果更好。对于污染源质量浓度不发生衰变的工况，HPRB更适用于原位土体有效扩散系数较低的污染场地。
![]()
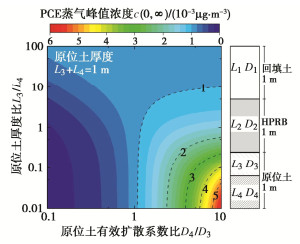
图 6 原位土有效扩散系数和阻滞因子对PCE蒸气质量浓度的影响Figure 6. Influences of effective diffusivity and retardation rate of local soil on PCE vapor concentration为考虑层状原位土对PCE蒸气迁移反应的影响，图 7展示了双层原位土相对厚度比与有效扩散系数比对PCE蒸气峰值质量浓度的影响。其中，原位土由第3层土和第4层土组成，总厚度为1.0 m，第4层土为均质砂土。随着第3层土的有效扩散系数D3增加，封闭屏障下方PCE蒸气峰值质量浓度提高，峰值质量浓度变化的范围与原位土的相对层厚有关。当L3等于L4时，D3增加2个数量级后封闭屏障下方PCE蒸气峰值质量浓度提高了800%。而当土层厚度L3低于原位土总厚度的2%时，D3增加2个数量级后封闭屏障下方PCE蒸气峰值质量浓度仅提高了20%，其影响相对较小。对于实际工程中，不同场地的原位土层的层数以及土层性质差异大，需要根据场地的实际情况具体分析。
![]()
图 7 原位土厚度比与有效扩散系数比对PCE蒸气质量浓度的影响Figure 7. Influences of layer thickness ratio and effective diffusivity ratio of local soil on PCE vapor concentration3. HPRB厚度与埋深的影响
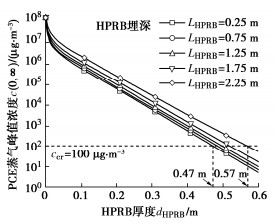
作为HPRB的关键设计参数，HPRB层的厚度dHPRB以及埋深LHPRB对封闭屏障下方PCE蒸气质量浓度的影响如图 8所示。本节算例中原位土体以及回填土都是均质砂土，污染源质量浓度保持恒定。当HPRB厚度小于0.01 m时，PCE蒸气峰值质量浓度随着HPRB厚度增加迅速降低。随着HPRB厚度继续增加，PCE蒸气峰值质量浓度呈现指数衰减趋势，增加HPRB厚度能够显著降低封闭屏障下方的PCE蒸气质量浓度。当HPRB埋深为0.25 m时，HPRB厚度大于0.47 m能满足封闭屏障下方的PCE蒸气峰值质量浓度低于给定的筛选值（100 μg/m3）。而当HPRB埋深为2.25 m时，HPRB厚度需大于0.57 m才能达到相同的管控效果。因此在HPRB埋深较浅时，HPRB厚度增加对PCE蒸气管控效果的提升更明显。
![]()
图 8 HPRB厚度与埋深对PCE蒸气质量浓度的影响.Figure 8. Influences of thickness and depth of HPRB on PCE vapor concentration图 9为HPRB埋深分别为1.0，1.5 m的两种工况下HPRB层两端的单位面积累计入口通量Fin和累计出口通量Fout随时间的变化。当HPRB厚度为0.5 m时，可以发现埋深为1.5 m工况的单位面积HPRB下方累计入口通量高于埋深为1 m的工况，这表明HPRB的下界面越靠近污染源，累计进入HPRB的PCE蒸气更多。虽然由于HPRB对PCE蒸气的氧化反应，更多的PCE蒸气在HPRB中被消耗，但是埋深为1.5 m的工况下单位面积HPRB上方的累计出口通量仍然比1 m埋深的工况更高。这表明更多的PCE蒸气穿过了HPRB，因此导致了HPRB埋深较大时封闭屏障下方PCE蒸气质量浓度更高。埋深过大的HPRB不仅会增加工程成本，还不利于对场地PCE蒸气风险的管控。
![]()
图 9 HPRB层埋深对HPRB两侧累计通量的影响Figure 9. Influences of depth of HPRB on PCE vapor accumulated influx rate and outflux rate of HPRB4. 污染源深度与衰减系数的影响
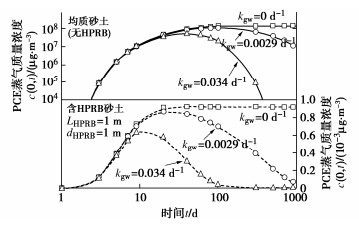
当考虑对场地中污染源进行修复或者考虑污染物在厌氧环境下的生物降解的情况，污染源处的蒸气质量浓度都会发生衰变。图 10为考虑不同污染源质量浓度衰减系数下均质砂土场地和铺设HPRB层的砂土场地中封闭屏障下方PCE蒸气质量浓度随时间的变化曲线。其中PCE污染源质量浓度的衰减系数分别取现有现场研究发现的最大值（0.034 d-1）、平均值（0.0029 d-1）和最小值（0 d-1）[20]。从图 10可以看出，无论是否铺设HPRB，污染源质量浓度的衰减都会导致封闭屏障下方PCE蒸气峰值质量浓度降低以及达到峰值质量浓度所需的时间减少。对于不含HPRB的均质砂土场地，不考虑污染源的质量浓度衰减会高估场地PCE蒸气逸出风险；而对于铺设了HPRB的砂土场地，不考虑污染源的质量浓度衰减会导致HPRB的保守设计，从而增加成本。因此，在进行场地污染物蒸气逸出风险评估以及HPRB设计前需要测定场地污染源质量浓度衰减系数。
![]()
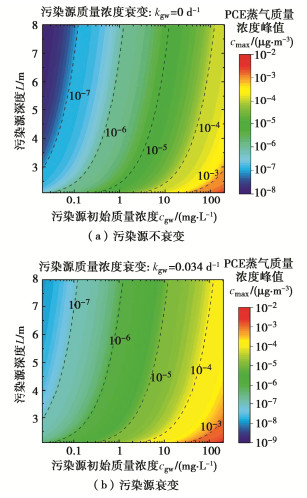
图 10 污染源衰减系数对PCE蒸气质量浓度的影响Figure 10. Influences of decay rate of source concentration on calculated PCE vapor concentration图 11为污染源质量质量浓度不发生衰变和发生衰变时污染源深度和初始质量质量浓度对封闭屏障下方PCE蒸气质量浓度峰值的影响。污染源初始质量浓度降低以及污染源深度增加都会导致封闭屏障下方PCE蒸气质量浓度峰值降低，污染源初始质量浓度和污染源深度对封闭屏障下方PCE蒸气质量浓度峰值的影响相互独立。不同的污染源初始质量浓度下，封闭屏障下方PCE蒸气质量浓度峰值随污染源深度增加而降低的比例是相同的。在污染源质量浓度不发生衰变的情况下，污染源深度从2.1 m增加至8.0 m会导致封闭屏障下方PCE蒸气质量浓度峰值降低超过1个数量级。而对于污染源质量浓度发生衰变的情况，污染源深度从2.1 m增加至8.0 m则会导致PCE蒸气质量浓度峰值降低超过2个数量级。因此，污染源质量浓度发生衰变的情况下污染源深度变化对封闭屏障下方PCE蒸气质量浓度峰值的影响比污染源质量浓度不发生衰变的情况大。
![]()
图 11 污染源初始质量浓度和污染源深度的影响Figure 11. Influences of initial concentration and depth of source on PCE vapor concentration5. HPRB设计思路
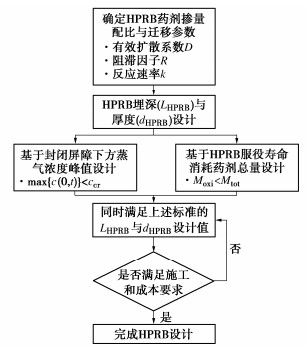
从前文的参数分析中可以发现，VOC蒸气在HPRB中的迁移参数和HPRB层的厚度及埋深都会对场地中VOC蒸气的管控效果有显著影响，因此在HPRB的设计过程中需要考虑这些因素的影响。本文提出HPRB的设计思路，其设计流程如图 12所示。
当确定污染场地需要采用HPRB对场地中的VOC蒸气污染进行管控后，首先需要通过室内试验对目标污染物在HPRB中的扩散系数、阻滞因子以及反应系数进行测定，优化HPRB层的药剂掺量配比以及含水率等材料参数。随后，需要根据场地土层条件对HPRB层的厚度dHPRB以及埋深LHPRB进行设计。dHPRB和LHPRB的设计需要满足如下两个条件：①封闭屏障下方的VOC蒸气质量浓度峰值小于土壤中VOC蒸气的质量浓度筛选值ccr；②在HPRB服役期间HPRB中药剂的累计消耗量Moxi小于HPRB中所包含的药剂总量Mtot。在同时满足上述两个条件后，需要考虑工程施工和成本要求，选取最适宜的设计参数组合。
基于上述HPRB设计思路，本文就美国环保署文件[22]中提到的一种粉砂互层土场地进行HPRB的模拟设计。该场地污染源埋深为8 m。场地土层自上而下分别是3 m砂土、1 m粉土、1 m砂土、1 m粉土和2 m砂土，土层参数见表 1。污染源VOC质量浓度cgw为200 mg/L，主要污染物类型为PCE；污染源质量浓度分别考虑发生衰减和不发生衰减两种情况，发生质量浓度衰减的情况下质量浓度衰减系数为0.0029 d-1。基于前人试验研究的结果，HPRB采用砂土和高锰酸钾固体1∶1配置，HPRB的孔隙参数如表 1所示，PCE蒸气在HPRB中的扩散系数和阻滞因子可通过式（4），（5）计算得到，PCE蒸气在HPRB中的二阶反应速率见表 2，HPRB上方的回填土采用原位砂土进行回填。
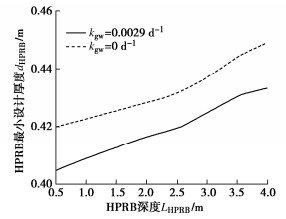
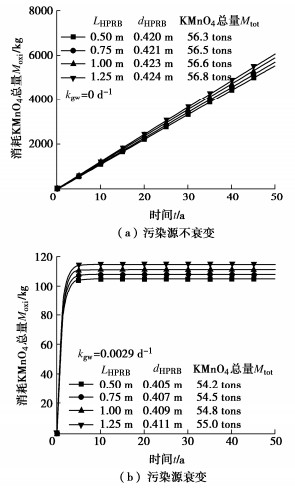
采用本文提出的解析模型能够计算出不同埋深HPRB下满足封闭屏障下方PCE蒸气质量浓度峰值小于筛选值（100 μg/m3）的HPRB最小设计厚度如图 13所示。选取50 a作为该场地HPRB的服役年限，分别取HPRB埋深为0.5，0.75，1，1.25 m 4种设计值所对应的HPRB最小设计厚度，能够计算出HPRB中高锰酸钾累计消耗总量随时间的变化如图 14所示。由图 14可以看出无论是否考虑污染源质量浓度发生衰变，各组设计值对应的50 a服役年限中高锰酸钾累计消耗量均小于HPRB层中所含有的高锰酸钾总量，因此各组设计值均满足先前给定的50 a服役寿命需求。考虑到工程中的开挖成本，该场地中的HPRB可以选用0.5 m埋深和0.405 m厚度作为考虑污染源衰变情况的设计参考值，选用0.5 m埋深和0.420 m厚度作为不考虑污染源质量浓度衰变情况的设计参考值。
![]()
图 13 HPRB深度与最小设计厚度设计曲线Figure 13. Design curves of depth and minimum thickness of HPRB6. 模型局限性
在HPRB长期服役过程中，HPRB的实际服役环境以及污染场地条件存在时空变异性，因此本文建立的解析模型也具有一定局限性。对于长期服役过程中地下水位发生季节性变化的工况，本文模型仅能考虑恒定的污染源深度，需要采用污染场地的历史最高水位作为最危险工况进行计算模拟，模型计算结果是偏保守的可能会导致HPRB的过度设计。对于原位土中含水率分布的空间差异的影响，虽然本模型假设各土层都是均匀介质，但是可根据不同深度处的含水率采用人为分层的方式进行模拟，这在已有的模型研究中有过应用[11]。但是对于本模型而言，层数过多一定程度上会影响计算效率，因此有必要进一步开展考虑土层含水率空间差异分布的模型研究。
7. 结论
本文提出了VOC蒸气在含有HPRB的层状土中迁移降解的一维瞬态解析模型。通过和数值模型的计算结果对比，验证了本文提出的解析模型正确性。随后，分析了场地中土层特性、HPRB埋深和厚度、污染源深度以及污染源质量浓度衰减系数等因素对VOC蒸气在土层中迁移的影响。最后在对VOC蒸气迁移规律分析的基础上，提出了HPRB埋深与厚度的设计思路，可为实际工程提供参考。本文主要得出以下4点结论。
（1）随着原位土扩散系数的降低，场地中VOC蒸气稳态质量浓度更低，HPRB更适用于原位土扩散系数较低的VOC污染场地。
（2）提高HPRB中氧化药剂和VOC蒸气的反应速率和HPRB饱和度都能够提升HPRB的服役性能；在高反应速率条件下，提升HPRB的饱和度效果更佳。
（3）HPRB埋深增加和厚度减小都会减弱HPRB对VOC蒸气的去除效果；在对HPRB进行设计时，需要综合考虑HPRB埋深以及厚度对封闭屏障下方VOC蒸气质量浓度以及氧化药剂累计消耗量的影响。
（4）污染源埋深增加和污染源初始质量浓度降低都会导致封闭屏障下方VOC蒸气质量浓度峰值降低；污染源质量浓度发生衰变会使VOC蒸气质量浓度峰值降低以及达到峰值所需的时间减小，因此需要对污染场地中污染源质量浓度衰减情况展开调查，避免HPRB的设计过度保守。
-
![]()
图 1 VOC蒸气在含HPRB土层中迁移概念模型图
Figure 1. Schematic graph of migration of VOC vapor in layered soil containing HPRB
![]()
图 2 本文模型计算结果与数值解对比
Figure 2. Comparison of results by proposed analytical model and numerical model
![]()
图 3 与均质土模型和现有HPRB模型计算结果对比
Figure 3. Comparison of results by proposed analytical model, homogeneous soil model and existing HPRB model
![]()
图 4 HPRB饱和度和反应速率对PCE蒸气质量浓度的影响
Figure 4. Influences of water saturation and reaction rate of HPRB on PCE vapor concentration
![]()
图 5 回填土有效扩散系数和阻滞因子对PCE蒸气质量浓度的影响
Figure 5. Influences of effective diffusivity and retardation rate of back-filled soil on PCE vapor concentration
![]()
图 6 原位土有效扩散系数和阻滞因子对PCE蒸气质量浓度的影响
Figure 6. Influences of effective diffusivity and retardation rate of local soil on PCE vapor concentration
![]()
图 7 原位土厚度比与有效扩散系数比对PCE蒸气质量浓度的影响
Figure 7. Influences of layer thickness ratio and effective diffusivity ratio of local soil on PCE vapor concentration
![]()
图 8 HPRB厚度与埋深对PCE蒸气质量浓度的影响.
Figure 8. Influences of thickness and depth of HPRB on PCE vapor concentration
![]()
图 9 HPRB层埋深对HPRB两侧累计通量的影响
Figure 9. Influences of depth of HPRB on PCE vapor accumulated influx rate and outflux rate of HPRB
![]()
图 10 污染源衰减系数对PCE蒸气质量浓度的影响
Figure 10. Influences of decay rate of source concentration on calculated PCE vapor concentration
![]()
图 11 污染源初始质量浓度和污染源深度的影响
Figure 11. Influences of initial concentration and depth of source on PCE vapor concentration
![]()
图 13 HPRB深度与最小设计厚度设计曲线
Figure 13. Design curves of depth and minimum thickness of HPRB
表 2 模型输入参数
Table 2 Input parameters used in simulation
土层有机碳含量foc[21]/(kg oc/kg soil) PCE分子量/(g·mol-1) Da[18]/(m2·s-1) Dw[18]/(m2·s-1) Hm[18] Koc[18]/(L·kg-1) 地下水VOC质量浓度cgw/(mg·L-1) 污染源衰变系数kgw[20]/d-1 二阶反应速率k”[19]/(M-1·s-1) coxi/(g·L-1) KMnO4分子量/(g·mol-1) 反应的化学计量比γ[8]/(kg KMnO4/kg PCE) 0.001 165.8 5.05×10-6 9.46×10-10 0.724 94.94 200 0~0.0029 0.0084 64 L 158 4/3 
下载: 导出CSV
-
[1] US Environmental Protection Agency. Petroleum Hydrocarbons and Chlorinated Solvents Differ in Their Potential for Vapor Intrusion[M]. Washington, DC: US Environmental Protection Agency, 2012.
[2] 刘惠, 陈奕. 有机污染土壤修复技术及案例研究[J]. 环境工程, 2015, 33(增刊1): 920-923. https://www.cnki.com.cn/Article/CJFDTOTAL-HJGC2015S1230.htm LIU Hui, CHEN Yi. Organic contaminated soil treatment technologies and remediation practices[J]. Environmental Engineering, 2015, 33(S1): 920-923. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HJGC2015S1230.htm
[3] 赵玲, 滕应, 骆永明. 我国有机氯农药场地污染现状与修复技术研究进展[J]. 土壤, 2018, 50(3): 435-445. https://www.cnki.com.cn/Article/CJFDTOTAL-TURA201803001.htm ZHAO Ling, TENG Ying, LUO Yongming. Status of organochlorine pesticide contaminated sites in China and advances in site remediation[J]. Soils, 2018, 50(3): 435-445. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TURA201803001.htm
[4] MAHMOODLU M G, HARTOG N, MAJID H S, et al. Oxidation of volatile organic vapours in air by solid potassium permanganate[J]. Chemosphere, 2013, 91(11): 1534-1538. doi: 10.1016/j.chemosphere.2012.12.035
[5] MAHMOODLU M G, HASSANIZADEH S M, HARTOG N, et al. Evaluation of a horizontal permeable reactive barrier for preventing upward diffusion of volatile organic compounds through the unsaturated zone[J]. Journal of Environmental Management, 2015, 163: 204-213.
[6] MAHMOODLU M G, HASSANIZADEH S M, HARTOG N, et al. Oxidation of trichloroethylene, toluene, and ethanol vapors by a partially saturated permeable reactive barrier[J]. Journal of Contaminant Hydrology, 2014, 164: 193-208. doi: 10.1016/j.jconhyd.2014.05.013
[7] ZINGARETTI D, VERGINELLI I, LUISETTO I, et al. Horizontal permeable reactive barriers with zero-valent iron for preventing upward diffusion of chlorinated solvent vapors in the unsaturated zone[J]. Journal of Contaminant Hydrology, 2020, 234: 103687. doi: 10.1016/j.jconhyd.2020.103687
[8] VERGINELLI I, CAPOBIANCO O, HARTOG N, et al. Analytical model for the design of in situ horizontal permeable reactive barriers (HPRBs) for the mitigation of chlorinated solvent vapors in the unsaturated zone[J]. Journal of Contaminant Hydrology, 2017, 197: 50-61. doi: 10.1016/j.jconhyd.2016.12.010
[9] YAO Y J, VERGINELLI I, SUUBERG E M. A two-dimensional analytical model of vapor intrusion involving vertical heterogeneity[J]. Water Resources Research, 2017, 53(5): 4499-4513. doi: 10.1002/2016WR020317
[10] FENG S J, ZHU Z W, CHEN H X, et al. Two-dimensional analytical solution for VOC vapor migration through layered soil laterally away from the edge of contaminant source[J]. Journal of Contaminant Hydrology, 2020, 233: 103664. doi: 10.1016/j.jconhyd.2020.103664
[11] FENG S J, ZHU Z W, CHEN H X, et al. Two-dimensional analytical solution for subsurface volatile organic compounds vapor diffusion from a point source in layered unsaturated zone[J]. Journal of Contaminant Hydrology, 2021, 243: 103916. doi: 10.1016/j.jconhyd.2021.103916
[12] XIE H J, WANG Q, BOUAZZA A, et al. Analytical model for vapour-phase VOCs transport in four-layered landfill composite cover systems[J]. Computers and Geotechnics, 2018, 101: 80-94. doi: 10.1016/j.compgeo.2018.04.021
[13] MILLINGTON R J, QUIRK J P. Permeability of porous solids[J]. Transactions of the Faraday Society, 1961, 57(0): 1200-1207.
[14] TALBOT A. The accurate numerical inversion of Laplace transforms[J]. IMA Journal of Applied Mathematics, 1979, 23(1): 97-120. doi: 10.1093/imamat/23.1.97
[15] MILLS W B, LIU S, RIGBY M C, et al. Time-variable simulation of soil vapor intrusion into a building with a combined crawl space and basement[J]. Environmental Science & Technology, 2007, 41(14): 4993-5001.
[16] DING X H, FENG, S J, ZHENG Q T, et al. A two-dimensional analytical model for organic contaminants transport in a transition layer-cutoff wall-aquifer system[J]. Computers and Geotechnics, 2020, 128: 103816.
[17] US Environmental Protection Agency. Vapor Intrusion Database[DB/OL]. Washington, DC: US Environmental Protection Agency (EPA), 2012. https://www.epa.gov/vaporintrusion/vapor-intrusion-database.
[18] US Environmental Protection Agency. Regional screening levels (RSLs)-generic tables[R/OL]. Washington, DC: US Environmental Protection Agency (EPA), 2021. https://www.epa.gov/risk/regional-screening-levels-rsls-generic-tables.
[19] WALDEMER R H, TRATNYEK P G. Kinetics of contaminant degradation by permanganate[J]. Environmental Science & Technology, 2006, 40(3): 1055-1061.
[20] ARONSON D, HOWARD P H. Anaerobic biodegradation of Organic Chemicals in Groundwater: A Summary of Field and Laboratory Studies[R]. North Syracuse: Environmental Science Center, Syracuse Research Corporation, 1997.
[21] ABREU L D V, JOHNSON P C. Simulating the effect of aerobic biodegradation on soil vapor intrusion into buildings: Influence of degradation rate, source concentration, and depth[J]. Environmental Science & Technology, 2006, 40(7): 2304-2315.
[22] US Environmental Protection Agency. Conceptual Model Scenarios for the Vapor Intrusion Pathway[R]. Washington, DC: US Environmental Protection Agency, 2012.
-
其他相关附件
计量
- 文章访问数: 262
- HTML全文浏览量: 50
- PDF下载量: 77
