Prediction model for TBM disc cutter wear based on dense core theory
-
摘要: CCS（Constant Cross Section）盘形滚刀磨损是影响硬岩隧道掘进工作效率和成本预算的关键问题。根据CCS型滚刀的工作特点和岩石切割破碎原理，分析研究滚刀破碎岩石的复杂应力状态，建立了考虑密实核效应的滚刀破岩机理。通过推导密实核长度的理论解析式，获得了基于塑性去除磨粒磨损机制的滚刀磨损量与法向荷载之间的数学关系式，进而提出了滚刀磨损速率及切削寿命预测模型。基于此，分析计算了深圳地铁12号线某区间共757环的正面滚刀实测磨损数据，发现预测值与实测值的相对差异率值均小于10%，验证了预测模型的有效性。此外，通过与现有滚刀磨损预测模型对比分析，结果表明本文提出的预测模型计算结果更接近于现场实测值，说明了滚刀磨损速率和切削寿命指标可作为评价滚刀磨损特性的可靠指标，为TBM工程现场刀具更换方案设计提供更为合理可行的理论依据。Abstract: The CCS (constant cross section) type disc cutter wear is an inevitably crucial puzzle that affects the construction efficiency and cost budgeting of hard rock excavation. In this paper, according to the working characteristics of the CCS type disc cutter and the theory of rock squeezing and cutting, the complex stress state of rock-breaking by the cutter is analyzed and the mechanism of disc cutter rock-breaking considering the dense core effect is established. By deducing theoretical analytical expressions of dense core length, the mathematical relationship between cutter wear amount and normal force based on the principle of plastic removal abrasiveness is obtained, then the prediction models for wear rate and the cutting life of a disc cutter are proposed. Based on this context, by analyzing and calculating the measured wear data of the front disc cutter of a total of 757 rings in a section of Metro Line 12 in Shenzhen, China, it is found that the relative difference rate between the predicted value and the measured value is less than 10%, which validates the reliability and accuracy of the prediction model. In addition, by comparing with an existing typical prediction model of the CCS type disc wear, the results show that the calculation results of the prediction model proposed in this paper are more consistent with the field measured values, indicating that the disc cutter wear rate and cutting life can be regarded as reliable indexes to evaluate the cutter wear characteristics, which provides a more reasonable and feasible theoretical basis for the design of tool replacement scheme in TBM engineering.
-
0. 引言
盘形滚刀作为TBM（Tunnel Boring Machine）破岩的核心关键部件，处于开挖设备最前端，直接暴露在岩石表面，通过与掌子面围岩之间发生一系列的复杂相互作用参与破岩掘进工作[1]。CCS（Constant Cross Section）盘形滚刀因具有破岩效率高、刀具磨损量小、比能耗低等优点，已广泛应用于几乎所有坚硬岩石开挖项目[2]。然而，由于硬岩突出的高强度和高磨蚀性，滚刀磨损已成为TBM施工过程中不可避免的关键性难题。据报道，对于长距离TBM硬岩隧道开挖项目，因滚刀磨损导致的刀具费用约占施工费用的1/3[3]。此外，若不及时更换过度磨损的刀具，刀盘会产生过大的旋转载荷，甚至会卡死，这不仅会降低挖掘效率，而且容易引发施工潜在风险[4]。因此，建立合理准确的CCS盘形滚刀磨损预测模型对提高TBM掘进效率及经济性具有重要意义。
滚刀磨损是一个包含挤压、剪切及摩擦等多种荷载作用的复杂过程，主要受岩体类型及力学性能、矿物硬度、掘进参数、刀具材料及荷载分布规律等因素影响[5]。针对硬岩盘形滚刀磨损预测问题，国内外学者开展了大量的研究工作。20世纪90年代，美国科罗拉多矿业学院（CSM）[6]提出了使用磨蚀性指数（CAI）来预测滚刀寿命的CSM模型。挪威理工学院[7]建立了基于挪威磨损值（SJ，AVS）的刀具寿命指数（CLI）预估模型。魏南珍等[8]根据秦岭隧道的工程数据，提出了不同区域盘形刀具累积磨损量和更换频率的计算模型。20世纪初，张照煌等[9]通过盘形滚刀破岩理论分析，认为滚刀刀刃破岩点弧长与磨损量存在正比例关系。Frenzel[10]基于CAI和工程数据分析提出了一套滚刀消耗预测模型。Hassanpour等[11]根据伊朗Karaj输水隧洞的数据建立了基于岩石硬度和单轴抗压强度的滚刀寿命预测公式。随后，李刚等[12]开发了基于CSM模型Rostami公式的CCS盘形滚刀破岩受力理论计算模型。在此基础上，杨延栋等[13]、吴俊等[14]和Sun等[15]基于麻省理工学院Rabinowicz提出的微观磨粒磨损机制，建立了盘形滚刀磨损预测模型并进行了验证。表 1列出了国内外现有典型的盘形滚刀磨损预测模型。
表 1 国内外现有典型的盘形滚刀磨损预测模型Table 1. Existing domestic and foreign typical disc cutter wear prediction models预测模型 原理或方法 公式 数据范围 应用情况 CSM[6] 岩石挤压与剪切破坏理论、LCM试验 $ {F_{\text{V}}} = 8.76{T^{0.797}}{R^{0.788}}{\varphi ^{0.602}}{S^{0.28}}\sigma _{\text{c}}^{{\text{0}}{\text{.629}}}\sigma _{\text{t}}^{{\text{0}}{\text{.195}}} $ — 完整性较好的玄武岩、石灰岩、花岗岩 NTNU[7] 挪威磨蚀性试验(SJ、AVS) $ {H_{\text{f}}} = \frac{{{\text{π }}{D^2} \cdot {H_0} \cdot {k_i} \cdot PR}}{{4N}} $ 超过250 km隧道 花岗岩、凝灰岩 魏南珍等[8] 现场磨损数据拟合 $ M = 0.0229R_i^2 + 2431{R_i} - 3.2245 $ 约3.7 km秦岭隧道 混合花岗岩和混合片麻岩 张照煌等[9] 岩石挤压、剪切及张拉破坏理论 $ {F_{\text{V}}} = \frac{{KA}}{{P_{\text{f}}^2}} \cdot P $ 约5.6 km秦岭隧道 完整性较好的混合花岗岩 Frenzel等[10] Cerchar磨蚀性试验(CAI) $ {H_{\text{f}}} = \frac{{{\text{π }}{D^2}}}{4} \cdot \frac{{n \cdot P}}{{1000}} \cdot \frac{{2S}}{{D \cdot 1000}} $ 超过127 km隧道 微风化花岗岩 Hassanpour等[11] 岩石硬度试验(VHNR) $ {H_{\text{f}}} = - 2.669{\text{VHNR}} - 7.891{\text{UCS}} + 3430.955 $ 约30 km长Karaj输水隧洞 弱风化火山岩 李刚等[12] CSM模型 $ {F_{\text{t}}} = \frac{{TR\phi {P_{\text{r}}}}}{{1{\text{ + }}\psi }} $, $ {P_{\text{r}}} = C \cdot {(\frac{{S\sigma _{\text{c}}^{\text{2}}{\sigma _{\text{t}}}}}{{\varphi \sqrt {RT} }})^{1/3}} $ 约18.5 km秦岭隧道 完整较好的玄武岩、石灰岩、花岗岩 杨延栋等[13] Rabinowicz微切削原理 $\omega = 0.16{K_{\text{s}}}\frac{{{S^{\frac{1}{3}}}{R_i}{\sigma _{\text{c}}}}}{{{D_0}{T^{\frac{1}{6}}}{h^{\frac{1}{6}}}{\sigma _s}}}$ 约2 km狮子洋隧道和531 m广州地铁隧道 微风化混合花岗岩 注：Fv为滚刀法向垂直力（N），Hf为滚刀基本寿命（m3/cutter），M为滚刀径向磨损量（mm），Ft为滚刀法向和切向合力（N）。 然而，上述现有滚刀磨损预测模型在实际工程应用时，仍存在以下问题：①由于滚刀破岩磨损机理具有复杂性和多样性，目前研究者针对盘形滚刀破岩的复杂应力状态尚无明确的定义。②现有滚刀破岩磨损预测公式大多基于单一较完整的岩石建立，忽虑了岩体类型及节理性质对破岩效果的影响。③鲜少有研究基于现场实际工程数据验证理论公式，导致已提出的预测模型实际应用性不足。针对上述问题，本文通过分析研究盘形滚刀破碎岩石的复杂应力状态，建立考虑密实核效应的滚刀破岩多阶段复杂过程，提出一种更具可靠性和准确性的硬岩TBM盘形滚刀磨损预测模型。同时，利用实际工程数据验证了模型的可靠性与准确性。
1. 密实核破岩机理分析
从宏观角度来看，TBM在开挖掘进过程中，盘形滚刀与接触岩石主要通过发生滚刀侵入挤压和剪切作用形成岩片[16]。另一方面，以往研究结果表明，在滚刀压头作用下，岩石未达到完全破碎前，在压头侵入前方出现已被粉碎的或显著塑性变形的物体，称为密实核，一般外形呈球形或半球形。假设密实核处于静水压力状态，则其内部3向主应力相等。根据弹塑性力学理论可知，静水压力不影响屈服强度，只产生体积变形。但是由于岩石结构的非均质性以及内部应力分布的非均匀性，则导致岩石内部仍然会发生破坏[17-18]。此外，密实核是岩石破碎体的一部分，也是决定岩石破碎条件及效率的关键因素。
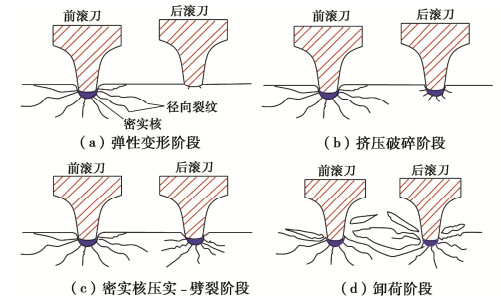
以往刀具破岩机理的研究过程中，引人注意的是，余静[17]根据大量的大理岩、石灰岩和花岗岩破碎试验，提出密实核是机械破岩过程中普遍存在的现象，并把岩石破碎分成变形、裂纹源出现、密实核形成、密实核储能、径向裂纹和粉劈以及卸载等6个阶段。随后，孙伟等[18]和Huo等[19]认为密实核内部为静水压力特性，将滚刀破岩过程分为弹性变形阶段、挤压破碎阶段、密实核破碎阶段与卸载阶段4个阶段。此外，张桂菊等[20]通过分析滚刀破岩能量传递机制，发现岩石内部裂纹的扩展是导致岩石失效的主要原因。基于此，本文针对特定的岩石条件，考虑到盘形滚刀破碎岩石的复杂应力状态及密实核效应，在以往研究[17-20]基础上将岩石破碎过程划分为4个主要阶段：弹性变形阶段、挤压破碎阶段、密实核压实-劈裂阶段和卸荷阶段，每个阶段的发展及演化过程如图 1所示。具体阐述为：在弹性变形阶段，由于岩石的受力没有超过屈服强度极限，则属于弹性变形，岩石表面出现略微凹陷现象；针对挤压破碎阶段，滚刀下方接触岩石的受力超过抗压强度，裂纹开始产生并不断扩展，导致岩石破碎，最终形成破碎带；随着滚刀载荷的不断增大和周围裂纹的交汇，刀刃下方破碎区的岩粉被压实，形成近似半球体的密实核。当密实核中储存的能量达到极限时，周围岩石因承受荷载超过抗拉强度产生径向裂纹。由于滚刀尖端的应力不断集中，导致微裂纹失稳并扩展。最后，当相邻滚刀间距满足一定条件时，长裂纹因受到粉楔作用一方面可扩展至自由面，发展形成块岩；另一方面相邻长裂纹被滚刀贯穿，岩石发生劈裂破碎。当刀盘突然卸载时，储存在岩石内部和密实核的能量被释放，岩石碎片从坑中排出，完成一次完整的破岩过程。
2. CCS型滚刀磨损预测模型建立
大量工程实践[15]表明，均匀磨损是导致盘形滚刀磨损的主要原因，约占总数的80%~90%。因此，有必要对正面盘形滚刀磨损进行评估和预测，为制定可靠的换刀计划和准确估算刀耗成本提供必要的依据。为了建立合理可靠的盘形刀具磨损预测模型，需要确定其磨损机理和性能。
2.1 塑性去除磨粒磨损机制
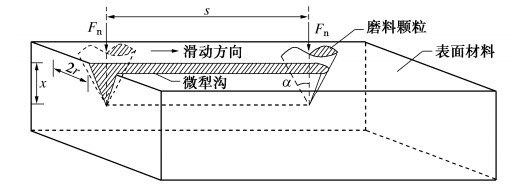
根据圆盘刀具磨损实验室试验结果[21]，均匀磨损的主要原因是塑性去除磨粒磨损，磨粒磨损约占总磨损的82.9%。虽然岩石的硬度和强度一般低于刀环，但一些硬度较高的矿物，如石英，可以穿透刀环表面，变成磨粒，最终导致刀圈表面材料发生磨粒磨损。为定量地描述和分析不同硬度材料的研磨性，Rabinowicz[22]利用微观切削假说原理，假定将磨粒看成硬质颗粒圆锥体，建立了磨料磨损简化模型。在以往滚刀磨损研究方面，部分学者利用该模型取得了可靠的研究成果。
如图 2示，假设接触面上磨粒有N个微凸体，则磨粒承受法向载荷${F_{\text{n}}}$为
$$ {F_{\text{n}}} = N\frac{{{\text{π }}{r^2}}}{2}{\sigma _{\text{s}}}\text{，} $$ (1) $$ N = \frac{{2{F_n}}}{{{\text{π }}{r^2}{\sigma _{\text{s}}}}}\text{，} $$ (2) ![]()
图 2 基于塑性去除机制的磨粒磨损示意图Figure 2. Schematic diagram of abrasiveness based on plastic removal mechanism式中，${F_{\text{n}}}$为磨粒承受法向载荷（kN），r为锥底半径，则犁出的沟槽宽度为2r（m），${\sigma _{\text{s}}}$为被磨损材料的屈服强度（MPa）。当磨粒压入深度为x，滑动距离为s时，则V0可表示为
$$ {V_0} = N \times rx = \frac{{2{F_{\text{n}}}}}{{{\text{π }}{r^2}{\sigma _{\text{s}}}}} \times r \times \frac{r}{{\tan \alpha }} = \frac{{2{F_{\text{n}}}}}{{{\text{π }}{\sigma _{\text{s}}}\tan \alpha }}\text{，} $$ (3) 式中，V0为单位滑动距离下的微犁沟体积，即为磨损体积（m3），$\alpha $为圆锥体半角（rad）。考虑到微凸体相互作用后可以产生磨损碎屑的比例分数记为K，则式（3）可转化为
$$ {V_0} = K\frac{2}{{\tan \alpha }} \times \frac{{{F_{\text{n}}}}}{{{\text{π }}{\sigma _{\text{s}}}}} = {K_{\text{s}}}\frac{{{F_{\text{n}}}}}{{{\text{π }}{\sigma _{\text{s}}}}}\text{，} $$ (4) 式中，Ks为磨粒磨损系数, 与磨粒硬度、形状尺寸、磨损形式以及起切削作用的磨粒数量等因素有关，一般可根据试验获取。Rabinowicz等[23]认为钢材之间的三体磨损磨粒尺寸约为80 μm，Ks取值为4×10-3。式（4）说明了磨粒磨损体积与法向荷载成正比例关系。换句话讲，定量分析滚刀磨损体积的核心任务是求解滚刀法向荷载值。
2.2 滚刀法向荷载推导
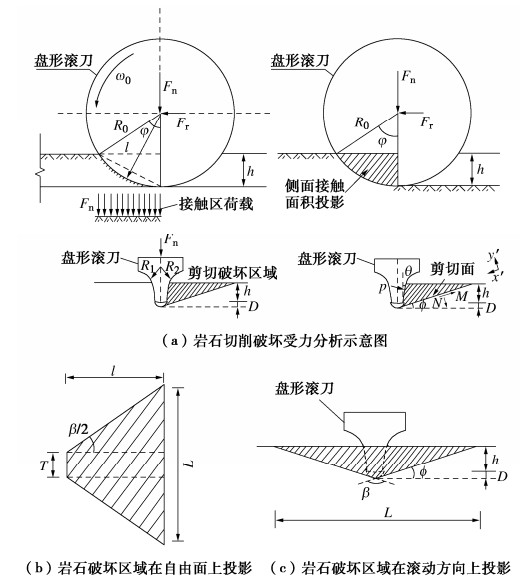
以往研究结果表明[24]，科罗多拉矿业学院提出的近似常截面接触的滚刀CSM受力分析模型最为经典，且应用较广泛。但该模型是基于完整岩石线性切割试验数据建立，忽虑了岩体类型及节理性质对破岩过程的影响，计算结果常与实际测量值存在明显差异。此外，也有部分学者根据滚刀压痕试验和小尺寸岩石破碎试验共性规律，提出了针对于CCS盘形滚刀的受力模型，但往往忽虑了密实核的破岩作用，这显然与实际情况不符[25]。为解决此问题，本文基于建立的密实核破岩机理，提出一种考虑密实核效应的CCS盘形滚刀切削破岩理论模型，如图 3所示。
如图 3（a）所示，由于密实核主要在刀刃正下方破碎区域形成并被压实，则假定密实核为半椭球型，长度为D。根据莫尔−库仑破坏准则，假设岩石属于剪切破坏，破碎面受到压应力$ \sigma $和剪切应力τ共同作用。由力学平衡原理可知，滚刀法向力Fn可分解为垂直滚刀刃面上的分力R1，R2，以及传递给密实核的分力Q。由于滚刀单次破岩周期内的侵入深度较小，因此不考虑刀刃侧面的摩擦力[26]。刀刃侧面分力R1在剪切断裂面上形成剪切力M和法向力N。当剪应力τ超过黏聚力c和内摩擦力$\sigma \tan \alpha $时，便发生剪切破碎。即破坏条件为
$$ \tau = c + \sigma \tan \alpha 。 $$ (5) 式中$ \tau $为剪切面上的剪应力（Pa）；$\sigma $为剪切面上的正应力（Pa）；α为岩石的内摩擦角（rad）；c为岩石的黏聚力（Pa）。因此，以单位滚刀刃长为研究对象，根据剪切破碎面的受力平衡分析可得
$$ \left.\begin{array}{l}\frac{ph}{\mathrm{cos}\theta }\mathrm{cos}(\theta +\varphi )=\frac{\tau (h\text{+}D)}{\mathrm{sin}\varphi }\text{ }\text{，}\\ \frac{ph}{\mathrm{cos}\theta }\mathrm{sin}(\theta +\varphi )=\frac{\sigma (h\text{+}D)}{\mathrm{sin}\varphi }\text{ }。\end{array}\right\} $$ (6) 式中R0为圆盘刀具半径（m）；T为刀刃宽度（m）；h为刀具侵入岩石深度（m/rev）；p为刀刃侧面与岩石接触区域任意点的应力值（Pa）；θ为刀刃倾角（rad）；ϕ为剪切面与水平面的夹角（rad）。将式（6）代入式（5）可得
$$ \tau - \sigma \tan \alpha = \frac{{ph\sin \phi \cos (\phi + \theta + \alpha )}}{{(h{\text{ + }}D)\cos \theta \cos \alpha }} = c \text{，} $$ (7) 式中，τ -σtanα为ϕ的函数，因此，令式（7）对ϕ的一次导数为零，即可得
$$ \phi = \frac{{\text{π }}}{{\text{4}}} - \frac{{\theta + \alpha }}{2} 。 $$ (8) 由式（8）可知，剪切面发生在倾角为$ \left( {\frac{{\text{π }}}{4} - \frac{{\theta + \alpha }}{2}} \right) $的平面上。当$ \theta + \alpha $ < 90°时，岩石可发生剪切破碎，将式（8）代入式（7）可求解p，
$$ p = \frac{{2c(h + D)\cos \theta \cos \alpha }}{{h\left[ {1 - \sin (\theta + \alpha )} \right]}} 。 $$ (9) 假设岩石发生剪切破碎时，密实核附近各向应力都满足岩石抗破碎强度，那么就有p=$ {\sigma _{\text{c}}} $ [27]，则密实核的长度为
$$ D = \frac{{{\sigma _{\text{c}}}h\left[ {1 - \sin (\theta + \alpha )} \right]}}{{2c\cos \theta \cos \alpha }} - h 。 $$ (10) 在图 3（b）中，根据压头侵入试验线性规律，假设CCS型盘形滚刀破岩为半无限体侵入过程，则认为破岩所需推力$ {F_{\text{n}}} $与岩石破碎坑在自由面形成的破碎面积A成正比[26]，其基本理论公式为
$$ {F_{\text{n}}} = A{\sigma _{\text{n}}} \text{，} $$ (11) 式中，$ {\sigma _{\text{n}}} $为比例系数，定义为滚刀压入强度，它与岩石单轴抗压强度$ {\sigma _{\text{c}}} $有关，
$$ {K_{\text{n}}} = \frac{{{\sigma _{\text{n}}}}}{{{\sigma _{\text{c}}}}} \text{，} $$ (12) 式中，Kn为滚压系数，考虑了岩体类型及节理性质，可以根据滚压试验确定其数值。一般情况下，Kn=0.47~0.7，大理岩为0.53，花岗岩为0.7，有水平层理的石灰岩为0.43，节理较发育的软岩Kn值偏小，完整性较好的硬岩Kn偏大[26]。实际上，滚刀与岩石破碎坑在自由面形成的破碎面积A为不规则图形，但与岩石破碎角β密切相关，β+2ϕ=π。为简化滚刀破岩力计算模型，做以下假设：①岩石发生阶跃破碎前，滚刀推力与接触面积存在线性关系；②贯入度值相对滚刀半径很小，假设破碎坑区域各向应力值相同；③滚刀与岩石接触自由面投影近似梯形。因此，A可由下式表示：
$$ A=\frac{1}{2}(L+T) \sqrt{R_{0}^{2}-\left(R_{0}-h\right)^{2}} 。 $$ (13) 此外，根据图 3(c)中几何关系可得到剪切破碎坑长度L为
$$ L = 2(h + D)\tan \frac{\beta }{2} 。 $$ (14) 将式（12）~（14）代入式（11）中可得
$$ {F_{\text{n}}} = \frac{1}{2}{K_{\text{n}}}{\sigma _{\text{c}}}\left[ {T + 2(h + D)\tan \frac{\beta }{2}} \right]\sqrt {R_0^2 - {{({R_0} - h)}^2}} 。 $$ (15) 由式（15）可以看出，滚刀法向荷载不仅与滚刀几何参数、掘进参数及岩石性质相关，还与密实核长度D密切相关，这也符合文献[26]的研究观点。此外，式（15）也反映了密实核是滚刀破岩过程中的重要几何参数，直接影响岩石破碎体积及滚刀荷载分布规律。
2.3 滚刀磨损速率ω建立
现场评价滚刀磨损程度是极为重要的任务，但目前尚没有统一的衡量标准。本文基于塑性去除磨粒磨损机制，引入考虑密实核破岩效应的滚刀法向力解析式，建立一种可靠的CCS型刃盘形滚刀磨损预测模型。当滚刀沿着刀盘旋转时，滚刀上破岩点的切削路径是以滚刀安装半径Ri为半径和贯入度h为导程的圆柱螺旋线。由图 3（a）可知，滚刀磨损只发生在滚刀前进方向滚刀与岩石接触的弧线上，则滚刀转动1圈的实际总切削路径可近似为弦长l：
$$ l = {R_0}\varphi \approx \sqrt {2{R_0}h} 。 $$ (16) 通常工程师在现场测量的滚刀磨损值为滚刀径向磨损长度，因此，本文提出滚刀径向磨损深度m的概念，
$$ m = \frac{V}{{2{\text{π }}{R_0}T}}{\text{ = }}\frac{{{V_0}l}}{{2{\text{π }}{R_0}T}}。 $$ (17) 为了定量评价滚刀磨损快慢程度，调整现场掘进参数，特别地建立滚刀磨损速率指数ω，定义为TBM掘进单位距离滚刀径向累计磨损长度。联立式（4），（15）~（17），则ω表示为
$$\omega = \frac{M}{L} = \frac{{m{R_i}}}{{h{R_0}}}\\ = \frac{{{K_{\text{s}}}{K_{\text{n}}}{\sigma _{\text{c}}}{R_i}\sqrt {R_0^2 - {{({R_0} - h)}^2}} }}{{2{{\text{π }}^2}T{\sigma _{\text{s}}}\sqrt {2R_0^3h} }}\left[ {T + 2(h + D)\tan \frac{\beta }{2}} \right] \text{，} $$ (18) 式中，L为TBM掘进距离，M为TBM掘进L距离滚刀的径向累计磨损长度。由于硬岩掘进实际过程中贯入度h与滚刀半径R0相差极大，因此，2R0−h ≈ D0，D0为滚刀直径，则式（18）可简化为
$$ \omega = \frac{{{K_{\text{s}}}{K_{\text{n}}}{\sigma _{\text{c}}}{R_i}}}{{{{\text{π }}^2}T{\sigma _{\text{s}}}{D_0}}}\left[ {T + 2(h + D)\tan \frac{\beta }{2}} \right] 。 $$ (19) 2.4 滚刀寿命指数$ \lambda $建立
现场滚刀的耐磨性评价也尤显重要，直接影响着刀具更换时机与换刀方案。科研人员通常采用滚刀寿命指数来表征滚刀耐磨性，其反映了单把圆形滚刀正常工作条件下的最大切削路径[7]。基于此，为了定量评估滚刀耐磨蚀性能，本文建立滚刀切削寿命指数$ \lambda $，定义为盘形滚刀在正常允许磨损量[δ]下的最大切削路径，则$ \lambda $表示为
$$ \lambda = \frac{{\left[ \delta \right]}}{\omega } = \frac{{{{\text{π }}^2}T{\sigma _{\text{s}}}{D_0}\left[ \delta \right]}}{{{K_{\text{s}}}{K_{\text{n}}}{\sigma _{\text{c}}}{R_i}\left[ {T + 2(h + D)\tan \frac{\beta }{2}} \right]}} 。 $$ (20) 3. 工程实例验证
3.1 工程概况及计算参数
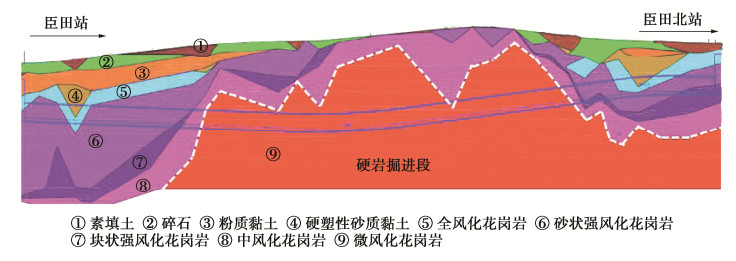
深圳地铁12号线臣田站—臣田北站区间（简称：臣臣区间）全线长为1040.826 m，隧道为单洞双线设计，采用2台海瑞克$ \phi $6470 mm复合式土压平衡盾构机开挖，具体技术参数见表 2，其中刀盘布置和刀盘区域划分如图 4所示。图 5为该区间隧道地质剖面图，隧道主要穿越微风化花岗岩地层，全断面硬岩左线长度约539 m、右线长约600 m，占区间开挖长度的52%和60%，岩石单轴抗压强度为68.5~168.3 MPa。由于硬岩区间岩石的高强度和高磨蚀性，导致刀具磨损及更换频率问题极为突出。
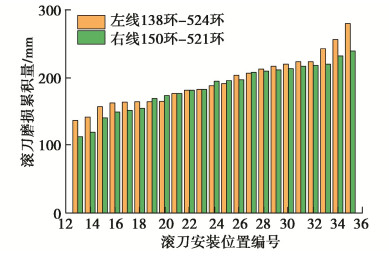
表 2 复合式土压平衡盾构机技术参数Table 2. Technical parameters of composite EPB shield machine参数 整机功率/kW 刀盘转速/(r·min-1) 扭矩/(kN·m) 推力/kN 推进速度/(mm·min-1) 刀盘开口率/% 滚刀数量/把 计算值 1668.05 1.8 2300 10000 15 35 41 参数 中心滚刀数量/把 正面滚刀数量/把 边滚刀数量/把 滚刀直径/mm 刀刃宽度/mm 刀刃角/(°) 刀圈硬度/HRC 计算值 6 23 12 457 19 20 60 ![]()
图 4 刀盘布置和刀盘区域划分示意图Figure 4. Schematic diagram of cutterhead layout and cutterhead area division为验证盘形滚刀磨损预测模型，选取臣臣区间左线138环—524环与右线150环—521环开挖掘进段作为研究对象，分析整理该掘进段的相关掘进参数、岩石力学指标及滚刀磨损数据。由于选取的左右线开挖掘进段相邻较近且均在微风化花岗岩硬岩区间，依据现场实际掘进情况取h为0.008 m/rev。通过对刀具进行硬度试验，得出滚刀刀刃的硬度值为60 HRC，根据国家标准《黑色金属硬度及强度换算值》（GB/T1172—1999）可换算出刀圈屈服强度${\sigma _{\text{s}}}$=1587 MPa。此外，依据《工程岩体试验方法》（GB/T 50266—2013）开展相应室内试验可获得岩石力学相关指标，见表 3。正面滚刀累计磨损量如图 6示，[${\sigma _{\text{s}}}$]=20 mm。
表 3 微风化花岗岩力学性质及计算参数Table 3. Mechanical properties and calculation parameters of slightly weathered granulated granite参数 密度/(kg·m-3) 抗压强度/MPa 抗拉强度/MPa 黏聚力/MPa 内摩擦角/(°) 弹性模量/GPa 泊松比 完整性系Kv 滚压系Kn 计算值 2700 90 6.89 20.8 42.5 26.7 0.22 0.55 0.7 3.2 滚刀磨损速率
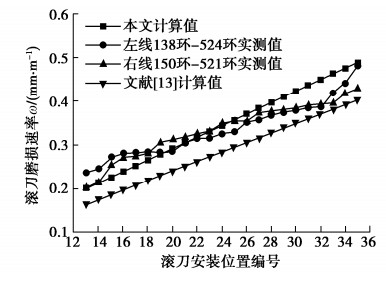
基于上述左右线开挖掘进段的相关统计参数，对式（19）中的滚刀径向磨损速率ω进行验证。以正面滚刀的实际累计磨损量M除以掘进距离L计算得到结果作为滚刀磨损速率实测值ω1；通过式（11）计算得到的结果作为滚刀磨损速率计算值ω2。为评估本文建立的CCS盘形滚刀磨损速率预测模型的可靠性，将计算值ω2与实测值ω1之间的相对差异率记为ξω，
$$ {\xi _\omega } = \left| {\frac{{{\omega _2} - {\omega _1}}}{{{\omega _1}}}} \right| \times 100{\text{% }}。 $$ (21) 图 7为盘形滚刀磨损速率指标计算结果。由图 7可知，由于研究区间地层条件及刀具设计参数的特殊性，左、右线掘进区间滚刀的磨损速率变化趋势基本一致，实测值和计算值均随着滚刀安装半径增加呈增大趋势，且滚刀磨损速率实测值基本稳定在计算值附近。很显然，部分实测值波动较大意味着该位置的滚刀很大可能发生了异常磨损。此外，可以看出理论计算值略大于实测值，这主要是因为式（19）选取了岩石抗压强度的平均值作为输入参数，忽虑了岩石参数的各向异性，导致结果偏大。值得注意的是，左、右线掘进区间滚刀磨损速率计算值与实测值的平均差异率分别为8.5%和7.2%，均小于10%，说明了理论计算模型在工程应用上具有可靠性和准确性。因此，滚刀磨损速率指数ω可作为评价现场滚刀磨损快慢程度的重要指标。
![]()
图 7 滚刀磨损速率预测模型验证及对比Figure 7. Validation and comparison of prediction models for cutter wear rate3.3 滚刀切削寿命
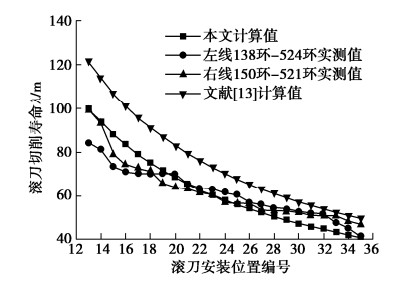
根据式（20）可分别计算得到滚刀切削寿命实测值λ1与计算值${\lambda _2}$，同样，为了评估本文建立CCS盘形滚刀寿命预测模型的可靠性，定义${\xi _\lambda }$表示计算值${\lambda _2}$与实测值${\lambda _1}$之间的相对误差。滚刀磨损寿命指数验证结果如图 8所示。由图 8可以看出，左、右线掘进区间的正滚刀切削寿命指数变化趋势总体一致，实测值在计算值附近波动，且随着滚刀安装半径增加呈幂函数减小趋势。此外，滚刀切削寿命理论计算平均值为62.3 m，左、右线实测平均值分别为61.7，62.4 m，且其平均相对差异率分别为8.6%和6.9%，均小于10%，这说明理论计算与实测结果基本一致，意味着理论计算模型具有可靠性和准确性。因此，滚刀寿命指数λ可作为现场滚刀更换方案的重要衡量指标。
![]()
图 8 滚刀切削寿命预测模型验证及对比Figure 8. Validation and comparison of prediction models for cutter cutting life3.4 模型对比分析
由表 1可知，与其他现有典型模型相比，文献[13]是基于微切削磨粒磨损机理，通过建立滚刀磨损体积与CSM模型法向荷载的相关性，提出了正面盘形滚刀磨损速率预测模型，具有一定的理论和试验依据。因此，为进一步验证本文提出的盘形滚刀磨损预测模型的合理性和可靠性，将该模型与文献[13]提出的模型进行对比分析。根据表 2，3中的计算参数，可以获得文献[13]中相应的正面滚刀磨损速率及切削寿命计算值，结果分别如图 7，8所示。从图 7，8可以看出，本文建立的滚刀磨损速率与切削寿命的理论分析结果与文献[13]计算值随安装半径增大呈现出类似的变化趋势。通过对比发现，本文的预测模型分析结果更接近于现场实测值，且平均相对差异率明显小于文献[13]，而文献[13]的磨损速率计算结果偏小。很显然，造成这些差别的主要原因是由于文献[13]提出的模型一方面忽虑了密实核效应在滚刀破岩过程中的作用，另一方面则是没有表征岩体类型及节理特性对滚刀磨损过程的影响，导致其整体磨损量较小。因此，可以推断出本文提出的盘形滚刀磨损预测模型更具有合理性和有效性。此外，限于工程现场试验条件，后续有待开展更多不同岩体类型、节理及力学特性的案例研究以进一步验证。
4. 结论
（1）根据盘形滚刀的工作特点和岩石切割破碎原理，分析研究盘形滚刀破碎岩石的复杂应力状态，建立了考虑密实核效应的滚刀破岩多阶段复杂过程，认为滚刀破岩可主要分为弹性变形阶段、挤压破碎阶段、密实核压实–劈裂阶段和卸荷阶段。
（2）基于莫尔库仑岩石破坏准则，推导了密实核长度的理论解析式，建立了基于塑性去除磨粒磨损机制的滚刀磨损量与法向荷载之间的数学关系式。从滚刀运动学角度定义并推导了滚刀径向磨损速率及切削寿命指数，进而提出了适用于CCS型刃的盘形滚刀磨损预测模型。
（3）选取深圳地铁12号线臣田站—臣田北站左线138—524环和右线150—521环硬岩区间正面滚刀磨损数据，分别与理论预测模型预测值进行比较，发现预测值与实测值基本一致且关联性较好。此外，左、右线滚刀磨损率的平均相对差异率值分别为8.5%，7.2%，以及切削寿命分别为8.6%，6.9%，均小于10%，验证了预测模型的有效性及准确性。
（4）通过与现有典型滚刀磨损预测模型对比分析，结果表明本文的预测模型计算结果更接近于现场实测值，说明提出的滚刀磨损速率和切削寿命指标可作为指导TBM工程现场滚刀更换方案的可靠性指标。限于现场试验条件，预计合作者将提供更多的工程案例以扩充数据库，进一步提高本文所建立预测模型的可靠性和通用性。
-
![]()
图 2 基于塑性去除机制的磨粒磨损示意图
Figure 2. Schematic diagram of abrasiveness based on plastic removal mechanism
![]()
图 4 刀盘布置和刀盘区域划分示意图
Figure 4. Schematic diagram of cutterhead layout and cutterhead area division
![]()
图 7 滚刀磨损速率预测模型验证及对比
Figure 7. Validation and comparison of prediction models for cutter wear rate
![]()
图 8 滚刀切削寿命预测模型验证及对比
Figure 8. Validation and comparison of prediction models for cutter cutting life
表 1 国内外现有典型的盘形滚刀磨损预测模型
Table 1 Existing domestic and foreign typical disc cutter wear prediction models
预测模型 原理或方法 公式 数据范围 应用情况 CSM[6] 岩石挤压与剪切破坏理论、LCM试验 FV=8.76T0.797R0.788φ0.602S0.28σ0.629cσ0.195t — 完整性较好的玄武岩、石灰岩、花岗岩 NTNU[7] 挪威磨蚀性试验(SJ、AVS) Hf=π D2⋅H0⋅ki⋅PR4N 超过250 km隧道 花岗岩、凝灰岩 魏南珍等[8] 现场磨损数据拟合 M=0.0229R2i+2431Ri−3.2245 约3.7 km秦岭隧道 混合花岗岩和混合片麻岩 张照煌等[9] 岩石挤压、剪切及张拉破坏理论 FV=KAP2f⋅P 约5.6 km秦岭隧道 完整性较好的混合花岗岩 Frenzel等[10] Cerchar磨蚀性试验(CAI) Hf=π D24⋅n⋅P1000⋅2SD⋅1000 超过127 km隧道 微风化花岗岩 Hassanpour等[11] 岩石硬度试验(VHNR) Hf=−2.669VHNR−7.891UCS+3430.955 约30 km长Karaj输水隧洞 弱风化火山岩 李刚等[12] CSM模型 Ft=TRϕPr1 + ψ, Pr=C⋅(Sσ2cσtφ√RT)1/3 约18.5 km秦岭隧道 完整较好的玄武岩、石灰岩、花岗岩 杨延栋等[13] Rabinowicz微切削原理 ω=0.16KsS13RiσcD0T16h16σs 约2 km狮子洋隧道和531 m广州地铁隧道 微风化混合花岗岩 注：Fv为滚刀法向垂直力（N），Hf为滚刀基本寿命（m3/cutter），M为滚刀径向磨损量（mm），Ft为滚刀法向和切向合力（N）。 
下载: 导出CSV
表 2 复合式土压平衡盾构机技术参数
Table 2 Technical parameters of composite EPB shield machine
参数 整机功率/kW 刀盘转速/(r·min-1) 扭矩/(kN·m) 推力/kN 推进速度/(mm·min-1) 刀盘开口率/% 滚刀数量/把 计算值 1668.05 1.8 2300 10000 15 35 41 参数 中心滚刀数量/把 正面滚刀数量/把 边滚刀数量/把 滚刀直径/mm 刀刃宽度/mm 刀刃角/(°) 刀圈硬度/HRC 计算值 6 23 12 457 19 20 60
下载: 导出CSV
表 3 微风化花岗岩力学性质及计算参数
Table 3 Mechanical properties and calculation parameters of slightly weathered granulated granite
参数 密度/(kg·m-3) 抗压强度/MPa 抗拉强度/MPa 黏聚力/MPa 内摩擦角/(°) 弹性模量/GPa 泊松比 完整性系Kv 滚压系Kn 计算值 2700 90 6.89 20.8 42.5 26.7 0.22 0.55 0.7
下载: 导出CSV
-
[1] KARAMI M, ZARE S, ROSTAMI J. Study of common wear prediction models for hard rock TBM disc cutters and comparison with field observation in Kerman water conveyance tunnel[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(2): 1467–1476. doi: 10.1007/s10064-020-01987-5
[2] TUMAC D, BALCI C. Investigations into the cutting characteristics of CCS type disc cutters and the comparison between experimental, theoretical and empirical force estimations[J]. Tunnelling and Underground Space Technology, 2015, 45: 84–98. doi: 10.1016/j.tust.2014.09.009
[3] 张照煌. 全断面岩石掘进机平面刀盘上盘形滚刀磨损研究[J]. 现代隧道技术, 2007, 44(6): 32–36. doi: 10.3969/j.issn.1009-6582.2007.06.007 ZHANG Zhao-huang. Study on the abrasion of disc cutters on full face rock tunnel boring machine[J]. Modern Tunnelling Technology, 2007, 44(6): 32–36. (in Chinese) doi: 10.3969/j.issn.1009-6582.2007.06.007
[4] YANG J H, ZHANG X P, JI P Q, et al. Analysis of disc cutter damage and consumption of TBM1 section on water conveyance tunnel at Lanzhou water source construction engineering[J]. Tunnelling and Underground Space Technology, 2019, 85: 67–75. doi: 10.1016/j.tust.2018.11.040
[5] XUE Y D, ZHAO F, ZHAO H X, et al. A new method for selecting hard rock TBM tunnelling parameters using optimum energy: a case study[J]. Tunnelling and Underground Space Technology, 2018, 78: 64–75. doi: 10.1016/j.tust.2018.03.030
[6] ROSTAMI J. Development of A Force Estimation Model for Rock Fragmentation with Disc Cutters Through Theoretical Modeling and Physical Measurement of Crushed Zone Pressure[D]. Golden: Colorado School of Mines, 1997.
[7] BRULAND A. Hard Rock Tunnel Boring[D]. Trondheim: Norwegian University of Science and Technology, 1998.
[8] 魏南珍, 沙明元. 秦岭隧道全断面掘进机刀具磨损规律分析[J]. 石家庄铁道学院学报, 1999, 12(2): 86–89. https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT902.022.htm WEI Nan-zhen, SHA Ming-yuan. The analysis of TBM cutter wear characteristic in the construction of Qinling tunnel[J]. Journal of Shijiazhuang Railway Institute, 1999, 12(2): 86–89. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT902.022.htm
[9] 张照煌, 纪昌明. 全断面岩石掘进机盘形滚刀刃破岩点弧长的解析解及应用研究[J]. 应用基础与工程科学学报, 2009, 17(2): 265–273. doi: 10.3969/j.issn.1005-0930.2009.02.012 ZHANG Zhao-huang, JI Chang-ming. Analytic solution and it's usage of arc length of rock breakage point of disc edge on full face rock tunnel boring machine[J]. Journal of Basic Science and Engineering, 2009, 17(2): 265–273. (in Chinese) doi: 10.3969/j.issn.1005-0930.2009.02.012
[10] FRENZEL C. Disc cutter wear phenomenology and their implications on disc cutter consumption for TBM[C]// 45th US Rock Mechanics/Geomechanics Symposium, 2011, San Francisco.
[11] HASSANPOUR J, ROSTAMI J, AZALI S T, et al. Introduction of an empirical TBM cutter wear prediction model for pyroclastic and mafic igneous rocks; a case history of Karaj water conveyance tunnel, Iran[J]. Tunnelling and Underground Space Technology, 2014, 43: 222–231. doi: 10.1016/j.tust.2014.05.007
[12] 李刚, 朱立达, 杨建宇, 等. 基于CSM模型的硬岩TBM滚刀磨损预测方法[J]. 中国机械工程, 2014, 25(1): 32–35. doi: 10.3969/j.issn.1004-132X.2014.01.007 LI Gang, ZHU Li-da, YANG Jian-yu, et al. A method to predict disc cutter wear extent for hard rock TBMs based on CSM model[J]. China Mechanical Engineering, 2014, 25(1): 32–35. (in Chinese) doi: 10.3969/j.issn.1004-132X.2014.01.007
[13] 杨延栋, 陈馈, 李凤远, 等. 盘形滚刀磨损预测模型[J]. 煤炭学报, 2015, 40(6): 1290–1296. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201506010.htm YANG Yan-dong, CHEN Kui, LI Feng-yuan, et al. Wear prediction model of disc cutter[J]. Journal of China Coal Society, 2015, 40(6): 1290–1296. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201506010.htm
[14] 吴俊, 袁大军, 李兴高, 等. 盾构刀具磨损机理及预测分析[J]. 中国公路学报, 2017, 30(8): 109–116, 142. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201708012.htm WU Jun, YUAN Da-jun, LI Xing-gao, et al. Analysis on wear mechanism and prediction of shield cutter[J]. China Journal of Highway and Transport, 2017, 30(8): 109–116, 142. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201708012.htm
[15] SU W L, LI X G, JIN D L, et al. Analysis and prediction of TBM disc cutter wear when tunneling in hard rock strata: a case study of a metro tunnel excavation in Shenzhen, China[J]. Wear, 2020, 446/447: 203190. doi: 10.1016/j.wear.2020.203190
[16] 龚秋明, 何冠文, 赵晓豹, 等. 掘进机刀盘滚刀间距对北山花岗岩破岩效率的影响实验研究[J]. 岩土工程学报, 2015, 37(1): 54–60. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16037.shtml GONG Qiu-ming, HE Guan-wen, ZHAO Xiao-bao, et al. Influence of different cutter spacings on rock fragmentation efficiency of Beishan granite by TBM[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 54–60. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16037.shtml
[17] 余静. 岩石机械破碎规律和破岩机理模型[J]. 煤炭学报, 1982, 7(3): 10–18. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB198203001.htm YU Jing. Rules of rock fragmentation with mechanical methods and model of rock failure mechanism[J]. Journl of China Coal Society, 1982, 7(3): 10–18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB198203001.htm
[18] 孙伟, 张旭, 赵奎山. 基于密实核理论的单滚刀多阶段受力预测模型[J]. 机械设计与制造, 2015(6): 9–12. https://www.cnki.com.cn/Article/CJFDTOTAL-JSYZ201506004.htm SUN Wei, ZHANG Xu, ZHAO Kui-shan. Multi-stage force prediction model of single disc cutter based on the dense nuclear theory[J]. Machinery Design & Manufacture, 2015(6): 9–12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSYZ201506004.htm
[19] HUO J Z, WANG W Z, SUN W, et al. The multi-stage rock fragmentation load prediction model of tunnel boring machine cutter group based on dense core theory[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(1/2/3/4): 277–289.
[20] 张桂菊, 谭青, 劳同炳. TBM盘形滚刀切削力学模型分析[J]. 中南大学学报(自然科学版), 2020, 51(10): 2792–2799. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202010011.htm ZHANG Gui-ju, TAN Qing, LAO Tong-bing. Analysis of rock breaking mechanics model for TBM disc cutter[J]. Journal of Central South University (Science and Technology), 2020, 51(10): 2792–2799. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202010011.htm
[21] 赵海鸣, 舒标, 夏毅敏, 等. 基于磨料磨损的TBM滚刀磨损预测研究[J]. 铁道科学与工程学报, 2014, 11(4): 152–158. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201404027.htm ZHAO Hai-ming, SHU Biao, XIA Yi-min, et al. Study of wear prediction for TBM cutter based on abrasive wear model[J]. Journal of Railway Science and Engineering, 2014, 11(4): 152–158. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201404027.htm
[22] RABINOWICZ, E. Friction and Wear of Materials[M]. NewYork: John Wiley & Sons, 1995.
[23] RABINOWICZ E, DUNN L A, RUSSELL P G. A study of abrasive wear under three-body conditions[J]. Wear, 1961, 4(5): 345–355.
[24] 龚秋明. 掘进机隧道掘进概论[M]. 北京: 科学出版社, 2014. GONG Qiu-ming. Introduction to Tunneling with TBMs[M]. Beijing: Science Press, 2014. (in chinese)
[25] 荆留杰, 张娜, 杨晨, 等. 基于最小破碎比能TBM滚刀间距设计方法研究[J]. 铁道学报, 2018, 40(12): 123-129. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201812019.htm JING Liu-jie, ZHANG Na, YANG Chen, et al. A design method research on TBM face cutter spacing layout based on mnimum specific energy[J]. Journal of the China Railway Society, 2018, 40(12): 123–129. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201812019.htm
[26] 徐小荷, 余静. 岩石破碎学[M]. 北京: 煤炭工业出版社, 1984. XU Xiao-he, YU Jing. Rock Breakage Thoery[M]. Beijing: China Coal Industry Publishing House, 1984. (in Chinese)
[27] ROSTAMI J. Study of pressure distribution within the crushed zone in the contact area between rock and disc cutters[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 57: 172–186.
-
期刊类型引用(21)
1. Haodi WANG，Chengjin QIN，Honggan YU，Zhinan ZHANG，Guoqiang HUANG，Zhengyang LIU，Chengliang LIU. A real-time multi-head mixed attention mechanism-based prediction method for tunnel boring machine disc cutter wear. Science China(Technological Sciences). 2025(01): 290-311 . 
必应学术
2. 刘送永，崔松，顾聪聪. 高压泡沫涨裂破岩特性试验研究. 岩土工程学报. 2025(01): 125-134 . 本站查看
3. 张鹏. 基于XGBoost的岩溶地层盾构滚刀磨损预测研究. 建筑机械化. 2025(01): 26-30 . 百度学术
4. 刘少强，许建述，杨修，唐启胜，谢兴飞，龚秋明，周小雄. TBM滚刀尖磨刃口现象及磨损演化特征. 现代隧道技术. 2025(01): 20-27+37 . 百度学术
5. 方应冉，李兴高，刘泓志，杨益，郭易东. 滚刀滑移状态下的受力与磨损仿真分析. 哈尔滨工业大学学报. 2024(05): 93-102 . 百度学术
6. 张魁，陈振宇，杨长，郑学军，张旭辉. 基于小孔应力集中的激光预钻孔条件下TBM滚刀侵岩模型建模与试验验证. 岩土工程学报. 2024(06): 1279-1288 . 本站查看
7. 郁歆鸿，高金铭，王旭. 隧道掘进机滚刀对岩石破碎的影响研究. 技术与市场. 2024(06): 101-103 . 百度学术
8. 李潮，鲁义强，陈召，易海洋，王明耀. 矿用硬岩巷道机械化掘进破岩形式研究现状及展望. 煤炭科学技术. 2024(S1): 259-268 . 百度学术
9. 杨小聪，黄丹，岳小磊，王想. 非煤矿山机械连续采矿技术研究进展与发展趋势. 有色金属(矿山部分). 2024(06): 1-24 . 百度学术
10. 刘杰，邓立营，倪志华，赵向波，杜立杰，杨刚. TBM滚刀磨损量及其使用寿命预测方法. 机械设计. 2024(10): 59-66 . 百度学术
11. 覃子秀，关启钰，张云龙，严远方，刘宗辉. 超前钻探钻进参数相互影响规律数值模拟研究. 公路工程. 2024(06): 72-78 . 百度学术
12. 杨志勇，邵小康，王鹤然，江玉生，张治港，刘招伟，李清宪. 北京漂石地层土压平衡盾构滚刀受力及磨损规律研究. 土木工程学报. 2024(S1): 1-8 . 百度学术
13. 方应冉，王希浩，曹英贵，蒋华，刘泓志，张禄，李兴高. 大直径泥水盾构常压刀盘滚刀磨损分析：以胶州湾第二海底隧道为例. 土木工程学报. 2024(S2): 167-172 . 百度学术
14. 汪海波，朱庆海，杨永庆，卢文东，罗柯柯. 中风化泥、砂岩复合地层盾构滚刀磨损机理及预测分析. 工具技术. 2023(03): 92-96 . 百度学术
15. 俞建铂，仲伟，陈乔松，陈键，黄鸿颖. 基于深度置信网络的盘形滚刀磨损预测研究. 矿山机械. 2023(05): 1-7 . 百度学术
16. 王猛，齐吉琳，皮进，沈强，曹瑞琅. 基于矿物加权硬度确定岩石磨蚀性的试验研究. 水利与建筑工程学报. 2023(03): 99-104 . 百度学术
17. 刘春生，党振乾，刘延婷，刘若涵，徐鹏，王磊，马化凯. 碟盘刀具截割煤岩温度及磨损行为研究. 煤炭学报. 2023(09): 3589-3603 . 百度学术
18. 于忠婷，任亚飞，张理蒙，范文超，张兵. 基于优劣解距离法和权重分析的滚刀综合评价. 机械工程师. 2023(10): 61-64+67 . 百度学术
19. 单义为，江玉生，邵小康，叶守杰，李琛，方显轮，王振勇. 硬岩地层盾构正面滚刀磨损规律与预测模型. 铁道标准设计. 2023(12): 136-142 . 百度学术
20. 孙振中. 砂卵石地层对盾构滚刀耐磨性影响试验研究. 建筑机械化. 2022(01): 47-50 . 百度学术
21. 高伟. TBM掘进机关键部件分析及维修技术优化. 机械管理开发. 2022(07): 349-351 . 百度学术
其他类型引用(14)
计量
- 文章访问数: 372
- HTML全文浏览量: 41
- PDF下载量: 128
- 被引次数: 35
