One-dimensional transport of transient diffusion-advection of organic contaminant through composite liners
-
摘要: 采用GMB(土工膜)/GCL(膨润土防水毯)/SL(土质垫层)复合衬垫全瞬态扩散–对流运移解析模型,考察了对流区域对污染物运移计算结果的影响;探讨了用渗滤液水头高度替代衬垫水头差的简化计算的可行性;探究了土工膜类型对复合衬垫防污阻隔性能的影响;分析了对流、扩散、吸附作用对渗沥液中典型有机污染物运移规律的影响。研究结果表明:①渗沥液水头为10,5,3,0.3 m的情况下,采用全局对流模型相比局部对流模型的击穿时间相应分别高出了233%,151%,111%,24%;②采用渗沥液水头替代水头差的简化计算结果是可行的;③采用f-HDPE土工膜的复合衬垫,其击穿时间比采用PVC,LLDPE,HDPE的分别提高了36%,33%,22%;④渗沥液水头为10,5,1 m时,忽略对流作用会使击穿时间分别被高估68%,34%,6%;⑤孔洞频数由2.5增大到50,30,10,5个/(103 m2),击穿时间分别缩短了54%,41%,16%,6%;⑥SL有效扩散系数降低90%,衬垫击穿时间提高了2~6倍;SL吸附系数从1 mL/g提升到5,15,30,50 mL/g,击穿时间分别提升了311%,1086%,2249%,3798%。以上对复合衬垫防污阻隔机理的研究结果,可为实践中衬垫的使用和改进提供一定的参考和建议。Abstract: Using the fully transient diffusion-advection transport model for transport of organic contaminant in GMB/GCL/SL composite liner, a series of parameter sensitivity studies are conducted to analyze the influences of several important parameters on the barrier performance of the composite liner. The results show that: (1) When the leachate head is 10, 5, 3 and 0.3 m, the breakthrough time obtained by the full advection model is higher by 233%, 151%, 111% and 24% than that obtained by the local advection model, respectively. (2) It is appropriate to use hw as an alternative for hd for simplification. (3) The breakthrough time of the composite liner with f-HDPE geomembrane is 36%, 33% and 22% higher than that with PVC, LLDPE and HDPE, respectively. (4) When the leachate head is 10, 5 and 1 m, the breakthrough time will be overestimated due to ignoring the effects of advection by 68%, 34% and 6%, respectively. (5) When the frequency of holes increases from 2.5 to 50, 30, 10 and 5 ha-1, the breakthrough time decreases by 54%, 41%, 16% and 6%, respectively. (6) The effective diffusion coefficient of SL decreases by 90%, and the breakthrough time of the liner increases by 2 ~ 6 times. The adsorption coefficient of SL increases from 1 mL/g to 5, 15, 30 and 50 mL/g, and the breakthrough time increases by 311%, 1086%, 2249% and 3798%, respectively. The above research results may provide some reference and suggestions for the use and improvement of the liner in practice.
-
Keywords:
- landfill /
- composite liner /
- molecular diffusion /
- advection /
- adsorption /
- transport law /
- geomembrane
-
0. 引言
复合衬垫通常由土工膜(GMB)、膨润土防水毯(GCL)以及土质垫层(SL)等组成,用来阻隔填埋场渗沥液中污染物的外泄,以防对周边的自然环境造成污染[1-8]。有机污染物是填埋场渗沥液中有害物质的重要组成,在较低浓度就可能有很强的毒性[9-11]。完整土工膜是无机污染物的优异阻隔材料,但研究表明一些可挥发有机物(VOCs)可轻易穿透土工膜材料[10-19]。此外,土工膜由于施工等原因会不可避免地存在一定的孔洞缺陷,从而形成渗沥液的泄露。这对土工膜作为渗沥液中有机污染物的有效阻隔提出了挑战。因此,研究有机污染物穿过复合衬垫的运移规律,对于揭示复合衬垫防污阻隔性能具有重要意义。
尽管不少学者提出了溶质穿过层状介质的扩散–对流解析模型,但衬垫中污染物的全瞬态扩散–对流运移解析模型很长一段时间被局限于单层或双层模型[7, 20-24]。部分学者提出了一些半稳态–半瞬态半解析模型尝试对三层结构中的运移进行模拟[25]。近来提出了三层结构的瞬态解答方法[8, 26-28]。然而,对于三层衬垫结构中污染物全瞬态运移规律的研究还未系统展开。
本文基于三层全瞬态解析模型,①考察模型考虑的对流区域对污染物在复合衬垫中运移计算结果的影响;探讨以往研究模型将渗沥液水头高度假设为衬垫水头差的合理性;探究了不同类型土工膜对GMB/ GCL/SL复合衬垫防污阻隔性能的影响;②通过对衬垫各层材料特性及相关运移参数(例如各层扩散系数、分布系数或分配系数、结构厚度等),以及服役环境等因素(例如渗沥液水头高度、褶皱长度等)的参数敏感性分析,揭示了有机污染物在GMB/GCL/SL复合衬垫中分子扩散–对流–线性吸附运移规律。
1. 三层复合衬垫瞬态解析运移模型
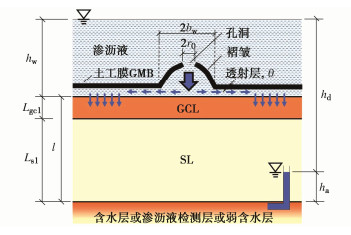
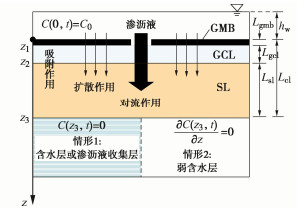
如图 1所示,复合衬垫系统由GMB,GCL和SL共3个独立水平层组成。采用分离变量法和传递矩阵法,对于污染物在GMB/GCL/SL三层复合衬垫中的运移问题,Feng等[8]将以往常用的准稳态模型提升到了全瞬态模型,并对该模型进行了详细有效的验证。对流作用和分子扩散作用在三层中均有发生,而吸附作用仅在GCL和SL层中发生。Lgmb,Lgcl,Lsl分别代表GMB,GCL和SL的厚度;Lcl是复合衬垫的厚度;hw是复合衬垫表面以上渗沥液水头的高度。模型采用了以下假设:①渗沥液中的污染物浓度恒定在C0[29];②GCL和SL均饱和且均质[30-31];③污染物符合沿z轴的一维运移过程[24];④忽略有机污染物的降解作用[24];⑤GCL和SL中污染物满足线性平衡吸附[32]。
考虑孔洞发生在褶皱上造成的渗沥液渗漏情况,有机污染物穿过GMB层瞬态的扩散–对流控制方程为[8]
∂Cgmb(z,t)∂t=Dgmb∂2Cgmb(z,t)∂z2−vaKg∂Cgmb(z,t)∂z, (1) 式中,C gmb(z, t)为均一化土工膜内t时刻在空间z位置处污染物的质量浓度,Dgmb为污染物在完整土工膜中的分子扩散系数,va为通过孔洞发生对流渗漏的达西流速,Kg为入渗界面处渗沥液和GMB间的污染物浓度分配系数。
渗沥液中污染物在GMB的入渗界面发生浓度重分配过程,假定该过程为瞬时完成,可描述为[33-34]
Cgmb(0,t)=C0Kg。 (2) 污染物穿过GCL的扩散–对流–线性吸附瞬态运移控制方程为
∂Cgcl(z,t)∂t=DgclRd, gcl∂2Cgcl(z,t)∂z2−vgclRd, gcl∂Cgcl(z,t)∂z, (3) 式中,Cgcl(z, t)为在时间t时,GCL在z位置的孔隙水中污染物的质量浓度,Dgcl为GCL的有效扩散系数,vgcl为GCL中的渗流速度,Rd, gcl为GCL的阻滞因子,
Rd, gcl=1+ρd, gclKd, gclngcl, (4) 其中,ρd, gcl为GCL的干密度,ngcl为GCL的孔隙率,Kd,gcl为GCL的分布系数,反映了GCL的吸附能力。
GMB和GCL间的连续性条件可表示为
Cgmb(Lgmb,t)K′g=Cgcl(Lgmb,t), (5) Dgmb∂Cgmb(Lgmb,t)∂z=ngclDgcl∂Cgcl(Lgmb,t)∂z, (6) 其中,K′g为污染物在GMB和GCL间的浓度分配系数,与Kg相等[18]。
污染物通过SL运移的控制方程为[26]
∂Csl(z,t)∂t=DslRd, sl∂2Csl(z,t)∂z2−vslRd, sl∂Csl(z,t)∂z, (7) 其各参数含义与GCL层(式(3))对应参数的含义类似。
GCL和SL的连续性条件可以表示为
Cgcl(Lgmb+Lgcl,t)=Csl(Lgmb+Lgcl,t), (8) ngclDgcl∂Cgcl(Lgmb+Lgcl,t)∂z=nslDsl∂Csl(Lgmb+Lgcl,t)∂z。 (9) 复合衬垫下方可能存在的底部边界条件有
Csl(Lcl,t)=0 (Dirichlet边界), (10) ∂Csl(Lcl,t)∂z=0 (Neumann边界)。 (11) 这些底部边界条件能够合理地模拟污染物通过复合衬垫底部的运移情况[35]。式(10)可表示渗漏检测层或地下水收集导排层,该层可瞬间移除系统底部所有污染物。式(11)代表了不可渗透的基础层[29]。
衬垫中污染物背景浓度为零,即初始条件为
[Cgmb(z,0)Cgcl(z,0)Csl(z,0)]=0。 (12) 参考文献[26],通过归一化方法可将上述模型转化为归一化模型,结合分离变量法和传递矩阵法,可得到模型的纯解析解答为
Ci(z,t)=ui(z)C0+wi(z,t) (i=1,2,3), (13) 式中,i为层号,1,2,3代表GMB,GCL和SL层的参数,ui(z),wi(z, t)为稳态子问题和瞬态子问题的解答。详细求解过程参见文献[26]。
图 2是通过土工膜褶皱上的孔洞渗沥液发生渗漏的示意图。对于这种孔洞在褶皱上的情况,其复合衬垫的体积渗漏量简化计算公式为[36]
QV, h=2hdLwl[kbw+√klθ] , (14) 式中,Lw为联通褶皱的长度,hd为渗沥液水头差,l为GCL和土质衬垫厚度之和,k为土工膜下卧各层的调和平均渗透系数,θ为土工膜与其紧密接触的下卧层之间的界面透射系数,又称导水率。为简化计算过程,通常将渗沥液水土差简化为土工膜上渗沥液水头高度,本文也采用了该简化方法。
对于调和平均渗透系数的计算公式为
k=Lgcl+LslLgcl/kgcl+Lsl/ksl。 (15) 则对于一个孔洞频率为mh的复合衬垫,以孔洞缺陷方式通过该复合衬垫的达西流速为[37]
va=mhQV, hA , (16) 式中,A为考察区域面积。
根据质量守恒定律,各层间的渗流速度vs与达西流速va有如下关系:
va=nvs。 (17) 从而可得到各层的渗流速度。尽管文献[26]提出了该模型,但其主要研究内容主要关注于方法本身的特性,而对于三层衬垫结构中污染物全瞬态运移规律还未有系统性研究。
本文将依托GMB/GCL/SL复合衬垫中污染物瞬态运移模型,系统研究对流作用、扩散和吸附作用对污染物在复合衬垫中运移的影响。选取甲苯作为填埋场渗沥液中的典型有机污染物[9, 25, 29, 38-40],其中土质垫层SL定为土壤保护层(AL),若未特别说明,本文后续计算模型对象均指GMB/GCL/SL复合衬垫,所需计算参数参见表 1。渗沥液中甲苯浓度假设稳定在5 mg/L。饮用水中甲苯最大允许浓度为0.7 mg/L[40-41],当衬垫底部孔隙水中甲苯浓度达到该阈值则认为衬垫被击穿。从开始发生运移到衬垫被击穿所经历的时间被定义为击穿时间tbr。土工膜上的单位公顷孔洞出现的频数mh被设定为2.5个。GMB和GCL之间的界面透射率即导水率θ取为2×10-10 m2/s[25]。褶皱半宽bw和关联贯通长度Lw取为0.1,500 m[25, 42-43]。GMB/GCL/SL复合衬垫下卧层选为常见的弱含水层,适用Neumann边界。
表 1 GMB/GCL/SL复合衬垫材料特性和服役环境参数Table 1. Parameters fo GMB/GCL/SL composite liner system参数 GMB GCL SL 厚度L/mm 0.0015[8] 0.01[8] 0.30[44] 孔隙度n — 0.70[8] 0.40[45] 干密度ρd/(g·cm-3) — 0.79[8] 1.62[8, 45] 扩散系数D/(10-10 m2·s-1) 0.003[8] 3.0[8] 8.0[8] 分配系数Kg 100[8] — — 分布系数Kd/(mL·g-1) — 8.7[46] 1.60[47] 渗透系数k/(10-9m·s-1) — 0.01[44] 100[8] 渗沥液水头高度hw/m 1 土工膜上孔洞分布密度mh 2.5[8] 褶皱长度Lw/m 500[8] 界面穿透系数θ/(10-10 m2·s-1) 2[8] 甲苯最大允许浓度Ca/(mg·L-1) 0.7[8] 渗沥液中甲苯浓度C0/(mg·L-1) 5[8] 衬垫中甲苯背景浓度Cini/(mg·L-1) 0[8] 2. 对流范围、水头差假设和土工膜类型对运移计算结果的影响
由于饮食习惯或受经济水平限制导致填埋场结构存在缺陷等原因,中国部分地区以及众多发展中国家的垃圾填埋场中的渗沥液的水头长期处于较高水平,这意味着其底部衬垫系统长期受到高渗沥液水头的作用。用于减弱乃至阻隔衬垫中对流作用的土工膜,由于施工、结构特点乃至老化等作用会存在一定的孔洞缺陷。高水头作用下,经过这些缺陷发生的对流渗漏对复合衬垫长期的防污屏障性能的影响值得设计和施工从业人员的注意。
2.1 对流范围
一般采用式(14)计算复合衬垫单孔体积渗漏量,采用式(16)计算衬垫的达西流速。该模型假设通过孔洞渗漏的液体均匀地对流通过下层衬垫的整个区域。为便于区分,本文将该常用模型称为全局达西对流模型。若通过土工膜孔洞发生的渗漏继续向GCL以及SL层发生对流的过程在横向扩展很小,极端情况假设为仅在孔洞覆盖的范围内发生对流,则该有限范围内的达西流速为
va=kzhd/l, (18) 式中,kz为z方向的渗透系数,在GMB/GCL/SL系统中可认为是土工膜下卧层的调和渗透系数。这种假设对流仅在孔洞局部发生的模型,为便于区分,本文称其为局部达西对流模型。
本节首先考察全局达西流速模型和局部达西流速模型对计算结果的影响;其次考察采用渗沥液水头hw替代渗沥液水头差hd的简化计算过程的适用性。为此选取了4个渗沥液水头高度(hw为0.3,3,5,10 m)。
假定弱含水层顶面水头高度为零,由几何关系得到渗沥液水头差矩阵为[0.61 3.31 5.31 10.31] m。由式(15)计算得到调和平均渗透系数为0.31×10-9 m/s。对于全局达西对流模型,采用式(16)计算得到达西流速矩阵为[0.0833 0.452 0.725 1.41]×10-9 m/s;对于局部达西对流模型,采用式(18)计算得到达西流速矩阵为[0.61 3.31 5.31 10.31]×10-9 m/s。
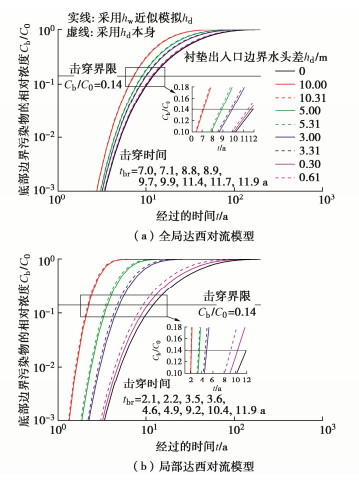
采用全局和局部达西对流模型计算所得不同水头差作用下的衬垫击穿曲线分别如图 3(a),(b)中虚线所示。全局计算模型下10.31,5.31,3.31,0.61 m水头差对应的衬垫击穿时间分别为7.0,8.8,9.7,11.4 a(图 3(a)虚线),而采用局部达西对流模型则为2.1,3.5,4.6,9.2 a(图 3(b)虚线)。全局对流模型相比局部对流模型的击穿时间相应分别高出233%,151%,111%,24%。
局部对流模型相比全局对流模型得到的击穿时间更小,是击穿时间的一个下限值,采用局部对流模型是一个更严格保守的策略。可根据实际工程对环境安全水平的要求判断是否采用该更保守的模型。例如填埋场下有下穿隧道的情况。
2.2 水头差假设
为计算简便,已有研究[8, 21-22, 26, 46, 48]通常假设穿过衬垫的水头损失hd等于渗沥液水头hw(即假设衬垫出口处的压力水头和土工膜下卧层厚度相等),本节将对该水头差简化假设的可行性进行了检验。
采纳该简化假设的衬垫上下水头差hd为0.3,3,5,10 m,不采纳该简化假设的最大水头差则为hd为0.61,3.31,5.31,10.31 m。采用该假设,则全局达西对流模型计算所得达西流速为[0.041 0.41 0.683 1.37]×10-9 m/s,局部达西对流模型所得的达西流速为[0.3 3 5 10]×10-9 m/s,计算结果分别如图 3(a),(b)中的实线所示。结果表明,除低水头情况的局部达西对流情况外,实线和相应的虚线十分贴近,表明用水头hw替代hd计算击穿曲线的简化整体是可行的,尤其对于全局达西对流模型的情况。若无特别说明,本文所采用均为全局达西模型,也都采用了水头差假设。
2.3 土工膜类型
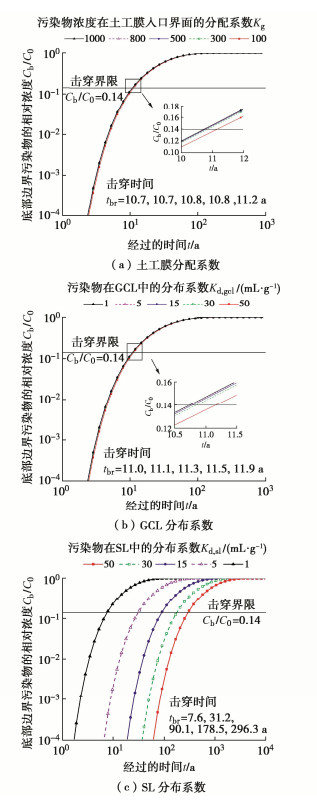
本节选用了PVC,LLDPE,HDPE,f-HDPE共4种类型的土工膜,相应运移参数见图 4。图中曲线是采用这些土工膜的GMB/GCL/SL复合衬垫击穿曲线。结果显示,采用PVC,LLDPE,HDPE,f-HDPE土工膜的复合衬垫击穿时间分别为10.7,10.9,11.9,14.5 a,可见按阻隔性能的由弱到强土工膜的排序为PVC < LLDPE < HDPE < f-HDPE。其中,表面氟化f-HDPE土工膜对复合衬垫防污阻隔性能的提升效果显著,其击穿时间相比PVC、LLDPE和HDPE的分别提升了36%,33%,22%。填埋场衬垫中采用最普遍的为HDPE土工膜,本文其他研究分析选用的也为该类型。
3. 对流作用对污染物运移的影响
本节结合Rowe等对复合衬垫土工膜发生孔洞及褶皱的试验统计结果,分析了渗沥液水头、土工膜上孔洞分布密度、连通褶皱长度、土工膜与GCL的接触条件以及各结构层的几何厚度对对流作用,乃至GMB/GCL/SL复合衬垫服役寿命的影响。
3.1 渗沥液水头
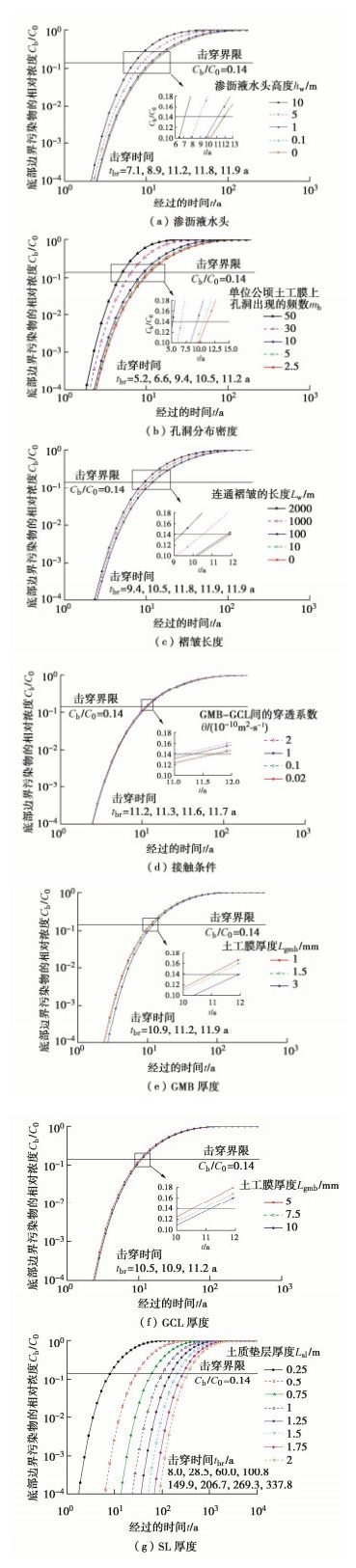
图 5(a)展示了在不同渗沥液水头高度作用下复合衬垫的击穿曲线。当水头为10,5,1,0.1,0 m时,衬垫的击穿时间分别为7.1,8.9,11.2,11.8,11.9 a。可见忽略对流作用,对于渗沥液水头为10,5,1 m的复合衬垫,其击穿时间分别会被高估68%,34%,6%。而当渗沥液水头为0.1 m时,高估率不到1%。
美国环保署(USEPA)建议填埋场渗沥液水头控制在0.3 m以内,若满足该标准,则对流对衬垫服役寿命的影响几乎可以忽略不计。反言之,当前大量高水头服役环境下的填埋场复合衬垫,对流作用对其服役寿命的削弱作用显然不可忽略。
3.2 孔洞分布密度
Giroud等[49]和Rowe等[46]的研究表明,施工过程严格遵守施工质量控制(CQC)和施工质量保证(CQA)程序,并且设置土工膜保护层以减轻土工膜所承受的张力的情况下,采用2.5~5个/(103 m2)的孔洞频率计算渗漏量进行衬垫设计是较为合理。徐亚等[50]对统计了中国80个填埋场衬垫孔洞频率情况,发现即使是具有专业施工资质并且具备专业的防渗施工经验公司施工,漏洞频率依然高达19个/(103 m2)。图 5(b)展示了不同孔洞分布频率情况下复合衬垫的击穿曲线。1000 m2土工膜上的孔洞频数为50,30,10,5,2.5的情况下复合衬垫击穿时间分别为5.2,6.6,9.4,10.5,11.2 a。孔洞频数从2.5增大到50,30,10,5,其击穿时间分别缩短了54%,41%,16%,6%。可见,控制孔洞的发生频率对于复合衬垫在长期服役过程中发挥稳定有效的防污屏障性能具有重要意义。
3.3 褶皱长度和接触条件
图 5(c)展示了连通褶皱长度5个取值(Lw为2000,1000,100,10,0 m)情况下复合衬垫的击穿曲线,其对应的击穿时间分别为9.4,10.5,11.8,11.9,11.9 a。可见褶皱不大于100 m时,对流作用对衬垫击穿时间的影响可忽略不计。褶皱长度增大10倍,对于从10 m增大到100 m和从100 m增大到1000 m的两种情况,击穿时间分别降低了不足1%和约11%。说明褶皱长度只有达到足够大时,才可能对衬垫的击穿时间产生足够影响。当褶皱长度为2000 m时,相比于无孔洞渗漏情况,击穿时间缩短了21%。表明当连通的褶皱长度达到足够长时,即使孔洞发生频数在2.5,仍然需要考虑对流作用对复合衬垫服役寿命的影响。
图 5(d)展示了GMB-GCL界面穿透系数在4个取值水平下复合衬垫的击穿曲线。由图可见一般情况下接触条件对复合衬垫的击穿时间影响较小,当穿透系数缩小了100倍(从2×10-10降低到0.02×10-10 m2/s),击穿时间(11.2,11.7 a)也仅延长了不足5%。
3.4 结构层几何厚度
图 5(e)~(g)分别展示了GMB,GCL和SL的厚度对复合衬垫击穿时间的影响。如图 5(e)所示,GMB厚度由1 mm增大到3 mm,复合衬垫的击穿时间由10.9 a延长到11.9 a,增大了9%。可见从扩散的角度看,土工膜厚度对于延长复合衬垫的击穿时间具有一定影响。如图 5(f)所示,GCL的厚度由5 mm增大到10 mm,击穿时间仅从10.5 a增大到11.2 a,增长了不到7%。综上可见,GMB以及GCL的厚度由于可变化范围较窄,其厚度对复合衬垫击穿时间的影响较为有限。
然而,如图 5(g)所示,土质垫层的厚度对复合衬垫最终的击穿时间具有显著的影响,SL8个不同厚度取值(0.25,0.5,0.75,1,1.25,1.5,1.75,2 m),其对应的复合衬垫击穿时间分别为8.0,28.5,60.0,100.8,149.9,206.7,269.3,337.8 a。随着SL厚度逐渐增大,其每增加0.25 m,击穿时间分别会增长256%,111%,68%,49%,38%,30%,25%,可见当土质垫层厚度较小时,增加其厚度对击穿时间的提升效果十分明显,也意味着设置适当厚度的土壤缓冲层对于复合衬垫击穿时间的提升效果显著。
4. 分子扩散作用对污染物运移的影响
本节拟考察污染物在各层阻隔材料中的扩散性能对复合衬垫防污阻隔性能的影响。有机污染物在土工膜的晶体间隙,以及在GCL以及SL等多孔介质的孔隙水中会发生分子扩散。衡量分子扩散在其中运移速度的宏观物理参数,对于土工膜该参数为分子扩散系数,而对于多孔介质其为有效扩散系数。
4.1 GMB的扩散系数
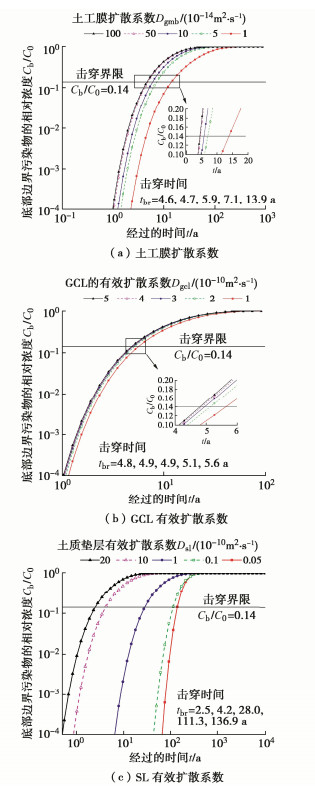
如图 6(a)所示,衬垫的击穿时间随着土工膜中的扩散系数的减小而逐渐增大,Dgmb为100×10-14,50×10-14,10×10-14,5×10-14,1×10-14 m2/s时,复合衬垫的击穿时间分别为4.6,4.7,5.9,7.1,13.9 a。可见随着土工膜扩散系数的减小,衬垫击穿时间的增加并不是一个线性的过程。例如,当土工膜扩散系数均减小一半,对于从100×10-14减半到50×10-14 m2/s的情况击穿时间(分别为4.6,4.7 a)增加了2%,而对于从10×10-14到5×10-14 m2/s的情况击穿时间(分别为5.9,7.1 a)增加了20%。当土工膜扩散系数均减小到原来的1/5,对于从50×10-14到10×10-14 m2/s的情况击穿时间(分别为4.7,5.9 a)增加了26%,而对于从5×10-14到1×10-14 m2/s的情况击穿时间(分别为7.1,13.9 a)增加了96%。
由此可见,复合衬垫的击穿时间即服役寿命对于土工膜扩散系数较大的情况敏感性较低,而土工膜扩散系数已经较小则敏感性很高。换言之,当土工膜扩散系数较大时,降低污染物在土工膜中的扩散系数对于增大复合衬垫的击穿时间(即提升衬垫的防污阻隔性能乃至服役寿命)具有一定效果,但并不显著;而当土工膜扩散系数已经足够小,继续降低土工膜的扩散系数能显著延长复合衬垫的服役寿命。因此,开发和研制低扩散系数特性的土工膜材料,对于提高复合衬垫防污屏障长期服役性能具有重要意义。
4.2 GCL有效扩散系数
图 6(b)展示的是在5个GCL有效扩散系数取值水平(Dgcl为5×10-10,4×10-10,3×10-10,2×10-10,1×10-10 m2/s)下复合衬垫的击穿曲线。如图所示,GCL有效扩散系数的减小一定程度延长了衬垫击穿时间,这与减小污染物在土工膜中的扩散系数对衬垫击穿时间影响规律类似。即,当GCL有效扩散系数在较小的情况下,继续降低污染物在GCL中的有效扩散系数能更加显著提升衬垫长期阻隔性能。
4.3 SL有效扩散系数
图 6(c)展示了5个不同土层有效扩散系数取值情况下(Dsl为20×10-10,10×10-10,1×10-10,0.1×10-10,0.05×10-10 m2/s)复合衬垫的击穿曲线。由大到小的有效扩散系数对应的击穿时间分别为2.5,4.2,28.0,111.3,136.9 a。SL层的有效扩散系数降低到原来的1/10,对于Dsl从10×10-10降低到1×10-10 m2/s,复合衬垫击穿时间(分别为4.2,28.0 a)提升了567%;而对于Dsl从1×10-10降低到0.1×10-10 m2/s,复合衬垫击穿时间(分别为28.0,111.3 a)提升了298%。显然,污染物在SL层中有效扩散系数的大小能显著地影响复合衬垫的击穿时间。
5. 吸附作用对污染物运移的影响
5.1 GMB的分配系数
渗沥液与土工膜相接触,渗沥液中的有机污染物会受到土工膜的吸附作用,因而渗沥液中有机污染物会在渗沥液和土工膜表面发生浓度重分配。这种浓度重分配过程,本质上是土工膜对渗沥液中污染物的一个吸附过程,其分配结果可简单用分配系数来描述。图 7(a)展示了土工膜分配系数5个取值(Kg为1000,800,500,300,100)情况下复合衬垫的击穿曲线。分配系数由1000降低到300,击穿时间提升极小,可忽略不计;由300降低到100,击穿时间(10.8,11.2 a)也仅提升了4%。结果表明土工膜分配系数对复合衬垫击穿时间的影响可忽略不计。
5.2 GCL的分布系数
采用了瞬时线性吸附模型描述污染物在多孔介质中的吸附过程。关键参数即分布系数Kd是吸附浓度和溶解浓度的比值。图 7(b)是GCL层中污染物分布系数在5个取值(Kd, gcl为1,5,15,30,50 mL/g)水平下复合衬垫的击穿曲线。Kd, gcl从1 mL/g增大到50 mL/g,击穿时间(11.0,11.9 a)也仅增加了8%,可见在扩散-对流-吸附耦合作用下,GCL中的吸附作用对GMB/GCL/SL复合衬垫服役寿命的影响同样较为有限。
5.3 SL的分布系数
图 7(c)是SL层对污染物分布系数在5个取值(Kd, sl为1,5,15,30,50 mL/g)情况下复合衬垫的击穿曲线。
如图 7所示,土层对其中污染物的吸附作用显然对复合衬垫击穿时间产生了显著的影响,Kd, sl为1,5,15,30,50 mL/g时复合衬垫的击穿时间分别为7.6,31.2,90.1,178.5,296.3 a。土层吸附系数从1 mL/g提升到5,15,30,50 mL/g,复合衬垫击穿时间的提升率分别高达311%,1086%,2249%,3798%。因此,提高衬垫土层对污染物的吸附性能,对于提升衬垫长期服役性能效果显著。
需特别指出的是,本文采用瞬时线性吸附模型,该模型假设土颗粒对污染物的吸附能力是无限的,而实际情况一般会存在一个最大吸附量,因此本研究得到的结果可作为吸附能力处于理想状态下的一组结果,对于浓溶液,实际吸附效果会低于上述结果。
6. 结论
本文依托GMB/GCL/SL扩散–对流–线性吸附瞬态运移模型,对潜在影响衬垫防污阻隔性能的重要参数展开了敏感性分析;随后,对比了局部和全局对流模型,以及土工膜类型对衬垫防污阻隔性能的影响。得到8点主要结论。
(1)渗沥液水头为10,5,3,0.3 m的情况下,采用全局对流模型相比局部对流模型的击穿时间相应分别高出了233%,151%,111%,24%,采用局部对流模型相比全局对流模型计算所得的击穿时间更小,是击穿时间的一个下限值,采用局部对流模型是一个更加严格、保守的方法。
(2)为简化计算,将穿过衬垫的水头损失hd假设等于渗沥液水头hw预测污染物穿过复合衬垫的运移过程,该假设是可行的。
(3)按阻隔性能的由弱到强土工膜的排序为PVC < LLDPE < HDPE < f-HDPE。表面氟化f-HDPE土工膜能显著提升复合衬垫防污阻隔性能,采用其的GMB/GCL/SL复合衬垫的击穿时间相比采用PVC,LLDPE,HDPE的分别提升了36%,33%和22%。
(4)渗沥液水头为10,5,1 m时,忽略对流作用,复合衬垫的击穿时间分别会被高估68%,34%,6%。当渗沥液水头为0.1 m时,高估率不到1%。若渗沥液水头控制在0.3 m以内,对流对衬垫服役寿命的影响几乎可以忽略不计,而若不低于1 m,即使对于施工质量控制良好的情况,对流对衬垫击穿时间的影响也不可忽略。
(5)孔洞频数由2.5增大到50,30,10,5个/(103 m2),复合衬垫击穿时间分别缩短了54%,41%,16%,6%,可见控制孔洞的发生频次对复合衬垫防污阻隔性能具有重要意义。当褶皱长度为2000 m时,击穿时间相比无对流情况缩短了21%。表明当连通的褶皱长度足够长时,即使孔洞发生频数仅2.5,仍需考虑对流作用对复合衬垫服役寿命的影响。而当褶皱长度不大于100 m时,对流作用对于衬垫击穿时间的影响可忽略不计。此外,GMB-GCL接触条件的影响也较小。
(6)SL层有效扩散系数能显著影响复合衬垫的击穿时间,当其降低90%,复合衬垫的击穿时间可提高2~6倍。当GMB扩散系数较小时,降低GMB扩散系数对于延长复合衬垫的击穿时间效果显著。GCL有效扩散系数的变化范围有限,对提升复合衬垫击穿时间的效果较小。
(7)SL吸附作用可显著提升复合衬垫的防污阻隔性能,SL吸附系数从1 mL/g提升到5,15,30,50 mL/g,复合衬垫击穿时间分别提升了311%,1086%,2249%,3798%。而GMB吸附作用对复合衬垫击穿时间的影响几乎可忽略不计。GCL吸附作用对击穿时间有一定的影响,但效果较小。
(8)配置8个不同厚度SL(0.25,0.5,0.75,1,1.25,1.5,1.75,2 m)的GMB/GCL/SL复合衬垫,SL每增加0.25 m,其击穿时间增长率分别为256%,111%,68%,49%,38%,30%,25%。可见总体上土质垫层的厚度对复合衬垫的击穿时间具有显著的提升作用,且当土质垫层厚度较小时,增加其厚度对击穿时间的提升效率十分显著。土工膜厚度由1 mm增大到3 mm时,复合衬垫的击穿时间由10.9 a延长到11.9 a,增大了9%。GCL的厚度由5 mm增大到10 mm,击穿时间从10.5 a增大到11.2 a,增长了不到7%。土工膜以及GCL的厚度由于变化范围较为有限,其厚度对复合衬垫的击穿时间的影响较为有限。
-
表 1 GMB/GCL/SL复合衬垫材料特性和服役环境参数
Table 1 Parameters fo GMB/GCL/SL composite liner system
参数 GMB GCL SL 厚度L/mm 0.0015[8] 0.01[8] 0.30[44] 孔隙度n — 0.70[8] 0.40[45] 干密度ρd/(g·cm-3) — 0.79[8] 1.62[8, 45] 扩散系数D/(10-10 m2·s-1) 0.003[8] 3.0[8] 8.0[8] 分配系数Kg 100[8] — — 分布系数Kd/(mL·g-1) — 8.7[46] 1.60[47] 渗透系数k/(10-9m·s-1) — 0.01[44] 100[8] 渗沥液水头高度hw/m 1 土工膜上孔洞分布密度mh 2.5[8] 褶皱长度Lw/m 500[8] 界面穿透系数θ/(10-10 m2·s-1) 2[8] 甲苯最大允许浓度Ca/(mg·L-1) 0.7[8] 渗沥液中甲苯浓度C0/(mg·L-1) 5[8] 衬垫中甲苯背景浓度Cini/(mg·L-1) 0[8] -
[1] BARROSO M, TOUZE-FOLTZ N, VON MAUBEUGE K, et al. Laboratory investigation of flow rate through composite liners consisting of a geomembrane, a GCL and a soil liner[J]. Geotextiles and Geomembranes, 2006, 24(3): 139–155. doi: 10.1016/j.geotexmem.2006.01.003
[2] BOUAZZA A, BOWDERS J. Geosynthetic Clay Liners for Waste Containment Facilities[M]. Boca Raton: CRC Press, 2009.
[3] VARANK G, DEMIR A, YETILMEZSOY K, et al. Estimation of transport parameters of phenolic compounds and inorganic contaminants through composite landfill liners using one-dimensional mass transport model[J]. Waste Management, 2011, 31(11): 2263–2274. doi: 10.1016/j.wasman.2011.06.005
[4] EL-ZEIN A, MCCARROLL I, TOUZE-FOLTZ N. Three-dimensional finite-element analyses of seepage and contaminant transport through composite geosynthetics clay liners with multiple defects[J]. Geotextiles and Geomembranes, 2012, 33: 34–42. doi: 10.1016/j.geotexmem.2012.02.004
[5] PARK M G, EDIL T B, BENSON C H. Modeling volatile organic compound transport in composite liners[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2012, 138(6): 641–657. doi: 10.1061/(ASCE)GT.1943-5606.0000630
[6] HOOR A, ROWE R K. Potential for desiccation of geosynthetic clay liners used in barrier systems[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(10): 1648–1664. doi: 10.1061/(ASCE)GT.1943-5606.0000899
[7] GUAN C, XIE H J, WANG Y Z, et al. An analytical model for solute transport through a GCL-based two-layered liner considering biodegradation[J]. Science of the Total Environment, 2014, 466/467: 221–231. doi: 10.1016/j.scitotenv.2013.07.028
[8] FENG S J, PENG M Q, CHEN H X, et al. Fully transient analytical solution for degradable organic contaminant transport through GMB/GCL/AL composite liners[J]. Geotextiles and Geomembranes, 2019, 47(3): 282–294. doi: 10.1016/j.geotexmem.2019.01.017
[9] KJELDSEN P, BARLAZ M A, ROOKER A P, et al. Present and long-term composition of MSW landfill leachate: a review[J]. Critical Reviews in Environmental Science and Technology, 2002, 32(4): 297–336. doi: 10.1080/10643380290813462
[10] EDIL T B. A review of aqueous-phase VOC transport in modern landfill liners[J]. Waste Management, 2003, 23(7): 561–571. doi: 10.1016/S0956-053X(03)00101-6
[11] ISLAM M Z, ROWE R K. Effect of geomembrane ageing on the diffusion of VOCS through HDPE geomembranes[C]// The First Pan American Geosynthetics Conference & Exhibition, 2008(March): 459–467.
[12] PARK J K, NIBRAS M. Mass flux of organic chemicals through polyethylene geomembranes[J]. Water Environment Research, 1993, 65(3): 227–237. doi: 10.2175/WER.65.3.6
[13] PRASAD T V, BROWN K W, THOMAS J C. Diffusion coefficients of organics in high density polyethylene (HDPE)[J]. Waste Management & Research, 1994, 12(1): 61–71.
[14] ROWE R K, HRAPOVIC L, KOSARIC N. Diffusion of chloride and dichloromethane through an HDPE geomembrane[J]. Geosynthetics International, 1995, 2(3): 507–536. doi: 10.1680/gein.2.0021
[15] SANGAM H P, ROWE R K. Migration of dilute aqueous organic pollutants through HDPE geomembranes[J]. Geotextiles and Geomembranes, 2001, 19(6): 329–357. doi: 10.1016/S0266-1144(01)00013-9
[16] TOUZE-FOLTZ N, ROSIN-PAUMIER S, MAZÉAS L, et al. Diffusion of volatile organic compounds through an HDPE geomembrane[C]// Geo-Frontiers Congress 2011, 2011, Dallas.
[17] MCWATTERS R S, ROWE R K. Permeation of volatile organic compounds through EVOH thin film membranes and coextruded LLDPE/EVOH/LLDPE geomembranes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(2): 04014091. doi: 10.1061/(ASCE)GT.1943-5606.0001209
[18] ROWE R K, SAHELI P T, RUTTER A. Partitioning and diffusion of PBDEs through an HDPE geomembrane[J]. Waste Management (New York), 2016, 55: 191–203. doi: 10.1016/j.wasman.2016.05.006
[19] ROWE R K, JONES D D, RUTTER A. Polychlorinated biphenyl diffusion through HDPE geomembrane[J]. Geosynthetics International, 2016, 23(6): 408–421. doi: 10.1680/jgein.16.00006
[20] 谢海建, 楼章华, 陈云敏, 等. 污染物通过GCL/AL防渗层的对流-弥散解析解[J]. 科学通报, 2010, 55(21): 2148–2155. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201021014.htm XIE Hai-jian, LOU Zhang-hua, CHEN Yun-min, et al. An analytical solution to contaminant advection and dispersion through a GCL/AL liner system[J]. Chinese Science Bulletin, 2010, 55(21): 2153–2163. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB201021014.htm
[21] 谢海建, 陈云敏, 楼章华. 污染物通过有缺陷膜复合衬垫的一维运移解析解[J]. 中国科学: 技术科学, 2010, 40 (5): 486–495. doi: 10.3969/j.issn.0253-2778.2010.05.0008 XIE Hai-jian, CHEN Yun-min, LOU Zhang-hua. An analytical solution to contaminant transport through composite liners with geomembrane defects[J]. Scientia Sinica Technologica, 2010, 40(5): 486–495. (in Chinese) doi: 10.3969/j.issn.0253-2778.2010.05.0008
[22] LI Y C, CLEALL P J. Analytical solutions for advective-dispersive solute transport in double-layered finite porous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(4): 438–460. doi: 10.1002/nag.903
[23] 张文杰, 黄依艺, 张改革. 填埋场污染物在有限厚度土层中一维对流–扩散–吸附解析解[J]. 岩土工程学报, 2013, 35(7): 1197–1201. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15098.shtml ZHANG Wen-jie, HUANG Yi-yi, ZHANG Gai-ge. Analytical solution for 1D advection-diffusion-adsorption transport of landfill contaminants through a soil layer with finite thickness[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1197–1201. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15098.shtml
[24] CHEN Y M, WANG Y Z, XIE H J. Breakthrough time-based design of landfill composite liners[J]. Geotextiles and Geomembranes, 2015, 43(2): 196–206. doi: 10.1016/j.geotexmem.2015.01.005
[25] XIE H J, THOMAS H R, CHEN Y M, et al. Diffusion of organic contaminants in triple-layer composite liners: an analytical modeling approach[J]. Acta Geotechnica, 2015, 10(2): 255–262. doi: 10.1007/s11440-013-0262-3
[26] FENG S J, PENG M Q, CHEN Z L, et al. Transient analytical solution for one-dimensional transport of organic contaminants through GM/GCL/SL composite liner[J]. Science of the Total Environment, 2019, 650: 479–492. doi: 10.1016/j.scitotenv.2018.08.413
[27] PENG M Q, FENG S J, CHEN H X, et al. Analytical model for organic contaminant transport through GMB/CCL composite liner with finite thickness considering adsorption, diffusion and thermodiffusion[J]. Waste Management, 2021, 120: 448–458. doi: 10.1016/j.wasman.2020.10.004
[28] PENG M Q, FENG S J, CHEN H X, et al. An analytical solution for organic pollutant diffusion in a triple-layer composite liner considering the coupling influence of thermal diffusion[J]. Computers and Geotechnics, 2021, 137: 104283. doi: 10.1016/j.compgeo.2021.104283
[29] CHEN Y M, XIE H J, KE H, et al. An analytical solution for one-dimensional contaminant diffusion through multi-layered system and its applications[J]. Environmental Geology, 2009, 58(5): 1083–1094. doi: 10.1007/s00254-008-1587-3
[30] BENSON C H, DANIEL D E, BOUTWELL G P. Field performance of compacted clay liners[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(5): 390–403. doi: 10.1061/(ASCE)1090-0241(1999)125:5(390)
[31] STARK T D. Evaluation of a four-component composite landfill liner system[J]. Environmental Geotechnics, 2017, 4(4): 257–273. doi: 10.1680/jenge.14.00033
[32] ROWE R K. Geosynthetics and the minimization of contaminant migration through barrier systems beneath solid waste[C]//Proceedings of the 6th International Conference on Geosynthetics, 1998, Atlanta.
[33] LEO A, HANSCH C, ELKINS D. Partition coefficients and their uses[J]. Chemical Reviews, 1971, 71(6): 525–616. doi: 10.1021/cr60274a001
[34] SANGAM H P, ROWE R K. Effect of surface fluorination on diffusion through a high density polyethylene geomembrane[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(6): 694–704. doi: 10.1061/(ASCE)1090-0241(2005)131:6(694)
[35] FOOSE G J. Transit-time design for diffusion through composite liners[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(7): 590–601. doi: 10.1061/(ASCE)1090-0241(2002)128:7(590)
[36] ROWE R K, CHAPPEL M J, BRACHMAN R W I, et al. Field study of wrinkles in a geomembrane at a composite liner test site[J]. Canadian Geotechnical Journal, 2012, 49(10): 1196–1211. doi: 10.1139/t2012-083
[37] ROWE R K, BRACHMAN R W I. Assessment of equivalence of composite liners[J]. Geosynthetics International, 2004, 11(4): 273–286. doi: 10.1680/gein.2004.11.4.273
[38] FOOSE G J, BENSON C H, EDIL T B. Equivalency of composite geosynthetic clay liners as a barrier to volatile organic compounds[C]//Proceedings of Geosynthetics. 1999, Boston.
[39] FOOSE G J, BENSON C H, EDIL T B. Analytical equations for predicting concentration and mass flux from composite liners[J]. Geosynthetics International, 2001, 8(6): 551–575. doi: 10.1680/gein.8.0206
[40] XIE H J, JIANG Y S, ZHANG C H, et al. Steady-state analytical models for performance assessment of landfill composite liners[J]. Environmental Science and Pollution Research, 2015, 22(16): 12198–12214. doi: 10.1007/s11356-015-4200-9
[41] ACAR Y B, HAIDER L. Transport of low-concentration contaminants in saturated earthen barriers[J]. Journal of Geotechnical Engineering, 1990, 116(7): 1031–1052. doi: 10.1061/(ASCE)0733-9410(1990)116:7(1031)
[42] CHAPPEL M J, ROWE R K, BRACHMAN R W I, et al. A comparison of geomembrane wrinkles for nine field cases[J]. Geosynthetics International, 2012, 19(6): 453–469. doi: 10.1680/gein.12.00030
[43] ROWE R K. Short- and long-term leakage through composite liners[J]. Can Geotech J, 2012, 49(2): 141–169. doi: 10.1139/t11-092
[44] 生活垃圾卫生填埋处理技术规范: GB 50869—2013[S]. 2014. Technical Code for Municipal Solid Waste Sanitary Landfill: GB 50869—2013[S]. 2014. (in Chinese)
[45] XIE H J, LOU Z H, CHEN Y M, et al. An analytical solution to contaminant advection and dispersion through a GCL/AL liner system[J]. Chinese Science Bulletin, 2011, 56(8): 811–818. doi: 10.1007/s11434-010-4039-x
[46] ROWE R K. Long-term performance of contaminant barrier systems[J]. Géotechnique, 2005, 55(9): 631–678. doi: 10.1680/geot.2005.55.9.631
[47] LAKE C B, ROWE R K. A comparative assessment of volatile organic compound (VOC) sorption to various types of potential GCL bentonites[J]. Geotextiles and Geomembranes, 2005, 23(4): 323–347. doi: 10.1016/j.geotexmem.2005.01.001
[48] XIE H J, JIANG Y S, ZHANG C H, et al. An analytical model for volatile organic compound transport through a composite liner consisting of a geomembrane, a GCL, and a soil liner[J]. Environmental Science and Pollution Research International, 2015, 22(4): 2824–2836. doi: 10.1007/s11356-014-3565-5
[49] GIROUD J P, BONAPARTE R. Geosynthetics in liquid-containing structures[M]// Geotechnical and Geoenvironmental Engineering Handbook. Boston: Springer, 2001.
[50] 徐亚, 能昌信, 刘玉强, 等. 垃圾填埋场HDPE膜漏洞密度及其影响因素的统计分析[J]. 环境工程学报, 2015, 9(9): 4558–4564. https://www.cnki.com.cn/Article/CJFDTOTAL-HJJZ201509076.htm XU Ya, NAI Chang-xin, LIU Yu-qiang, et al. Statistical analysis on density of accidental-hole in landfill liner system[J]. Chinese Journal of Environmental Engineering, 2015, 9(9): 4558–4564. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HJJZ201509076.htm
-
期刊类型引用(5)
1. 裘智超,彭明清,徐辉,沈斯亮. 有机污染物在含缺陷土工膜复合隔离墙中一维运移解析研究. 环境科学学报. 2025(02): 226-238 .  百度学术
百度学术
2. 江文豪,冯晨,李江山. 考虑温度变化下三层复合衬垫中重金属污染物一维运移理论模型. 岩土力学. 2024(02): 417-432 .  百度学术
百度学术
3. 张春华,黄江东,邓正定,谢海建,邓通发. 热渗透作用下有机污染物在双人工复合衬层中的一维运移模型. 岩土工程学报. 2024(06): 1254-1262 .  本站查看
本站查看
4. 李天义,孙德安,傅贤雷,陈征,汪磊,杜延军. 考虑时变污染源与土工膜破损的污染物二维迁移特性. 岩土工程学报. 2024(11): 2450-2456 .  本站查看
本站查看
5. 李江山,江文豪,冯晨. 非等温分布条件下三层复合衬垫中有机污染物一维瞬态运移规律研究. 岩土力学. 2023(09): 2717-2731 .  百度学术
百度学术
其他类型引用(7)



 下载:
下载: