高级切线模量法及其在地基沉降计算中的应用

杨光华; 李卓勋; 王东英; 李志云; 姜燕

doi:10.11779/CJGE202205001

高级切线模量法及其在地基沉降计算中的应用 English Version

杨光华^{1, 2, 3,},
李卓勋¹,
王东英^{2, 3},
李志云^{2, 3},
姜燕^{2, 3}

1.
华南理工大学土木与交通学院, 广东广州 510640
2.
广东省水利水电科学研究院, 广东广州 510610
3.
广东省岩土工程技术研究中心, 广东广州 510610

基金项目:

国家自然科学基金项目 52078143

详细信息

作者简介:
杨光华(1962—)，男，广东罗定人，博士，教授级高级工程师，博士生导师，主要从事本构理论、基础工程、软土工程及基坑工程等方面的研究、设计及咨询工作。E-mail: 1084242143@qq.com

中图分类号: TU433
计量
- 文章访问数: 308
- HTML全文浏览量: 20
- PDF下载量: 262
出版历程
- 收稿日期: 2021-03-01
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-04-30

Advanced tangent modulus method and its application to calculation of foundation settlement

YANG Guang-hua^{1, 2, 3,},
LI Zhuo-xun¹,
WANG Dong-ying^{2, 3},
LI Zhi-yun^{2, 3},
JIANG Yan^{2, 3}

1.
Department of Civil Engineering, South China University of Technology, Guangzhou 510640, China
2.
Guangdong Research Institute of Water Resources and Hydropower, Guangzhou 510610, China
3.
The Geotechnical Engineering Technology Center of Guangdong Province, Guangzhou 510610, China

摘要

摘要: 切线模量法方法简单、参数少，易于工程应用，研究表明在计算常规尺寸的基础时具有较好的精度，而对于筏板这样的大尺寸基础时，当计算深度较深时，存在计算沉降偏大的问题。为此提出了考虑初始切线模量沿深度增大的高级切线模量法，通过与实际工程案例和小应变有限元数值计算方法结果比较，高级切线模量法能更符合实际，进一步发展完善了切线模量法。
- 切线模量法 /
- 地基沉降 /
- 有限元 /
- 小应变硬化土模型
Abstract: The tangent modulus method proposed by YANG Guang-hua is simple, with few parameters and easy for engineering application. The researches have shown that it has better accuracy when calculating the foundations with conventional dimensions, but for the large-sized foundations such as rafts, the calculated settlement is too large. For this reason, an advanced tangent modulus method considering the increase of the initial tangent modulus extension depth is proposed. The comparison with the actual engineering case and the calculated results by the finite element method of the small-strain hardening soil model shows that the advanced tangent modulus method can be more realistic. This further develops and improves the tangent modulus method.
- tangent modulus method /
- foundation settlement /
- finite element /
- small-strain hardening soil model

HTML全文

0. 引言

对于地基设计而言，怎样准确地计算地基沉降一直是岩土工程中的一大难题，虽然现在已发展出很多先进的计算方法, 如有限元法等，但由于土体的复杂性，土的本构模型的选择往往对计算结果有较大的影响，复杂的本构模型，如小应变硬化土（HSS）模型^[1]，需大量参数来支撑计算的精确性，简单模型如线弹性模型则很难反映出土体的非线性弹塑性的特点。因此，要如何准确地计算地基的变形与沉降还是一个非常值得研究的问题。在工程实践中，现行的地基沉降计算方法最常用的是国家规范中半理论半经验的分层总和法^[2]：

$s = {\psi _{\text{s}}}s' = {\psi _{\text{s}}}\sum\limits_{i = 1}^n {\frac{{{p_0}}}{{{E_{{\text{s}}i}}}}} ({z_i}{\bar a_i} - {z_i}{\bar a_{i - 1}}){\rm{。}}$

(1)

该方法的优点是简便，考虑了土体层状分布的特点，而分层总和法的缺点则在于没有考虑土体的非线性与原状性。该方法的修正经验系数 ${\psi _{\text{s}}}$ =0.2~1.4。对坚硬地基，修正经验系数取小值，最小为0.2，说明理论计算得出的沉降值要比实测值偏大，从而采用小于1的经验系数进行修正；而当地基比较软弱时，理论计算的值则偏小，则取修正经验系数大于1。这是因为硬土室内试验测得的变形参数比原状土的小，而软土具有较强的非线性。针对这一问题，杨光华^[3]依据原位压板载荷试验，提出了原状土沉降计算的切线模量法，其假设压板载荷试验曲线为一双曲线方程：

$p = \frac{s}{{a + bs}} {\rm{。}}$

(2)

建立了原状土的切线模量与荷载水平关系的切线模量方程：

${E_{\text{t}}} = {\left( {1 - {R_{\text{f}}}\frac{p}{{{p_{\text{u}}}}}} \right)^2}{E_{{\text{t0}}}} {\rm{。}}$

(3)

该方法计算时需要用到的参数较少，只需要土的黏聚力c、内摩擦角 $\varphi$ 以及初始切线模量E_t0共3个参数即可计算地基的非线性沉降，初始切线模量E_t0可由式（2）的a计算得到，见后面的式（5），地基极限承载力 ${p_{\text{u}}}$ 可由c和 $\varphi$ 计算得到。该法具有简便优点的同时，也具有较高的精度，许多实际案例^[4]已证明了其实用性。由于参数来自于原位试验，切线模量法既克服了室内试样扰动，又考虑了荷载水平的影响，比较符合土的变形特性，极大的推进了地基非线性沉降计算方法的发展。

在切线模量法中，影响土体切线模量E_t的主要因素为作用于地基的荷载 $p$ 、地基极限承载力 ${p_{\text{u}}}$ 以及土体的初始切线模量E_t0。当深度增大时，荷载 $p$ 由于应力扩散而减小，地基极限承载力 ${p_{\text{u}}}$ 则随深度的增加会增大，在原状土切线模量法中初始切线模量E_t0由于被视为土体本身性质决定的模量参数，它不随深度变化，取值一般为2倍的变形模量E₀^[5-6]。然而，由土的Duncan-Chang模型可知^[7]，土的初始模量是随围压的增大而增大的，则深层土的初始切线模量E_t0应该是随深度而增大的。当基础尺寸较小时，由于荷载影响深度较浅，这个规律对计算结果影响不大，但是当基础尺寸较大时，随着荷载影响深度的增大，E_t0沿深度增加可能会对计算结果造成较大的影响。为解决这一问题，本文在切线模量法的基础上挖掘出初始切线模量E_t0随深度变化的规律，提出了高级切线模量法，并将这一成果应用于实际工程中，进一步完善了原状土的切线模量法。

1. 切线模量法在不同基础尺寸下与小应变模型等数值方法结果的比较

现运用有限元分析方法，采用小应变硬化土（HSS）模型、莫尔-库仑模型以及线弹性模型对某一土体不同尺寸的压板荷载试验进行模拟，并与切线模量法算得的结果进行对比。为方便分析，本次计算中将土层设为均质土层，参考一种伦敦黏土的参数，各本构模型参数取值见表 1~3。莫尔-库仑模型与线弹性模型的模量取变形模量，具体为式（5）中计算出地表处初始切线模量E_t0的1/2。

表 1 有限元小应变硬化土模型参数取值

Table 1. Mechanical parameter of soil for small strain hardened model

土层	$\gamma$ /(kN·m^-3)	${\nu _{{\text{ur}}}}$	c/kPa	$\varphi$ /(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
伦敦黏土	18.44	0.2	2	24	0.59	100	0.5	40	6.73	8	16	9.68×10^-4

下载: 导出CSV

| 显示表格

表 2 莫尔-库仑模型参数取值

Table 2. Mechanical parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
伦敦黏土	18.44	0.3	2	24	7.3

下载: 导出CSV

| 显示表格

表 3 线弹性模型参数取值

Table 3. Mechanical parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
伦敦黏土	18.44	0.3	7.3

下载: 导出CSV

| 显示表格

1.1 小尺寸压板的对比

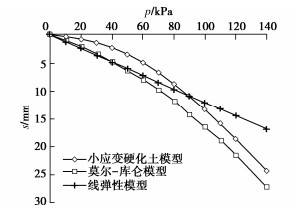
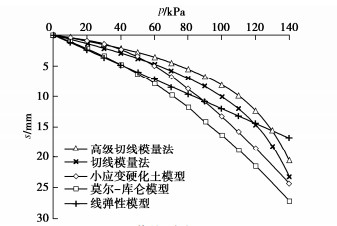
对地表位置1 m×1 m压板载荷试验进行模拟，压板上方分级加载时，将荷载设为每级10 kPa，观察上方荷载为10~120 kPa时压板底部沉降的情况，各模型计算结果如图 1。

图 1 各模型计算所得p–s曲线

Figure 1. p–s curves calculated by various models

下载: 全尺寸图片幻灯片

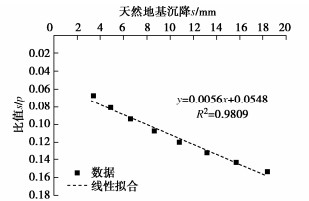
为了确定切线模量法的参数，现用图 1中小应变硬化土模型所得p–s曲线进行该土体E_t0的计算，对p–s曲线进行双曲线拟合，得到s/p–s的线性拟合结果见图 2，线性拟合方程为

$\frac{s}{p} = 0.0056s + 0.0548{, }$

(4)

图 2 s与s/p拟合曲线

Figure 2. Fitting curves of s and s/p

下载: 全尺寸图片幻灯片

相对应式（2），b=0.0056，a=0.0548，由此可求得地表处土体的初始切线模量E_t0^[3]，即

${E_{{\text{t0}}}} = \frac{{D{{(1 - \mu )}^2}\omega }}{a} = 14.61{\text{ MPa}}{\rm{。}}$

(5)

这样，结合土体的c， $\varphi$ 值即可得到切线模法的3个参数。然后采用切线模量法计算该工况的p–s曲线，计算时基础宽度b=1 m，埋深d=0 m，基础施加每级荷载增量为10 kPa，即 $\Delta p$ =10 kPa，分层厚度 $\Delta h$ =0.5 m，取压板以下每层土的中心点位置进行计算，计算深度h取10 m，可分为20层。以第一层荷载计算p=10 kPa为例说明计算过程。其中计算时选取的E_t0为由式（5）计算出的结果，取14.61 MPa。

基础中心点不同深度土体的附加应力用弹性力学的方法计算。第一级荷载下，第一层土计算深度 ${z_1} = 0.25{\text{ m}}$ ，其附加应力系数K_c= 0. 9299，则该深度处附加应力： $\Delta {\sigma _{\text{1}}} = 9.299{\text{ kPa}}$ ， ${p_{\text{u}}} =$ ${\text{169}}{\text{.9 kPa}}$ 。

该层土的切线模量为 ${E_{\text{t}}}_{\text{1}} = {\text{13}}{\text{.06 MPa}}$ 。则第一层的沉降 $\Delta {s}_{1}=0.36\text{ mm}。$

第二层土计算深度 ${z_1} = 0.75{\text{ m}}$ ，附加应力系数K_c= 0.4842，则该深度处附加应力 $\Delta {\sigma _{\text{2}}} = 4.84{\text{ kPa}}$ ， ${p_{\text{u}}} = {\text{258}}{\text{.5 kPa}}$ 。

该层土的切线模量为 ${E_{\text{t}}}_{\text{2}} = {\text{14}}{\text{.07 MPa}}$ 。则第二层的沉降为 $\Delta {s_2} = 0.17{\text{ mm}}$ 。

以此类推，可求得每一层土的沉降值，将每一层土的沉降值叠加，最终求得第一级荷载10 kPa下土体的最终沉降值： ${s_1} = 0.8{\text{ mm}}$ 。

由于有限元计算时基础为刚性基础，而切线模量法计算时为柔性基础（未考虑基础刚性），故最终计算结果也应考虑基础刚性，在计算结果的基础上乘以系数0.8作为最终结果，即 ${s'_1} = 0.64{\text{ mm}}$ 。

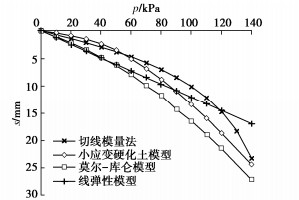
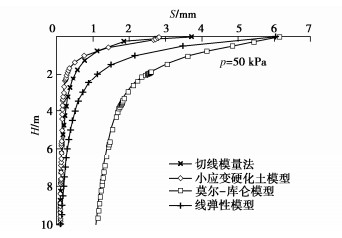
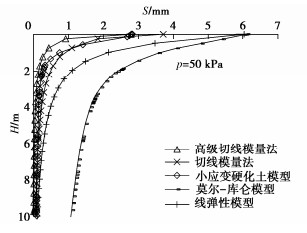
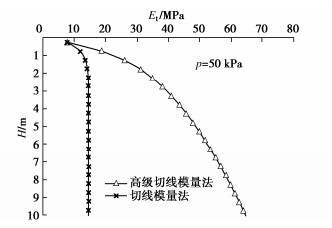
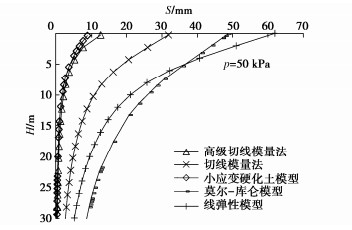
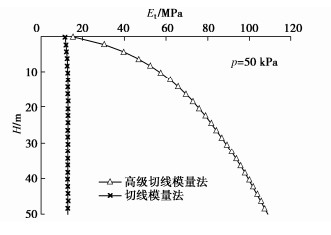
重复以上过程，可求得每级荷载下的沉降值，根据计算结果绘制p–s曲线，与有限元方法计算结果对比见图 3。绘制出当p=50 kPa时压板中心点以下土体沉降随深度变化的曲线（H–S曲线）对比图见图 4。图中结果表明：对应这个压板尺寸时，几种方法算得的最终沉降量比较接近，用切线模量法计算沉降时，荷载的影响深度也比较接近小应变硬化土模型，影响深度较小，符合实际情况，而莫尔-库仑模型以及线弹性模型计算出的影响深度较大。

图 3 各方法p–s曲线对比图(1 m×1 m)

Figure 3. Comparison of p–s curves by various methods (1 m×1 m)

下载: 全尺寸图片幻灯片

图 4 各方法H–S曲线对比图(1 m×1 m)

Figure 4. Comparison of H–S curves by various methods (1 m×1 m)

下载: 全尺寸图片幻灯片

1.2 不同基础尺寸的对比

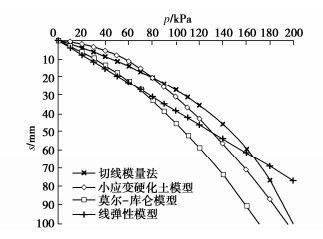
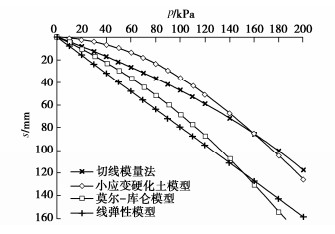
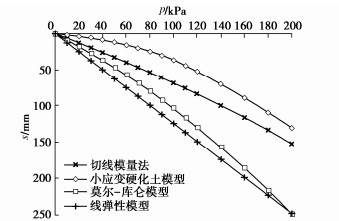
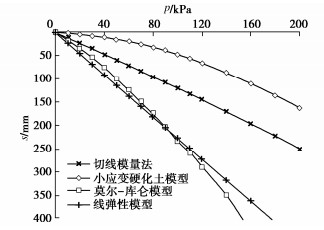
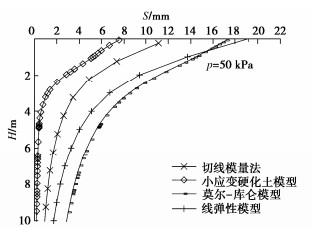
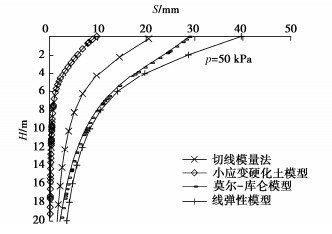
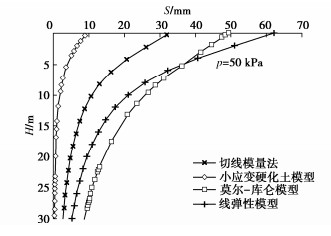
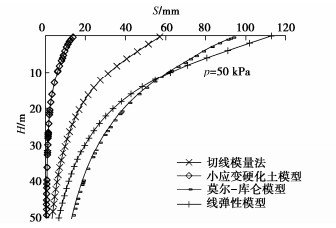
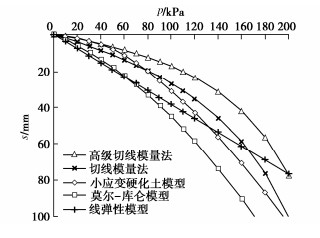
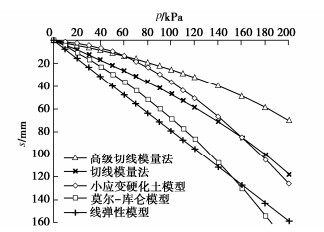
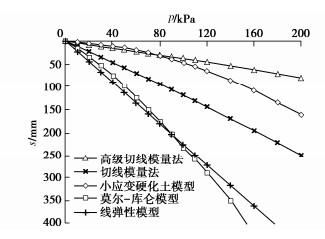
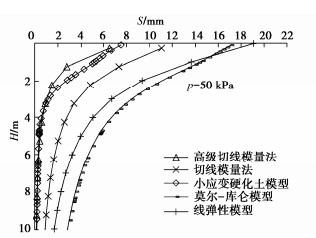
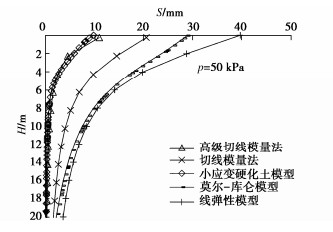
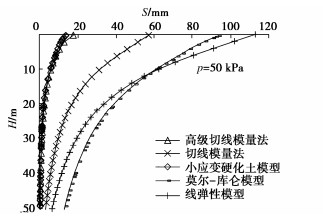
为比较不同基础尺寸的影响，现用PLAXIS 3D软件分别对尺寸为3 m×3 m，6 m×6 m，10 m×10 m，20 m×20 m压板地表位置的载荷试验进行模拟，其中压板仍采用2D板单元，弹性模量取1×10¹² kPa，厚度取2 m，由于基础尺寸改变，为更好表现土体沉降的非线性，计算荷载范围变为10~200 kPa，由于E_t0不随压板尺寸变化，故用切线模量法计算沉降时E_t0依旧采用14.61 MPa，计算结果仍旧考虑基础刚度，即最终结果乘以系数0.8，R_f取值都为1.0，计算所得基础底部中心点位置土体p–s曲线对比见图 5~8，当p=50 kPa时的H–S曲线对比见图 9~12。由上述图可见，当基础较大（10 m以上）时，切线模量法、莫尔-库仑模型以及线弹性模型计算所得最终沉降量相比小应变硬化土模型会偏大，且荷载影响深度也偏大。但且对于常规尺寸的基础（如6 m），切线模量法计算能取到比较好的效果。

图 5 各方法p–s曲线对比图(3 m×3 m)

Figure 5. Comparison of p–s curves by various methods (3 m×3 m)

下载: 全尺寸图片幻灯片

图 6 各方法p–s曲线对比图(6 m×6 m)

Figure 6. Comparison of p–s curves by various methods (6 m×6 m)

下载: 全尺寸图片幻灯片

图 7 各方法p–s曲线对比图(10 m×10 m)

Figure 7. Comparison of p–s curves by various methods (10 m×10 m)

下载: 全尺寸图片幻灯片

图 8 各方法p–s曲线对比图(20 m×20 m)

Figure 8. Comparison of p–s curves by various methods (20 m×20 m)

下载: 全尺寸图片幻灯片

图 9 各方法H–S曲线对比图(3 m×3 m)

Figure 9. Comparison of H–S curves by various methods (3 m×3 m)

下载: 全尺寸图片幻灯片

图 10 各方法H–S曲线对比图(6 m×6 m)

Figure 10. Comparison of H–S curves by various methods (6 m×6 m)

下载: 全尺寸图片幻灯片

图 11 各方法H–S曲线对比图(10 m×10 m)

Figure 11. Comparison of H–S curves by various methods (10 m×10 m)

下载: 全尺寸图片幻灯片

图 12 各方法H–S曲线对比图(20 m×20 m)

Figure 12. Comparison of H–S curves by various methods (20 m×20 m)

下载: 全尺寸图片幻灯片

以上结果表明，在土体沉降计算中，当基础尺寸较小时，荷载影响深度较浅，考虑E_t0随深度变化并不怎么影响计算结果，而当基础尺寸较大时，荷载影响深度大，如假定E_t0不变，计算所得最终沉降量相比小应变硬化土模型则偏大较多。因此考虑E_t0随深度变化的影响会更合理和符合实际。

2. 高级切线模量法

2.1 E_t0随深度变化的规律研究

由于小应变硬化土模型考虑了模量随深度的变化，为研究E_t0随深度变化的规律，以下采用有限元方法用小应变硬化土模型对该问题进行研究。研究思路为在不同深度做固定尺寸的压板试验，求得压板在不同埋深时底部中心点位置土体的p–s曲线，而后根据各p–s曲线计算不同深度土体的初始切线模量E_t0，以此研究E_t0沿深度变化的规律。

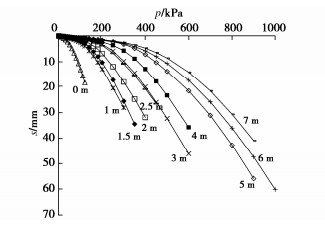
小应变硬化土模型参数用表 1给出的值。由于以上已计算出表层土的E_t0值，故只需计算位于深层时土体的E_t0值。试验步骤为将压板垂直向下平移nm，不考虑土体卸载的影响，对压板分级加载，按照计算0 m埋深时的方法依次计算1 m×1 m压板埋深为1~7 m的各情况，将所算得的所有p–s曲线绘制于1张图，见图 13。图中显示，压板埋置深度越深时，施加相同荷载时压板所产生的沉降则越小，在埋深为0 m时，在压板上方施加100 kPa的荷载，压板底部的沉降为13.18 mm，而在埋深为7 m时，就算施加100 kPa的荷载，压板底部沉降则很小。用以上的双曲线方程拟合各深度所得的p–s曲线，最后计算出E_t0随深度变化的值如表 4所示，绘制成图则见图 14。表 4 K₀的倒数即为a值，K₀相当于曲线的初始刚度。

图 13 压板在不同埋深处的荷载–沉降曲线

Figure 13. Load-settlement curves of plate at different buried depths

下载: 全尺寸图片幻灯片

图 14 不同埋深处的E_t0

Figure 14. E_t0 at different buried depths

下载: 全尺寸图片幻灯片

表 4 1 m×1 m压板E_t0随深度变化情况

Table 4. Variation of E_t0 of 1 m×1 m plate with buried depth

H/m	K₀	E_t0/MPa	a	b
0	18.25	14.61	0.0548	0.0056
1.0	28.82	23.08	0.0347	0.0022
1.5	32.15	25.75	0.0311	0.0020
2.0	39.84	31.90	0.0251	0.0018
2.5	46.73	37.42	0.0214	0.0014
3.0	48.08	38.50	0.0208	0.0013
4.0	54.95	44.00	0.0182	0.0013
5.0	61.73	49.43	0.0162	0.0009
6.0	64.52	51.66	0.0155	0.0008
7.0	69.93	56.00	0.0143	0.0007

下载: 导出CSV

| 显示表格

由表 4可得，b随深度增加逐渐减小，由于p_u=1/b，则p_u随深度的增加而增大，符合实际规律。E_t0也随深度的增加而变大，如图 14所示。

2.2 高级切线模量法

Mohr-Coulomb强度准则为

${\sigma _1} - {\sigma _3} = \frac{{2{\sigma _3}\sin \varphi + 2c}}{{1 - \sin \varphi }} {\rm{。}}$

(6)

强度随围压增大而增大，不同围压下，强度之比值为

$\frac{{{{({\sigma _1} - {\sigma _3})}_{{{\text{f}}_{\text{1}}}}}}}{{{{({\sigma _1} - {\sigma _3})}_{{{\text{f}}_{\text{2}}}}}}} = \frac{{{\sigma _{31}}\sin \varphi + c\cos \varphi }}{{{\sigma _{32}}\sin \varphi + c\cos \varphi }} {\rm{。}}$

(7)

E_t0的变化也类似为随围压增大而增大，参考Duncan-Chang模型和小应变硬化土模型，引入指数函数，提出E_t0随深度的变化关系式：

${E_{{\text{t0}}}} = {E'_{{\text{t}}0}}{\left( {\frac{{p + c\cot \varphi }}{{{p_0} + c\cot \varphi }}} \right)^m} {\rm{。}}$

(8)

式中p为要计算深度h处的土体自重应力，p= $\gamma h$ ； ${E'_{{\text{t}}0}}$ 为某深度h₀处已知的初始切线模量； ${p_0}$ 为初始自重应力，为 $\gamma {h_0}$ ，h₀为 ${E'_{{\text{t}}0}}$ 对应的深度；c为黏聚力， $\varphi$ 为内摩擦角，m为系数。当 ${E'_{{\text{t}}0}}$ 无实测数据时，可取2倍的变形模量E₀，据实例计算验证，此时对应的 ${p_0}$ 取20 kPa是一个较为合适的选择。对于砂土，c=0，又只有地表 ${E'_{{\text{t}}0}}$ 实测数据进而无法进行计算时，也可用p=20 kPa进行计算，即增大系数最小值为1。

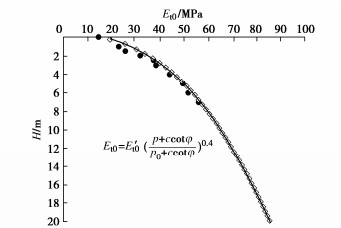
为确定式（8）中系数m的取值，现对图 14中E_t0与H的散点关系进行拟合，可以得到该工况下的系数m=0.4，拟合结果见图 15。

图 15 E_t0与H拟合图

Figure 15. Fitting of E_t0 and H

下载: 全尺寸图片幻灯片

根据以上考虑，切线模量法E_t计算式变为

${E_{\text{t}}} = {\left( {1 - {R_{\text{f}}}\frac{p}{{{p_{\text{u}}}}}} \right)^2}{\left( {\frac{{p + c\cot \varphi }}{{{p_0} + c\cot \varphi }}} \right)^m}{E'_{{\text{t}}0}}{\rm{。}}$

(9)

这就是地基沉降计算的高级切线模量法。该式参数少且物理意义明确，可以用压板试验确定，保证了参数的原位特性，又较好反映了土的非线性特性。

2.3 压板尺寸与m的关系研究

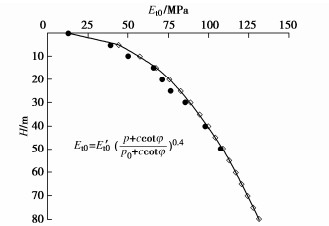
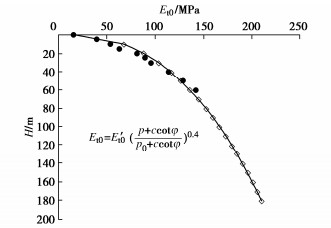
为讨论m与压板尺寸的关系，现进行压板尺寸分别为10 m×10 m、20 m×20 m的E_t0与H关系计算，并将m=0.4代入式（8）中与散点图进行对比，见图 16，17，图中显示，在压板尺寸不同时，拟合结果依旧比较接近，可以发现m的值与压板尺寸无关，是由土层的属性决定的。

图 16 E_t0与H拟合图(10 m×10 m)

Figure 16. Fitting of E_t0 and H (10 m×10 m)

下载: 全尺寸图片幻灯片

图 17 E_t0与H拟合图(20 m×20 m)

Figure 17. Fitting of E_t0 and H (20 m×20 m)

下载: 全尺寸图片幻灯片

3. 高级切线模量法与其他方法的对比

3.1 1 m×1 m压板的对比

为验证高级切线模量法的实用性，用以上的案例参数，计算1 m×1 m尺寸压板无埋深时底部中心点位置土体的p–s曲线以及H–S曲线，基础宽度b=1 m，埋深d=0 m，基础施加每级荷载增量为10 kPa，即 $\Delta p$ =10 kPa，分层厚度 $\Delta h$ =0.5 m，取每层土的中心点位置进行计算，计算深度h取10 m，可分为20层。以第一层荷载计算p=10 kPa为例说明计算过程。其中计算时选取的E_t0为由式（8）计算出的结果。

第一级荷载下，第一层土计算深度为 ${z_1} =$ $0.25{\text{ m}}$ ，附加应力系数K_c=0.9299，则该深度处附加应力 $\Delta {\sigma _{\text{1}}} = 9.299{\text{ kPa}}$ ， ${p_{\text{u}}} =$ ${\text{169}}{\text{.9 kPa}}$ （按 ${p_{\text{u}}} = c{N_c} +$ ${\gamma }_{0}d{N}_{q}+\frac{1}{2}\gamma b{N}_{\gamma }计算$ ）。

将h=0.25代入式（8）得该层土的切线模量，E_t0为19.38 MPa， ${E_{\text{t}}}_{\text{1}} = {\text{17}}{\text{.32 MPa}}$ 。则第一层的沉降为 $\Delta {s_1} = 0.27{\text{ mm}}$ 。

第二层土计算深度为 ${z_1} = 0.75{\text{ m}}$ ，附加应力系数K_c=0.4842，则该深度处附加应力 $\Delta {\sigma _{\text{2}}} = 4.84{\text{ kPa}}$ ， ${p_{\text{u}}} = {\text{258}}{\text{.5 kPa}}$ 。

该层土的切线模量 ${E_{\text{t}}}_{\text{2}} = {\text{24}}{\text{.69 MPa}}$ （此处h=0.75代入式（8），E_t0已变为25.64 MPa）。则第二层的沉降为 $\Delta {s_2} = 0.10{\text{ mm}}$ 。

以此类推，可求得每一层土的沉降值，将每一层土的沉降值叠加，可以在最终求得第一级荷载10 kPa下土体的最终沉降值 ${s_1} = 0.47{\text{ mm}}$ 。

同样对计算结果考虑基础刚性，乘以系数0.8，作为最终结果，即 ${s'_1} = 0.376{\text{ mm}}$ 。

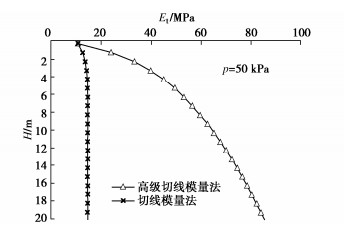
重复以上过程，可求得每级荷载下的沉降值，根据计算结果绘制该压板尺寸下的p–s曲线并与原切线模量法以及有限元各方法的计算结果进行对比，见图 18所示。当p=50 kPa时沉降s随深度H的变化情况对比见图 19，切线模量E_t随深度的变化对比见图 20。图中表明当压板尺寸为1 m×1 m时，用高级切线模量法计算的结果与原切线模量法差别不大，各级荷载计算得到的最终沉降量都比较接近有限元小应变硬化土模型得出的值，沉降S随深度H的变化情况也相差不大。虽然两种方法计算深层土的E_t时结果差别很大，但由于压板尺寸较小，荷载影响深度也较小，所以深部的E_t变化情况对计算结果影响并不大。

图 18 p–s曲线对比(1 m×1 m)

Figure 18. Comparison of p–s curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 19 H–S曲线对比(1 m×1 m)

Figure 19. Comparison of H–S curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 20 E_t–H曲线对比(1 m×1 m)

Figure 20. Comparison of E_t–H curves (1 m×1 m)

下载: 全尺寸图片幻灯片

3.2 其他尺寸基础的对比

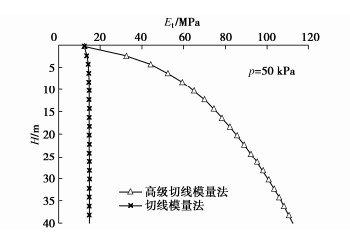
现同时对3 m×3 m、6 m×6 m、10 m×10 m、20 m×20 m尺寸基础的情况进行相同计算，可做出各尺寸压板底部中心点位置土体的p–s曲线对比，见图 21~24，当p=50 kPa时的H–S曲线对比见图 25~28，E_t随深度的变化对比见图 29~32。图中显示，在基础较大（6 m以上）的情况下用原切线模量法进行计算，以小应变硬化土模型的结果作为对比，荷载的影响深度与计算的最终沉降量都会偏大很多，而如用高级切线模量法计算，荷载影响深度与小应变硬化土模型则比较接近，计算得到的最终沉降量也是更接近小应变硬化土模型的值。所以在基础尺寸较大的情况下，用高级切线模量法计算沉降更能反映深层土体的变形趋势。

图 21 p–s曲线对比(3 m×3 m)

Figure 21. Comparison of p–s curves (3 m×3 m)

下载: 全尺寸图片幻灯片

图 22 p–s曲线对比图(6 m×6 m)

Figure 22. Comparison of p–s curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 23 p–s曲线对比(10 m×10 m)

Figure 23. Comparison of p–s curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 24 p–s曲线对比图(20 m×20 m)

Figure 24. Comparison of p–s curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 25 H–S曲线对比图(3 m×3 m)

Figure 25. H–S curve comparison (3 m×3 m)

下载: 全尺寸图片幻灯片

图 26 H–S曲线对比图(6 m×6 m)

Figure 26. Comparison of H–S curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 27 H–S曲线对比图(10 m×10 m)

Figure 27. Comparison of H–S curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 28 H–S曲线对比图(20 m×20 m)

Figure 28. Comparison of H–S curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 29 E_t–H曲线对比图(3 m×3 m)

Figure 29. Comparison of E_t–H curves (3 m×3 m)

下载: 全尺寸图片幻灯片

图 30 E_t–H曲线对比图(6 m×6 m)

Figure 30. Comparison of E_t–H curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 31 E_t–H曲线对比图(10 m×10 m)

Figure 31. Comparison of E_t–H curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 32 E_t–H曲线对比图(20 m×20 m)

Figure 32. Comparison of E_t–H curves (20 m×20 m)

下载: 全尺寸图片幻灯片

4. 工程实例验证

4.1 工程实例一

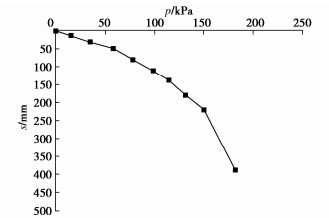
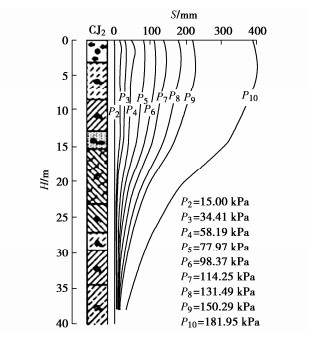
该工程^[8-9]为新建两座5×10⁴ m³油罐，对其中一座油罐（ST102油罐）进行试验研究，该油罐直径60 m，受充水荷载，在各级充水荷载下油罐中心点地表沉降情况如图 33所示。为分析油罐中心点在各级充水荷载下地基深层土的变形情况，以深层土实测变形S为横坐标，埋深H为纵坐标，绘制出在各级荷载下地基深层土的沉降实测曲线如图 34所示。

图 33 实测p–s曲线

Figure 33. Measured p–s curves

下载: 全尺寸图片幻灯片

图 34 不同充水荷载下H–S曲线

Figure 34. H–S curves under different water-filling loads

下载: 全尺寸图片幻灯片

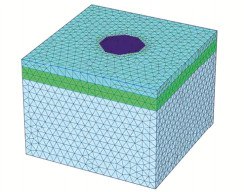
为方便计算，在计算时将土近似分为3层，第一层土为粉质黏土，厚度为12 m，第二层为淤泥质黏土，厚度为18 m，最下层为砂质粉土。土的基本力学性质见表 5，其中变形模量E₀是根据文献[5，10]所计算出的经验值。用有限元方法计算沉降时，莫尔-库仑模型以及线弹性模型参数取值见表 6，7，小应变硬化土模型参数取值见表 8，取E_oed=E₅₀=E₀，E_ur=3E₅₀，G₀= 1.5E_ur，一般取 ${\gamma _{0.7}}$ =2×10^-4。PLAXIS软件有限元模型见图 35，其中基础采用2D板单元，厚度为2 m，弹性模量取1×10¹² kPa。

表 5 土的基本力学参数

Table 5. Mechanical parameters of soil

土体名称	$\gamma$ /(kN·m^-3)	c/kPa	$\varphi$ /(°)	e	E_s1-2/MPa	E₀/MPa
粉质黏土	18.5	18.3	19.5	1.15	7.5	14
淤泥质黏土	17.6	7.5	5.8	1.20	3	4.1
砂质粉土	18.3	10	20	1	7.4	14

下载: 导出CSV

| 显示表格

表 6 莫尔-库仑模型参数取值

Table 6. Mechanical parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
粉质黏土	18.5	0.3	18.3	19.5	14
淤泥质黏土	17.6	0.3	7.5	5.8	4.1
砂质粉土	18.3	0.3	10	20	14

下载: 导出CSV

| 显示表格

表 7 线弹性模型参数取值

Table 7. Mechanical parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
粉质黏土	18.5	0.3	14
淤泥质黏土	17.6	0.3	4.1
砂质粉土	18.3	0.3	14

下载: 导出CSV

| 显示表格

表 8 小应变硬化土模型参数取值

Table 8. Mechanical parameters of soil for small-strain hardening model

土层	$\gamma$ /(kN·m^-3)	ν_ur	c/kPa	ϕ/(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
粉质黏土	18.50	0.2	18.3	19.5	0.6662	100	0.8	63.0	14	14.0	42.0	2×10^-4
淤泥质黏土	17.60	0.2	7.5	5.8	0.8989	100	0.8	18.1	4.1	4.1	12.3	2×10^-4
砂质粉土	18.30	0.2	10.0	20.0	0.6580	100	0.5	63.0	14	14.0	42.0	2×10^-4

下载: 导出CSV

| 显示表格

图 35 有限元模型图

Figure 35. Finite element model diagram

下载: 全尺寸图片幻灯片

用各方法计算基础中心点位置土体的p–s曲线，用切线模量法计算时，E_t0取2倍的变形模量E₀，不同的土层取的E_t0也不同。高级切线模量法不同深度的E_t0取值按式（8）计算， ${E'_{{\text{t}}0}}$ 取2E₀，p₀取20 kPa，m取0.3，其中下层土E_t0计算时不考虑上层土的影响，直接按深度计算，如计算淤泥质黏土层的分层沉降时，首先需确定计算层对应的深度，如20 m埋深处，再将该深度（h=20 m）对应的自重应力p和初始切线模量 ${E'_{{\text{t}}0}}$ 代入式（8），按参数c=7.5 kPa、 $\varphi$ =5.8°计算该深度处的E_t0。用两种切线模量法计算时，分层厚度为3 m一层，荷载按实测的分级方式分级，竖向应力按均质弹性解计算，计算各分层沉降，然后叠加，如3.1节所述，各土层R_f取值都为1.0。计算过程中，0~12 m深度的土层取 $\varphi$ =19.5°计算 ${N_\gamma }$ ， ${N_q}$ ， ${N_c}$ ，12~30 m深度的土层取 $\varphi$ =5.8°计算 ${N_\gamma }$ ， ${N_q}$ ， ${N_c}$ ，30 m以下深度的土层取 $\varphi$ =20°计算 ${N_\gamma }$ ， ${N_q}$ ， ${N_c}$ ，按照不同土层的E_t0分别计算不同深度土层的实际切线模量E_t，最终计算深度为200 m。

规范法计算沉降时，采用式（1）计算，分层厚度为每层6 m，计算深度为200 m，其中压缩模量采用表 5中的E_s1-2值，修正系数 ${\psi _{\text{s}}}$ 根据国家规范^[2]中规定取值，在p＜114.25 kPa时， ${\psi _{\text{s}}}$ 取0.7，当p≥114.25 kPa时， ${\psi _{\text{s}}}$ 取1.0。

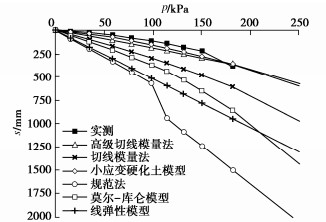
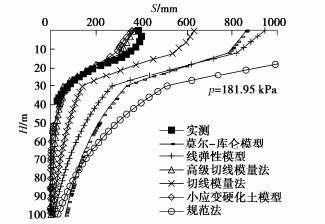
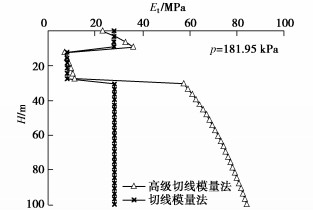
两种切线模量法以及规范法的最终沉降计算结果都考虑基础刚度影响，乘以系数0.8，最终得到的基础底部中心点位置土体p–s曲线对比如图 36所示，充水荷载为181.95 kPa时，不同方法计算的H–S曲线见图 37，两种切线模量法的E_t对比见图 38。图中显示，有限元小应变硬化土模型与高级切线模量法算出的结果近似，也最接近实测值。而其他方法计算的结果比实测值大较多，用来计算沉降则过于保守。

图 36 不同方法p–s曲线对比

Figure 36. Comparison of p–s curves of different methods

下载: 全尺寸图片幻灯片

图 37 不同方法H–S曲线对比图

Figure 37. Comparison of H–S curves by various methods

下载: 全尺寸图片幻灯片

图 38 E_t–H曲线对比图

Figure 38. Comparison of E_t–H curves by various methods

下载: 全尺寸图片幻灯片

4.2 工程实例二

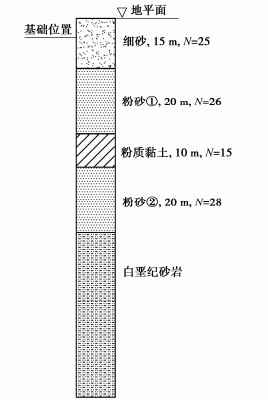
该项目^[11]是南非德班的海上游行假日酒店，从1982年中期开始规划建设，并于1985年4月开业。场地被海滩沉积物、夹层砂、港口河床的粉砂和粉质黏土以及地下约50~60 m处的白垩纪砂岩所覆盖，土层根据性质的不同可分为5层，地层简化图见，基本力学参数见，其中各参数取值依据如下：砂土内摩擦角 $\varphi$ 值是根据广东省《建筑地基基础设计规范》^[12]推荐的砂土标贯击数N值与内摩擦角 $\varphi$ 值关系式 $\varphi = \sqrt {20N} {\text{ + }}15$ 计算所得，变形模量E₀则根据文献[5]通过地基承载力反算得到，粉质黏土与白垩纪砂岩参数也据文献[5]通过地基承载力反算得到。

图 39 地层分布图

Figure 39. Distribution of soil strata

下载: 全尺寸图片幻灯片

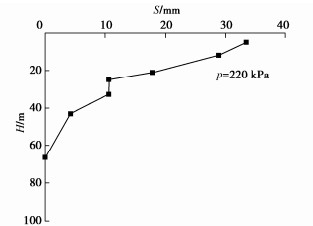
表 9 土的基本力学参数

Table 9. Mechanical parameters of soil

土体名称	$\gamma$ /(kN·m^-3)	c/kPa	$\varphi$ /(°)	E₀/MPa
细砂	18.5	0	37	44.4
粉砂①	18.5	0	38	48.7
粉质黏土	18.5	25	22	27.0
粉砂②	18.5	0	39	67.3
白垩纪砂岩	18.5	150	38	250.0

下载: 导出CSV

| 显示表格

基础设计时采用筏板基础，基础长68.5 m，宽36.4 m，厚度2 m，基础埋深为6.4 m，基础上总应力为220 kPa，基础底部中心点位置土体最终沉降量为33.4 mm，测得土体沉降S随埋深H变化的规律如图 40所示。

图 40 实测H–S曲线

Figure 40. Measured H–S curves

下载: 全尺寸图片幻灯片

用有限元方法计算土体沉降时，莫尔-库仑模型以及线弹性模型参数取值见表 10，11，其中莫尔-库仑模型与线弹性模型的模量取变形模量，小应变硬化土模型参数取值见表 12。PLAXIS建模见图 41，基础采用2D板单元，厚度为2 m，弹性模量取1×10¹² kPa。计算时施工步骤分为3步：①初始应力场分析；②开挖并位移清零；③加载。

表 10 莫尔-库仑模型参数取值

Table 10. Parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
细砂	18.5	0.3	0	37	44.4
粉砂①	18.5	0.3	0	38	48.7
粉质黏土	18.5	0.3	25	22	27.0
粉砂②	18.5	0.3	0	39	67.3
白垩纪砂岩	18.5	0.3	150	38	250.0

下载: 导出CSV

| 显示表格

表 11 线弹性模型参数取值

Table 11. Parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
细砂	18.5	0.3	44.4
粉砂①	18.5	0.3	48.7
粉质黏土	18.5	0.3	27.0
粉砂②	18.5	0.3	67.3
白垩纪砂岩	18.5	0.3	250.0

下载: 导出CSV

| 显示表格

表 12 小应变硬化土模型参数取值

Table 12. Parameters of soil for small-strain hardening model

土层	$\gamma$ /(kN·m^-3)	${\nu _{{\text{ur}}}}$	c/kPa	$\varphi$ /(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
细砂	18.5	0.2	0	37	0.398	100	0.5	199.8	44.4	44.4	133.2	2×10^-4
粉砂①	18.5	0.2	0	38	0.384	100	0.5	438.3	48.7	48.7	146.1	2×10^-4
粉质黏土	18.5	0.2	25	22	0.625	100	0.8	121.5	27.7	27.7	81.0	2×10^-4
粉砂②	18.5	0.2	0	39	0.371	100	0.5	302.8	67.3	67.3	201.9	2×10^-4
白垩纪砂岩	18.5	0.2	150	38	0.384	100	0.5	1125.0	250	250	750.0	2×10^-4

下载: 导出CSV

| 显示表格

图 41 有限元模型图

Figure 41. Diagram of finite element model

下载: 全尺寸图片幻灯片

用切线模量法计算时，E_t0取2倍的变形模量E₀，高级切线模量法不同深度E_t0取值按式（8）计算，其中 ${E'_{{\text{t}}0}}$ 取2E₀，p₀取20 kPa，m取0.3，下层土E_t0计算时不考虑上层土的影响，直接按深度计算，分层厚度为5 m一层，荷载分5级加载，每级为44 kPa，总荷载为220 kPa，各土层R_f取值都为1.0，按照不同土层的E_t0分别计算不同深度土层的实际切线模量E_t，最终计算深度则为200 m，两种方法考虑基础刚度乘系数0.8，计算得出基础底部中心点位置土体沉降量分别为82.32，36.21 mm。

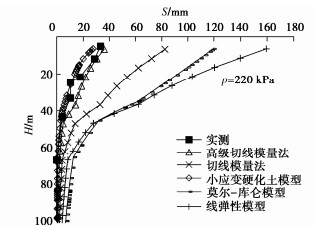
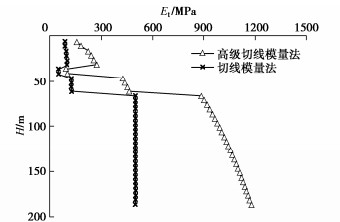
不同方法计算的H–S曲线见图 42，两种切线模量法的E_t对比见图 43。图中显示，小应变硬化土模型与高级切线模量法算出的结果较接近实测值，而其他方法计算的结果比实测值大较多，进一步证明了高级切线模量法的实用性。

图 42 不同方法H–S曲线对比图

Figure 42. Comparison of H–S curves by various methods

下载: 全尺寸图片幻灯片

图 43 E_t–H曲线对比图

Figure 43. Comparison of E_t–H curves by various methods

下载: 全尺寸图片幻灯片

5. 结论

本文在切线模量法的基础上，提出了考虑初始切线模量沿深度增加的高级切线模量法，通过用小应变硬化土模型数值方法探究E_t0随深度的变化参数m。主要得出3点结论。

（1）用切线模量法计算最终沉降量时，对于常规尺寸，如小于6 m的基础来说影响不大，能够取得较好的效果。

（2）对于边长大于10 m这样大尺寸的筏板基础，当计算深度较深时，常规切线模量法计算出的沉降量偏大。

（3）初步的应用表明，考虑初始切线模量沿深度增加的高级切线模量法是更合理的地基沉降计算方法，结果与小应变硬化土模型和实测值比较接近。同时，该法简单方便，参数少且物理意义明确，易确定，更好地反映了土的非线性变形特性，可以方便地用原位试验确定参数，使确定的参数能反映原位土的特性，保证了参数的可靠性，为地基沉降计算提供了先进可靠而又非常简单的方法，是很值得发展完善的方法。

如何针对不同土，更合理地确定高级切线模量法中初始切线模量指数m还需进一步地研究探讨，并需要更多的工程验证。

图 1 各模型计算所得p–s曲线

Figure 1. p–s curves calculated by various models

下载: 全尺寸图片幻灯片

图 2 s与s/p拟合曲线

Figure 2. Fitting curves of s and s/p

下载: 全尺寸图片幻灯片

图 3 各方法p–s曲线对比图(1 m×1 m)

Figure 3. Comparison of p–s curves by various methods (1 m×1 m)

下载: 全尺寸图片幻灯片

图 4 各方法H–S曲线对比图(1 m×1 m)

Figure 4. Comparison of H–S curves by various methods (1 m×1 m)

下载: 全尺寸图片幻灯片

图 5 各方法p–s曲线对比图(3 m×3 m)

Figure 5. Comparison of p–s curves by various methods (3 m×3 m)

下载: 全尺寸图片幻灯片

图 6 各方法p–s曲线对比图(6 m×6 m)

Figure 6. Comparison of p–s curves by various methods (6 m×6 m)

下载: 全尺寸图片幻灯片

图 7 各方法p–s曲线对比图(10 m×10 m)

Figure 7. Comparison of p–s curves by various methods (10 m×10 m)

下载: 全尺寸图片幻灯片

图 8 各方法p–s曲线对比图(20 m×20 m)

Figure 8. Comparison of p–s curves by various methods (20 m×20 m)

下载: 全尺寸图片幻灯片

图 9 各方法H–S曲线对比图(3 m×3 m)

Figure 9. Comparison of H–S curves by various methods (3 m×3 m)

下载: 全尺寸图片幻灯片

图 10 各方法H–S曲线对比图(6 m×6 m)

Figure 10. Comparison of H–S curves by various methods (6 m×6 m)

下载: 全尺寸图片幻灯片

图 11 各方法H–S曲线对比图(10 m×10 m)

Figure 11. Comparison of H–S curves by various methods (10 m×10 m)

下载: 全尺寸图片幻灯片

图 12 各方法H–S曲线对比图(20 m×20 m)

Figure 12. Comparison of H–S curves by various methods (20 m×20 m)

下载: 全尺寸图片幻灯片

图 13 压板在不同埋深处的荷载–沉降曲线

Figure 13. Load-settlement curves of plate at different buried depths

下载: 全尺寸图片幻灯片

图 14 不同埋深处的E_t0

Figure 14. E_t0 at different buried depths

下载: 全尺寸图片幻灯片

图 15 E_t0与H拟合图

Figure 15. Fitting of E_t0 and H

下载: 全尺寸图片幻灯片

图 16 E_t0与H拟合图(10 m×10 m)

Figure 16. Fitting of E_t0 and H (10 m×10 m)

下载: 全尺寸图片幻灯片

图 17 E_t0与H拟合图(20 m×20 m)

Figure 17. Fitting of E_t0 and H (20 m×20 m)

下载: 全尺寸图片幻灯片

图 18 p–s曲线对比(1 m×1 m)

Figure 18. Comparison of p–s curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 19 H–S曲线对比(1 m×1 m)

Figure 19. Comparison of H–S curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 20 E_t–H曲线对比(1 m×1 m)

Figure 20. Comparison of E_t–H curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 21 p–s曲线对比(3 m×3 m)

Figure 21. Comparison of p–s curves (3 m×3 m)

下载: 全尺寸图片幻灯片

图 22 p–s曲线对比图(6 m×6 m)

Figure 22. Comparison of p–s curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 23 p–s曲线对比(10 m×10 m)

Figure 23. Comparison of p–s curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 24 p–s曲线对比图(20 m×20 m)

Figure 24. Comparison of p–s curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 25 H–S曲线对比图(3 m×3 m)

Figure 25. H–S curve comparison (3 m×3 m)

下载: 全尺寸图片幻灯片

图 26 H–S曲线对比图(6 m×6 m)

Figure 26. Comparison of H–S curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 27 H–S曲线对比图(10 m×10 m)

Figure 27. Comparison of H–S curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 28 H–S曲线对比图(20 m×20 m)

Figure 28. Comparison of H–S curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 29 E_t–H曲线对比图(3 m×3 m)

Figure 29. Comparison of E_t–H curves (3 m×3 m)

下载: 全尺寸图片幻灯片

图 30 E_t–H曲线对比图(6 m×6 m)

Figure 30. Comparison of E_t–H curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 31 E_t–H曲线对比图(10 m×10 m)

Figure 31. Comparison of E_t–H curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 32 E_t–H曲线对比图(20 m×20 m)

Figure 32. Comparison of E_t–H curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 33 实测p–s曲线

Figure 33. Measured p–s curves

下载: 全尺寸图片幻灯片

图 34 不同充水荷载下H–S曲线

Figure 34. H–S curves under different water-filling loads

下载: 全尺寸图片幻灯片

图 35 有限元模型图

Figure 35. Finite element model diagram

下载: 全尺寸图片幻灯片

图 36 不同方法p–s曲线对比

Figure 36. Comparison of p–s curves of different methods

下载: 全尺寸图片幻灯片

图 37 不同方法H–S曲线对比图

Figure 37. Comparison of H–S curves by various methods

下载: 全尺寸图片幻灯片

图 38 E_t–H曲线对比图

Figure 38. Comparison of E_t–H curves by various methods

下载: 全尺寸图片幻灯片

图 39 地层分布图

Figure 39. Distribution of soil strata

下载: 全尺寸图片幻灯片

图 40 实测H–S曲线

Figure 40. Measured H–S curves

下载: 全尺寸图片幻灯片

图 41 有限元模型图

Figure 41. Diagram of finite element model

下载: 全尺寸图片幻灯片

图 42 不同方法H–S曲线对比图

Figure 42. Comparison of H–S curves by various methods

下载: 全尺寸图片幻灯片

图 43 E_t–H曲线对比图

Figure 43. Comparison of E_t–H curves by various methods

下载: 全尺寸图片幻灯片

表 1 有限元小应变硬化土模型参数取值

Table 1 Mechanical parameter of soil for small strain hardened model

土层	$\gamma$ /(kN·m^-3)	${\nu _{{\text{ur}}}}$	c/kPa	$\varphi$ /(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
伦敦黏土	18.44	0.2	2	24	0.59	100	0.5	40	6.73	8	16	9.68×10^-4

下载: 导出CSV

表 2 莫尔-库仑模型参数取值

Table 2 Mechanical parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
伦敦黏土	18.44	0.3	2	24	7.3

下载: 导出CSV

表 3 线弹性模型参数取值

Table 3 Mechanical parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
伦敦黏土	18.44	0.3	7.3

下载: 导出CSV

表 4 1 m×1 m压板E_t0随深度变化情况

Table 4 Variation of E_t0 of 1 m×1 m plate with buried depth

H/m	K₀	E_t0/MPa	a	b
0	18.25	14.61	0.0548	0.0056
1.0	28.82	23.08	0.0347	0.0022
1.5	32.15	25.75	0.0311	0.0020
2.0	39.84	31.90	0.0251	0.0018
2.5	46.73	37.42	0.0214	0.0014
3.0	48.08	38.50	0.0208	0.0013
4.0	54.95	44.00	0.0182	0.0013
5.0	61.73	49.43	0.0162	0.0009
6.0	64.52	51.66	0.0155	0.0008
7.0	69.93	56.00	0.0143	0.0007

下载: 导出CSV

表 5 土的基本力学参数

Table 5 Mechanical parameters of soil

土体名称	$\gamma$ /(kN·m^-3)	c/kPa	$\varphi$ /(°)	e	E_s1-2/MPa	E₀/MPa
粉质黏土	18.5	18.3	19.5	1.15	7.5	14
淤泥质黏土	17.6	7.5	5.8	1.20	3	4.1
砂质粉土	18.3	10	20	1	7.4	14

下载: 导出CSV

表 6 莫尔-库仑模型参数取值

Table 6 Mechanical parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
粉质黏土	18.5	0.3	18.3	19.5	14
淤泥质黏土	17.6	0.3	7.5	5.8	4.1
砂质粉土	18.3	0.3	10	20	14

下载: 导出CSV

表 7 线弹性模型参数取值

Table 7 Mechanical parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
粉质黏土	18.5	0.3	14
淤泥质黏土	17.6	0.3	4.1
砂质粉土	18.3	0.3	14

下载: 导出CSV

表 8 小应变硬化土模型参数取值

Table 8 Mechanical parameters of soil for small-strain hardening model

土层	$\gamma$ /(kN·m^-3)	ν_ur	c/kPa	ϕ/(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
粉质黏土	18.50	0.2	18.3	19.5	0.6662	100	0.8	63.0	14	14.0	42.0	2×10^-4
淤泥质黏土	17.60	0.2	7.5	5.8	0.8989	100	0.8	18.1	4.1	4.1	12.3	2×10^-4
砂质粉土	18.30	0.2	10.0	20.0	0.6580	100	0.5	63.0	14	14.0	42.0	2×10^-4

下载: 导出CSV

表 9 土的基本力学参数

Table 9 Mechanical parameters of soil

土体名称	$\gamma$ /(kN·m^-3)	c/kPa	$\varphi$ /(°)	E₀/MPa
细砂	18.5	0	37	44.4
粉砂①	18.5	0	38	48.7
粉质黏土	18.5	25	22	27.0
粉砂②	18.5	0	39	67.3
白垩纪砂岩	18.5	150	38	250.0

下载: 导出CSV

表 10 莫尔-库仑模型参数取值

Table 10 Parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
细砂	18.5	0.3	0	37	44.4
粉砂①	18.5	0.3	0	38	48.7
粉质黏土	18.5	0.3	25	22	27.0
粉砂②	18.5	0.3	0	39	67.3
白垩纪砂岩	18.5	0.3	150	38	250.0

下载: 导出CSV

表 11 线弹性模型参数取值

Table 11 Parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
细砂	18.5	0.3	44.4
粉砂①	18.5	0.3	48.7
粉质黏土	18.5	0.3	27.0
粉砂②	18.5	0.3	67.3
白垩纪砂岩	18.5	0.3	250.0

下载: 导出CSV

表 12 小应变硬化土模型参数取值

Table 12 Parameters of soil for small-strain hardening model

土层	$\gamma$ /(kN·m^-3)	${\nu _{{\text{ur}}}}$	c/kPa	$\varphi$ /(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
细砂	18.5	0.2	0	37	0.398	100	0.5	199.8	44.4	44.4	133.2	2×10^-4
粉砂①	18.5	0.2	0	38	0.384	100	0.5	438.3	48.7	48.7	146.1	2×10^-4
粉质黏土	18.5	0.2	25	22	0.625	100	0.8	121.5	27.7	27.7	81.0	2×10^-4
粉砂②	18.5	0.2	0	39	0.371	100	0.5	302.8	67.3	67.3	201.9	2×10^-4
白垩纪砂岩	18.5	0.2	150	38	0.384	100	0.5	1125.0	250	250	750.0	2×10^-4

下载: 导出CSV

参考文献(12)

[1]	王海波, 徐明, 宋二祥. 基于硬化土模型的小应变本构模型研究[J]. 岩土力学, 2011, 32(1): 39–43, 136. doi: 10.3969/j.issn.1000-7598.2011.01.007 WANG Hai-bo, XU Ming, SONG Er-xiang. A small strain constitutive model based on hardening soil model[J]. Rock and Soil Mechanics, 2011, 32(1): 39–43, 136. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.01.007
[2]	建筑地基基础设计规范: GB 50007—2011[S]. 2012. Code for Design of Building Foundation: GB 50007—2011[S]. 2012. (in Chinese)
[3]	杨光华. 地基非线性沉降计算的原状土切线模量法[J]. 岩土工程学报, 2006, 28(11): 1927–1931. doi: 10.3321/j.issn:1000-4548.2006.11.002 YANG Guang-hua. Nonlinear settlement computation of the soil foundation with the undisturbed soil tangent modulus method[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1927–1931. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.11.002
[4]	杨光华, 王俊辉. 地基非线性沉降计算原状土切线模量法的推广和应用[J]. 岩土力学, 2011, 32(增刊1): 33–37. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1007.htm YANG Guang-hua, WANG Jun-hui. Application of undisturbed soil tangent modulus method for computing nonlinear settlement of soil foundation[J]. Rock and Soil Mechanics, 2011, 32(S1): 33–37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1007.htm
[5]	杨光华. 根据经验地基承载力反算土的强度和变形参数[J]. 广东水利水电, 2002(1): 3–6. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200201000.htm YANG Guang-hua. According to the experience of foundation bearing capacity to inverse the strength and deformation parameters of soil[J]. Guangdong Water Resources and Hydropower, 2002(1): 3–6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200201000.htm
[6]	杨光华. 深基坑支护结构的实用计算方法及其应用[M]. 北京: 地质出版社, 2004. YANG Guang-hua. Practical Calculation Method of Retaining Structures for Deep Excavations and Its Application[M]. Beijing: Geological Publishing House, 2004. (in Chinese)
[7]	DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(5): 1629–1653. doi: 10.1061/JSFEAQ.0001458
[8]	赵同顺, 周波. 大型油罐地基变形特性的研究[J]. 岩石力学与工程学报, 2004, 23(6): 1037–1043. doi: 10.3321/j.issn:1000-6915.2004.06.028 ZHAO Tong-shun, ZHOU Bo. Deformation behaviors of soft foundation under large oil tank[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(6): 1037–1043. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.06.028
[9]	赵同顺. 5×10⁴ m³大型油罐岩土工程实录[C]// 第五届全国岩土工程实录交流会岩土工程实录集, 2000, 南京. ZHAO Tong-shun. Geotechnical engineering record of 5×10⁴m³ large oil tank[C]// The 5th National Geotechnical Engineering Record Exchange Conference, 2000, Nanjing. (in Chinese)
[10]	舒武堂, 李国胜, 蒋涛. 武汉地区淤泥质软土、黏性土的压缩模量与变形模量的相关关系[J]. 岩土工程界, 2004, 7(7): 29–30. https://www.cnki.com.cn/Article/CJFDTOTAL-YSJS200407011.htm SHU Wu-tang, LI Guo-sheng, JIANG Tao. The correlativity between the compression model and elastic model for silt and clay in Wuhan[J]. Geotechnical Engineering World, 2004, 7(7): 29–30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSJS200407011.htm
[11]	C M PLANT G W. The settlement performance of a raft supporting a 27-storey hotel on estuarine deposits in Durban[J]. Civil Engineering = Siviele Ingenieurswese, 1990, 32(6).
[12]	建筑地基基础设计规范: DBJ15—31—2016[S]. 2016. Design Code for Building Foundation: DBJ15—31— 2016[S]. 2016. (in Chinese)

施引文献(14)

期刊类型引用(9)

1.	赵程斌，骆亚生，王博，齐国庆，孙哲，范全. 复杂参数条件下基于空间应力解的重塑黄土沉降计算方法. 人民黄河. 2024(03): 136-142 . 百度学术
2.	李兴余，沈春杨，陶雄武，张烜梓，胡小平，舒岳水. 220 kV变电站场地地基单桩沉降时间效应数值模拟. 华南地震. 2024(01): 149-156 . 百度学术
3.	李燕波. 非黏性碾压土石坝沉降计算探讨. 水利技术监督. 2024(06): 78-82 . 百度学术
4.	杜赐阳，高翔，苏阳，赵佳烁. 桂林素填土地基沉降变形及数值模拟研究. 山西建筑. 2024(16): 79-82+95 . 百度学术
5.	初欣雨，王学谦，闫秀英，郭鑫，李金龙. 地下超深基坑开挖工况下的周围土体沉降控制技术研究. 粘接. 2024(10): 157-159+164 . 百度学术
6.	丁祥，夏浩衍，龚坚刚，周奇，曹枚根. 杆塔基础沉降对输电塔线体系风振响应的影响研究. 浙江电力. 2023(03): 95-102 . 百度学术
7.	贺敏，郭卡都，曹文贵，欧蔓丽. 条形基础作用下粗粒土地基沉降计算改进方法. 人民长江. 2023(10): 170-176 . 百度学术
8.	杨光华. 确定地基承载力的p-s曲线法. 地基处理. 2022(02): 91-98 . 百度学术
9.	乔承杰. 应用切线模量法计算天然地基沉降的探讨. 地基处理. 2022(05): 394-399 . 百度学术