Influences of thermo-mechanical properties of clay on mechanical responses of energy piles
-
摘要: 能量桩运行会导致土体温度场的改变,从而影响桩周土的热–力学特性,进而影响能量桩的变形、桩–土界面应力及承载性能。将ACMEG-T土体热本构模型在ABAQUS软件中进行二次开发,通过编写UMAT子程序对能够反映黏土热–力耦合特性的三轴试验结果进行模拟与分析,验证了模型的可靠性。建立数值模型,研究了土体热–力学特性对能量桩位移、桩–土界面应力及桩身轴力的影响规律。研究结果表明,温度变化会导致土体产生累计沉降,并进一步导致桩侧产生负摩阻力;在负摩阻力的影响下,能量桩会产生额外的沉降以及不可恢复的轴力;土体热–力学特性对能量桩力学特性的影响效应随着土体超固结比的增加逐渐减弱。Abstract: Under the action of temperature variation induced by energy piles, the mechanical properties of soils surrounding the piles will be changed, thereby affecting their deformation, the stress of the pile-soil interface and the bearing capacity of the pile foundation. The ACMEG-T constitutive model for the thermal properties of soils is developed in ABAQUS commercial software. The accuracy of the program is verified by simulating the triaxial test results by using the UMAT subroutine. Based on the numerical simulation, the influence of thermo-mechanical properties of soils on the displacement of pile head, the stress of the pile-soil interface and the axial force of the energy piles in clay are studied. The results show that the change of soil temperature can lead to irretrievable settlement of soils, and further lead to negative skin friction on the pile shaft. The additional settlement and irreversible change of axial force of the energy piles can be induced by the negative skin friction. With the increase of the over-consolidation ratio of clay, the effects of thermo-mechanical properties of soils on the mechanical response of the energy piles decrease.
-
Keywords:
- energy pile /
- clay /
- constitutive model /
- over-consolidation ratio /
- numerical simulation
-
0. 引言
能量桩(又称能源桩)是将传统桩基与地埋式换热管相结合的新型桩基技术,具有支撑上部荷载与浅层地温能热交换的双重作用[1-2]。能量桩换热过程中,一般桩体温度变化范围为10℃~15℃[3],这会导致桩周土体的温度场发生变化,并进一步引起土体(尤其是黏土)力学性质的改变,进而影响桩基变形和承载性能。已开展的研究表明,温度变化会引起黏土的体积应变,尤其对于正常固结黏土及弱超固结(OCR)黏土,温度升高会导致土体产生体积压缩应变[4-5]。
为了分析温度对黏土力学性质的影响,相关学者针对黏土的热本构模型展开积极探索。Hueckel等[6]将温度作为状态变量引入相容方程,基于修正剑桥模型建立了可以考虑边界面热收缩和土体超固结比的土体热-弹塑性本构模型(MCC)。然而,MCC模型并不能很好反映超固结比对黏土力学特性的影响。Cui等[7]基于MCC模型理论框架,通过引入一个屈服面的热影响参数,使得模型能够考虑不同超固结比时温度变化引起的土体热塑性应变。姚仰平等[8-9]基于修正剑桥模型及临界状态理论,建立了一种简单、实用的三维超固结土弹塑性本构模型(UH),并通过引入温度参数考虑了温度对土体应力应变特性的影响,UH模型与其他模型相比最大的优点就是参数选取与修正剑桥模型一致。Zhou等[10]基于边界面理论提出一种可以考虑土体超固结比、边界面热收缩及边界面内部的弹塑性变化的热–力耦合本构模型,能较好反映土体小应变时的弹塑性变化。程晓辉等[11]、陈志辉等[12]基于颗粒熵运动和弹性弛豫等机制,建立了一种非平衡态的热–力学本构模型,该模型不同于传统弹塑性模型框架,能够更深入描述土体的变形和能量耗散机理。Laloui等[13-14]基于边界面理论,提出了一种适用于环境岩土工程相关热–力耦合问题的土体热本构模型(ACMEG-T),该模型能够较好地反映土体的热塑性应变特性及循环加卸载响应。
为了实现土体热本构模型在能源地下结构中的应用,部分学者在有限元软件中对土体热本构模型进行了二次开发[15-17],但其在能量桩热–力特性研究方面的应用仍相对较少。费康等[15]通过编写用户子程序将Zhou等[10]提出的热–力耦合本构模型导入了数值软件Abaqus中,对正常固结地基中不同桩顶荷载等级作用下的能量桩承载性能进行了研究,结果表明能量桩桩顶累积沉降与工作荷载及循环次数成正相关。Di等[16]通过将ACMEG-T模型[13-14]嵌入Lagamine软件中,对循环温度作用下黏土地基中能量桩单桩和群桩的热–力学特性进行了研究。土体的热–力学特性会受到超固结比的影响,因此黏土的超固结比也会对能量桩的力学特性造成影响。然而,上述研究并未考虑黏土超固结比对能量桩力学特性的影响。
ACMEG-T模型基于边界面理论,模型参数少,能更方便地实现其在有限元软件中的二次开发[18]。为了进一步探究不同超固结比条件下黏土地基中能量桩的热–力学响应特性,本文基于Abaqus软件的UMAT子程序功能,对ACMEG-T本构模型进行了二次开发,基于建立的数值模型,研究了不同超固结比条件下,土体的热–力学特性对能量桩位移、桩–土界面应力及桩身轴力的影响机制。研究结果有助于进一步揭示黏土地基中能量桩的工作特性及桩–土相互作用机理。
1. ACMEG-T热本构模型简介
1.1 弹塑性应变增量理论
根据弹塑性理论,总的应变增量可以分为弹性应变增量$ {\text{d}}{\varepsilon ^{{\text{Te}}}} + {\text{d}}{\varepsilon ^{{\text{me}}}} $和塑性应变增量$ {\text{d}}{\varepsilon ^{\text{p}}} $两部分;其中,弹性应变增量可分为温度引起$ {\text{d}}{\varepsilon ^{{\text{Te}}}} $和应力引起$ {\text{d}}{\varepsilon ^{{\text{me}}}} $的两类弹性应变增量:
$$ {\text{d}}\varepsilon = {\text{d}}{\varepsilon ^{{\text{Te}}}} + {\text{d}}{\varepsilon ^{{\text{me}}}} + {\text{d}}{\varepsilon ^{\text{p}}} 。 $$ (1) 1.2 温度对前期固结应力的影响
已有温控三轴试验结果表明,黏土受热后正常固结线会朝着孔隙比减小的方向移动[19]。因此,前期固结应力与体积应变及温度的关系为
$$ {P_{\text{c}}}^\prime = {P_{{\text{c0}}}}^\prime \exp (\beta \varepsilon _{\text{v}}^{\text{p}}) 。 $$ (2) 引入一种对数关系式来考虑温度对于前期固结应力的影响[14]:
$$ {p'_{{\text{c}}0}} = {p'_{{\text{c}}0{T_0}}}[1 - {\gamma _{\text{T}}} \cdot \ln (T/{T_0})] 。 $$ (3) 式中$ {p'_{\text{c}}} $为土体前期固结应力;$ {p'_{{\text{c}}0}} $,$ {p'_{{\text{c}}0{T_0}}} $分别为在温度T时刻或参考温度$ {T_0} $时刻的前期固结应力;$ \beta $为塑性指数($ \beta = (1 + {e_0})/(\lambda - k) $);$ \varepsilon _{\text{v}}^{\text{p}} $为塑性体积应变;$ {\gamma _{\text{T}}} $为材料参数。
结合式(2),(3),前期固结应力在温度作用下的表达式为
$$ {p'_{\text{c}}} = {p'_{{\text{c}}0{T_0}}}\exp (\beta \varepsilon _{\text{v}}^{\text{p}})[1 - {\gamma _{\text{T}}} \cdot \ln (T/{T_0})] 。 $$ (4) 1.3 温度对临界状态参数的影响
临界状态参数$ M $为$ p - q $平面临界状态线斜率,根据Cekerevac等[19]的相关研究结果,$ M $随温度的变化规律为
$$ M = {M_0} - g(T - {T_0}){\kern 1pt} \text{,} $$ (5) $$ {M_0} = \frac{{6\sin \varphi '}}{{3 - \sin \varphi '}} 。 $$ (6) 式中$ {M_0} $为参考温度$ {T_0} $时的临界状态线斜率;g为临界状态线斜率随温度的变化系数;$ \varphi ' $为临界状态内摩擦角。
1.4 模型屈服极限与塑性因子
塑性响应通过两种耦合机理表达,一种是等应力机理,另一种是偏应力机理,其屈服极限为分别为[14]
$$ {f_{{\text{iso}}}} = p' - {p'_{\text{c}}}{r_{{\text{iso}}}} = 0\text{,} $$ (7) $$ {f_{{\text{dev}}}} = q - Mp'\left[ {1 - b\ln \left( {\frac{{{\text{d}} \cdot p'}}{{{{p'}_{\text{c}}}}}} \right)} \right]{r_{{\text{dev}}}} = 0。 $$ (8) 式中b和d为材料参数;$ {r_{{\text{iso}}}} $和$ {r_{{\text{dev}}}} $分别为等应力屈服面和偏应力屈服面的塑性因子,分别对应两种机理的塑性调动程度。
参数$ {r_{{\text{iso}}}} $的存在使得ACMEG-T土体热本构模型能够反映等应力屈服面中土体塑性调动程度的变化,这使得等应力屈服机理能够反映土体的循环加卸载特性。基于边界面理论引入的此类概念,可以使得非线性$ e - \ln p $曲线在模型中尽可能平滑地变化。这种方法的基本理念就是通过使塑性模量与应力状态点到边界面投影点(投影中心点取应力空间零点)的距离成反比,从而使得应力状态点位于边界面上或边界面内时依然能够产生塑性应变[15]。在正常加载曲线上,$ {r_{{\text{iso}}}} $与等应力塑性体积应变呈双曲线关系:
$$ {r_{{\text{iso}}}} = r_{{\text{iso}}}^{\text{e}} + \frac{{\varepsilon _{\text{v}}^{{\text{p, iso}}}}}{{c + \varepsilon _{\text{v}}^{{\text{p, iso}}}}} 。 $$ (9) 在卸载及再加载阶段,$ {r_{{\text{iso}}}} $随着平均有效应力的减小而减小,随着循环体积应变的增加而增加:
$$ {r_{{\text{iso}}}} = r_{iso}^e + \frac{{{{p'}_{{\text{cyc}}}}}}{{{{p'}_{\text{c}}}}}{\text{ + }}\frac{{\varepsilon _{\text{v}}^{{\text{p, cyc, iso}}}}}{{c + \varepsilon _{\text{v}}^{{\text{p, cyc, iso}}}}} \leqslant 1。 $$ (10) 式中$ {p'_{{\text{cyc}}}} $为最后一次加卸载变化时的有效应力;$ \varepsilon _{\text{v}}^{{\text{p, iso}}} $为等应力塑性体积应变;$ \varepsilon _{\text{v}}^{{\text{p, cyc, iso}}} $为最后一次加卸载变化后累计产生的等应力塑性体积应变;$ r_{{\text{iso}}}^{\text{e}} $和c分别为定义弹性核大小和$ {r_{{\text{iso}}}} $变化规律的材料参数。
参数$ {r_{{\text{dev}}}} $与参数$ {r_{{\text{iso}}}} $的作用机理相同,使得偏应力屈服机理能够反应弹塑性变化过程,其变化为
$$ {r_{{\text{dev}}}} = r_{{\text{dev}}}^{\text{e}} + \frac{{\varepsilon _{\text{d}}^{\text{p}}}}{{a + \varepsilon _{\text{d}}^{\text{p}}}}\text{,} $$ (11) 式中,$r_{{\text{dev}}}^{\text{e}}$和a分别为定义弹性核大小和$r_{{\text{dev}}}^{}$变化规律的材料参数,$\varepsilon _{\text{d}}^{\text{p}}$为塑性偏应变。
1.5 塑性乘子
等应力屈服面采用相关联流动法则($ {f_{{\text{iso}}}} = {g_{{\text{iso}}}} $),偏应力屈服面则采用非关联流动法则($ {f_{{\text{dev}}}} \ne {g_{{\text{dev}}}} $),等应力屈服机理产生的塑性体积应变增量及偏应力机理产生的塑性应变增量分别为
$$ {\text{d}}\varepsilon _{\text{v}}^{{\text{p, iso}}} = \lambda _{{\text{iso}}}^{\text{p}}\left[ {\frac{{\partial {g_{{\text{iso}}}}}}{{\partial p'}}} \right]\text{,} $$ (12) $$ \text{d}{\epsilon }_{ij}^{\text{p, dev}}={\lambda }_{\text{dev}}^{\text{p}}\left[\frac{\partial {g}_{\text{dev}}}{\partial {\sigma }_{ij}}\right]={\lambda }_{\text{dev}}^{\text{p}}\frac{1}{M{p}^{\prime }}[\frac{\partial q}{\partial {\sigma }_{ij}}+\alpha \left(M-\frac{q}{{p}^{\prime }}\right)\frac{1}{3}{\delta }_{ij}]。 $$ (13) 其中,
$$ \frac{{\partial q}}{{\partial {\sigma _{ij}}}} = \left\{ \begin{array}{l} {\frac{3}{{2q}}({{\sigma '}_{ij}} - p')}&{(i = j)} \hfill \\ {\frac{{3{{\sigma '}_{ij}}}}{q}}&{(i \ne j)} \hfill \\ \end{array} \right. 。 $$ (14) 据此可得偏应力机理下的塑性体积应变及偏应变分别为[14]
$$ {\text{d}}\varepsilon _{\text{v}}^{{\text{p, dev}}} = \lambda _{{\text{dev}}}^{\text{p}}\left[ {\frac{{\partial {g_{{\text{dev}}}}}}{{\partial p'}}} \right] = \lambda _{{\text{dev}}}^{\text{p}}\frac{\alpha }{{Mp'}}\left[ {M - \frac{q}{{p'}}} \right]\text{,} $$ (15) $$ {\text{d}}\varepsilon _{\text{d}}^{\text{p}} = \lambda _{{\text{dev}}}^{\text{p}}\left[ {\frac{{\partial {g_{{\text{dev}}}}}}{{\partial q}}} \right] = \lambda _{{\text{dev}}}^{\text{p}}\frac{1}{{Mp'}}。 $$ (16) 式中$ {\text{d}}\varepsilon _{\text{v}}^{{\text{p, dev}}} $为偏应力塑性体积应变;$ \lambda _{{\text{iso}}}^{\text{p}} $和$ \lambda _{{\text{dev}}}^{\text{p}} $分别为等应力屈服面及偏应力屈服面的塑性乘子;$ \alpha $为材料参数。
由式(2)可知,前期固结应力$ {p'_{\text{c}}} $与塑性体积应变$ \varepsilon _{\text{v}}^{\text{p}} $相关,且同时影响着两种屈服面;因此,两种屈服面通过塑性体积应变$ \varepsilon _{\text{v}}^{\text{p}} $耦合。当由于其中一种屈服面改变导致了$ \varepsilon _{\text{v}}^{\text{p}} $增大时,另一个屈服面也会同时改变。因此,$ \lambda _{{\text{iso}}}^{\text{p}} $和$ \lambda _{{\text{dev}}}^{\text{p}} $是相关联的($ \lambda _{}^{\text{p}} > 0 $代表加载过程中应力屈服面产生了塑性应变),当两种机制共同作用时,总塑性体积应变由两种屈服机理产生的塑性体积应变共同构成:
$$ {\text{d}}\varepsilon _{\text{v}}^{\text{p}} = \lambda _{{\text{iso}}}^{\text{p}}\left[ {\frac{{\partial {g_{{\text{iso}}}}}}{{\partial p'}}} \right] + \lambda _{{\text{dev}}}^{\text{P}}\left[ {\frac{{\partial {g_{{\text{dev}}}}}}{{\partial p'}}} \right]。 $$ (17) 由于两种塑性机理互相关联,因此两种相容方程必须同时满足,将普拉格相容条件延伸到多机理过程中[14],模型相容方程可表达为
$$ \left. {\begin{array}{*{20}{c}}\text{d}F=\left[\frac{\partial F}{\partial {\sigma }^{\prime }}\right]\left[D\right]\left\{\text{d}\epsilon \right\}-\left[\overline{H}\right]\left[{\lambda }^{\text{p}}\right]-\left[{H}_{\text{T}}\right]\text{d}T\le 0\text{ }\text{,}\\ \text{ }\left[{\lambda }^{\text{p}}\right]\ge 0\text{ }\text{,}\text{ }\\ \text{ d}F\left[{\lambda }^{\text{p}}\right]\ge 0\text{ }。\end{array}} \right\} $$ (18) 其中,
$$ \left[ {\bar H} \right] = \left[ H \right] + \left[ {\frac{{\partial F}}{{\partial \sigma }}} \right]\left[ D \right]\left[ {\frac{{\partial G}}{{\partial \sigma }}} \right]\text{,} $$ (19) $$ \left[ {{H_{\text{T}}}} \right] = \left[ {\frac{{\partial F}}{{\partial \sigma }}} \right]\left[ D \right]\left[ {{\beta _{\text{T}}}} \right] - \left[ {\frac{{\partial G}}{{\partial T}}} \right]。 $$ (20) 式中$ {\text{d}}\sigma ' $为应力增量;$ \pi $为内部变量;F为屈服函数,G为塑性势能函数;$ [{\lambda ^{\text{p}}}] $为塑性乘子;可通过相容方程进行求解,由式(18)可得塑性乘子的表达式:
$$ {\lambda ^{\text{p}}} = {{\text{[}}\bar H{\text{]}}^{ - 1}}\left\{ {\left[ {\frac{{\partial f}}{{\partial \sigma }}} \right]\left[ D \right]\left\{ {{\text{d}}\varepsilon } \right\} - {\text{[}}{H_{\text{T}}}{\text{]d}}T} \right\}\text{,} $$ (21) $ {\text{[}}H{\text{]}} $为硬化模量矩阵,表达式为
$$ \left. {\begin{array}{*{20}{l}}{H}_{\text{ii}}=-\frac{\partial {f}_{\text{iso}}}{\partial {r}_{\text{iso}}}\frac{\partial {r}_{\text{iso}}}{\partial {\lambda }_{\text{iso}}^{\text{p}}}-\frac{\partial {f}_{\text{iso}}}{\partial {\epsilon }_{\text{v}}^{\text{p}}}\frac{\partial {\epsilon }_{\text{v}}^{\text{p}}}{\partial {\lambda }_{\text{iso}}^{\text{p}}}\text{ }\text{,}\\ {H}_{\text{id}}=-\frac{\partial {f}_{\text{iso}}}{\partial {r}_{\text{dev}}}\frac{\partial {r}_{\text{dev}}}{\partial {\lambda }_{\text{dev}}^{\text{p}}}-\frac{\partial {f}_{\text{iso}}}{\partial {\epsilon }_{\text{v}}^{\text{p}}}\frac{\partial {\epsilon }_{\text{v}}^{\text{p}}}{\partial {\lambda }_{\text{dev}}^{\text{p}}}\text{ }\text{,}\\ {H}_{\text{di}}=-\frac{\partial {f}_{\text{dev}}}{\partial {r}_{\text{iso}}}\frac{\partial {r}_{\text{iso}}}{\partial {\lambda }_{\text{iso}}^{\text{p}}}-\frac{\partial {f}_{\text{dev}}}{\partial {\epsilon }_{\text{v}}^{\text{p}}}\frac{\partial {\epsilon }_{\text{v}}^{\text{p}}}{\partial {\lambda }_{\text{iso}}^{\text{p}}}\text{ }\text{,}\\ {H}_{\text{dd}}=-\frac{\partial {f}_{\mathrm{dev}}}{\partial {r}_{\text{dev}}}\frac{\partial {r}_{\text{dev}}}{\partial {\lambda }_{\text{dev}}^{\text{p}}}-\frac{\partial {f}_{\text{dev}}}{\partial {\epsilon }_{\text{v}}^{\text{p}}}\frac{\partial {\epsilon }_{\text{v}}^{\text{p}}}{\partial {\lambda }_{\text{dev}}^{\text{p}}}\text{ }。\end{array}} \right\} $$ (22) 2. ACMEG-T模型在Abaqus软件的二次开发与验证
2.1 二次开发流程
本文基于Abaqus软件中的UMAT子程序功能对ACMEG-T模型进行二次开发。由于Abaqus传入UMAT子程序中的仅为力学应变增量(弹性温度应变在主程序中自动计算),因此适用于Abaqus的相容方程及塑性乘子分别为
$$ \left. {\begin{array}{*{20}{c}}\text{d}F=\left[\frac{\partial F}{\partial {\sigma }^{\prime }}\right][D]\left\{\text{d}\epsilon \right\}-[\overline{H}][{\lambda }^{\text{p}}]\text{+}\left[\frac{\partial F}{\partial T}\right]\text{d}T\le 0\text{ }\text{,}\text{ }\\ \text{ }[{\lambda }^{\text{p}}]\ge 0;\text{d}F[{\lambda }^{\text{p}}]\ge 0\text{ }。\end{array}} \right\} $$ (23) $$ {\lambda ^{\text{p}}} = {{\text{[}}\bar H{\text{]}}^{ - 1}}\left\{ {\left[ {\frac{{\partial F}}{{\partial \sigma }}} \right]{\text{[}}D{\text{]}}\left\{ {{\text{d}}\varepsilon } \right\} + \left[ {\frac{{\partial F}}{{\partial T}}} \right]{\text{d}}T} \right\}。 $$ (24) 将式(12),(13),(24)代入式(1),可得应力增量及弹塑性矩阵表达式为[14]
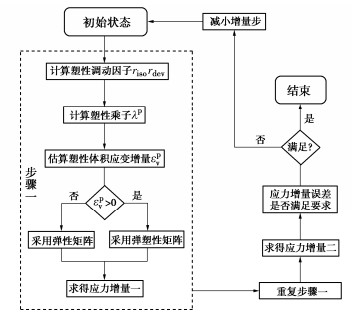
$$ {\text{d}}\sigma = {{\text{[}}D{\text{]}}_{{\text{ep}}}}\left\{ {{\text{d}}\varepsilon } \right\} - {\text{[}}D{\text{]}}\left[ {\frac{{\partial G}}{{\partial \sigma }}} \right]{{\text{[}}\bar H{\text{]}}^{ - 1}}\left[ {\frac{{\partial F}}{{\partial T}}} \right]{\text{d}}T\text{,} $$ (25) $$ {{\text{[}}D{\text{]}}_{{\text{ep}}}} = {\text{[}}D{\text{]}} - {\text{[}}D{\text{]}}\left[ {\frac{{\partial G}}{{\partial \sigma }}} \right]{{\text{[}}\bar H{\text{]}}^{ - 1}}\left[ {\frac{{\partial F}}{{\partial \sigma }}} \right]{\text{[}}D{\text{]}}。 $$ (26) UMAT编写的关键点在于根据传入的应变增量更新应力增量,并给出相应的雅克比矩阵。考虑到应力积分算法的编写难易程度及计算精度,本文采用带误差控制的欧拉算法[20],其中子增量步迭代流程如图 1所示。
2.2 验证与分析
本文分别针对Boom黏土[5]和Bangkok黏土[4]的热力学特性进行对比验证与分析;ACMEG-T热本构模型所对应的土体参数见表 1所示[14, 21]。
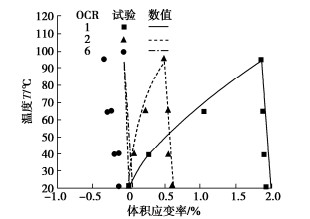
表 1 ACMEG-T热本构模型材料参数表Table 1. Properties of materials used in ACMEG-T thermo-mechanical model模型参数 $ {K_{{\text{ref}}}} $/MPa $ {G_{{\text{ref}}}} $/MPa $ {n^{\text{e}}} $ $ {\beta _{\text{s}}} $/10-5 a b c d $ {\varphi '_0} $/(°) g/10-3 $ \alpha $ $ \beta $ $ r_{{\text{iso}}}^{\text{e}} $ $ r_{{\rm{dev}} }^e $ $ {\gamma _{\text{T}}} $ Boom黏土 130 130 0.4 4 0.007 0.6 0.012 1.3 16 8.5 1 18.00 0.001 0.3 0.20 Bangkok黏土 42 15 1.0 2 0.020 0.2 0.040 1.6 22.66 1.0 2 5.49 0.150 0.1 0.22 不同OCR情况下,Boom黏土体积应变与温度关系曲线如图 2所示。当温度上升时,试样前期固结应力会相应减小,这使得屈服面产生了热软化效应,土体产生了相应的塑性压缩应变;同时,温度上升还会引起土体的热弹性变形。正常固结土在升温过程中产生的塑性压缩变形远大于温度引起的热弹性应变,因此在整个升温过程中表现出较为明显的体积压缩变形。超固结比较大时,升温过程中热软化引起的塑性体积应变较小,热体积应变以弹性膨胀变形为主。本文所采用的ACMEG-T模型中,考虑了不同OCR条件下黏土的应力状态及塑性因子,因此可以很好地反映升温过程中产生的塑性压缩应变值,对试验结果拟合情况良好。
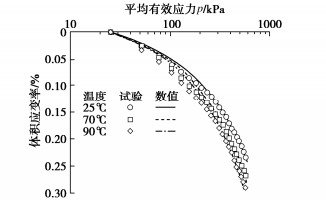
不同温度状态下,正常固结Bangkok黏土在等应力条件下的压缩性状如图 3所示。温度作用下,土体的正常固结线会变动,同时也是由于温度导致了屈服面的收缩,导致应力状态点与屈服面的距离相应减小,塑性因子增大,引起了更大的塑性变形。因此,温度更高的土体在同样的应力增量作用下产生了更大的体积压缩变形。本文所采用的ACMEG-T模型中考虑了屈服极限及塑性因子随体积应变的变化,因此可以很好地反映等向压缩过程中土体力学特性的变化,对试验结果拟合情况良好。
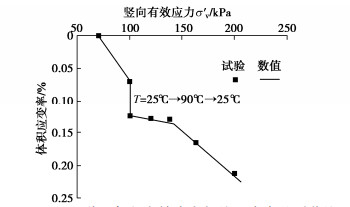
热–力耦合作用下的正常固结Bangkok黏土竖向有效应力与体积应变关系对比曲线如图 4所示。温度循环过程中,土体产生了明显的体积收缩现象,根据式(4),土体的前期固结应力增大,导致随后的100~140 kPa的应力加载阶段,土体呈现出超固结的加载现象,在随后的140~200 kPa加载过程中,重新呈现正常固结土的加载特性。由此可知,在25℃→90℃→25℃的温度循环过程中,土体的前期固结应力上升了约40 kPa;由于ACMEG-T模型考虑了前期固结应力随温度的变化以及塑性因子随加载阶段的变化,因此可以较好地反映热–力耦合作用下土体的体积应变特性,数值模拟结果与试验结果吻合良好。
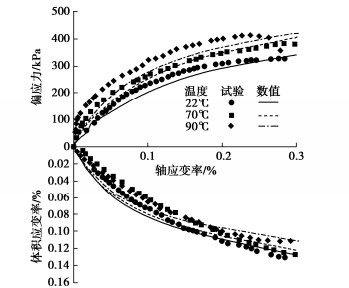
不同温度下正常固结Bangkok黏土轴应变与偏应力及体积应变的关系对比曲线如图 5所示。土体在剪切过程中呈现出剪缩性状,且整体呈现出应变硬化型。这是由于应力状态点在V–lnP平面中位于临界状态线的湿侧,且土体在剪切过程中产生了塑性体积应变,导致了硬化模量的改变。此外,由于土样在升温的过程中,土体产生了一定的体积收缩应变,导致了塑性体积应变的产生,从而使得土体具有更大的前期固结应力。因此,温度较高的土体在剪切过程中会有更大的初始刚度,这与Abuel-Naga等[4]和Cekerevac等[19]的研究结果一致。由于ACMEG-T模型中考虑了硬化模量随塑性因子的变化,因此能够反映剪切过程中的土体变形特性,数值模拟结果与试验实测数据所得规律基本一致。
3. 黏土热–力学特性对能量桩力学特性的影响分析
3.1 研究概况
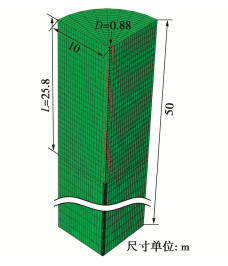
本文基于提出的数值模拟方法,建立了5组热–力耦合3D模型,对不同超固结比条件下(OCR=1,2,4,6,10)黏土地基中能量桩的力学特性进行了研究。全部算例中能量桩的几何模型与Laloui等[22]在洛桑联邦理工学院所开展的现场试验中能量桩的几何一致,其中桩径D为0.88 m,桩长L为25.8 m,数值模型网格图如图 6所示。模型的边界条件为土体底面固定,侧面进行水平约束,顶面自由。
为了研究不同超固结比条件下黏土地基中能量桩–土相互作用机理,全部算例中简化考虑为:桩周土体为Bangkok黏土,土体表面无荷载作用,土体参数见表 1;每轮温度循环的总时长为1 a,其中在夏季工作120 d,冬季工作120 d,桩体温度较环境温度(初始温度25℃)变化量为$ \pm $15℃,两种模式间隔时间为60 d。
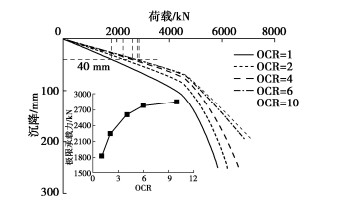
为了确定能量桩顶部机械荷载的大小,除前述建立的5组能量桩热–力耦合3D模型外,本文另外建立了5组模型模拟不同超固结比(OCR=1,2,4,6,10)条件下桩基的静载试验,模型中土体的力学参数与热力耦合3D模型中的参数一致。桩顶荷载–位移关系曲线如图 7所示。由图 7可见,根据《建筑桩基技术规范:JGJ 94—2018》[23]推荐的方法(取40 mm沉降对应的承载力为极限承载力),本文算例中单桩的极限承载力Pu分别为1823,2249,2613,2796,2857 kN。本文5组能量桩热–力耦合数值模型中,首先对能量桩施加工作荷载,荷载大小等于其极限承载力Pu除以安全系数2,随后施加温度循环荷载。
3.2 结果分析与讨论
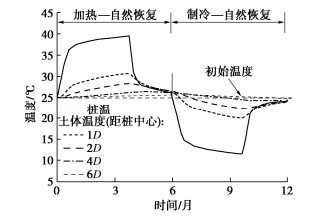
桩体及土体的温度变化如图 8所示。土体温度随桩体温度变化而变化,在距离桩中心1倍桩径处,土体温度的最大变化量为5℃,且随着测点与能量桩轴线距离的增加而逐渐减小。在距离桩中心6倍桩径的位置,土体的温度变化量小于1℃,说明本研究中能量桩的温度影响半径约为6倍桩径。
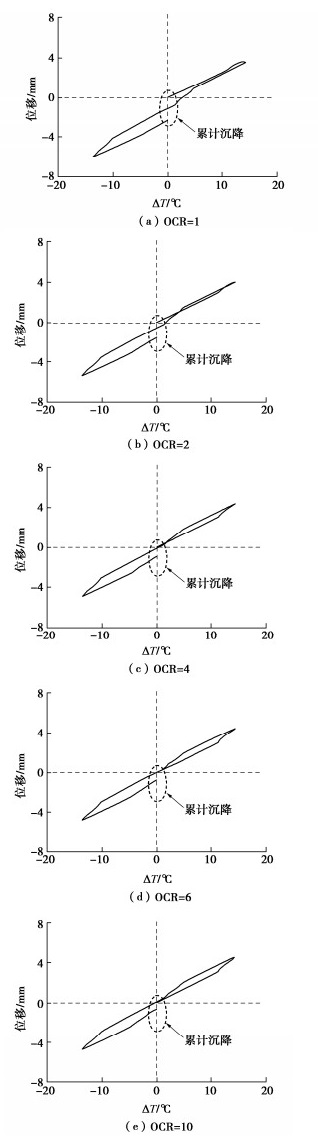
不同超固结比条件下能量桩顶部的位移随桩体温度变化的规律如图 9所示。当桩体温度上升时,桩顶产生向上的位移,随后当桩体温度下降时,能量桩顶部产生沉降。当能量桩经历温度循环过后,尽管桩体温度已恢复至初始状态(桩体温度变化量为0),但桩顶的位移并未恢复至初始状态。这说明温度循环会导致能量桩产生不可恢复的累计沉降。尤其是当土体超固结比(OCR=1)较小时,能量桩经历升温过后,当桩体温度恢复至初始状态时,桩顶产生了明显的累计沉降,约为1.1 mm,在随后的制冷和自然恢复的过程中,能量桩会进一步产生累计沉降,大小约为1.3 mm。
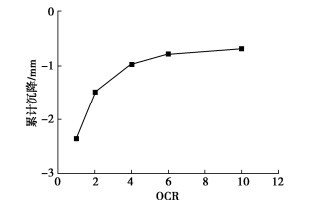
不同超固结比条件下能量桩顶部累计沉降随OCR的变化规律如图 10所示。随着超固结增加,温度循环过后能量桩顶部产生的累计沉降量逐渐减小。当土体的超固结比大于4时,温度循环过后能量桩顶部产生的累计沉降不到1 mm。这一现象可以归因于当土体超固结比较小时,温度升高会导致土体产生明显的体积收缩应变[4-5],即土体升温会导致其产生额外的沉降,从而桩体会受到负摩阻力,导致桩体收到下拉效应,产生额外沉降。但是,当土体的超固结比较大时,温度升高并不会导致土体产生额外的体积收缩应变[4-5],因此能量桩此时不会受到负摩阻力的影响。
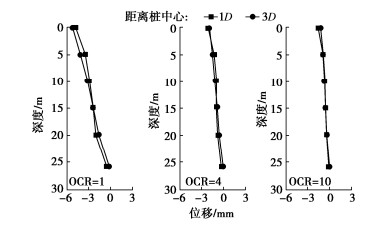
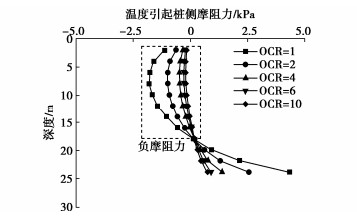
温度循环过后土体的的位移及桩侧摩阻力随深度的变化规律如图 11,12所示。由图 11可知,随着超固结比增加,土体的沉降量逐渐减小,当超固结比大于4时,除了土体表面以外沿深度方向几乎不产生明显的累计量。因此,当超固结比等于1和2时,能量桩上部会产生明显的负摩阻力,最大可达2 kPa,在桩侧负摩阻力的下拉作用下,能量桩产生了额外的累计沉降。而当超固结比大于4时,由于土体此时未产生明显的沉降,因此能量桩受到的负摩阻力较小,导致能量桩产生较小的累计沉降。温度循环过后,能量桩顶部产生的累计沉降最大值(OCR=1时)仅为桩径的0.3%,对桩基承载特性影响不大。
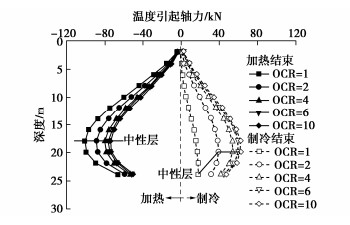
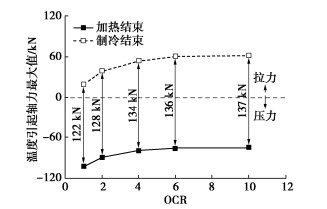
加热阶段和制冷阶段结束时温度荷载引起能量桩产生的额外轴力如图 13所示。尽管制冷和加热过程中能量桩产生的温度变化量相等(见图 8),但加热阶段结束时桩体内产生的额外轴力大于制冷结束时桩体产生的额外轴力。例如,当土体超固结比为10时,加热阶段结束时升温引起桩体产生的最大额外轴力为-75 kN,制冷阶段结束时降温引起桩体产生的最大额外轴力为62 kN。这是由于加热会导致桩体产生径向膨胀,导致桩–土接触压力增大[24],从而导致温度升高过程中土体对桩体轴向热膨胀的约束效应增强。
温度变化引起能量桩产生的额外轴力最大值随土体超固结比的变化如图 14所示。随着土体超固结比逐渐减小,温度荷载引起能量桩轴力呈现出整体逐渐朝压力过渡的规律。例如,相同的桩体温度变化作用下,当土体超固结比为分别为1,2,4,6和10时,加热和制冷结束时桩体产生的最大额外拉(降温)压(升温)轴力的差值分别为轴力变化幅值的69%,39%,19%,12%和9%。这是由于温度变化引起能量桩产生的额外应力为桩侧负摩阻力引起的压应力叠加土体约束引起的温度应力,且随着超固结比减小,负摩阻力引起桩体内产生的压应力逐渐增大,导致能量桩产生的额外轴力整体逐渐向压力过渡。
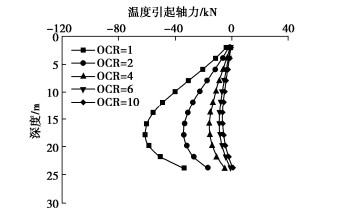
温度循环过后桩体轴力随深度变化如图 15所示。温度循环过后桩土温度基本恢复至初始状态(图 8)。由图 15可知,当土体的超固结比OCR=1时,温度循环过后桩体内累积的轴力大小最大为62 kN。随着超固结比增加,温度循环引起的不可恢复轴力逐渐减小。这是由于随着超固结增加,温度引起的土体沉降逐渐减弱,导致桩侧负摩阻力降低,进而导致桩体收到的下拽作用较小,这与图 10~14中的结果相吻合。另外,温度荷载引起土体产生的累计沉降以及桩侧负摩阻力对能量桩的承载力特性的影响却不容忽视。当土体超固结比OCR=1时,温度循环过后,桩体内产生的最大不可恢复轴力的大小为桩基工作荷载的6.8%。当土体超固结比大于4时,桩体内的最大不可恢复轴力仅为桩基工作荷载的1.2%,基本可忽略不计。
4. 结论
(1)本文将ACMEG-T土体热本构模型在Abaqus软件中进行了二次开发,推导了适用的弹塑性矩阵及塑性乘子并给出了子增量步迭代流程图。利用编写的UMAT子程序对能够反应黏土热–力耦合特性的三轴试验结果进行模拟与分析,验证了其准确性和可靠性。
(2)基于建立的热–力耦合数值模型,分析了黏土的热–力学特性对能量桩力学特性的影响规律。正常固结黏土中,当土体受到温度荷载过后会产生累计沉降,导致桩侧产生额外的负摩阻力,进而导致能量桩会产生不可恢复的沉降和轴力。
(3)随着土体超固结比逐渐增加,土体的热–力学特性对能量桩位移特性和轴向力学响应的影响逐渐减弱。温度荷载作用下,土体累计沉降所引起的能量桩累计沉降最大值(OCR=1时)仅为桩径的0.3%,可忽略不计。但是当OCR较小时,土体累计沉降引起的桩体不可恢复轴力却不可忽略(最大为桩基工作荷载的6.8%),仅当土体的超固结比大于4时,这一影响才可忽略不计。
-
表 1 ACMEG-T热本构模型材料参数表
Table 1 Properties of materials used in ACMEG-T thermo-mechanical model
模型参数 Kref/MPa Gref/MPa ne βs/10-5 a b c d φ′0/(°) g/10-3 α β reiso redev γT Boom黏土 130 130 0.4 4 0.007 0.6 0.012 1.3 16 8.5 1 18.00 0.001 0.3 0.20 Bangkok黏土 42 15 1.0 2 0.020 0.2 0.040 1.6 22.66 1.0 2 5.49 0.150 0.1 0.22 -
[1] BRANDL H. Energy foundations and other thermo-active ground structures[J]. Géotechnique, 2006, 56(2): 81–122. doi: 10.1680/geot.2006.56.2.81
[2] 刘汉龙, 孔纲强, 吴宏伟. 能量桩工程应用研究进展及PCC能量桩技术开发[J]. 岩土工程学报, 2014, 36(1): 176–181. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201401024.htm LIU Han-long, KONG Gang-qiang, NG C. Review of the applications of energy pile and technical development of PCC energy pile[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 176–181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201401024.htm
[3] 桩基地热能利用技术标准: JGJ/T 438—2018[S]. 2018. Technical Stanard for Utlization of Geothermal Energy through Piles: JGJ/T 438—2018[S]. 2018. (in Chinese)
[4] ABUEL-NAGA H M, BERGADO D T, RAMANA G V, et al. Experimental evaluation of engineering behavior of soft Bangkok clay under elevated temperature[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(7): 902–910. doi: 10.1061/(ASCE)1090-0241(2006)132:7(902)
[5] BALDI G, HUECKEL T, PEANO A. Developments in Modeling of Thermo-Hydro-Mechanical Behavior of Boom Clay and Clay-Based Buffer Materials[R]. Luxembourg: Commission of the European Communities, 1991.
[6] HUECKEL T, BORSETTO M. Thermoplasticity of saturated soils and shales: constitutive equations[J]. Journal of Geotechnical Engineering, 1990, 116(12): 1765–1777. doi: 10.1061/(ASCE)0733-9410(1990)116:12(1765)
[7] CUI Y J, SULTAN N, DELAGE P. A thermomechanical model for saturated clays[J]. Canadian Geotechnical Journal, 2000, 37(3): 607–620. doi: 10.1139/t99-111
[8] 姚仰平, 李自强, 侯伟, 等. 基于改进伏斯列夫线的超固结土本构模型[J]. 水利学报, 2008, 39(11): 1244–1250. doi: 10.3321/j.issn:0559-9350.2008.11.013 YAO Yang-ping, LI Zi-qiang, HOU Wei, et al. Constitutive model of over-consolidated clay based on improved Hvorslev envelope[J]. Journal of Hydraulic Engineering, 2008, 39(11): 1244–1250. (in Chinese) doi: 10.3321/j.issn:0559-9350.2008.11.013
[9] 姚仰平, 杨一帆, 牛雷. 考虑温度影响的UH模型[J]. 中国科学(技术科学), 2011, 41(2): 158–169. https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201102004.htm YAO Yang-ping, YANG Yi-fan, NIU Lei. UH model considering temperature effects[J]. Scientia Sinica (Technologica), 2011, 41(2): 158–169. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JEXK201102004.htm
[10] ZHOU C, NG C W W. A thermomechanical model for saturated soil at small and large strains[J]. Canadian Geotechnical Journal, 2015, 52(8): 1101–1110. doi: 10.1139/cgj-2014-0229
[11] 程晓辉, 陈志辉. 纯主应力旋转条件下饱和黏土累积变形的热力学模型分析[J]. 岩土工程学报, 2015, 37(9): 1581–1590. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509006.htm CHENG Xiao-hui, CHEN Zhi-hui. Thermodynamic modeling of accumulated deformation of saturated clays under pure principal stress rotation[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1581–1590. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509006.htm
[12] 陈志辉, 程晓辉. 饱和土体固结压缩和蠕变的热力学本构理论及模型分析[J]. 岩土工程学报, 2014, 36(3): 89–498. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403016.htm CHEN Zhi-hui, CHENG Xiao-hui. Thermodynamic constitutive theory and analysis of consolidation compression and creep of saturated soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 89–498. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201403016.htm
[13] LALOUI L, CEKEREVAC C. Thermo-plasticity of clays: an isotropic yield mechanism[J]. Computers and Geotechnics, 2003, 30(8): 649–660. doi: 10.1016/j.compgeo.2003.09.001
[14] LALOUI L, FRANÇOIS B. ACMEG-T: soil thermoplasticity model[J]. Journal of Engineering Mechanics, 2009, 135(9): 932–944. doi: 10.1061/(ASCE)EM.1943-7889.0000011
[15] 费康, 钱健, 洪伟, 等. 黏土地基中能量桩力学特性数值分析[J]. 岩土力学, 2018, 39(7): 2651–2661. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201807040.htm FEI Kang, QIAN Jian, HONG Wei, et al. Numerical analysis of mechanical behavior of energy piles in clay[J]. Rock and Soil Mechanics, 2018, 39(7): 2651–2661. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201807040.htm
[16] 姚仰平, 冯兴, 黄祥, 等. UH模型在有限元分析中的应用[J]. 岩土力学, 2010, 31(1): 237–245. doi: 10.3969/j.issn.1000-7598.2010.01.041 YAO Yang-ping, FENG Xing, HUANG Xiang, et al. Application of UH model to finite element analysis[J]. Rock and Soil Mechanics, 2010, 31(1): 237–245. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.01.041
[17] DI DONNA A, LALOUI L. Numerical analysis of the geotechnical behaviour of energy piles[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(8): 861–888. doi: 10.1002/nag.2341
[18] HONG P Y, PEREIRA J M, TANG A M, et al. On some advanced thermo-mechanical models for saturated clays[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(17): 2952–2971
[19] CEKEREVAC C, LALOUI L. Experimental study of thermal effects on the mechanical behaviour of a clay[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2004, 28(3): 209–228.
[20] POTTS D M, ZDRAVKOVIĆ L. Finite Element Analysis in Geotechnical Engineering: Application[M]. London: Thomas Telford, 2001.
[21] LALOUI L, CEKEREVAC C. Numerical simulation of the non-isothermal mechanical behaviour of soils[J]. Computers and Geotechnics, 2008, 35(5): 729–745.
[22] LALOUI L, NUTH M, VULLIET L. Experimental and numerical investigations of the behaviour of a heat exchanger pile[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(8): 763–781.
[23] 建筑桩基技术规范: JGJ 94—2008[S]. 2008. Technical Code for Building Pile Foundations: JGJ 94—2008[S]. 2008. (in Chinese)
[24] LUO J, ZHANG Q, ZHAO H F, et al. Thermal and thermomechanical performance of energy piles with double U-loop and spiral loop heat exchangers[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(12): 04019109.
-
期刊类型引用(5)
1. 赵华,王成龙,陈志雄,张鼎新,彭宸. 饱和黏土中水平受荷能量桩热–力响应特性研究. 岩石力学与工程学报. 2024(01): 248-260 .  百度学术
百度学术
2. 曹卫平,李清源,赵敏,吴奇兴,李庆. 间歇式运行模式下黄土地基中能量桩热-力特性模型试验. 土木工程学报. 2024(09): 123-134 .  百度学术
百度学术
3. 徐云山,肖子龙,孙德安,陈军浩,曾召田. 土体导热系数温度效应及其预测模型. 岩土工程学报. 2023(06): 1180-1189 .  本站查看
本站查看
4. 宫玉辉,陈向南,刘鸣,米洋,张鹏,朱珍. “双碳”背景下能量桩在工程建设领域的研究与应用. 建设科技. 2023(10): 61-66 .  百度学术
百度学术
5. 晁军. 不同运行桩数下能量桩群桩承台变形规律研究. 河南科学. 2022(06): 956-963 .  百度学术
百度学术
其他类型引用(11)



 下载:
下载: