光滑粒子流体动力学方法在饱和边坡地震滑移大变形中的适用性研究

黄帅; 刘传正; GODAKatsuichiro

doi:10.11779/CJGE20211274

光滑粒子流体动力学方法在饱和边坡地震滑移大变形中的适用性研究 English Version

1.
应急管理部国家自然灾害防治研究院, 北京 100085
2.
韦仕敦大学, 伦敦 N6A3K7, 加拿大

基金项目:

国家自然科学基金项目 51708516

博士后基金项目 2021M691391

地震数值预测联合实验室开放基金项目 2021LNEF04

详细信息

作者简介:
作者简介：黄帅(1987—)，男，博士，副研究员，主要从事工程防震减灾研究。E-mail: shuaihuang@ninhm.ac.cn

中图分类号: TU435
计量
- 文章访问数: 296
- HTML全文浏览量: 75
- PDF下载量: 120
出版历程
- 收稿日期: 2021-12-06
- 网络出版日期: 2023-02-23
- 刊出日期: 2023-01-31

Applicability of smooth particle hydrodynamics method to large sliding deformation of saturated slopes under earthquake action

1.
National Institute of Natural Hazards, MEMC, Beijing 100085, China
2.
Western University, London N6A 3K7, Canada

摘要

摘要: 地震作用下饱和边坡破坏会产生滑移大变形行为，一般难以采用有限元等网格方法进行分析，而光滑粒子流体动力学方法可以轻松处理大变形问题。基于此，通过在光滑粒子流体动力学方法（SPH方法）中加入瑞利衰减阻尼，基于有效应力本构模型改进了SPH方法的运动方程，建立了用于饱和边坡地震滑移大变形的数值计算方法；之后与饱和土样的空心圆柱扭剪试验获取的有效应力路径和剪应力-应变滞回曲线进行了对比，取得了较为一致的结果，验证了本改进方法的可行性。最后采用建立的数值计算方法，分析了不同SPH粒子密度下饱和边坡的地震滑移行为并与Newmark方法进行了对比。研究发现，改进的SPH方法确定的饱和边坡地震滑移临界面形状与Newmark方法对数螺旋滑移面形状吻合较好；因此改进的SPH方法能较好的再现饱和边坡地震作用下的滑移大变形过程，但该方法中边坡地震滑移大变形分析结果受设置的粒子密度影响。
- 地震作用 /
- 滑移大变形 /
- 光滑粒子流体动力学方法 /
- Newmark方法 /
- 临界滑移面
Abstract: The failure of a saturated slope under an intense earthquake ground motion will produce large sliding deformation, which is difficult to analyze using the finite element method. However, the smooth particle hydrodynamics method (SPH method) can deal with large deformation easily. In this study, to develop a new numerical method for calculating the seismic sliding large deformation of saturated slopes, the motion equation for the SPH method is improved by (1) introducing the Rayleigh damping into the smooth particle hydrodynamics and (2) adopting the effective stress constitutive model. To evaluate the effectiveness of the new method at soil element levels, the effective stress path and shear stress-strain hysteresis curve are obtained through the hollow cylindrical torsional shear tests on saturated soil samples, and are compared with the simulated results. The consistent results are obtained to verify the feasibility of the improved method. Finally, the seismic sliding behavior of saturated slopes under different SPH particle densities is analyzed by using the established numerical method and compared with that by the Newmark's sliding block method. It is found that the key parameter of the improved method is the particle density and that the shape of seismic sliding critical surface of saturated slopes determined by the improved SPH method is in good agreement with that of logarithmic spiral slip surface determined by the Newmark's method. Therefore, the improved SPH method can also be used to simulate a large sliding deformation process of saturated slopes under seismic actions.
- earthquake action /
- large sliding deformation /
- smooth particle hydrodynamics method /
- Newmark method /
- critical slip surface

HTML全文

0. 引言

自然界中存在着大量的饱和边坡，例如强降雨引起堰塞坝、冰湖冰碛坝暂态性饱和以及水底边坡等，此类边坡不同于一般的无水边坡，当地震发生时，饱和边坡在地震和地下水共同作用下会产生超静孔隙水压力从而导致边坡发生滑塌。例如，2003年7月日本宫城县地震中，大量岸坡出现严重损坏，震前强降雨导致边坡内部接近饱和，使得岸顶部出现了约3 m左右的高低差，坡脚出现了3~5 m的堆积体。由此可知，饱和边坡内由于含水率高，加之地震诱发的超静孔隙水压力作用，在地震作用下更容易发生滑塌破坏，确定饱和边坡地震稳定性分析的简易评价方法，从而采取有效的防治措施，对于阻止灾害发生具有重要意义。

目前，有限元方法是边坡地震滑移变形分析中常用的数值分析方法^[1-2]。然而，由于在有限元法中需要使用网格划分方法，当目标变形较大时，存在网格扭曲且精度大幅降低，或难以继续进行分析的问题。因此，有限元方法在预测滑移大变形方面还存在不足。例如，黄帅等^[3]基于砂质边坡的弹塑性有限元模型研究了地下水对边坡地震动力响应的影响规律，但是没有给出边坡的滑移形式；董士杰等^[4]在不考虑地下水影响时，给出了地震作用下加筋土边坡变塑性分布情况，但是其不能反映边坡的大变形过程；同样，王飞等^[5]和Yin等^[6]研究了地震作用下边坡的变形和破坏特征，但是均只能给出边坡的最大剪应变和变形的云图，没能实现边坡滑移大变形模拟。而光滑粒子流体动力学方法（SPH）采用拉格朗日坐标系的运动方程进行计算，不需要创建网格，因此它具有适用于大变形问题的优点。近年来，SPH在弹塑性体大变形分析方面取得了一定进展，已被应用于岩土工程领域^[9]，例如唐宇峰等^[10]研究发现SPH计算的边坡安全系数与极限平衡法及有限元法十分接近，均可作为失稳判据。Nonoyama等^[11]进一步推动了SPH方法在边坡稳定性分析中的应用。Zhang等^[12]提出了一种基于SPH的黏性土边坡滑坡模拟方法，并与有限元方法进行对比，其模拟效果吻合较好。张卫杰等^[13]基于Biot固结原理提出了一种基于正则化修正的水土耦合SPH数值模型，并将该模型用于模拟三维水体溃坝模拟，但是该改进模型采用弹性模型描述土骨架的应力-应变关系，并不涉及外部动力荷载。另外，还有研究者采用SPH方法，提出了适用于土体大变形流滑分析的三维SPH仿真模型，并应用于土体流滑特性的模拟^[14-16]。因此，由于SPH方法具有大变形分析的优点，已被国内外学者应用在了边坡的大变形分析中，并验证了其可行性；然而对于地震作用下边坡的临界滑移面形状及其大变形特性分析，尤其是含有地下水的边坡在地震作用下会产生超静孔隙水压力，如何在SPH方法中进行考虑，需要进一步深入研究。

综上，本研究通过在SPH方法的地震响应分析中引入了有效应力的本构模型和瑞利衰减，建立了基于改进SPH方法的边坡地震滑移大变形的数值模型。之后，进行了饱和边坡地震滑移行为的再现分析，并研究了改进的SPH方法中粒子密度对饱和边坡地震滑移面和破坏模式的影响规律，最后将本文提出的数值模型与Newmark方法进行了对比分析。

1. 基于改进SPH方法的数值模型建立

1.1 SPH基本理论方法

SPH方法中核近似是通过以下公式进行计算^[17]：

$f(x) = \int {f(x')} W(|x - x'|,h){\text{d}}x' \text{，}$

(1)

式中，W为权函数， $x - x'$ 为粒子之间距离，h为平滑距离。核函数要求在整个区域中积分的值为1以及h→0的极限为狄拉克δ函数。而且在式（1）中，权函数W被狄拉克δ函数代替的那个数值是关于δ函数之和相关的恒等式，核近似可以解释为近似核等式。

将式（1）的积分式通过粒子近似的方法进行离散化：

$f({x^i}) = \sum\limits_{j = 1}^N {\frac{{{m^j}}}{{{\rho ^j}}}f({x^j})W(|{x^j} - {x^i}|,h)} \text{，}$

(2)

式中，xⁱ为SPH粒子坐标，N为距离粒子i的距离内存在的粒子数。虽然SPH粒子在它们的坐标值xⁱ处有质量mⁱ，密度ρⁱ，体积 ${m^j}/{\rho ^j}$ ，函数值 $f({x^i})$ ，但没有明确的形状。即，SPH方法中的粒子是与有限元法中的高斯点和节点相当的概念，而且与离散单元法中的粒子完全不同。通常，在对连续介质进行分析时，除了函数 $f(x)$ ，还要对其微分形式 $\nabla \cdot f(x)$ 进行评价^[18]。根据式（2）可以得到

$\nabla \cdot f(x) = \int {\nabla \cdot f(x')W(x - x',h){\text{d}}x'} 。$

(3)

此时，

$\nabla \cdot f(x')W(x - x',h) = \nabla \cdot \{ f(x')W(x - x',h)\} -\\ \;\;\;\;\;\;\;\;\;\;\;\;\int {f(x') \cdot \nabla W(x - x',h)} 。$

(4)

所以可以将式（3）转化为

$\nabla \cdot f(x) = \int {\nabla \cdot \{ f(x')W(x - x',h)\} } {\text{d}}x' - \\ \;\;\;\;\;\;\;\;\;\;\;\; \int {f(x') \cdot \nabla W(x - x',h){\text{d}}x'} 。$

(5)

根据散度定理，可得

$\int {\nabla \cdot \{ f(x')W(x - x',h)\} } {\text{d}}x' \\ \;\;\;\;\;\;\;\; = \int_s {f(x')W(x - x',h) \cdot \widehat n{\text{d}}S} = 0 。$

(6)

因此，函数 $f(x)$ 微分形式 $\nabla \cdot f(x)$ 内核近似为

$< \nabla \cdot f(x) > = - \int {f(x') \cdot \nabla W(x - x',h){\text{d}}x'} 。$

(7)

利用粒子将式（7）离散化，可得到

$< \nabla \cdot f(x) > = - \sum\limits_{k = 1}^N {\frac{{f({x_k})}}{{\rho ({x_k})}} \cdot \nabla W(x - {x_k},h){m_k}} 。$

(8)

针对W函数目前已经提出了很多形式，本文采用比较成熟的三次样条函数^[12]。内核函数 $W(x - {x_k},h)$ 满足

$\mathop {\lim }\limits_{h \to 0} W(x - x',h) = \delta (x - x') \text{，}$

(9)

$\int {W(x,h){\text{d}}x = 1} 。$

(10)

在计算平滑距离h内的点的物理量 $f({x^i})$ 时，该粒子平滑距离h内的粒子的值的加权平均作为核函数的值，相当于求出一个权重；超出h的粒子，核函数值为零，不计入计算^[19]。对于平滑距离h计算精度会随着h的值而变化问题，岩本哲也等^[20]应用Chen等^[21]提出的Corrective Smoothed Particle Method（CSPM）方法，可以大幅提高分析精度对h的依赖性。因此，在本研究中也将采用CSPM方法代替原始SPH方法的公式化进行计算。在CSPM方法中， $f({x^i})$ 及其微分形式为

$f({x^i}) = \frac{{\sum\limits_{j = 1}^N {\frac{{{m^j}}}{{{\rho ^j}}}f({x^j}){W^{ij}}} }}{{\sum\limits_{j = 1}^N {\frac{{{m^j}}}{{{\rho ^j}}}{W^{ij}}} }} \text{，}$

(11)

$\frac{{\partial f({x^i})}}{{\partial {x_\alpha }}} \cdot \sum\limits_{j = 1}^N {\frac{{{m^j}}}{{{\rho ^j}}}(x_\alpha ^j - x_\alpha ^i)\frac{{\partial {W^{ij}}}}{{\partial {x_\beta }}}} \\ \;\;\;\;\;\;\;\;\; = \sum\limits_{j = 1}^N {\frac{{{m^j}}}{{{\rho ^j}}}\{ f({x^j}) - f({x^i})\} \frac{{\partial {W^{ij}}}}{{\partial {x_\beta }}}} 。$

(12)

岩土体等弹性体或弹塑性体的运动方程为

$\ddot u(z) = \frac{1}{{\rho (z)}}\frac{{{\text{d}}\tau (z)}}{{{\text{d}}z}} \text{，}$

(13)

式中， $\ddot u(z)$ 为深度z上水平方向加速度， $\tau (z)$ 为简剪切应力， $\rho (z)$ 为密度。如果是弹性体，可以用剪切刚性G与剪切应变 $\gamma (z)$ 以来表示剪切应力 $\tau (z)$ ：

$\tau (z) = G\gamma (z) \text{，}$

(14)

或者用增量的形式来表示：

${\text{d}}\tau (z) = {G_0}{\text{d}}\gamma (z) 。$

(15)

另外，剪切应变 $\gamma (z)$ 可以表示为

$\gamma (z) = \frac{{{\text{d}}u(z)}}{{{\text{d}}z}} 。$

(16)

本文中，笔者采用SHP方法针对式（13）近似求解。首先，通过内核近似^[22]来求 ${\text{d}}u(z){\text{/d}}t$ 。此时，考虑到通常存在的数值稳定性问题，不把 $u(z)$ 直接代入式（13），而是根据

$\nabla \cdot f(x) = \frac{1}{\rho }[\nabla \cdot \{ \rho f(x)\} - f(x) \cdot \nabla \rho ]$

(17)

进行改写的部分运用内核近似。

关于粒子a的剪切应变利用式（18）求解：

${\gamma _{\text{a}}} = \frac{{{\text{d}}{u_{\text{a}}}}}{{{\text{d}}z}} = \sum\limits_{\text{b}}^{} {\frac{{{m_{\text{b}}}}}{{{\rho _{\text{b}}}}}({u_{\text{a}}} - {u_{\text{b}}})\frac{{{\text{d}}{W_{{\text{ab}}}}}}{{{\text{d}}z}}} \text{，}$

(18)

式中，下标a，b分别为求物理量的粒子与包含于其影响半径内的粒子。另外，其核函数满足

${W_{{\text{ab}}}} = W({x_{\text{a}}} - {x_{\text{b}}},h) 。$

(19)

因此，由式（18）求得的剪切应变 ${\gamma _{\text{a}}}$ ，通过式（14）来求剪切应力 ${\tau _{\text{a}}}$ 。

接下来，针对式（13）运用恒等式（20）求边坡不同深度的加速度：

$\nabla \cdot f(x) = \rho \left( {\nabla \cdot \frac{{f(x)}}{\rho } + \frac{{f(x)}}{2} \cdot \nabla \rho } \right) \text{，}$

(20)

$\ddot u(z) = \sum\limits_{\text{b}}^{} {{m_{\text{b}}}\left( {\frac{{{\tau _{\text{a}}}}}{{\rho _{\text{a}}^2}} + \frac{{{\tau _{\text{b}}}}}{{\rho _{\text{b}}^2}}} \right)} \frac{{{\text{d}}{W_{{\text{ab}}}}}}{{{\text{d}}z}} 。$

(21)

在求得粒子a的加速度后，根据得到的 ${\ddot u_{\text{a}}}$ 来求粒子a的移动量，更新密度 ${\rho _{\text{a}}}$ ：

${\rho _{\text{a}}} = \sum\limits_{\text{b}}^{} {{m_{\text{b}}}{W_{ab}}} 。$

(22)

如果对于非饱和边坡在地震作用下需要考虑超静孔隙水压力的作用，因此需要采用有效应力分析，土的应力-应变关系属于非线性模型，则可以通过将式（14）或式（15）转换为有效应力模型，然后运用SPH方法对边坡模型进行分析。

1.2 SPH方法改进

为了能模拟地震作用下饱和边坡的动力行为，采用有效应力法进行加速度的求解。对于松散砂土循环剪切试验时，超静孔隙水压力随着剪切力的增加而单调增加；而密砂情况下，砂土在达到一定的剪应力比时变得松散，此时，超静孔隙水压力像松散砂土一样随循环剪切力而单调增加；但当剪应力比超过某一应力比时，因剪切而产生的正的剪胀性会导致超静孔隙水压力减小。该应力比一般被称为相变角，在循环剪切过程中，数值一定。如果是紧密砂土，在达到相变角后，随着剪切应力比的增加，由于剪胀效应，孔隙水压力会减小，但如果不超过一定数值，当剪切应力比大到一定程度后，水压力不变。在此项研究中，有效应力的本构模型，采用了社本模型^[23]。

有效应力模型的应力-应变关系采用Ramberg- Osgood模型^[24]，其可用于非线性分析的三参数模型。在大变形过程中，有效应力会随着循环剪切的进行而发生变化。因此，应力-应变关系可以用增量形式表示为

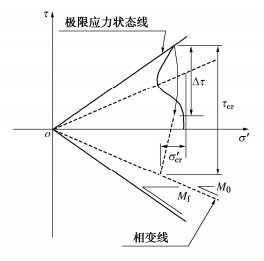
${\text{d}}\gamma = \frac{{{\text{d}}\tau }}{{{G_0}}}\left( {1 + \alpha \beta |\frac{{\Delta \tau }}{{{{G'}_0}}}{|^{\beta - 1}}} \right) 。$

(23)

式中： $\gamma$ 为剪切应变； $\tau$ 为剪切应力； $\Delta \tau$ 为剪切应力卸载时的平均剪切应力增量（参见）。该关系由增量显示表示，如式（24），（25）所示。 $\alpha$ 和 $\beta$ 分别表示由方程（24）给出， ${G_0}$ 是由方程（25）计算的初始剪切弹性系数。另外， ${G_0}_i$ 在骨架曲线上的值为 ${G_0}$ ，在滞回曲线上的值为2 ${G_0}$ 。

$\alpha = {\left( {\frac{2}{{{\gamma _{{\text{rf}}}}}}} \right)^{\beta - 1}} \text{，} \beta = \frac{{2 + {\text{π }}{h_{\max }}}}{{2 - {\text{π }}{h_{\max }}}} \text{，}$

(24)

${G_0} = {G_{0i}}{\left( {\frac{{{{\sigma '}_{\text{m}}}}}{{{{\sigma '}_{{\text{mi}}}}}}} \right)^m} \text{，} {\gamma _{{\text{rf}}}} = {\gamma _{{\text{rfi}}}}{\left( {\frac{{{{\sigma '}_{\text{m}}}}}{{{{\sigma '}_{{\text{mi}}}}}}} \right)^{mr}} 。$

(25)

图 1 有效应力路径

Figure 1. Effective stress path

下载: 全尺寸图片幻灯片

式中： ${\sigma '_{\text{m}}}$ 为有效围压， ${\sigma '_{{\text{mi}}}}$ 为初始有效围压； ${\gamma _{{\text{rf}}}}$ 为 ${\sigma '_{\text{m}}}$ 中的标准应变；h_max为最大衰减常数，m， ${m_{\text{r}}}$ 为初期剪切刚度及标准剪切应变围压依赖性的常数，可取0.5。

对于社本模型，在发生循环剪切现象的阶段，超静孔隙水压力上升程度的变化以及循环剪切的进行，要小于以往的试验结果，所以本文采用初始有效围压 ${\sigma '_{{\text{mi}}}}$ 替有效围压 ${\sigma '_{\text{m}}}$ 。

在大变形分析中，目标物体中发生的旋转有时是不能忽略的。由于简单地将柯西应力对时间微分得到的应力速度不具有客观性，因此存在应力值因坐标轴的旋转而明显变化的问题。Gray等^[25]引入Jaumann应力速度来消除这种明显的应力变化：

${\hat \sigma _{\alpha \beta }} = {\dot \sigma _{_{\alpha \beta }}} - {\omega _{\alpha \gamma }}{\sigma _{\gamma \beta }} + {\sigma _{\alpha \gamma }}{\omega _{\gamma \beta }} \text{，}$

(26)

式中， ${\hat \sigma _{\alpha \beta }}$ 为Cauchy应力增量， ${\omega _{\alpha \beta }}$ 为一个自旋张量，

${\omega _{\alpha \beta }} = \frac{1}{2}\left( {\frac{{\partial {\nu _\alpha }}}{{\partial {x_\beta }}} - \frac{{\partial {\nu _\beta }}}{{\partial {x_\alpha }}}} \right) 。$

(27)

由于岩土体结构存在阻尼，因此地震波传播过程中会存在衰减行为，在地震工程学领域广泛使用的有限元法的地震响应分析中，大部分情况下使用瑞利衰减。在有限元法中，瑞利衰减矩阵[C]使用 ${\alpha _{\text{R}}}$ 和 ${\beta _{\text{R}}}$ 表示为

$\left[ C \right] = {\alpha _{\text{R}}}\left[ M \right] + {\beta _{\text{R}}}\left[ K \right] 。$

(28)

式中：[M]为质量矩阵；[K]为刚度矩阵。在有限元法中，质量矩阵中有匹配质量矩阵和集中质量矩阵，当分析对象的物体具有材料非线性时，式（28）中的刚度矩阵[K]对应于切线刚度矩阵。在集中质量矩阵中，矩阵的对角分量为正值，所有非对角分量均为零。因为对角分量的值是分配给相应节点的质量，所以在SPH方法中可以认为是对应粒子的质量。

在有限元方法中，式（28）的衰减矩阵作用于节点速度矢量。即，当时间t处的节点速度矢量为 $\left\{ {{v_t}} \right\}$ 时，由瑞利衰减引起的衰减力矢量为

$\left[ C \right]\left\{ {{v_t}} \right\} = {\alpha _R}\left[ M \right]\left\{ {{v_t}} \right\} + {\beta _R}\left[ K \right]\left\{ {{v_t}} \right\} 。$

(29)

式（39）的右边第二项满足

$\left[ K \right]\left\{ {{v_t}} \right\} \approx \left[ K \right]\frac{{\left\{ {{u_t}} \right\} - \left\{ {{u_{t - \Delta t}}} \right\}}}{{\Delta t}}\\ \;\;\;\;\;\;\;\; = \frac{{\left\{ {{f_t}} \right\} - \left\{ {{f_{t - \Delta t}}} \right\}}}{{\Delta t}} 。$

(30)

式中：{u_t}，{f_t}分别表示时刻t处的节点位移矢量、恢复力矢量；Δt为时间增量。由此，式（29）的右边第二项可以解释为在从要素的应力状态得到的节点力的时间增量乘以系数β。

综上，为了在SPH方法中引入瑞利衰减，在式（13）运动方程的右边增加衰减项：

$\ddot u(z) = \frac{1}{{\rho (z)}}\frac{{{\text{d}}\tau (z)}}{{{\text{d}}z}}{\text{ + }}{\alpha _R}{\nu _\alpha } + {\beta _R}\frac{{\Delta {g_\alpha }}}{{\Delta t}} 。$

(31)

在SPH方法中，每个时间步长通过运动方程（31）求出粒子的加速度，并更新速度和粒子坐标。在时间 $t$ 中，当粒子的加速度为 $\ddot u{\text{(}}z,t{\text{)}}$ ，速度用 $\dot u(z,t)$ 表示，位移用 $u(z,t)$ 表示时，下一个时间步长 $t + \Delta t$ 中的粒子速度 $\dot u(z,t + \Delta t)$ 、粒子位置 $u(z,t + \Delta t)$ 可以通过下式得到^[26]：

$\dot u(z,t + \vartriangle t) = \dot u(z,t) + \ddot u(z,t + \vartriangle t) \cdot \vartriangle t \text{，}$

(32)

$u(z,t + \Delta t) = u(z,t) + \dot u(z,t + \Delta t) \cdot \Delta t 。$

(33)

综上，在光滑粒子流体动力学方法（SPH方法）中加入瑞利衰减阻尼，基于有效应力本构模型改进SPH方法的运动方程，然后基于改进的开源代码程序即可实现地震作用下饱和边坡的大变形模拟。SPH方法的计算流程图如图 2所示。

图 2 SPH方法的计算流程图

Figure 2. Flow chart of SPH method

下载: 全尺寸图片幻灯片

由图 2可知，基于SPH方法的计算在初始运行阶段会从输入文件中读入包含有粒子类型、坐标、速度、半径、密度、体积和压强等物理属性信息。随后系统进入时间步长积分的主循环阶段，时间步数istep从0开始每循环一次增加1，每当系统完成一次循环后，会判断是否满足可视化条件或输出条件，如果满足则系统将绘制出计算结果的粒子分布图和等值线图，如果满足输出条件则系统将输出并储存该时刻的相关数据信息。最后系统将判断是否满足循环条件，从而决定是否继续循环或者结束程序。

2. 算例分析

2.1 计算模型

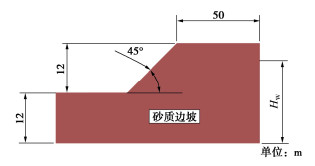
以笔者参与的某构筑物地震安全性评价项目中的饱和基坑边坡为研究对象，由于需要进行抗震加固设计，因此需要确定地震作用下的滑移面位置及主要的滑移破坏形式。土体以砂质土为主。坡长为17 m，高度约为12 m，坡度45°，概化分析模型如图 3所示。

图 3 边坡概化模型

Figure 3. Conceptual model for slope

下载: 全尺寸图片幻灯片

通过现场取样，开展了动态空心圆柱扭剪试验（图 4），并结合地质勘察报告确定了该边坡的砂质土物理力学参数取值，如表 1所示。

图 4 室内试验测试

Figure 4. Laboratory tests

下载: 全尺寸图片幻灯片

表 1 土体物理力学参数

Table 1. Physical and mechanical parameters of soils

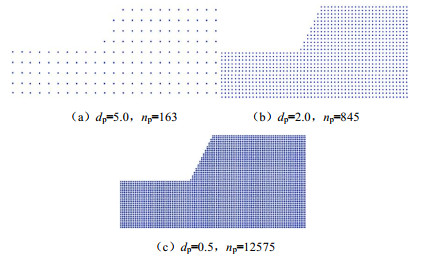
泊松比	弹性量/ MPa	重度/ (kN·m^-3)	黏聚力/ kPa	内摩擦角/(°)	残余黏聚力/ kPa	残余内摩擦角/(°)
0.3	100.4	16.8	50.42	15	5.95	15

下载: 导出CSV

| 显示表格

在SPH分析中，为了确定数值模型中粒子密度对分析结果的影响，构建了3种粒子密度不同的模型，SPH粒子的间隔d_p和每个模型所用的SPH粒子的总数n_p如图 5所示。边界条件的设定：底部为固定约束，侧面为水平向约束，垂直方向自由。模型的平滑距离h = 2.0d_p，衰减阻尼通过有限元方法首先获得该模型的第一阶和第二阶的自振频率，进而可以求出瑞利阻尼。在SPH数值积分过程中所用的时间步是通过反复试验设定，当粒子在间隔最小的情况下也能得到稳定的分析结果时候的值为1.0×10^-5 s。

图 5 SPH计算模型

Figure 5. Computational model for SPH

下载: 全尺寸图片幻灯片

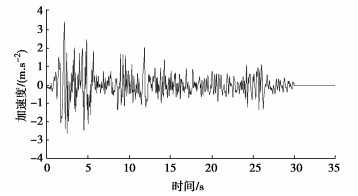
本文选用地震波为El Centro地震波，该地震波震级为7.1级，震中距为12 km，记录的最大峰值加速度为3.42 m/s²。其是用1940年位于加州南部的埃尔森特罗的一台强震仪由人类记录的第一条地震波，记录的地震动时程如图 6所示。

图 6 地震动记录

Figure 6. Ground motion recording

下载: 全尺寸图片幻灯片

2.2 边坡的应力-应变分析

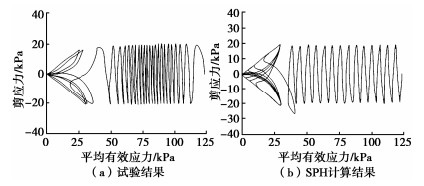
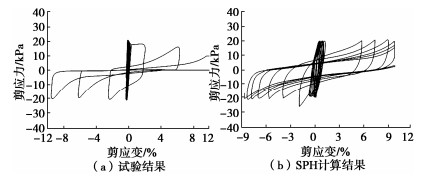
为了验证基于SPH方法的有效应力分析的合理性，针对该边坡砂质土取样（直径为50 mm，高度为100 mm），并进行了空心圆柱扭剪试验，与本文改进的SPH方法计算结果进行了对比。其中模型的粒子数为50个，粒子间距0.01 m，施加频率2 Hz的正弦波作为剪切力，时间为10 s。该循环剪切试验中的有效应力路径和剪切应力-应变关系如图 7，8所示。

图 7 有效应力路径对比

Figure 7. Comparison of effective stress paths

下载: 全尺寸图片幻灯片

图 8 剪切应力-应变关系对比

Figure 8. Comparison of shear stress-strain relationship

下载: 全尺寸图片幻灯片

由图 7，8可知，基于改进的SPH方法计算的有效应力路径和剪应力-应变关系，从初始状态到超静孔隙水压力上升、有效应力减小的过程得到了很好的再现。且有效应力归零后剪切应变急剧增加的循环滞回现象也基本上得到再现，也就是说此时土体发生了振动液化现象，有效应力降低为0，而应变会急剧增加产生大变形。从图 8还可以发现，平均主应力在25~50 kPa，SPH与试验结果差距较大，主要原因是由于动载荷作用过程中方向的改变，以及动三轴试验过程测试以及操作误差等原因，总体而言，测试值和数值结果误差在允许范围之内。另外，文中平均主应力是恒定的，排水过程中应力路径的变化对砂土的抗剪强度几乎没有影响，但会影响小变形范围内的应力-应变特性，表现为不同的弹性轨迹，可参见参考文献[1]。因此，对于模拟中的大变形影响不大。另外，剪应力-应变的循环滞回现象有一些差异，图 8（a）试验中的滞回曲线呈现V形，而图 8（b）数值方法中的滞回曲线呈现倒S形，但整体是吻合较好的。

2.3 边坡滑移面的对比分析

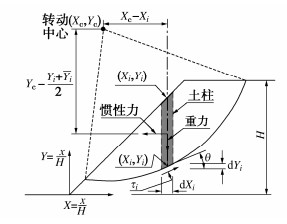
本节将通过SPH方法再现边坡的地震滑移破坏行为，确定出边坡的临界滑移面，并于与Newmark方法的对数螺旋临界滑移面形状进行对比。采用Newmark方法计算该边坡的临界滑移面。基于变分原理对边坡的对数螺旋状临界滑面的计算流程进行推导^[28]，如图 9所示。

图 9 边坡临界滑移面计算示意图

Figure 9. Calculation diagram of critical slip surface of slope

下载: 全尺寸图片幻灯片

如图 9所示，在进行边坡螺旋曲线滑移面的计算时，把滑移体简化为不同的土柱体，其相对转动中心的阻力矩和下滑力矩满足转动平衡方程：

$M = {M_{\text{R}}} - {M_{\text{D}}} = {M_R} - ({M_{{\text{DV}}}} + {M_{{\text{DH}}}}) = 0 。$

(34)

式中： ${M_{\text{R}}}$ 为滑移面的摩擦阻力矩； ${M_{\text{D}}}$ 为滑动转矩，其为滑移面土柱自重而形成的滑动转矩 ${M_{{\text{DV}}}}$ 与滑移面土柱惯性力而形成的滑动转矩 ${M_{{\text{DH}}}}$ 之和；H为边坡的高度。

以图 9中的边坡高度H为基础，建立其标准化坐标系，以坡脚为坐标原点，可以求得不同的转动力矩：

$\begin{gathered} {M_{\text{R}}} = \frac{1}{{{F_{\text{S}}}}}\sum\limits_{i = 1}^n {\left\{ {{\tau _i}\sin {\theta _i}{\text{d}}X({X_i} - {X_{\text{c}}})} \right\}} - {\tau _i}\cos {\theta _i}{\text{d}}Y({Y_{\text{c}}} - {Y_i}) \\ = \sum\limits_{i = 1}^n {({N_m} + S({Y_i}){\varphi _{\text{m}}})} [({Y_{\text{c}}} - {Y_i}) - ({X_i} - {X_{\text{c}}}){{Y'}_i}]{\text{d}}{X_i} \\ {\text{ = }}\sum\limits_{i = 1}^n {{c_{\text{m}}}} [({Y_{\text{c}}} - {Y_i}) - ({X_i} - {X_{\text{c}}}){Y'_i}]{\text{d}}{X_i} \text{，} \end{gathered}$

(35)

${M_{{\text{DV}}}} = \sum\limits_{i = 1}^n [ ({\overline Y _{\text{i}}} - {Y_i}) - ({X_i} - {X_{\text{c}}})]{\text{d}}{X_i} \text{，}$

(36)

${M_{{\text{DH}}}} = - \frac{a}{2}\sum\limits_{i = 1}^n [ ({\overline Y _{\text{i}}} - {Y_i})({Y_i}{\text{ + }}{\overline Y _{\text{i}}} - 2{Y_{\text{c}}})]{\text{d}}{X_i} \text{，}$

(37)

${X_i} = \frac{{{x_i}}}{H} \text{，} {Y_i} = \frac{{{y_i}}}{H} \text{，} {\overline Y _i} = \frac{{{{\overline y }_i}}}{H} \text{，} {Y'_i} = \frac{{{\text{d}}{Y_i}}}{{{\text{d}}{X_i}}} \text{，}$

(38)

${c_{\text{m}}} = \frac{c}{{{F_{\text{s}}}}}\cdot\frac{1}{{\gamma H}} \text{，} {\psi _{\text{m}}} = \frac{{\tan \varphi }}{{{F_{\text{s}}}}} 。$

(39)

式中：X_i，Y_i及 ${\overline Y _i}$ 分别为以边坡高H来进行标准化的滑移面位置x，y的坐标； ${\tau _i}$ 为滑移面切向剪应力；F_s为边坡稳定性安全系数； $Y'$ 为临界滑移面坐标 ${X_i}$ 的斜率；c为滑移面的黏聚力； $S({Y_i})$ 为滑移面的垂直应力； $\varphi$ 为内摩擦角； ${c_{\text{m}}}$ ， ${\varphi _{\text{m}}}$ 分别为标准化的黏聚力与内摩擦角； $\gamma$ 为滑移面上土体重度； $a$ 为作用于 ${\text{d}}{X_i}$ 区间土柱的地震加速度。

地震与地下水的耦合作用会产生超静孔隙水压力，因此在转动平衡公式（34）中需要考虑超静孔隙水压力诱发的滑移体的下滑力的作用。本文超静孔隙水压力 ${u_{{\text{sis}}}}$ 的计算式主要采用Huang等^[29]中提出的简化计算方法。临界滑移面位置处的孔隙水压力计算式为

$u = {u_0} + {u_{{\text{sis}}}} \text{，}$

(40)

式中，u为孔隙水压力， ${u_0}$ 为静孔隙水压力， ${u_{{\text{sis}}}}$ 为超静孔隙水压力。

进而转动平衡方程（40）变为

$M = {M_{\text{R}}} - {M_{\text{D}}} = {M_{\text{R}}} - ({M_{{\text{DV}}}} + {M_{{\text{DH}}}} + {M_{{\text{Du}}}}) = 0 \text{，}$

(41)

式中， ${M_{{\text{Du}}}}$ 为孔隙水压力产生的转动矩，其中 ${M_{{\text{Du}}}}$ 的表达式为

${M_{{\text{Du}}}} = \sum\limits_{i = 1}^n {\left\{ {u\cos {\theta _i}dX({X_i} - {X_c}) + u\sin {\theta _i}{d_Y}({Y_c} - {Y_i})} \right\}} 。$

(42)

对数螺旋临界滑面的形状，计算表达式为^[30]

$X = {X_c} + A\exp ( - \beta {\psi _{\text{m}}})\sin \beta \text{，}$

(43)

$Y = {Y_c} - A\exp ( - \beta {\psi _{\text{m}}})\sin \beta 。$

(44)

式中：X_C，Y_C分别为对数螺旋极坐标；A为对数螺旋常数；β为与斜面位置相关的角。此处β为以对数螺旋极坐标为中心并沿铅直方向至滑移面上的点（X，Y）的逆时针方向旋转的角。屈服加速度a_sy可由式（35）中边坡稳定性安全系数F_s为1.0时，代入平衡方程式（34）求得。

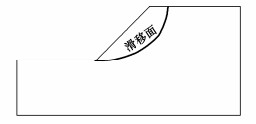
通过Newmark方法确定了边坡的临界滑移面如图 10所示。

图 10 由Newmark方法计算的滑移面

Figure 10. Slip surface calculated by Newmark method

下载: 全尺寸图片幻灯片

由图 10可知，该边坡滑移面为典型的对数螺旋形滑移面，且剪出口位于坡脚位置。

接下来采用SPH方法计算边坡滑移面形状。其中每个粒子的本构方程是有效应力模型。内摩擦角和黏聚力在首次达到断裂状态之前使用表 1中的峰值强度，之后使用残余强度值。在分析过程中，不同峰值加速度时边坡的状态是：在施加小于1 m/s²峰值加速度地震波时，边坡不会发生大的变形，在施加到2，3 m/s²峰值加速度时各个点逐渐出现位移，在施加到4 m/s²峰值加速度时，边坡内部出现滑移线，并导致完全滑坡。考虑到水平地震是边坡滑塌的主要影响因素，因此本文只考虑水平地震。

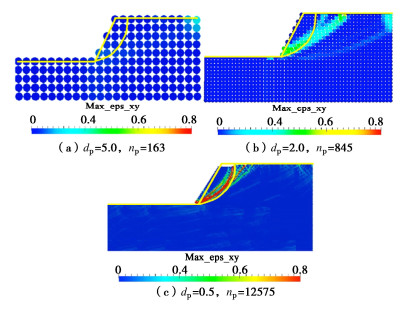
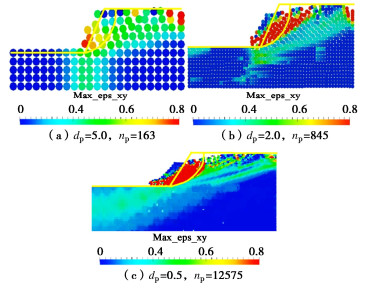
根据不同粒子密度，分别计算3个模型在地震作用下的滑移面以及滑塌模式，如图 11所示。

图 11 地震持续10 s时滑移面

Figure 11. Slip surface under earthquake at time 10 s

下载: 全尺寸图片幻灯片

如图 11所示，从地震作用开始10 s后不同模型出现的剪切应变最大的区域可以看出，在d_p为0.5 m时的滑移面与Newmark方法计算的滑移面出现位置非常相似；而d_p为2 m时剪切应变最大分布区域在坡顶面比Newmark方法位置更深的位置处。d_p为5 m时未能出现明显的滑移面。基于此，进一步计算了地震作用结束后的边坡滑移面分布情况，如图 12所示。

图 12 地震结束后滑移面

Figure 12. Slip surface after earthquake

下载: 全尺寸图片幻灯片

如图 12所示，地震作用结束后，3个模型的滑移面形状大致相同。在d_p为5，2 m的情况下剪应变最大值分布超过80%的区域几乎出现在相同的地方，与Newmark方法相比，其滑移面在接近坡顶位置更偏向内部，接近坡脚位置滑移面形状吻合较好，说明粒子密度较小的情况下，容易高估边坡的滑移规模。在d_p为0.5 m的情况下，滑移面与Newmark方法计算的滑移面整体吻合较好，且能较好地模拟边坡地震作用下滑移大变形过程。因此，在使用SPH方法进行边坡地震破坏分析中，选择合适的粒子密度是准确模拟饱和边坡地震滑移大变形的关键。分析其原因主要是由于对于SPH方法，粒子运动是由压力梯度的作用产生，粒子压力是通过状态方程由粒子自身的密度和内能来计算。SPH方法考虑了相邻粒子之间的影响作用，因此粒子的运动速度和相邻粒子的平均速度相近。在计算过程中对连续密度场的估计值会受到粒子分布的显著影响，即粒子质量分布的聚集/稀疏区域。

综上，本文改进的SPH方法可以较好地模拟饱和边坡地震临界滑移面的形状，且能再现饱和边坡地震作用下的滑移大变形过程。

3. 结论

（1）本文通过在光滑粒子流体动力学方法（SPH方法）中加入瑞利衰减阻尼，基于有效应力本构模型，对SPH方法进行了改进，建立了用于饱和边坡地震滑移大变形的数值计算方法；并将该方法与饱和土样的空心圆柱扭剪试验结果进行了对比，得出改进后的SPH方法能很好地再现饱和土体的有效应力路径和剪应力-应变滞回性能，说明其适用于饱和土体的地震大变形计算。

（2）将超静孔隙水压力简便计算方法代入Newmark方法中，确定了考虑超静孔隙水压力影响临界滑移面计算方法，并与改进的SPH方法确定的饱和边坡地震滑移临界面形状与进行了对比，得出本文改进的SPH方法能较好地再现饱和边坡地震作用下的滑移过程。

（3）分析了SPH数值计算方法中粒子密度对边坡地震滑移大变形的影响。结果表明，采用SPH方法进行边坡地震破坏分析时，结果受设置的粒子密度的影响。在dp = 0.5 m的情况下获得了非常相似的结果，而在dp = 5 m时，在滑移面的发展过程中出现了一定差异，但形状整体吻合较好。

图 1 有效应力路径

Figure 1. Effective stress path

下载: 全尺寸图片幻灯片

图 2 SPH方法的计算流程图

Figure 2. Flow chart of SPH method

下载: 全尺寸图片幻灯片

图 3 边坡概化模型

Figure 3. Conceptual model for slope

下载: 全尺寸图片幻灯片

图 4 室内试验测试

Figure 4. Laboratory tests

下载: 全尺寸图片幻灯片

图 5 SPH计算模型

Figure 5. Computational model for SPH

下载: 全尺寸图片幻灯片

图 6 地震动记录

Figure 6. Ground motion recording

下载: 全尺寸图片幻灯片

图 7 有效应力路径对比

Figure 7. Comparison of effective stress paths

下载: 全尺寸图片幻灯片

图 8 剪切应力-应变关系对比

Figure 8. Comparison of shear stress-strain relationship

下载: 全尺寸图片幻灯片

图 9 边坡临界滑移面计算示意图

Figure 9. Calculation diagram of critical slip surface of slope

下载: 全尺寸图片幻灯片

图 10 由Newmark方法计算的滑移面

Figure 10. Slip surface calculated by Newmark method

下载: 全尺寸图片幻灯片

图 11 地震持续10 s时滑移面

Figure 11. Slip surface under earthquake at time 10 s

下载: 全尺寸图片幻灯片

图 12 地震结束后滑移面

Figure 12. Slip surface after earthquake

下载: 全尺寸图片幻灯片

表 1 土体物理力学参数

Table 1 Physical and mechanical parameters of soils

泊松比弹性量/
MPa 重度/
(kN·m^-3) 黏聚力/
kPa 内摩擦角/(°) 残余黏聚力/
kPa 残余内摩擦角/(°)

0.3 100.4 16.8 50.42 15 5.95 15

下载: 导出CSV

参考文献(30)

[1]	彭孔曙, 胡敏云.有限元法在临水边坡设计中的应用[J].科技通报, 2012, 28(9): 142-146. doi: 10.3969/j.issn.1001-7119.2012.09.033 PENG Kongxu, , HU Minyun. Finite element method in the design of slope adjacent to water[J]. Bulletin of Science and Technology, 2012, 28(9): 142-146. (in Chinese) doi: 10.3969/j.issn.1001-7119.2012.09.033
[2]	ISHII Y, OTA K, KURAOKA S, et al. Evaluation of slope stability by finite element method using observed displacement of landslide[J]. Landslides, 2012, 9(3): 335-348. doi: 10.1007/s10346-011-0303-7
[3]	黄帅, 吕悦军.强震作用下动孔隙水压力对砂质边坡动力响应的影响[J].水运工程, 2015(10): 158-167. doi: 10.3969/j.issn.1002-4972.2015.10.028 HUANG Shuai, LYU Yuejun. Influence of dynamic pore water pressure on dynamic response of sandy slope under strong earthquake[J]. Port & Waterway Engineering, 2015(10): 158-167. (in Chinese) doi: 10.3969/j.issn.1002-4972.2015.10.028
[4]	董士杰, 魏红卫.地震作用下土工合成材料加筋土边坡动力分析[J].铁道科学与工程学报, 2015, 12(4): 778-783. doi: 10.3969/j.issn.1672-7029.2015.04.010 DONG Shijie, WEI Hongwei. Dynamic analysis of geosynthetic reinforced soil slope under seismic action[J]. Journal of Railway Science and Engineering, 2015, 12(4): 778-783. (in Chinese) doi: 10.3969/j.issn.1672-7029.2015.04.010
[5]	王飞, 吴红刚, 郭春香.碎石土路堑高边坡地震动力响应过程分析[J].中国地质灾害与防治学报, 2020, 31(1): 18-24. doi: 10.16031/j.cnki.issn.1003-8035.2020.01.03 WANG Fei, WU Honggang, GUO Chunxiang. Dynamic response of high cut based a numerical simulation slope to earthquake[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(1): 18-24. (in Chinese) doi: 10.16031/j.cnki.issn.1003-8035.2020.01.03
[6]	YIN Y P, LI B, WANG W P. Dynamic analysis of the stabilized Wangjiayan landslide in the Wenchuan Ms 8.0 earthquake and aftershocks[J]. Landslides, 2015, 12(3): 537-547. doi: 10.1007/s10346-014-0497-6
[7]	WU H, ATANGANA NJOCK P G, CHEN J J, et al. Numerical simulation of spudcan-soil interaction using an improved smoothed particle hydrodynamics (SPH) method[J]. Marine Structures, 2019, 66: 213-226. doi: 10.1016/j.marstruc.2019.04.007
[8]	BUI H H, FUKAGAWA R, SAKO K, et al. Slope stability analysis and discontinuous slope failure simulation by elasto-plastic smoothed particle hydrodynamics (SPH)[J]. Géotechnique, 2011, 61(7): 565-574. doi: 10.1680/geot.9.P.046
[9]	HUANG Y, ZHANG W J, XU Q, et al. Run-out analysis of flow-like landslides triggered by the Ms 8.0 2008 Wenchuan earthquake using smoothed particle hydrodynamics[J]. Landslides, 2012, 9(2): 275-283. doi: 10.1007/s10346-011-0285-5
[10]	唐宇峰, 施富强, 廖学燕.基于SPH的边坡稳定性计算中失稳判据研究[J].岩土工程学报, 2016, 38(5): 904-908. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16564.shtml TANG Yufeng, SHI Fuqiang, LIAO Xueyan. Failure criteria based on SPH slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 904-908. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16564.shtml
[11]	NONOYAMA H, MORIGUCHI S, SAWADA K, et al. Slope stability analysis using smoothed particle hydrodynamics (SPH) method[J]. Soils and Foundations, 2015, 55(2): 458-470. doi: 10.1016/j.sandf.2015.02.019
[12]	ZHANG Z Y, JIN X G, BI J. Development of an SPH-based method to simulate the progressive failure of cohesive soil slope[J]. Environmental Earth Sciences, 2019, 78(17): 537. doi: 10.1007/s12665-019-8507-6
[13]	张卫杰, 高玉峰, 黄雨, 等.水土耦合SPH数值模型的正则化修正及其应用[J].岩土工程学报, 2018, 40(2): 262-269. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17280.shtml ZHANG Weijie, GAO Yufeng, HUANG Yu, et al. Normalized correction of soil-water-coupled SPH model and its application[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 262-269. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17280.shtml
[14]	张卫杰, 郑虎, 王占彬, 等.基于三维并行SPH模型的土体流滑特性研究[J].工程地质学报, 2018, 26(5): 1279-1284. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201805021.htm ZHANG Weijie, ZHENG Hu, WANG Zhanbin, et al. Study on flowing behavior of soil based on three dimen-sional and parallelized sph model[J]. Journal of Engineering Geology, 2018, 26(5): 1279-1284. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201805021.htm
[15]	DAI Z L, HUANG Y, CHENG H L, et al. 3D numerical modeling using smoothed particle hydrodynamics of flow-like landslide propagation triggered by the 2008 Wenchuan earthquake[J]. Engineering Geology, 2014, 180: 21-33. doi: 10.1016/j.enggeo.2014.03.018
[16]	HUANG Y, DAI Z L. Large deformation and failure simulations for geo-disasters using smoothed particle hydrodynamics method[J]. Engineering Geology, 2014, 168: 86-97. doi: 10.1016/j.enggeo.2013.10.022
[17]	FULK D A. A numerical analysis of smoothed particle hydrodynamics[D]. Wright-Patterson AFB: Thesis Air Force Inst Tech, 1994.
[18]	LIU G R, LIU M B. Smoothed Particle Hydrodynamics-A Meshfree Particle Method[M]. Singapore: World Scientific Publishing Co Pte Ltd, 2003.
[19]	MAO Z, LIU G R, DONG X. A comprehensive study on the parameters setting in smoothed particle hydrodynamics (SPH) method applied to hydrodynamics problems. Computers and Geotechnics, 2017, 92: 77-95. doi: 10.1016/j.compgeo.2017.07.024
[20]	岩本哲也, 小野祐輔.弾性波伝播問題に対する粒子法の適用性[J].応用力学論文集, 2009, 12: 611-622. TETSUYA I, YUSUKE O. Applicability of meshfree particle method to elastic wave propagation analysis[J]. Journal of Applied Mechanics, 2009, 12: 611-622. (in Japanese)
[21]	CHEN J K, BERAUN J E, JIH C J. Completeness of corrective smoothed particle method for linear elastodynamics[J]. Computational Mechanics, 1999, 24(4): 273-285.
[22]	马红权, 张学莹. SPH的核近似和粒子近似[J].信息技术, 2012, 36(7): 170-171,175. https://www.cnki.com.cn/Article/CJFDTOTAL-HDZJ201207049.htm MA Hongquan, ZHANG Xueying. Kernel approximation and particle approximation about SPH[J]. Information Technology, 2012, 36(7): 170-171,175. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HDZJ201207049.htm
[23]	社本康広, 時松孝次, 有泉浩蔵.一次元有効応力解析の実地盤に対する適用性[J].日本建築学会構造系論文報告集, 1992, 433: 113-119. YDSUHIRO S, KOHJI T, KOUXO A. Applicability of a one-dimensional effective stress analysis to an existing soil deposit[J]. Journal of Structure Construction Engineering, 1992, 433: 113-119. (in Japanese)
[24]	JENNINGS P C. Periodic response of a general yielding structure[J]. Journal of the Engineering Mechanics Division, 1964, 90(2): 131-166.
[25]	GRAY J P, MONAGHAN J J, SWIFT R P. SPH elastic dynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(49): 6641-6662.
[26]	HA H, BUI K, SAKO R, et al. Numerical simulation of soil–water interaction using smoothed particle hydrodynamics (SPH) method[J]. Journal of Terramechanics, 2007, 44(5): 339-346.
[27]	冷艺, 栾茂田, 许成顺, 等.应力历史对饱和砂土力学性状影响的试验研究[J].岩土力学, 2009, 30(5): 1257-1263. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200905012.htm LENG Yi, LUAN Maotian, XU Chengshun, et al. Experimental study of effect of stress history on mechanical properties of saturated sand under complex stress conditions[J]. Rock and Soil Mechanics, 2009, 30(5): 1257-1263. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200905012.htm
[28]	黄帅, 宋波, 牛立超, 等.地震作用下动孔隙水压力对边坡永久位移影响的简便计算方法[J].建筑结构学报, 2014, 35(3): 215-221. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201403028.htm HUANG Shuai, SONG Bo, NIU Lichao, et al. Simple calculation method of permanent displacement of slope influenced by dynamic pore water pressure under earthquake[J]. Journal of Building Structures, 2014, 35(3): 215-221. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201403028.htm
[29]	HUANG S, LYU Y J, SHA H J, et al. Seismic performance assessment of unsaturated soil slope in different groundwater levels[J]. Landslides, 2021, 18: 2813-2833.
[30]	霍沿东.基于极限分析上限方法的海底黏性土边坡地震稳定性评[D].大连: 大连理工大学, 2018. HUO Yandong. Evaluation of Seismic Stability of Submarine Clay Slopes Based on Upper Bound Approach of Limit Analysis[D]. Dalian: Dalian University of Technology, 2018. (in Chinese)

施引文献(7)

期刊类型引用(3)

1.	黄帅，王中根，李昱，冯宇翔. 基于改进SPH方法的滑坡涌浪对大坝结构冲击响应规律. 工程科学与技术. 2025(01): 120-131 . 百度学术
2.	魏星，程世涛，谢相焱，陈睿. 考虑强度速率衰减效应的地震滑坡SPH-FEM模拟. 岩土工程学报. 2024(08): 1753-1761 . 本站查看
3.	郑厚国，周永强，刘烨. 高水头作用下饱和边坡破坏物质点法模拟研究. 能源与环保. 2023(05): 276-283+288 . 百度学术