裂隙-孔隙双重介质Darcy-Forchheimer耦合流动模拟方法及工程应用

熊峰; 姜清辉; 陈胜云; 胡小川

doi:10.11779/CJGE202111010

裂隙-孔隙双重介质Darcy-Forchheimer耦合流动模拟方法及工程应用 English Version

熊峰^1,,
姜清辉²,
陈胜云^3, ,,
胡小川⁴

1.
中国地质大学（武汉）工程学院,湖北　武汉　430074
2.
武汉大学土木建筑工程学院,湖北　武汉　430072
3.
中国人民解放军军事科学院国防工程研究院,北京　100850
4.
中建二局土木工程集团有限公司,北京　101100

基金项目:

国家自然科学基金面上项目 42077243

中国人民解放军军事科学院国防工程研究院资助项目 2019-JKGF-1043

详细信息

作者简介:
熊峰(1992— ),男,副教授,博士,从事裂隙岩体渗流的教学和科研工作。E-mail：fengxiong@cug.edu.cn

通讯作者:
陈胜云, E-mail：chenshengyunjia@163.com

中图分类号: TU43
计量
- 文章访问数: 326
- HTML全文浏览量: 40
- PDF下载量: 176
出版历程
- 收稿日期: 2021-03-22
- 网络出版日期: 2022-12-01
- 刊出日期: 2021-10-31

Modeling of coupled Darcy-Forchheimer flow in fractured porous media and its engineering application

1.
Faculty of Engineering, China University of Geosciences (Wuhan), Wuhan 430074, China
2.
School of Civil Engineering, Wuhan University, Wuhan 430072, China
3.
Inst. of Defence Eng., AMS, PLA, Beijing 100850, China
4.
The Civil Engineering Group Corporation of China Second Engineering Bureau Ltd., Beijing 101100, China

摘要

摘要: 针对裂隙-孔隙双重介质非线性渗流问题,采用压力交换函数描述孔隙Darcy渗流和裂隙Forchheimer渗流耦合特性,推导了渗流方程有限体积的数值格式,并编制了相应的计算程序。通过与单裂隙和相交裂隙渗流的Frih和Arraras解对比,验证了新方法的合理性。对富水深埋裂隙型围岩隧道非线性渗流问题的计算表明,所提算法对复杂裂隙系统问题具有很强的适用性。进一步分析隧道围岩渗流特征：越接近隧道位置,水压梯度越大,流量也越大；隧道周围水压梯度呈现“底部大,顶部小”的特点,最大相差2.5倍,因此隧道底部的流量大于顶部流量；裂隙方向均匀性和密度是影响隧道围岩水力特性的重要因素。在一定水力梯度下,裂隙方向越集中于水力梯度方向且密度越大时,围岩导水性越大,隧道流量越大,越容易发生涌水事故。研究成果为裂隙型围岩隧道防水设计及工程实践提供参考。
- 裂隙-孔隙双重介质 /
- Darcy-Forchheimer耦合流动 /
- 有限体积法 /
- 隧道非线性渗流
Abstract: Aiming to solve the nonlinear flow in fractured porous media, the coupling characteristics between Darcy flow in pores and Forchheimer flow in fractures are described by means of the pressure transfer function. The finite volume numerical form of seepage equations is derived, and the corresponding numerical code is written. The flow solution by the proposed method for single fracture and intersecting fracture is verified against Frih and Arraras’ solution. Based on this method, the fluid flow behavior of a fractured rock deep-buried tunnel is simulated, which shows it has strong applicability to flow in complex fracture system. The nonlinear flow of tunnel is also analyzed. The results show that the hydraulic gradient of surrounding rock is characterized by "large at bottom and small at top", with the maximum difference of 2.5 times. Therefore, the flow rate at the bottom of the tunnel is greater than that at the top. The distribution homogeneity and density of fracture are the important factors that affect the hydraulic behavior of fractured rock tunnels. At certain water pressure, the more fractures concentrated in the direction of water pressure and the greater the density is, the greater the surrounding rock conductivity is and the greater the flow rate of tunnel is. In this condition, water-inflow accident of tunnels will be prone to occur. The research results may provide reference for the waterproof design and engineering practice of fractured rock tunnels.
- fractured porous medium /
- coupled Darcy-Forchheimer flow /
- finite volume method /
- nonlinear flow in tunnel

HTML全文

0. 引言

矿山、石油、水力水电、地热开采等工程无不涉及岩体渗流问题。①岩体裂隙渗透率高,流体在裂隙中快速流动；②岩块渗透率较低,流体也会缓慢通过岩块中微小孔隙,两者相互作用,存在着复杂的耦合过程。因此,建立有效的岩体渗流模型仍然充满着挑战。自20世纪70年代,基于裂隙特性和分布规律的认识,各种岩体渗流模型相继被提出^[1]。

连续介质模型（continuum media model）^[2-6]适用于岩体中含大量规则分布的微小裂隙。基于均质理论,以渗流系数张量理论、广义达西定律和流体连续性方程为基础,推导得到流量和压力的偏微分方程。通过初始条件和边界来求解该偏微分方程组,得到整个流场的速度场和压力场。但当研究区域存在多个大型断层或者不连续面时,采用等效连续介质模型的合理性有待商榷。离散裂隙网络模型（fracture network model）^[7-10]仅考虑岩体中宏观裂隙的渗流情况,这些裂隙通常根据裂隙的产状、大小、水文参数等随机生成。以各裂隙交叉点处的流量平衡原理建立控制方程,然后结合单裂隙流动方程,得到压力与流量的矩阵方程。最后求解该方程组,得到速度场和压力场。离散裂隙网络模型适用于岩体内分布较为稀疏的大规模裂隙。但它不考虑岩块的流动情况,在某些高孔隙率的岩体中,可能误差较大。裂隙-孔隙双重介质模型（fractured porous model）^[11-13]最早由Barenblatt等提出的,将裂隙岩体的分为孔隙系统和裂隙系统,广义模型认为相互连通的裂隙是流体流动的通道的,而孔隙和孤立的裂隙是储存流体的,两者在相互连通的裂隙壁上进行流量交换,满足流量守恒定律。流体在岩体中流动存在着优先流特征。这种特性是指水绕过岩石基质优先进入裂隙中。裂隙开度的不均匀性,使得流动以局部化指流推进,而不是充满整个裂隙空间^[14-15]。因此,与连续介质模型和离散裂隙介质相比,双重介质模型考虑了基质与裂隙渗透性的差异,能够较准确的刻画优先流现象。同时考虑了水流的交换作用,使得模拟具有较好的拟真性。张奇华等^[13]总结了现有的两种双重介质渗流计算方法的特点,即整体求解法和流量交换法。流量交换法在处理发育程度高的裂隙方面更有优势。

在早期,双重介质模型假设流体在裂隙或孔隙介质流动符合Darcy定律。Darcy定律已被证明在流速较低的状态下符合多孔介质单相不可压缩流动,例如渗透率低的地下岩体含水储层。然而,在钻井口或者高渗透率裂隙区域中,流速较高,Darcy定律并不适用。为了描述高流速下渗流规律,最简单的方式之一是在Darcy定律的基础上增加二次修正项,得到了被广泛采用的Forchheimer定律。该定律结合了黏滞效应和惯性效应：在低流量时,黏滞效应占主导地位,模型简化为Darcy定律；增加流量时,惯性效应占主导定位,使得压力随流量呈非线性增加。

对于裂隙和孔隙的Darcy流,双重介质模拟方法主要难点是n维（n=2,3）孔隙介质流动与n-1维裂隙的耦合难题。近些年来,许多学者对该问题展开了深入研究,例如,Lang等^[16]基于双重介质理论,提出了一种裂隙-孔隙双重介质全渗透张量的计算方法。蒋中明等^[17]采用裂隙单元来考虑裂隙渗流对岩体渗流的贡献,发展了双重介质嵌入裂隙连续方法（embedded fractured continuum）。然而,考虑高渗压下裂隙的Forchheimer流的双重介质渗流模拟少有报道。该问题主要难点在于裂隙离散化后非线性系统的求解问题。其中,Frih等^[18]采用了接触模型（interface model）处理裂隙,在接触处添加非线性传递条件,使用区域分解技术将该问题简化成（n-1）维的非线性系统问题。Arrars等^[19]采用了多重网格法来计算非线性系统问题,并讨论对于双重介质Darcy-Forchheimer流动非线性系统的鲁棒性。结果表明,该算法严重依赖于网格大小和Forchheimer系数。

本文在前人研究基础上,考虑了裂隙介质的Forchheimer流动和孔隙的Darcy流动,采用有限体积法,推导了Forchheimer和Darcy方程的数值格式,采用压力交换函数描述两者的耦合效应,编制了相应的模拟程序。通过2个算例验证了该方法的正确性,最后基于该程序进一步探讨了裂隙方向均匀性和密度对隧道围岩非线性渗流的影响机制。该方法为双重介质Darcy-Forchheimer耦合流动模拟提供了一个新的思路。

1. 控制方程

1.1 孔隙介质渗流方程

地下水在均质孔隙基质中渗流速度缓慢,遵循Darcy定律,且假定流体不可压缩,其流体在孔隙基质中流动的质量和动量守恒方程为

$u_{m} = - \frac{k_{m}}{μ} \nabla p_{m}$ ,

(1)

$\nabla u_{m} = q_{m}$ ,

(2)

式中, $u_{m}$ 为孔隙介质渗流速度,k_m为孔隙介质渗透系数,μ为流体的黏滞系数,p_m为孔隙介质流体压力,q_m为孔隙介质汇源项。

1.2 裂隙介质渗流方程

在高水力梯度下,地下水在裂隙中流动速度较快,可采用Forchheimer定律描述。其流体在裂隙中压力梯度和流速的关系如下^[20]：

$(1 + β | u_{f} |) u_{f} = - \frac{k_{f}}{μ} \nabla p_{f}$ ,

(3)

$\nabla u_{f} = q_{f}$ ,

(4)

式中,u_f为裂隙介质渗流速度,k_f为裂隙介质渗透系数,μ为流体的黏滞系数,p_f为裂隙介质压力,q_f为裂隙介质汇源项,β为Forchheimer系数。

为考虑孔隙介质和裂隙介质流量相互交换的作用,引入交换函数Ψ来说明两者的相互影响。孔隙介质和裂隙介质流量交换的强弱与流体特性以及裂隙连通性有关,因此,压力的交换函数可定义如下：

$Ψ^{fm} = CI \times \frac{k_{m}}{μ} \times \frac{p_{f} - p_{m}}{L}$ ,

(5)

$Ψ^{mf} = C I \times \frac{k_{f}}{μ} \times \frac{p_{m} - p_{f}}{A}$ 。

(6)

因此, $Ψ^{f m}$ , $Ψ^{m f}$ 满足如下关系：

$\int Ψ^{m f} d A = - \int Ψ^{f m} d L$ ,

(7)

式中,CI为裂隙的连通度,L,A分别为裂隙的面积（长度）和孔隙的体积（面积）。连通度CI采用Hajibeygi等^[21]定义,表达式为

$C I_{ij, k} = \frac{A_{i j, k}}{{\bar{d}}_{i j, k}}$ ,

(8)

式中,A_ij,_k为孔隙基质单元ij中裂隙k的总长度, ${\bar{d}}_{i j, k}$ 为裂隙单元k和孔隙基质单元ij中的平均距离,如图1所示：

${\bar{d}}_{i j, k} = \frac{\int l_{k} d A}{A_{i j}}$ 。

(9)

图 1 裂隙-孔隙双重介质离散示意图

Figure 1. Schematic diagram of fractured porous media

下载: 全尺寸图片幻灯片

对该式展开,得到二重积分表达式：

(10)

式中,(x'_ko, y'_ko)为裂隙单元k在局部坐标系下的中心坐标。式（9）一般在小部分情况下有解析表达式,而大部分情况必须采用数值方法求解。Hajibeygi等^[21]给出了部分情况下的解析表达式。

将流量交换函数代入式（1）～（4）,得到孔隙和裂隙渗流方程：

$q_{m} + \nabla (\frac{k_{m}}{μ} \nabla p_{m}) + Ψ^{mf} = 0$ ,

(11)

$\nabla \frac{k_{f}}{μ} \nabla p_{f} + (1 + β | u_{f} |) u_{f} + Ψ^{fm} = 0$ 。

(12)

2. 数值算法

2.1 有限体积法数值格式

（1）孔隙介质渗流方程数值格式

将孔隙介质流域Ω离散成矩形单元Ω_ij,如图1所示。对孔隙介质渗流方程进行积分,使用高斯理论,式（11）的体积分可以转化为垂直于体外面的面积分：

$\begin{matrix} \int_{Ω_{ij}} (q_{m} + \nabla (\frac{k_{m}}{μ} \nabla p_{m}) + Ψ^{m f}) d V \Rightarrow \\ \int_{\partial Ω_{ij}} (\frac{k_{m}}{μ} \nabla p_{m} + Ψ^{m f}) n d s + \int_{Ω_{ij}} q_{m} d V \end{matrix}$ 。

(13)

采用有限体积法,得到每个单元Ω_ij渗流方程的中心差分数值形式：

$\begin{matrix} \frac{Δ y {(\frac{k}{μ})}_{i, j}^{m}}{Δ x} (p_{i, j}^{m} - p_{i - 1, j}^{m}) + \frac{Δ y {(\frac{k}{μ})}_{i, j}^{m}}{Δ x} (p_{i, j}^{m} - p_{i + 1, j}^{m}) + \\ \frac{Δ x {(\frac{k}{μ})}_{i, j}^{m}}{Δ y} (p_{i, j}^{m} - p_{i, j - 1}^{m}) + \frac{Δ x {(\frac{k}{μ})}_{i, j}^{m}}{Δ y} (p_{i, j}^{m} - p_{i, j + 1}^{m}) + \\ q_{i j}^{m} Δ x Δ y + \sum_{Ω_{i j} \cap Ω_{k}} {CI}_{k} {(\frac{k}{μ})}_{i j, k} (p_{k}^{f} - p_{i j}^{m}) = 0 \end{matrix}$ 。

(14)

（2）裂隙介质渗流方程数值格式

同理,采用一维线单元离散裂隙,运用有限体积法,得到每个单元渗流方程式（12）的中心差分数值形式为

$\begin{array}{l} \frac{b_{k} {(\frac{k}{μ})}_{k}^{f}}{Δ x^{f}} (p_{k}^{f} - p_{k - 1}^{f}) + \frac{b_{k} {(\frac{k}{μ})}_{k}^{f}}{Δ x^{f}} (p_{k}^{f} - p_{k + 1}^{f}) + \\ (1+ β | u_{f} |) q_{i j}^{m} b Δ x^{f} - \sum_{Ω_{i j} \cap Ω_{k}} {CI}_{k} {(\frac{k}{μ})}_{i j, k} (p_{k}^{f} - p_{i j}^{m}) = 0 。 \end{array}$

(15)

2.2 相交裂隙处理

当流体通过相交裂隙后,会导致流体水头损失,影响着整个区域的渗流行为。Xiong等^[22]开展了交叉裂隙渗流试验,讨论了相交裂隙水头损失问题,并指出相交裂隙水头损失不可忽略。因此,为了考虑相交裂隙对水头的影响,Karimi等^[23]采用下式计算两个相交裂隙（i和j）的导水率T_ij：

$T_{i j} = \frac{U_{i} \times U_{j}}{U_{i} + U_{j}}$ ,

(16)

$\begin{array}{l} U_{i} = \frac{k_{f i}}{μ} \frac{b_{i}}{0 .5 Δ x_{f}} ， \\ U_{j} = \frac{k_{f i}}{μ} \frac{b_{j}}{0 .5 Δ x_{f}} ， \end{array}}$

(17)

式中,Δx_f为裂隙单元的长度,b_i,b_j分别为裂隙i和j的开度。

2.3 求解策略

按照有限体积法求解步骤,通过组装每个单元的压力离散方程,包括孔隙介质和裂隙介质压力方程,最后得到一个大型的稀疏方程组T·x=A。系数矩阵T为

$T = (\begin{matrix} T^{m m} & T^{m f} \\ T^{f m} & T^{f f} \end{matrix})$ 。

(18)

式中T^mm为孔隙区域传导矩阵；T^ff为裂隙的传导矩阵,包括裂隙和裂隙交叉处的传导系数；T^mf,T^fm为孔隙-裂隙交换传导矩阵和裂隙-孔隙交换传导矩阵。值得注意的是,裂隙传导矩阵T^ff是一个关于流速的函数,因此组装得到的方程组是一个非线性方程组。为了求解该方程组,采用直接迭代算法求解。

一个大型非线性方程组可以写为

$K (δ) δ - R = 0$ ,

(19)

式中,K为系数矩阵, $δ$ 为未知数向量,R为常系数向量。

假设初始解为 $δ = δ_{0}$ ,因此一个近似解可以得到：

$K_{0} = K (δ)$ ,

(20)

$δ_{1} = {[K_{0}]}^{- 1} R$ 。

(21)

重复上述过程,得到i+1步近似解为

$δ_{i + 1} = {[K (δ_{i})]}^{- 1} R$ 。

(22)

当||δ_i+1-δ_i||小于指定的容差要求时,近似解收敛于最终解,迭代终止。这时,δ_i+1为非线性方程组的解。通过多次的试算,容差取为10^-6。每一步迭代采用预处理共轭梯度法求解线性方程组。

基于上述计算方法,利用MATLAB编程功能设计了裂隙-孔隙双重介质非线性渗流程序。其中,网格划分方法如下,对于孔隙计算域采用均匀布点法离散成矩形单元,裂隙采用均匀分段法划分成一维线单元。

3. 算例验证

3.1 单裂隙算例

所考察的算例来自Frih等^[18]和Arraras等^[19]报道。该模型为2 m×1 m的长方形区域,中间位置为一开度0.01 m的竖直裂隙。孔隙区域渗透系数k_m为10^-9 m²,裂隙渗透系数为10^-7 m²。孔隙区域左右边界分别设置水压为10⁶,0 Pa,裂隙上下边界水压为10⁶,0 Pa,其他边界为无流量边界,如图2所示。流体的密度为1000 kg/m³,黏滞系数为0.001 Pa·s。为了说明所提方法的精确性,采用误差指标e来表示新方法与Frih等^[18]和Arraras等^[19]解的差异：

$e= \frac{\sum {(p_{新方法} - p_{F or A})}^{2}}{\sum {(p_{F or A})}^{2}} \times 100 %$ ,

(23)

图 2 算例1计算模型

Figure 2. Computational model for single fracture

下载: 全尺寸图片幻灯片

式中,p_新方法为新方法计算的压力分布,p_{F or A}为Frih等^[18]和Arraras等^[19]计算的压力分布。首先,模拟了非线性参数β=10,网格尺寸为0.02 m模型的压力分布。图3为新方法计算得到的压力分布。计算得到的压力分布与Frih等^[18]和Arrars等^[19]计算结果是一致的。图4为裂隙速度分布,速度呈现“两头大,中间低”的特点,与压力分布规律一致。

图 3 本文模型计算的压力分布

Figure 3. Distribution of pressure calculated by proposed method

下载: 全尺寸图片幻灯片

图 4 单裂隙模型的裂隙速度分布

Figure 4. Distribution of fracture velocity of single fracture model

下载: 全尺寸图片幻灯片

另外,考察不同网格大小对压力求解精度的影响,图5为网格尺寸h与新方法计算误差指标e的关系,从图中可以看出,对于所考察的网格尺寸范围,随着网格尺寸的增加,计算误差指标e从0.8%增加到8%,趋势呈现先缓慢增长,当单元尺寸达到0.02 m时,开始急剧增加。网格尺寸小于0.02 m,误差小于1%,且对于所有网格尺寸,误差指标都小于10%。这表明,新方法在描述单裂隙-孔隙介质区域渗流行为方面具有足够的精度。另外讨论了网格大小对计算时间的影响,如图6所示。随着网格尺寸的增加,计算时间剧烈减小,当网格尺寸达到0.02 m后,开始保持稳定。对于所有的网格尺寸,计算时间保持在2～3 s。

图 5 算例1网格大小与误差的关系

Figure 5. Relationship between error and mesh size

下载: 全尺寸图片幻灯片

图 6 算例1单元比率与误差的关系

Figure 6. Relationship between error and element ratio

下载: 全尺寸图片幻灯片

最后考察了网格形状对计算精度的影响,由于采用的是矩形单元,定义单元比率e-ratio为长边与短边的比值,绘制了单元尺寸为0.005 m不同单元比率与误差的关系,见图6所示。从图中可以看出,随着e-ratio的增加,e_F,e_A逐步增加,当e-ratio达到4时,误差超过了10%,此时新方法计算的结果误差较大。e-ratio为1时,误差小于1%。

3.2 相交裂隙算例

所选两个算例来自于Frih等^[18]报道。两个模型为2 m×1 m的长方形区域,模型1包含4条开度为0.01 m的裂隙,裂隙相交于一点T₁。模型2包含5条开度为0.01 m的裂隙,裂隙相交于点T₂和T₃。孔隙和裂隙区域的计算参数与算例1一致。边界条件如下：孔隙区域左右边界分别设置水压为10⁶,0 Pa,裂隙上下边界水压为10⁶,0 Pa,其他边界为无流量边界,如图7（a）,（b）所示。首先,模拟了非线性参数β=10,网格尺寸为0.02 m模型的压力分布。图8,9为新方法和计算得到的压力分布。相交裂隙1,2计算得到的压力分布与Frih等^[18]计算结果是一致的。进一步比较可知,新方法计算的压力略高于Frih等^[18]的结果。一方面Frih等^[18]未考虑裂隙交叉位置的水头损失,认为在交叉裂隙水头相等,而新方法采用了Karimi等^[23]人提出的交叉裂隙导水率公式；另一方面采用的网格尺寸较大,影响了计算精度。

图 7 相交裂隙计算模型

Figure 7. Computational model for intersecting fracture

下载: 全尺寸图片幻灯片

图 8 相交裂隙1新方法计算的压力

Figure 8. Distribution of pressure calculated by proposed method for intersecting fracture case 1

下载: 全尺寸图片幻灯片

图 9 相交裂隙2新方法计算的压力

Figure 9. Distribution of pressure calculated by proposed method for intersecting fracture case 2

下载: 全尺寸图片幻灯片

另外,考察不同网格大小对压力求解精度的影响,图10为网格尺寸h与新方法计算误差指标e的关系,从图中可以看出,对于所考察的网格尺寸范围,随着网格尺寸的增加,计算误差指标e从0.6%增加到12%。当网格尺寸小于0.01 m时,误差指标小于1%,这表明,新方法能够描述交叉裂隙-孔隙介质区域非线性渗流行为。同样,讨论了网格大小对计算时间的影响,如图10所示。随着网格尺寸的增加,计算时间逐步减小,当网格尺寸达到0.02 m后,开始保持稳定。对于所有的网格尺寸,计算时间保持在2.4～3.2 s。综合单裂隙和相交裂隙计算时间,新方法具有较高的计算效率。

图 10 相交裂隙网格大小与误差的关系

Figure 10. Relationship between error and mesh size for intersecting fracture model

下载: 全尺寸图片幻灯片

最后考察了网格形状对计算精度的影响,绘制了单元尺寸为0.005 m不同单元比率与误差的关系,见图11所示。从图中可以看出,随着e-ratio的增加,模型1和模型2 e_F逐步增加,当e-ratio达到4时,误差超过了10%,此时新方法计算的结果误差较大。e-ratio为1时,误差小于1%。综合单裂隙和相交裂隙单元比率的影响,e-ratio小于4时,新方法模拟结果可接受。

图 11 相交裂隙单元比率与误差的关系

Figure 11. Relationshp between error and mesh ratio for intersecting fracture model

下载: 全尺寸图片幻灯片

4. 隧道围岩非线性渗流分析

4.1 模型设置及计算参数

港珠澳大桥珠海连接线南湾隧道围岩较破碎,且水压较大,是典型的富水深埋隧道,建立的数值模型如图12所示。将整个计算区域划分成1×10⁶个四边形单元,总节点数为10201个,单元尺寸为0.8 m,单元比率为1。根据现场地质条件,并考虑到边界的影响,整个计算模型长80 m,高80 m。隧道为圆形隧道,半径为3 m,圆心坐标为（40,40）。隧道未考虑支护措施,实施体内排水,因此隧道水压p为0。计算参数选取工程地质报告,水的密度取1000 kg/m³,岩体渗透系数为1×10^-8 m²,孔隙率为0.3,裂隙渗透系数为1×10^-5 m²；流体的黏度为10×10^-3 Pa*s,Forchheimer系数取50。

图 12 隧道模型尺寸及边界条件

Figure 12. Dimension and boundary of tunnel model

下载: 全尺寸图片幻灯片

在模拟中,假设围岩远场地下水补给充分,地下水面不随隧道排水而降低,因此,地面水位保持恒定,水压为0。隧道渗流场在重力作用下沿数值方向呈线性分布,梯度为流体重度,因此,底部水压为8×10⁵ Pa（80 m水头）,两侧水压设置线性水压,如图11所示。

为了简化计算,隧道模型中未考虑地层、断层等地质结构,只模拟了围岩随机裂隙的影响。裂隙模型采用随机Mento-Carlo方法生成。裂隙的位置服从均匀分布,裂隙的长度服从指数分布：

$f (l) = λ e^{(- λ l)}$ ,

(24)

式中, $f (l)$ 为裂隙长度的概率密度函数, $λ$ 为指数分布参数。裂隙的长度在[l_min,l_max]之间取值。另外一个重要的参数是裂隙的方向,在三维裂隙中指的是裂隙的倾向和倾角,而在二维裂隙系统中,可以用裂隙的倾角θ来表示。裂隙的倾角θ可用von-Mises分布来模拟：

$f (θ) = \frac{e^{κ c o s (θ - μ)}}{2 π I_{0} (κ)}$ ,

(25)

$I_{n} (κ) = \frac{1}{π} \int_{0}^{π} e^{κ c o s (x)} c o s (n x) d x$ ,

(26)

式中,μ为裂隙倾角的均值,κ为von-Mises分布系数,表征了裂隙方向分布的不均匀性。根据地质勘查的资料,裂隙参数如表1所示。

表 1 裂隙几何参数

Table 1. Geometrical parameters of fractures

长度/m		开度/mm		倾角		数量N
l_min	l_max	λ	b	μ	κ	数量N
1.0	60.0	1.0	0.1	50°	[0,8]	[10,300]

下载: 导出CSV

| 显示表格

4.2 计算结果及讨论

基于裂隙-孔隙双重介质非线性渗流数值方法,研究了裂隙的不均匀性和密度对南湾裂隙型围岩隧道突涌水流态演化和涌水量的影响。

（1）裂隙方向不均匀性影响

为了探究裂隙方向不均匀性的影响,模拟裂隙参数κ取为0,1,2,4,8,16。κ越大,表示裂隙分布越不均匀。其他参数如表1所示。

取x=40的隧道中心线y=[30,50]段水压,绘制不同κ值水压分布见图13。靠近隧道底部水压变化较大,平均梯度达到8300 Pa/m,而靠近隧道顶部的水压变化较小,平均梯度为3300 Pa/m。这表明,隧道底部的流量高于隧道顶部。另外,当κ值越大时,隧道周围水压梯度越大。但对隧道底部围岩影响小于隧道顶部。这进一步说明裂隙方向越集中于水力梯度方向,隧道流量将越大。

图 13 不同κ值下隧道围岩[30, 50]段压力分布

Figure 13. Distribution of water pressure of tunnel rock at [30, 50] range under different values of κ

下载: 全尺寸图片幻灯片

图14为不同κ值下裂隙网络的流量分布,从图中看出,裂隙流量分布具有明显的不均匀性特征,主要表现为,顺着流动方向（y轴向下）的裂隙流量大,垂直流动方向（x轴）的流量较小,最大流量是最小流量的60倍左右。最大的裂隙流量分布于靠近隧道位置,为1×10^-6～2×10^-6 m³/s/m,主要原因是在隧道出口处,水力梯度较大,这与上述水压规律分析结果是一致的。

图 14 不同κ值下裂隙流量分布

Figure 14. Distribution of fracture flow rate under different values of κ

下载: 全尺寸图片幻灯片

（2）裂隙密度影响

通过改变裂隙数量来分析裂隙密度对隧道围岩渗流场的影响。裂隙数量为10,50,100,150,200,300条。其他参数同于（1）。不同裂隙数量对隧道周围围岩水压分布影响较小。同样,取x=40的隧道中心线y=[30,50]段水压,绘制不同N值水压分布见图15。当N值越大时,隧道周围水压梯度越大。但N值变化对隧道底部围岩影响小于隧道顶部。这说明裂隙数量越多时,隧道围岩水压梯度越大,隧道流量将越大。

图 15 不同裂隙数量下隧道围岩[30, 50]段压力分布

Figure 15. Distribution of water pressure of tunnel rock at [30, 50] range under different fracture numbers

下载: 全尺寸图片幻灯片

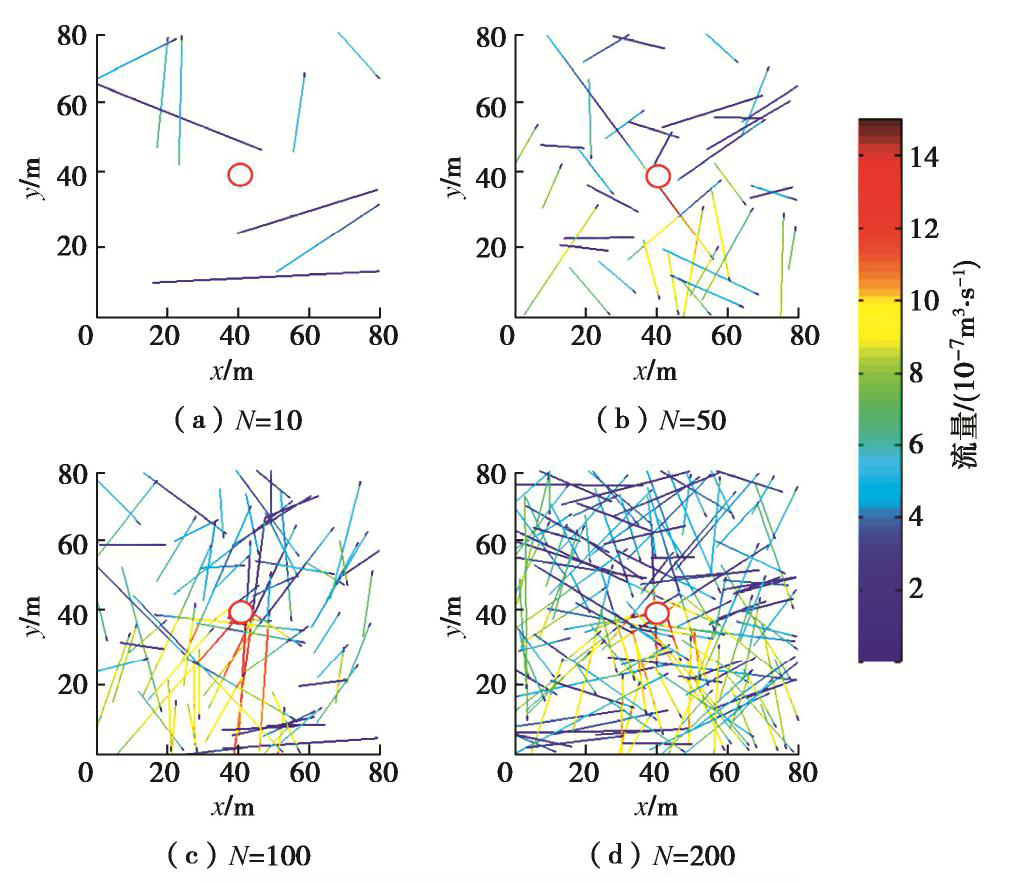
另外,计算了不同N值下裂隙网络的流量分布,如图16所示。从图中看出,N值会影响着裂隙的流量分布。N值越大时,高流量的裂隙数量越多,但主要分布于隧道附近。主要原因N值影响着裂隙的数量,N值越大,裂隙越多,越有可能与隧道相交,导致高流量的裂隙较多。

图 16 不同裂隙数量下裂隙流量分布

Figure 16. Distribution of fracture flow rate under different fracture numbers

下载: 全尺寸图片幻灯片

综上分析结果,裂隙分布均质性和密度是影响裂隙型围岩隧道的压力场和涌水量的关键因素。对于深埋富水裂隙型隧道,裂隙方向越集中于水压方向且密度越大时,隧道越容易发生涌水事故,因此要及时查明裂隙、断层等不良地质体信息,必要时采取全包防水措施。

5. 结论

本文基于有限体积法,推导了孔隙Darcy渗流和裂隙Forchheimer渗流方程的离散格式,并提出两者耦合流动的求解方法。基于该方法研究了富水深埋裂隙型围岩隧道非线性渗流规律,获得4点结论。

（1）针对单裂隙和相交裂隙算例,对比了新方法与Frih等方法结果。新方法计算得到的压力以及裂隙速度分布与Frih等和Arraras等计算结果是一致的。网格尺寸小于0.02 m和单元比率为1时,计算误差小于1%。且收敛速度较快。因此,新方法能够准确描述裂隙-孔隙双重介质非线性渗流行为。

（2）裂隙型围岩隧道围岩水压梯度呈现“底部大,顶部小”的特点,这表明,隧道底部的流量高于顶部。另外,越接近隧道位置的水力梯度越大,裂隙的流量越大。

（3）随机裂隙方向的不均匀性影响着隧道围岩的水力特性。裂隙方向越集中于水力梯度方向,围岩导水性越强,涌水量越大。

（4）裂隙密度是影响隧道围岩导水性又一重要因素。裂隙密度越大时,隧道围岩水压梯度越大,隧道流量将越大。主要原因在于裂隙密度越大,裂隙越多,越有可能与隧道相交,导致高流量的裂隙较多。

图 1 裂隙-孔隙双重介质离散示意图

Figure 1. Schematic diagram of fractured porous media

下载: 全尺寸图片幻灯片

图 2 算例1计算模型

Figure 2. Computational model for single fracture

下载: 全尺寸图片幻灯片

图 3 本文模型计算的压力分布

Figure 3. Distribution of pressure calculated by proposed method

下载: 全尺寸图片幻灯片

图 4 单裂隙模型的裂隙速度分布

Figure 4. Distribution of fracture velocity of single fracture model

下载: 全尺寸图片幻灯片

图 5 算例1网格大小与误差的关系

Figure 5. Relationship between error and mesh size

下载: 全尺寸图片幻灯片

图 6 算例1单元比率与误差的关系

Figure 6. Relationship between error and element ratio

下载: 全尺寸图片幻灯片

图 7 相交裂隙计算模型

Figure 7. Computational model for intersecting fracture

下载: 全尺寸图片幻灯片

图 8 相交裂隙1新方法计算的压力

Figure 8. Distribution of pressure calculated by proposed method for intersecting fracture case 1

下载: 全尺寸图片幻灯片

图 9 相交裂隙2新方法计算的压力

Figure 9. Distribution of pressure calculated by proposed method for intersecting fracture case 2

下载: 全尺寸图片幻灯片

图 10 相交裂隙网格大小与误差的关系

Figure 10. Relationship between error and mesh size for intersecting fracture model

下载: 全尺寸图片幻灯片

图 11 相交裂隙单元比率与误差的关系

Figure 11. Relationshp between error and mesh ratio for intersecting fracture model

下载: 全尺寸图片幻灯片

图 12 隧道模型尺寸及边界条件

Figure 12. Dimension and boundary of tunnel model

下载: 全尺寸图片幻灯片

图 13 不同κ值下隧道围岩[30, 50]段压力分布

Figure 13. Distribution of water pressure of tunnel rock at [30, 50] range under different values of κ

下载: 全尺寸图片幻灯片

图 14 不同κ值下裂隙流量分布

Figure 14. Distribution of fracture flow rate under different values of κ

下载: 全尺寸图片幻灯片

图 15 不同裂隙数量下隧道围岩[30, 50]段压力分布

Figure 15. Distribution of water pressure of tunnel rock at [30, 50] range under different fracture numbers

下载: 全尺寸图片幻灯片

图 16 不同裂隙数量下裂隙流量分布

Figure 16. Distribution of fracture flow rate under different fracture numbers

下载: 全尺寸图片幻灯片

表 1 裂隙几何参数

Table 1 Geometrical parameters of fractures

长度/m 开度/mm 倾角数量N
l_min l_max λ b μ κ

1.0 60.0 1.0 0.1 50° [0,8] [10,300]

下载: 导出CSV

参考文献(23)

[1]	LEI Q H, LATHAM J P, TSANG C F. The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks[J]. Computers and Geotechnics, 2017, 85: 151-176. doi: 10.1016/j.compgeo.2016.12.024
[2]	毛昶熙, 陈平, 李祖贻, 等. 裂隙岩体渗流计算方法研究[J]. 岩土工程学报, 1991, 13(6): 1-10. doi: 10.3321/j.issn:1000-4548.1991.06.001 MAO Chang-xi, CHEN Ping, LI Zu-yi, et al. Study on computation methods of seepage flow in fractured rock masses[J]. Chinese Journal of Geotechnical Engineering, 1991, 13(6): 1-10. (in Chinese) doi: 10.3321/j.issn:1000-4548.1991.06.001
[3]	张有天. 从岩石水力学观点看几个重大工程事故[J]. 水利学报, 2003, 34(5): 1-10. doi: 10.3321/j.issn:0559-9350.2003.05.001 ZHANG You-tian. Analysis on several catastrophic failures of hydraulic projects in view of rock hydraulics[J]. Journal of Hydraulic Engineering, 2003, 34(5): 1-10. (in Chinese) doi: 10.3321/j.issn:0559-9350.2003.05.001
[4]	周志芳, 王锦国. 裂隙介质水动力学[M]. 北京: 中国水利水电出版社, 2004. ZHOU Zhi-fang, WANG Jin-guo. Theory of Dynamics of Fluids in Fractured Media[M]. 2004. (in Chinese)
[5]	HUYAKORN P S, LESTER B H, FAUST C R. Finite element techniques for modeling groundwater flow in fractured aquifers[J]. Water Resources Research, 1983, 19(4): 1019-1035. doi: 10.1029/WR019i004p01019
[6]	ATHANI S S, SHIVAMANTH , SOLANKI C H, et al. Seepage and stability analyses of earth dam using finite element method[J]. Aquatic Procedia, 2015, 4: 876-883. doi: 10.1016/j.aqpro.2015.02.110
[7]	MARYŠKA J, SEVERÝN O, VOHRALÍK M. Numerical simulation of fracture flow with a mixed-hybrid FEM stochastic discrete fracture network model[J]. Computational Geosciences, 2005, 8(3): 217-234. doi: 10.1007/s10596-005-0152-3
[8]	王恩志. 岩体裂隙的网络分析及渗流模型[J]. 岩石力学与工程学报, 1993, 12(3): 214-221. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX199303002.htm WANG En-zhi. Network analysis and seepage flow model of fractured rockmass[J]. Chinese Journal of Rock Mechanics and Engineering, 1993, 12(3): 214-221. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX199303002.htm
[9]	何杨, 柴军瑞, 唐志立, 等. 三维裂隙网络非稳定渗流数值分析[J]. 水动力学研究与进展A辑, 2007, 22(3): 338-344. doi: 10.3969/j.issn.1000-4874.2007.03.011 HE Yang, CHAI Jun-rui, TANG Zhi-li, et al. Numerical analysis of 3-D unsteady seepage through fracture network in rock mass[J]. Journal of Hydrodynamics (SerA), 2007, 22(3): 338-344. (in Chinese) doi: 10.3969/j.issn.1000-4874.2007.03.011
[10]	李海枫, 张国新, 朱银邦. 裂隙岩体三维渗流网络搜索及稳定渗流场分析[J]. 岩石力学与工程学报, 2010, 29(增刊2): 3447-3454. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S2004.htm LI Hai-feng, ZHANG Guo-xin, ZHU Yin-bang. Three-dimensional seepage network searching of fractured rock mass and steady seepage field analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3447-3454. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S2004.htm
[11]	ZIMMERMAN R W, HADGU T, BODVARSSON G S. A new lumped-parameter model for flow in unsaturated dual-porosity media[J]. Advances in Water Resources, 1996, 19(5): 317-327. doi: 10.1016/0309-1708(96)00007-3
[12]	PERATTA A, POPOV V. A new scheme for numerical modelling of flow and transport processes in 3D fractured porous media[J]. Advances in Water Resources, 2006, 29(1): 42-61. doi: 10.1016/j.advwatres.2005.05.004
[13]	张奇华, 徐威, 殷佳霞. 二维任意裂隙网络裂隙-孔隙渗流模型的两种解法[J]. 岩石力学与工程学报, 2012, 31(2): 217-227. doi: 10.3969/j.issn.1000-6915.2012.02.001 ZHANG Qi-hua, XU Wei, YIN Jia-xia. Two-dimensional fractured porous flow model of arbitrary fracture network and its two solution methods[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(2): 217-227. (in Chinese) doi: 10.3969/j.issn.1000-6915.2012.02.001
[14]	阙云, 熊汉, 刘慧芬, 等. 基于非饱和大孔隙流双重介质模型的浸水边坡水力响应数值模拟[J]. 工程科学与技术, 2020, 52(6): 102-110. https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH202006012.htm QUE Yun, XIONG Han, LIU Hui-fen, et al. Numerical simulation of hydraulic response of immersed slope based on dual-permeability model of unsaturated macropore flow[J]. Advanced Engineering Sciences, 2020, 52(6): 102-110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SCLH202006012.htm
[15]	宋晓晨, 徐卫亚. 非饱和带裂隙岩体渗流的特点和概念模型[J]. 岩土力学, 2004, 25(3): 407-411. doi: 10.3969/j.issn.1000-7598.2004.03.016 SONG Xiao-chen, XU Wei-ya. Features and conceptual models of flow in fractured vadose zone[J]. Rock and Soil Mechanics, 2004, 25(3): 407-411. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.03.016
[16]	LANG P S, PALUSZNY A, ZIMMERMAN R W. Permeability tensor of three-dimensional fractured porous rock and a comparison to trace map predictions[J]. Journal of Geophysical Research: Solid Earth, 2014, 119(8): 6288-6307. doi: 10.1002/2014JB011027
[17]	蒋中明, 肖喆臻, 唐栋. 坝基岩体裂隙渗流效应数值模拟方法[J]. 水利学报, 2020, 51(10): 1289-1298. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202010011.htm JIANG Zhong-ming, XIAO Zhe-zhen, TANG Dong. Numerical analysis method of fluid flow in fractured rock mass of dam foundation[J]. Journal of Hydraulic Engineering, 2020, 51(10): 1289-1298. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202010011.htm
[18]	FRIH N, ROBERTS J E, SAADA A. Modeling fractures as interfaces: a model for Forchheimer fractures[J]. Computational Geosciences, 2008, 12(1): 91-104. doi: 10.1007/s10596-007-9062-x
[19]	ARRARÁS A, GASPAR F J, PORTERO L, et al. Geometric multigrid methods for Darcy-Forchheimer flow in fractured porous media[J]. Computers & Mathematics With Applications, 2019, 78(9): 3139-3151.
[20]	姚池, 邵玉龙, 杨建华, 等. 非线性渗流对裂隙岩体渗流传热过程的影响[J]. 岩土工程学报, 2020, 42(6): 1050-1058. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006011.htm YAO Chi, SHAO Yu-long, YANG Jian-hua, et al. Effect of nonlinear seepage on flow and heat transfer process of fractured rocks[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 1050-1058. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006011.htm
[21]	HAJIBEYGI H, KARVOUNIS D, JENNY P. A hierarchical fracture model for the iterative multiscale finite volume method[J]. Journal of Computational Physics, 2011, 230(24): 8729-8743.
[22]	XIONG F, WEI W, XU C S, et al. Experimental and numerical investigation on nonlinear flow behaviour through three dimensional fracture intersections and fracture networks[J]. Computers and Geotechnics, 2020, 121: 103446.
[23]	KARIMI-FARD M, DURLOFSKY L J, AZIZ K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators[J]. SPE Journal, 2004, 9(2): 227-236.

施引文献(24)

期刊类型引用(10)

1.	宁佳祺，冯子军，高祺. 裂隙-孔隙双重介质模型下的复杂裂隙岩体示踪传质特性. 科学技术与工程. 2025(07): 2904-2913 . 百度学术
2.	朱寅斌，李长冬，周佳庆，项林语，姜茜慧，朱文宇. 考虑基质渗透性的粗糙单裂隙非达西流动特性研究. 岩土力学. 2024(02): 601-611 . 百度学术
3.	雷海林，张万栋，张汉康. 基于有限元方法的水利工程坝体稳定性监测研究. 水利科技与经济. 2024(03): 152-157 . 百度学术
4.	冀超辉. 我国煤层瓦斯运移模型研究进展. 煤矿安全. 2024(06): 8-18 . 百度学术
5.	谢福星. 地面充填钻孔钻进过程应力-位移演化规律数值模拟研究. 建井技术. 2024(04): 1-6 . 百度学术
6.	许增光，李煜婷，曹成. 岩土体介质非达西渗流特性研究进展. 应用力学学报. 2024(06): 1211-1236 . 百度学术
7.	卢玉东，国金琦，程大伟，毛兴隆. 考虑固液二相互态特性的流固耦合模型. 中国公路学报. 2023(01): 58-69 . 百度学术
8.	代盟，刘志帆，张启勇. 基于双重介质模型的正仲氢转化器流动规律研究. 低温与超导. 2023(04): 33-39 . 百度学术
9.	赵辉，李伯英，周玉辉，张琪，刘洪发，王文才，王晓龙. 基于高速非达西渗流的断溶体油藏连通性预测模型. 石油学报. 2022(07): 1026-1034 . 百度学术
10.	李博，王晔，邹良超，杨磊. 岩石裂隙内浆液–水两相流可视化试验与驱替规律研究. 岩土工程学报. 2022(09): 1608-1616+2-3 . 本站查看