Centrifuge test on single pile with different rigidities in saturated clay under cyclic lateral loading
-
摘要: 对正常固结黏土中具有不同桩土相对刚度单桩基础的水平静力及循环承载特性开展离心试验研究。在相同土层及桩基埋深条件下,通过调整模型桩材料及桩身截面几何尺寸,实现桩土相对刚度调节,对比组包括刚性桩、柔性桩和半刚性桩。在加载试验前执行T-bar循环插拔试验,各组试验土体强度与弱化参数一致,验证了制样的可靠性。桩基归一化荷载–位移曲线初始刚度和归一化极限承载力均随桩土相对刚度系数增大而增大,表明桩土相对刚度系数可用于描述水平受荷桩静力承载特性。尽管刚性桩刚度受循环荷载的影响更大,其循环稳定桩侧刚度仍显著优于柔性桩结果。循环稳定桩侧刚度与静力刚度比值随桩土相对刚度增大而减低,从长期刚度控制的角度,不断增大桩径不利于长期稳定承载,可通过增大桩基埋深提升长期承载的稳定性。Abstract: The centrifuge tests are carried out to investigate the static and cyclic lateral bearing behaviors of single pile with different pile-soil relative rigidities in normal consolidated clay. Under the same soil and pile-buried depth condition, the pile-soil relative rigidity is tuned by adjusting the model pile material and the section geometric parameter. The comparison group includes rigid pile, flexible pile and semi-rigid pile. Before the loading tests, the cyclic T-bar tests are performed, with the results indicating that the clay strength profile and softening parameter of each test are consistent, verifying the reliability of sample preparation. Both the initial stiffness and the ultimate bearing capacity of the normalized load-displacement curve of piles increase with the increase of pile-soil relative rigidity factor, which indicates that the pile-soil relative rigidity factor can be used to describe the static bearing behavior of the laterally loaded pile. Although the rigid pile is more affected under cyclic loading, its cyclic stable stiffness is still significantly larger than that of a flexible pile. The ratio of cyclic stable stiffness to static stiffness decreases under the increasing pile-soil relative rigidity factor. From the perspective of long-term stiffness control, increasing the pile diameter is not conducive to stable performance, which can be improved by increasing the pile-buried depth.
-
Keywords:
- saturated clay /
- laterally loaded pile /
- cyclic loading /
- pile-soil relative rigidity
-
0. 引言
在海洋工程中,桩基础除了承担上部结构自重及恒载外,还将受到交通、波浪以及风力等具有明显周期性的水平向循环荷载作用,致使其在长期服役过程中产生承载力弱化和累积变形,并可能影响上部结构的正常使用。桩基础在海洋环境中的主要应用形式可分为：①群桩基础（单桩桩径D为0.5～2.0 m,长径比L/D为40～100）,②单桩基础（桩径D为2.0～8.0 m,长径比L/D为4～10）,二者之间差异显著,前者多用于传统海上石油平台,后者则是海上风电设备的主要基础选型。
Poulos等[1]基于弹性分析结果发现桩基水平承载特性与桩身几何尺寸、材料及桩周土体特性密切相关,并提出桩土相对刚度系数KR=(EpIp)/EsL4,其中Ep为桩身弹性模量,Ip为桩身截面抗弯刚度,Es为土体模量,L为桩基埋深,当KR>0.208时为刚性桩,当KR<2.5×10-3时则为柔性桩。20世纪70年代美国石油协会API[2]资助了包括水平受荷桩静力和循环加载的系列原位试验研究[3-4],并基于试验结果总结了黏土和砂土中水平受荷单桩在静力和长期循环荷载下的非线性p–y曲线形式,其中循环加载的影响通过对静力极限承载力打折进行考虑。由于API规范所基于的试验试桩均为小直径柔性柱（D=0.152～0.609 m）,已有研究[5-7]表明其不适于用大直径单桩基础设计。
在桩基水平循环承载特性方面,Zhang等[8]展开了饱和黏土中刚性短桩循环弱化特性的研究,其通过T-bar[9]循环插拔试验标定土体不排水强度弱化参数,并首次建立了桩侧刚度循环弱化规律与土体塑性累积位移之间的关系。Hong等[10]对饱和黏土中半刚性桩的水平循环承载特性进行离心试验研究,发现随桩侧土体弱化,桩基承载模式逐渐趋于刚性整体转动,并基于桩周土体孔压随循环加载演化结果揭示黏土不排水强度弱化真实机理。Yu等[11]对正常固结黏土中的大直径桩水平静力及循环加载特性进行了离心试验研究,其在循环试验中分进行了采用力与位移两种控制模式,并基于T-bar循环插拔试验结果建立了桩侧承载力弱化规律与土体累积塑性应变之间的关系。
综上,桩土相对刚度系数与桩基静力承载特性影响的研究已较为完善,而循环加载试验研究仅针对一根桩展开,难以全面评价桩土相对刚度对桩基循环承载特性的影响。俞剑等[12]分别针对柔性桩和刚性桩开展的循环加载试验研究,但其仅包括2根模型桩,且1g物理模型试验自身具有无法有效地复现土体实际应力状态的缺陷。因此,本研究对具有相同埋深和不同桩身抗弯刚度的3根模型桩进行循环加载离心试验研究,并控制试验条件与Yu等[11]一致,以形成4组具有不同桩土相对刚度的对比组。
1. 离心模型试验设备
1.1 加载装置
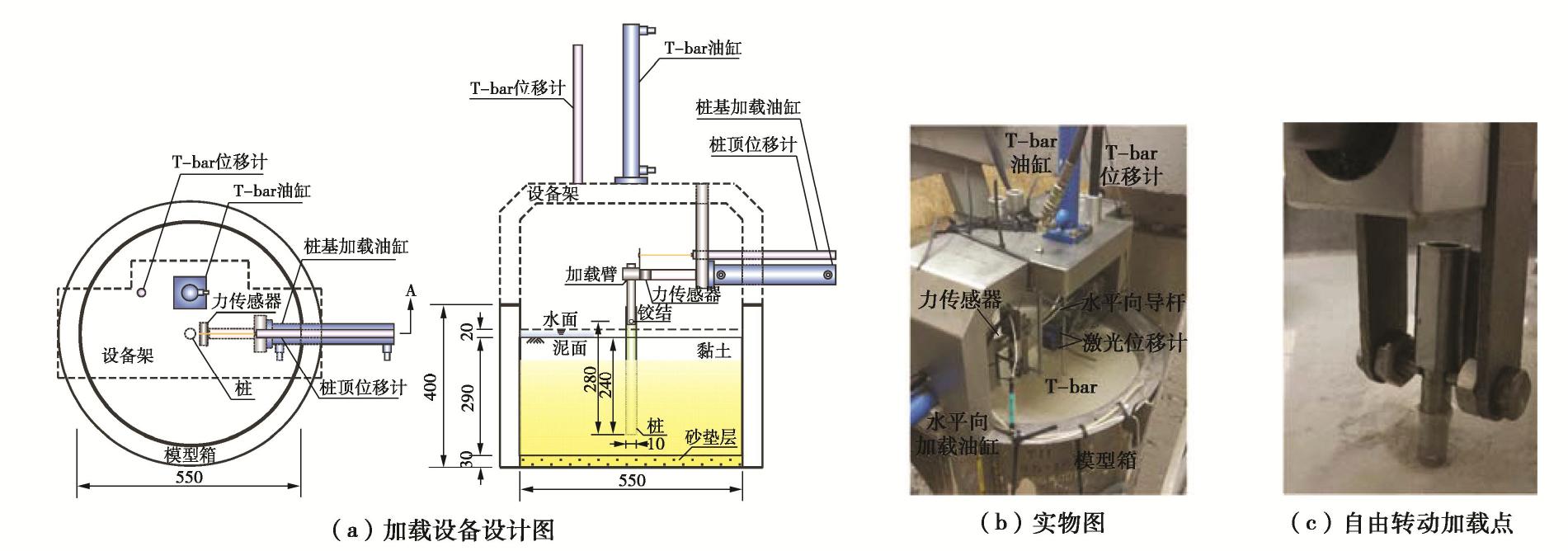
本次试验均采用新加坡国立大学梁式离心机完成,它有效半径为2 m,最大载重能力为40 g·t,本次所有试验均在50g加速度下完成。模型箱为圆柱形,采用不锈钢制成,其内径为550 mm,深度为400 mm,在反力架上设置水平和竖向两套伺服控制加载系统分别用于控制桩基加载和T-bar贯入试验,如图1所示。通过穿过桩基加载点处预留钻孔的钨钢轴承杆,将桩顶与金属加载块铰接,从而实现对桩顶施加水平荷载时允许桩顶自由转动。土样采用正常固结黏土,通过改变桩身截面参数及桩基埋深来调整桩–土相对刚度。
1.2 模型桩
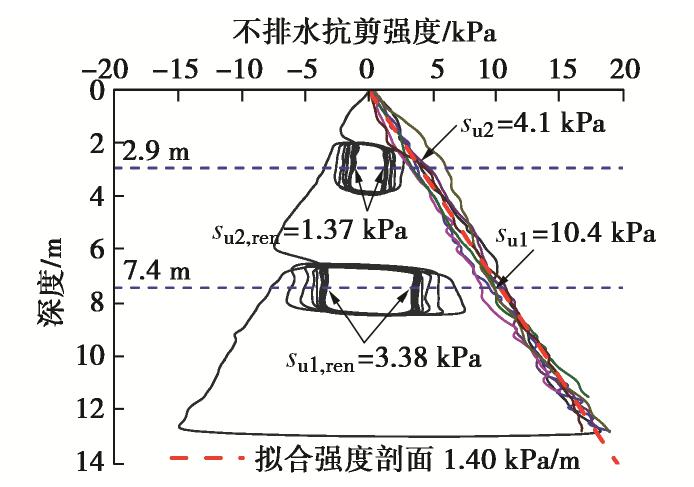
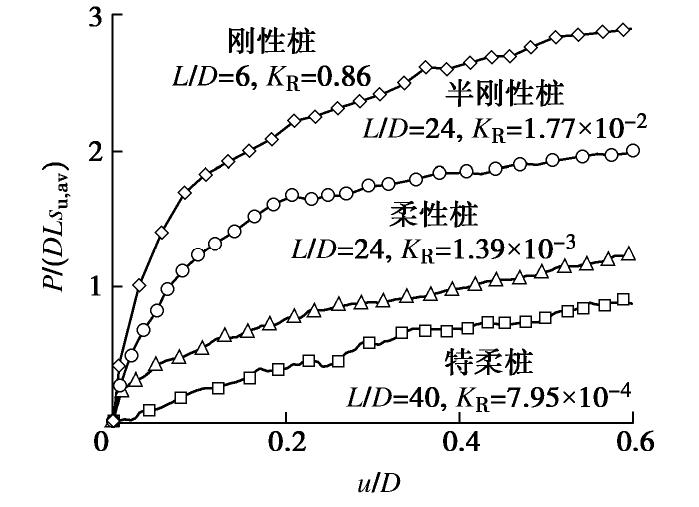
为了研究不同桩–土相对刚度对单桩水平循环承载特性的影响,分别对特柔桩、柔性桩、半刚性桩（根据桩土相对刚度系数[1]命名）开展了离心试验。表1列出了每根模型桩的几何参数、截面特性、土体力学参数及桩–土相对刚度系数（原型参数）,并与刚性桩[11]对比,λ为土体不排水强度剖面斜率,Es基于不排水抗剪强度估算[13]。
表 1 桩基参数Table 1. Parameters of piles模型桩 L/m D/m Ip/m4 Ep/GPa λ/(kPa·m-1) Es/kPa KR 特柔桩 12 0.3 6.28×10-11 70 1.40 1668 7.95×10-4 柔性桩 12 0.5 1.10×10-10 70 1.40 1668 1.39×10-3 半刚性桩 12 0.5 4.91×10-10 200 1.40 1668 1.77×10-2 刚性桩[11] 12 2.0 2.4×10-8 200 1.39 1668 0.86 1.3 土样制备
正常固结饱和黏土样制备过程与Yu等[11]完全一致,简述如下。按含水率120%确定高岭土干粉与水配比,进行6 h真空搅拌,得到饱和泥浆。饱和泥浆固结沉降较大,为保证完成固结后的土层厚度满足试验要求,采用套筒加高模型箱。在1g条件下通过逐级增加砝码进行预压固结,最终预固结压力为4 kPa。预压过程中通过排水管引流形成稳定回流,避免固结排水造成顶部土体不饱和。预压时间由土样顶面压缩沉降控制,当土样顶面低于模型箱上缘15 mm左右时,预压固结结束,取下套筒,整个预压固结周期约为7 d。将完成预压固结的土样置于50g离心场中进行初次固结,在土面沉降稳定后停机并进行压桩。
2. 试验方案及试验过程
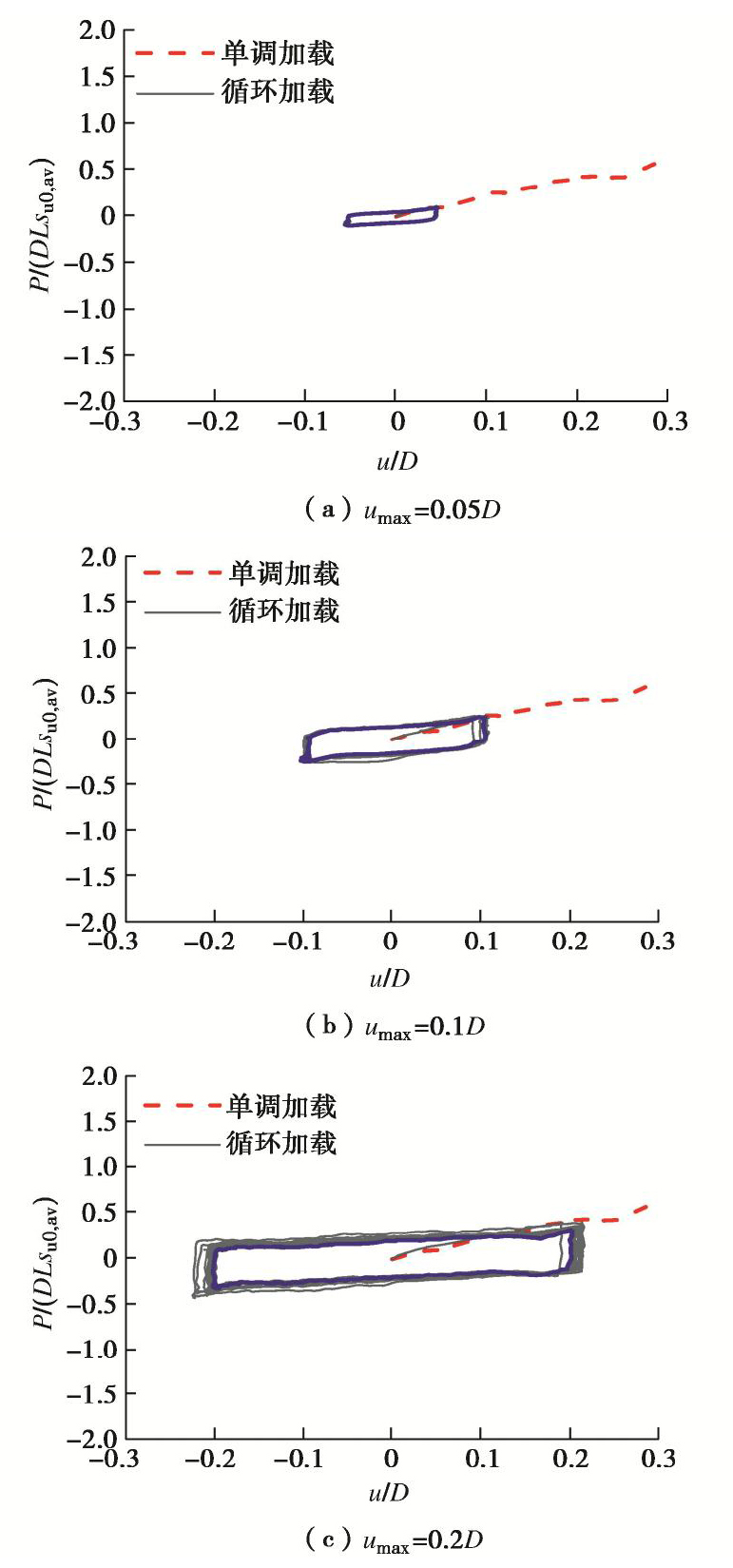
对每根模型桩均进行单调加载试验及位移控制双向循环加载试验,循环加载位移幅值umax分别采用0.05D,0.1D及0.2D,从而全面研究桩土相对刚度和循环幅值对单桩水平承载力弱化趋势的影响。
Craig[14]与Ilyas等[15]的离心试验研究表明,在1g或离心场中压桩,对于桩基水平承载特性没有明显影响,因此本次试验采用1g压桩方案。土样在离心场中经过第一次固结后停机,在模型箱上安装加载设备,并利用伺服系统在1g情况下以1 mm/s的速率将模型桩压入土中。压桩完毕后,将T-bar固定至竖向油缸。测量元件安装结束后,重启离心机,并在50g下固结10 h,以消除压桩对土体产生的轻微扰动。二次固结完成后,在离心条件（50g）下通过T-bar循环贯入试验测定土体不排水抗剪强度及循环弱化参数。为保证在T-bar插拔及桩基加载过程中土体处于不排水状态,需满足Finnie[16]提出的不排水状态判定公式：
vDT-barcv>30, (1) 式中,DT-bar（5 mm）为T-bar直径,v为运行速率,cv为固结系数（cv=4.76×10-3 cm2/s）。根据式（1）,3 mm/s已满足土体不排水状态,因此T-bar循环插拔及桩基加载速率均采用3 mm/s。
3. 试验结果及分析
3.1 T-bar试验结果
图2显示了通过实测T-bar净抗力q确定的土体不排水抗剪强度su=q/Np,Np =10.5为T-bar（粗糙系数α=0.34的圆桩）截面对应的极限承载力系数[17]。初次贯入确定的不排水抗剪强度剖面平均斜率λ约为1.40 kPa/m,验证了本试验所制备的土样性质基本一致,并与Yu等[11]的土样条件基本吻合（λ=1.39 kPa/m）。
若不考虑应变率对强度的影响,则饱和黏土不排水抗剪强度随累积塑性应变的弱化公式[18]如下：
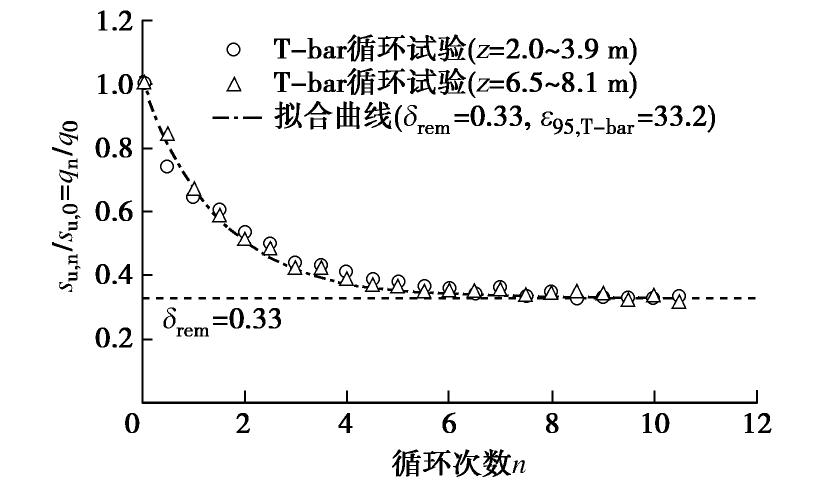
su=su0[δrem+(1−δrem)exp(−3εε95)]。 (2) 式中 su0为初次加载对应的不排水抗剪强度初始值；δrem为残余强度占初始强度的比例；ε95是引起土体可弱化部分的强度到达95%弱化所需的累积塑性剪应变；ε为累积塑性剪应变。
Einav等[18]还提出了一套根据T-bar试验结果确定弱化模型参数的方法：
su,n=qnNp=su0[δrem+(1−δrem)exp(−32nεT-barε95,T-bar)]。 (3) 式中 n为T-bar循环次数,一次拔取与贯入为1个完整的循环；qn为第n次循环对应的T-bar净抗力；su,n为与qn相对应的弱化后不排水抗剪强度；εT-bar（εT-bar=3.7[19]）为T-bar一次拔取或贯入土体中的平均累积塑性剪应变。图3显示了根据式（3）对本次T-bar循环试验处理后的结果。图3表明对正常固结黏土地基,不排水强度比su,n/su0随循环次数n的弱化规律受深度影响不大,可采用一套弱化模型参数对其进行描述。通过拟合得到土体循环弱化参数δrem=0.33,ε95,T-bar=33.2。
3.2 静力加载试验结果
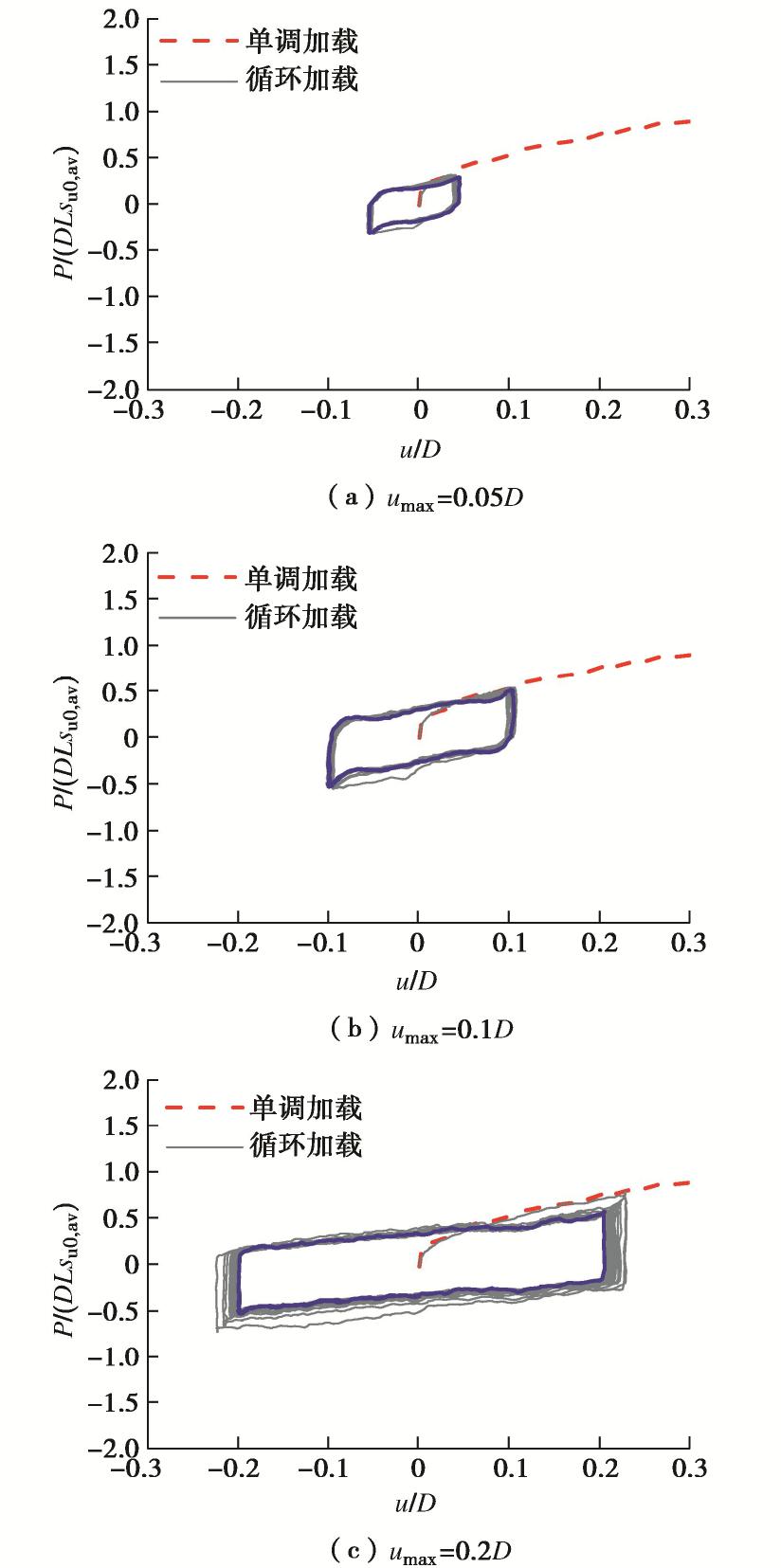
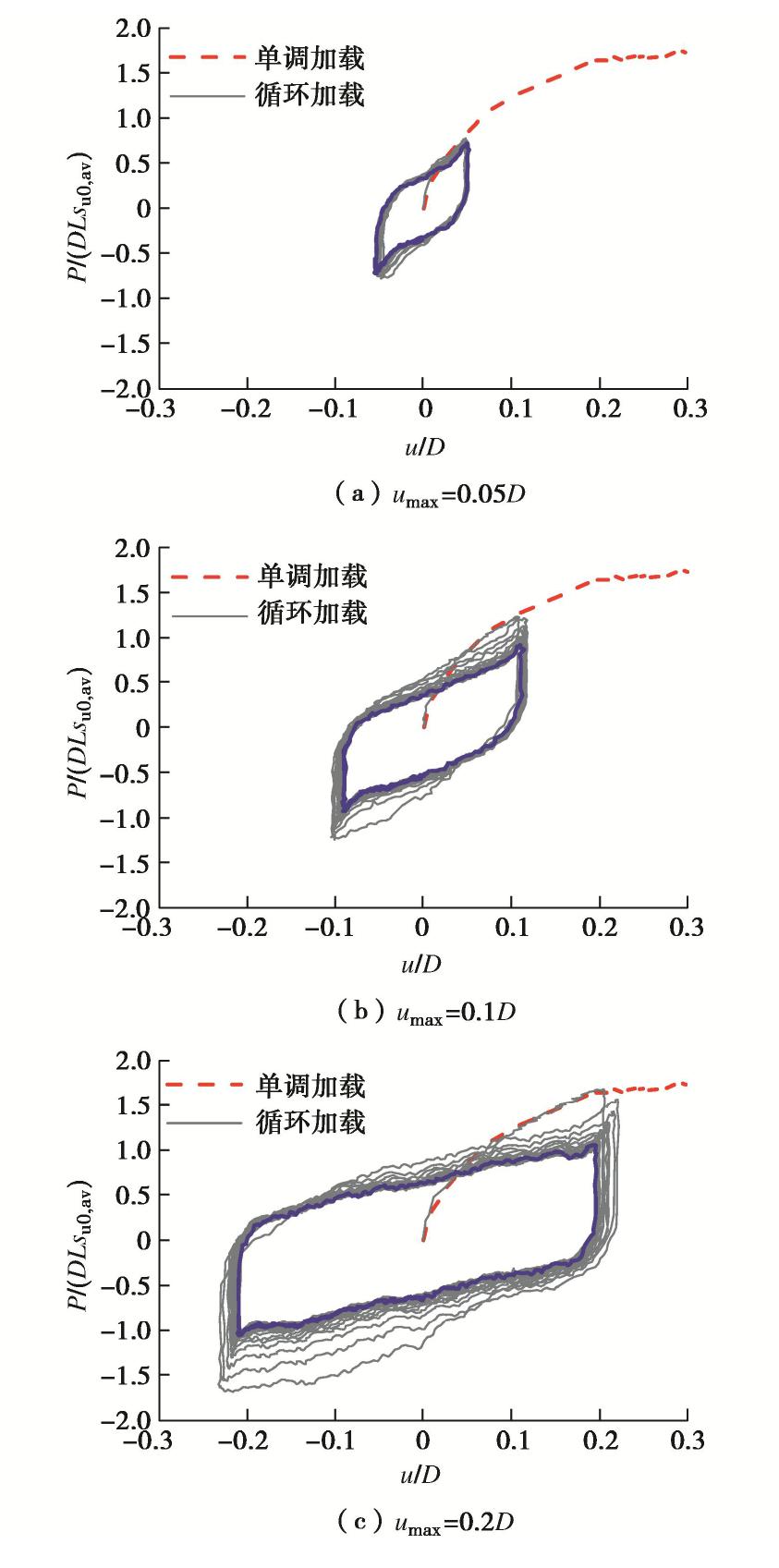
静力加载试验通过位移加载控制,最大加载位移为0.6D。图4显示了本次试验的特柔桩、柔性桩、半刚性桩在桩顶自由加载条件下的静力响应,并与相同土样及加载条件下的刚性桩[11]试验结果进行对比。为方便对比,分别采用DLsu,av和D对荷载和位移进行归一化,其中桩基埋深范围内土体的不排水强度平均值su,av=∫su(z)dz/L。上述4根桩基具有相同的埋深及土样条件,因此其初始承载特性差异主要由桩身截面特性变化所导致,而桩身截面特性差异可以通过桩土相对刚度KR来描述。KR越大,实测桩基荷载–位移曲线初始段斜率越大,与试验设计相吻合。
图4中荷载–位移曲线斜率随位移增大逐渐降低,表明桩–土承载系统已进入弹塑性阶段。理论上,采用弹性参数定义的KR仅能反映桩–土系统初始弹性状态,而无法反映其弹塑性状态,但图5中桩基在弹塑性承载阶段获得的归一化荷载Pult/(DLsu,av)也随KR增大而增大。从桩–土承载模式的角度,随着KR增大桩身变形逐渐由桩身挠曲为主转为刚性转动为主,迫使深部强度较大的土体参与抵抗外力,从而使归一化荷载结果增大。综上,可以采用参数KR近似描述桩基截面特性改变引起的桩–土静力承载特性差异。
3.3 循环加载试验结果
图5～7分别显示了不同桩基的水平循环加试验结果。桩顶荷载–位移滞回曲线结果在初次加载时与静力试验结果重合,随着循环次数n增加桩顶荷载逐渐弱化导致滞回圈高度减小,并最终趋于稳定。对一根桩,稳定滞回圈横边斜率随umax增大逐渐减小,稳定滞回曲线趋于扁平。结合静力结果可知随着umax增大,稳定荷载偏离静力结果的程度逐渐增大,与土体强度弱化随累积塑性应变水平增大的假设一致。
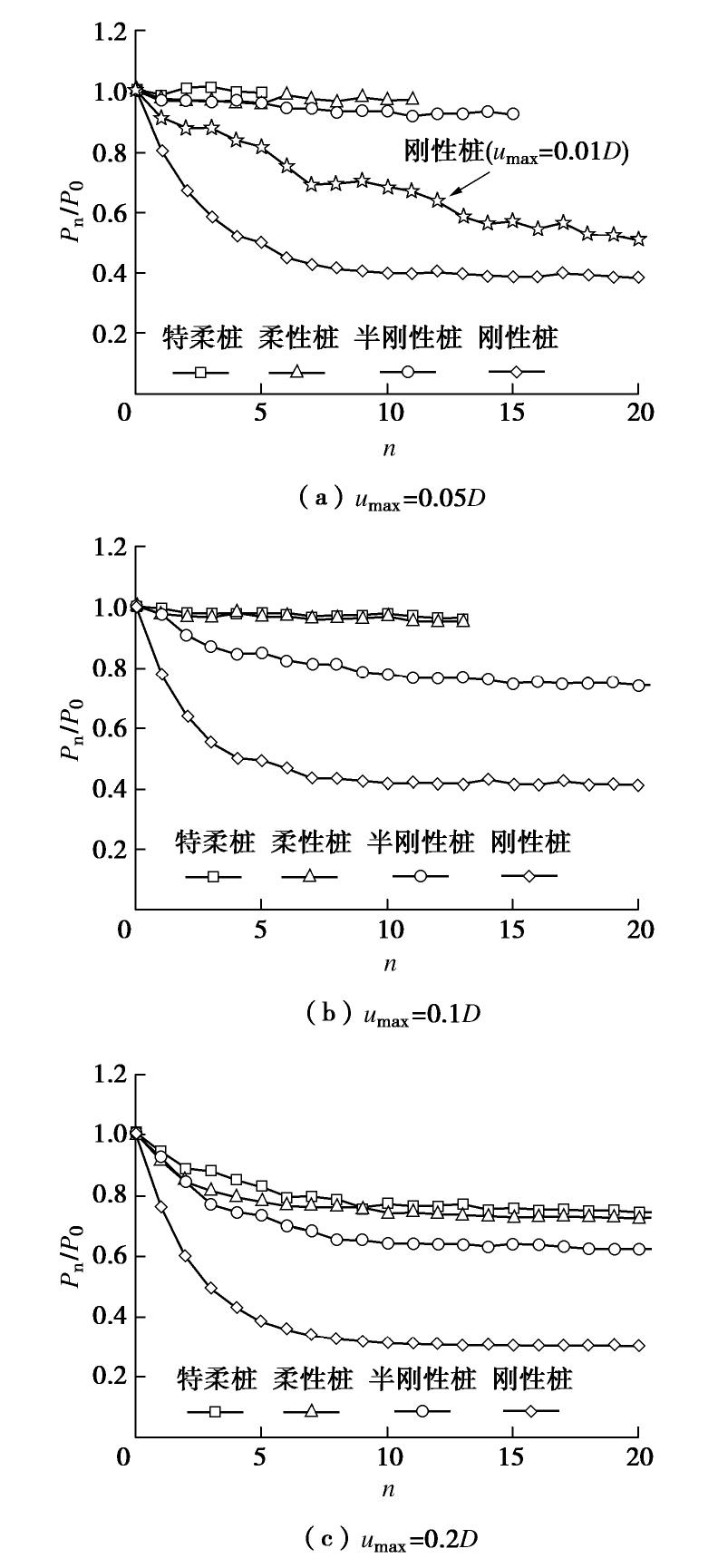
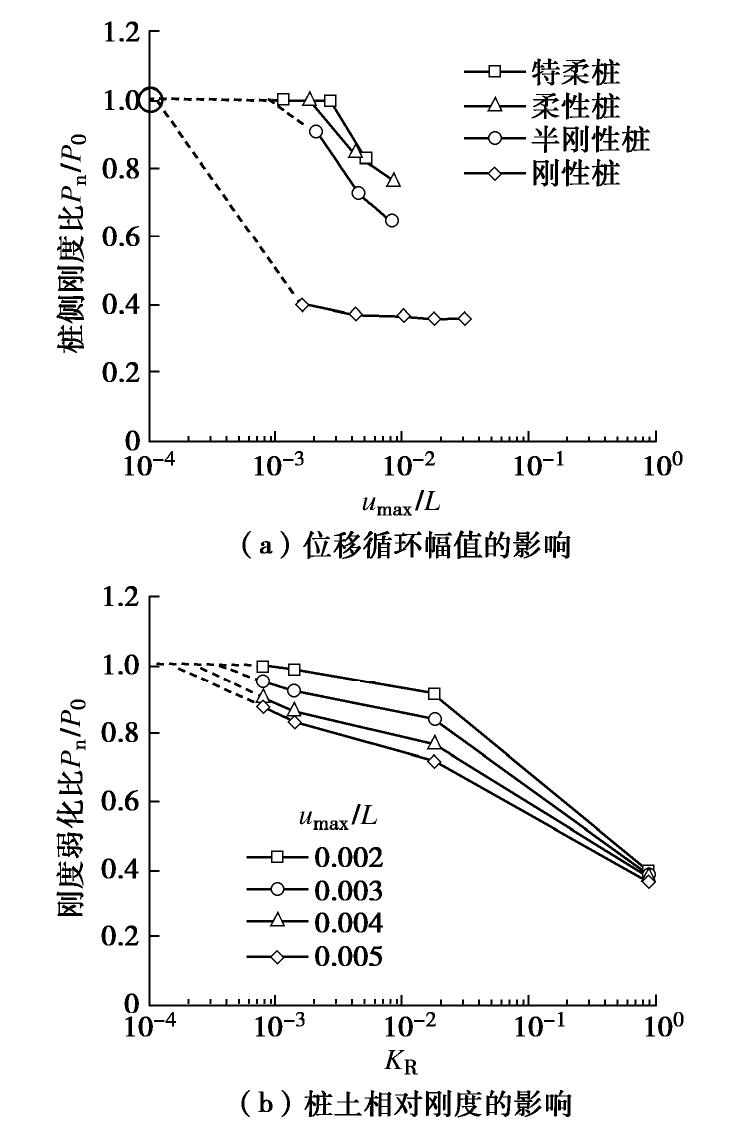
图8表明桩基础的荷载比Pn/P0弱化量随KR增大而增大,Pn/P0=[Pn/(su0,avumaxL)]/[P0/(su0,avumaxL)]也可以作为归一化桩侧刚度比。当umax=0.05D时,特柔桩与柔性桩的Pn/P0弱化非常缓慢；半刚性桩发生轻微弱化,循环稳定的Pn/P0约为92%；刚性桩则发生显著弱化,循环稳定的Pn/P0约为40%。当umax=0.1D时,特柔桩与柔性桩的Pn/P0弱化仍非常缓慢；半刚性桩与刚性桩则呈现显著弱化,其循环稳定的Pn/P0分别约为70%和40%。当umax=0.2D时,所有桩基的Pn/P0均显著弱化。刚性桩在umax=0.05D～0.2D下的Pn/P0弱化规律相近。为此,补充umax=0.01D循环加载试验,其Pn/P0弱化速率显著慢于umax≥0.05D的结果,表明对刚性桩（D=2 m）,0.05D位移循环幅值已较大。综上,桩侧刚度比弱化速率分别随KR和umax增大而增大,桩基达到稳定承载状态的循环次数分别与KR和umax成反比关系。
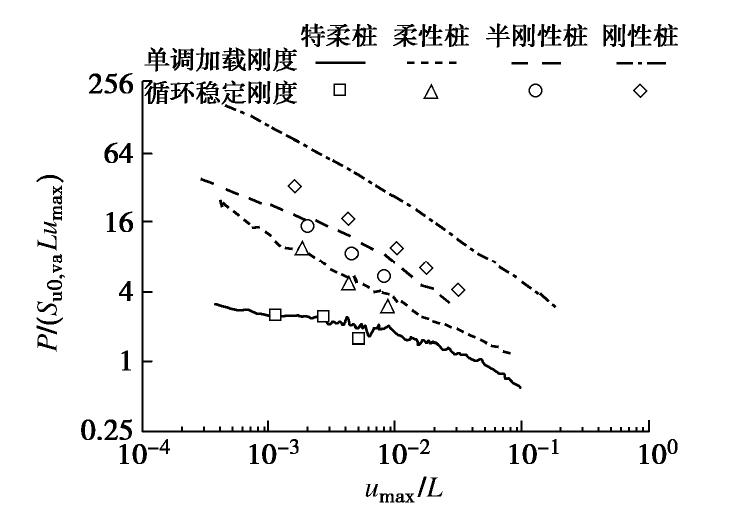
图9显示了4根桩基的桩侧静力刚度及循环稳定值P/(su0,avumaxL)。随着umax/L增大,循环稳定桩侧刚度与静力刚度均衰减,且二者之间的差异逐渐扩大。在相同umax/L水平下,尽管KR较大桩基刚度受循环荷载的影响更大,其循环稳定桩侧刚度仍显著优于柔性桩结果。
图10分别显示了umax/L和KR对循环稳定桩侧刚度与静力刚度之比Pn/P0的影响,若umax/L足够小,Pn/P0趋于1,随着umax/L增大,Pn/P0逐渐减小,如图10（a）所示；若KR足够小,Pn/P0趋于1,随着KR增大,Pn/P0逐渐减小,如图10（b）所示。从桩基长期服役性能的角度,桩侧刚度保持稳定有利于其动力承载特性。在保持桩基埋深不变条件下,虽然通过扩大桩径的方式可以有效提升静力刚度和承载力,但后期使用性能弱化程度也较为严重。在静力承载力和循环稳定桩侧刚度能满足使用要求的情况下,可以考虑采取增大桩基埋深而非桩径的方案,从而提升其长期承载的稳定性。
4. 结论与建议
本文对正常固结饱和黏土中单桩的水平循环承载特性展开离心试验研究,探索了桩土相对刚度对桩基水平循环承载特性的影响。
（1）单调加载试验结果表明桩土相对刚度系数可以较好地反应水平受荷桩的静力承载特性,桩基归一化荷载–位移曲线初始刚度和归一化极限承载力均随桩土相对刚度系数增大而增大。
（2）随位移循环幅值增大,循环稳定桩侧刚度逐渐衰减,且其与静力刚度之间的差异逐渐扩大。尽管刚性桩刚度受循环荷载的影响更大,其循环稳定桩侧刚度仍显著优于柔性桩结果。
（3）尽管增大桩土相对刚度系数可有效提升静力承载力,循环稳定桩侧刚度与静力刚度之比相应降低。从长期刚度控制的角度,在固定荷载条件下,不断增大桩径（桩身抗弯刚度）不利于长期稳定承载,可通过增大桩基埋深提升长期承载的稳定性。
-
[1] POULOS H G, DAVIS E H. Pile Foundation Analysis and Design[M]. New York: Wiley, 1980.
[2] American Petroleum Institute. Recommended Practice For Planning, Designing and Constructing Fixed Offshore Platforms[S]. 1987.
[3] MATLOCK H. Correlations for design of laterally loaded piles in soft clay[C]//Proceedings of the 2nd Offshore Technology Conference, 1970, Houston.
[4] REESE L C, WELCH R C. Lateral loading of deep foundations in stiff clay[J]. Journal of the Geotechnical Engineering Division, ASCE, 1975, 101(7): 633-650. doi: 10.1061/AJGEB6.0000177
[5] TAK KIM B, KIM N K, JIN Lee W, et al. Experimental load-transfer curves of laterally loaded piles in Nak-Dong River sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(4): 416-425. doi: 10.1061/(ASCE)1090-0241(2004)130:4(416)
[6] 朱斌, 熊根, 刘晋超, 等. 砂土中大直径单桩水平受荷离心模型试验[J]. 岩土工程学报, 2013, 35(10): 1807-1815. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201310007.htm ZHU Bin, XIONG Gen, LIU Jin-chao, et al. Centrifuge modelling of a large-diameter single pile under lateral loads in sand[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1807-1815. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201310007.htm
[7] BYRNE B, MCADAM R, BURD H, et al. PISA: new design methods for large diameter piles under lateral loading for offshore wind applications[C]//Proceedings of the 3rd International Symposium on Frontiers in Offshore Geotechnics, 2015, Oslo.
[8] ZHANG C, WHITE D, RANDOLPH M. Centrifuge modeling of the cyclic lateral response of a rigid pile in soft clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 137(7): 717-729.
[9] STEWART D, RANDOLPH M. A new site investigation tool for the centrifuge[C]//Proceedings of International Conference on Centrifuge Modelling, 1991, Boulder.
[10] HONG Y, HE B, WANG L, et al. Cyclic lateral response and failure mechanisms of semi-rigid pile in soft clay: centrifuge tests and numerical modelling[J]. Canadian Geotechnical Journal, 2017, 54(6): 806-824. doi: 10.1139/cgj-2016-0356
[11] YU J, LEUNG C F, HUANG M. Response of monopile foundations under cyclic lateral loading in normally consolidated clay[J]. International Journal of Offshore and Polar Engineering. 2018, 28(4): 411-418. doi: 10.17736/ijope.2018.jc734
[12] 俞剑, 黄茂松, 张陈蓉. 黏土中两种不同直径单桩水平循环加载模型试验与分析[J]. 岩土力学, 2016, 37(4): 973-980. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201604009.htm YU Jian, HUANG Mao-song, ZHANG Chen-rong. Model tests and analysis of single piles with two different diameters subjected to cyclic lateral loadings in clay[J]. Rock and Soil Mechanics, 2016, 37(4): 973-980. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201604009.htm
[13] USACE. Settlement Analysis Engineer Manual EM 1110-1904[S]. 1990.
[14] CRAIG W. Modeling pile installation in centrifuge experiments[C]//Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, 1985, San Francisco.
[15] ILYAS T, LEUNG C, CHOW Y, et al. Centrifuge model study of laterally loaded pile groups in clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(3): 274-283. doi: 10.1061/(ASCE)1090-0241(2004)130:3(274)
[16] FINNIE I W S. Performance of Shallow Foundations in Calcareous Soils[D]. Perth: University of Western Australia, 1993.
[17] MARTIN C, RANDOLPH M. Upper-bound analysis of lateral pile capacity in cohesive soil[J]. Géotechnique, 2006, 56(2): 141-145. doi: 10.1680/geot.2006.56.2.141
[18] EINAV I, RANDOLPH M F. Combining upper bound and strain path methods for evaluating penetration resistance[J]. International Journal for Numerical Methods in Engineering, 2005, 63(14): 1991-2016. doi: 10.1002/nme.1350
[19] ZHOU H, RANDOLPH M F. Numerical investigations into cycling of full-flow penetrometers in soft clay[J]. Géotechnique, 2009, 59(10): 801-812. doi: 10.1680/geot.7.00200
-
期刊类型引用(6)
1. 石玉琪，乐治济. 海上风电钢管复合嵌岩桩设计要素研究. 水电与新能源. 2023(01): 30-35 . 
百度学术
2. 彭文哲，赵明华，杨超炜，赵衡. 斜坡桩水平循环特性模型试验及有限杆单元解. 岩土力学. 2023(02): 381-391 . 百度学术
3. 左熹，许想，周恩全. 海上风机群桩筒基础的力学性能分析. 金陵科技学院学报. 2023(02): 40-45 . 百度学术
4. 慕东霖，田英辉，王乐，肖忠. 考虑软土软化效应时单桩基础水平循环受荷的有限元数值模拟. 岩土工程学报. 2022(04): 740-748 . 本站查看
5. 马煜祥，葛畅，贾佳，吕国儿，阮建. 桩靴式导管架基础承载特性数值模拟研究. 科技通报. 2022(08): 61-64+73 . 百度学术
6. 金丹丹，赵俣，王炳辉，李晓文. 砂土粒径变化对桩体动力响应影响的试验分析. 江苏大学学报(自然科学版). 2022(06): 704-710 . 百度学术
其他类型引用(7)
下载:
计量
- 文章访问数: 270
- HTML全文浏览量: 17
- PDF下载量: 132
- 被引次数: 13
