盾构隧道环间纵向压力时变规律研究

柳献; 杨振华; 门燕青

doi:10.11779/CJGE202101022

盾构隧道环间纵向压力时变规律研究 English Version

1.
同济大学地下建筑与工程系,上海　200092
2.
济南轨道交通集团有限公司,山东　济南　250101

基金项目:

上海市科学技术委员会科研计划项目 17DZ1203902

详细信息

作者简介:
柳献(1977— ),男,湖北武汉人,博士,教授,主要从事隧道与地下建筑结构方面的教学和科研工作。E-mail: xianliu@tongji.edu.cn

中图分类号: U45
计量
- 文章访问数: 280
- HTML全文浏览量: 29
- PDF下载量: 128
出版历程
- 收稿日期: 2020-02-18
- 网络出版日期: 2022-12-04
- 刊出日期: 2020-12-31

Temporal variation laws of longitudinal stress on cross section of shield tunnels

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
Jinan Rail Transit Group Co., Ltd., Jinan250101, China

摘要

摘要: 盾构隧道断面上受到纵向压力的大小,一方面影响环缝止水垫的防水性能；另一方面影响环缝刚度,从而影响隧道纵向不均匀沉降的发展。目前实际工程中主要依据经验估测隧道中残留的纵向力。通过求解描述隧道受力变形特征的微分方程,建立了隧道任意断面纵向力随时间的变化关系,并将理论解与现场试验实测结果进行了对比,二者具有良好的匹配性。研究结果表明,隧道纵向力在波动中下降,最终残留的纵向力大小与混凝土徐变系数和周围土体的压缩模量有关,约为掘进阶段千斤顶顶力的20.4%～44%。
- 盾构隧道 /
- 纵向力消散 /
- 拼装过程 /
- 混凝土徐变 /
- 压缩模量
Abstract: The longitudinal stress acting on the cross section of shield tunnels will affect the waterproof properties of the segments and the stiffness of the circumferential joints, which will thus affect the development trend of the longitudinal nonuniform settlements. At present, the longitudinal stress is estimated based on the experience in actual engineering. By solving the differential equation, the temporal variation laws of the longitudinal stress are proposed. The theoretical solution is also compared with meatured data from field experiments, and they matches well. The results show that the longitudinal stress decreases in fluctuations with time. The magnitude of the remaining stress is related to the creep coefficient of concrete and the compression modulus of formation. There is 20.4%~44% of the initial longitudinal stress left.
- shield tunnel /
- longitudinal stress dissipation /
- construction process /
- creep of concrete /
- compression modulus

HTML全文

0. 引言

盾构隧道施工阶段,盾构机内的千斤顶向已拼装完成的管片环施加压力,从而平衡掌子面上受到的水土压力。管片环受到的压力即使在隧道贯通后仍然不会完全消散。隧道断面上残留的纵向压力对隧道的正常使用性能有很大的影响。一方面,环缝断面上受到的纵向压力过小将导致环缝张开,进而导致环缝止水垫防水失效。另一方面,环缝断面上纵向压力减小将导致环缝的抗剪刚度和抗弯刚度大幅减小,从而使得隧道不均匀沉降加大,环缝错台,张开加剧。所以,有必要研究盾构隧道横断面上受到的纵向压力的消散规律,从而在残留的纵向力不满足使用要求时采取相应措施。

现有关于盾构隧道纵向力消散规律的理论研究较少。部分学者在隧道结构三维数值模拟中考虑了纵向力的影响^[1-3],但常认为盾构隧道纵向力在任意时刻都等于盾构机千斤顶的顶进力。这种假定夸大了横断面上的纵向力,从防水设计的角度来看会使得设计偏于不安全。Arnau等^[4]研究了隧道内纵向力随时间的变化规律。但是,其没有考虑拼装过程的影响,也没有考虑地层本身变形的影响,从而导致推导出的纵向力偏大。门燕青^[5]采用数值模拟的方法获得了纵向应力消散全过程的演变规律,主要考虑了材料应力松弛,管片间接缝的非连续性以及隧道-地层间的水平剪切效应的影响。但数值模型建模计算复杂,工程设计人员难以借此对纵向力松弛效应进行整体把握。

除理论研究外,部分学者对隧道纵向力消散规律进行了现场实测。孙肖辉等^[6]对北京槐房再生水厂污水隧道管片纵向应力进行了现场监测,其结果表明,在盾构掘进期间,管片距离盾构越远,其纵向压应力值越小；在管片拼装期间,管片距离盾构越远,其纵向压应力经历了先增大后减小的过程。廖少明等^[7]对钱江隧道纵向应力进行了长达2 a的现场监测,结果表明,纵向应力松弛将经历周期性剧烈波动、动态稳定、逐渐衰减、趋于稳定4个阶段的演变,纵向应力平均值由3 MPa逐渐松弛为1.2 MPa,在达到稳定前至少需要1 a时间。

综上所述,现有的盾构隧道纵向力消散规律理论研究假定过于理想,忽略了很多重要的影响因素。例如：没有考虑拼装过程,没有考虑地层本身的变形,没有考虑浆液硬化过程等。而现有的现场试验研究对实测纵向力分布规律的解释停留在定性的层面上,与理论缺乏联系。

本文从实际工程问题中抽象出了描述隧道纵向受力变形特征的微分方程,通过对这些微分方程进行求解,对隧道断面纵向力随时间的变化规律进行了研究。并通过敏感性分析,研究了各因素对隧道断面纵向力时变规律的影响。

1. 考虑拼装过程的盾构隧道环间纵向压力时变规律研究

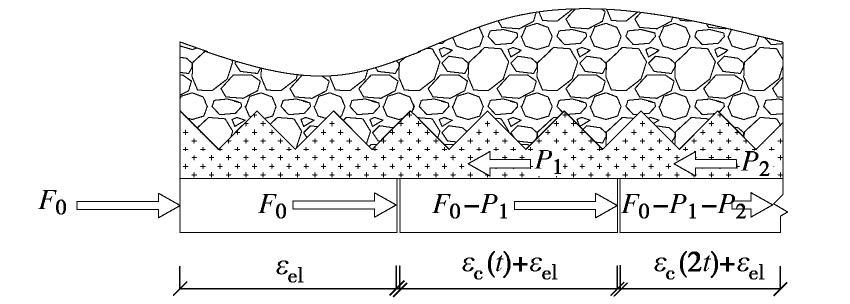
在盾构隧道施工期,盾构机掘进和管片拼装交替进行。现有研究表明^[7],掘进阶段盾构机内的千斤顶作用在管片环上的压力大于拼装阶段盾构机内的千斤顶作用在管片环上的压力。从而,掘进达到预定进尺,开始进行管片拼装的瞬时,已拼装完成的管片环会发生回弹。而隧道周围的同步注浆浆液以及浆液渗透范围内的土体将会阻止隧道回弹,同时自身在隧道回弹力的作用下伸长,如图1所示。

图 1 管片环回弹

Figure 1. Resilience of linings

下载: 全尺寸图片幻灯片

假定地层与隧道之间的相互作用力与地层和隧道之间的相对位移成正比,则地层与隧道之间的接触关系可以简化为弹簧连接。将包裹管片环的浆液、地层和管片环本身视为均质连续梁。则本问题的计算简图如图2所示。

图 2 计算简图

Figure 2. Diagram of calculation

下载: 全尺寸图片幻灯片

如图2所示,设掘进阶段盾构机千斤顶的顶进力为 $F_{0}$ ,拼装阶段盾构机的顶进力为 $F_{1}$ ,管片环刚度为E₂A₂,管片环与地层之间的连接弹簧刚度为K,管片环的位移函数为U₂(x)。值得指出的是,虽然隧道回弹不会引起地层的整体变形（由于地层和隧道体量相差悬殊）,但隧道和地层接触面附近的土层却有可能随隧道回弹发生变形,故地层刚度并非无穷大。设等效地层刚度为E₁A₁,其反映的是地层及同步注浆浆液对隧道的总约束作用。等效地层刚度一般通过三维数值模拟进行求解。首先建立隧道周边地层的三维实体模型,然后在孔洞内壁施加沿隧道轴向的均布荷载q,算得地层的最大切向位移 $Δ l$ 后,将地层对隧道约束等效为梁对隧道的约束,计算得到等效地层刚度：

$Δ l = \frac{q l^{2}}{2 E_{1} A_{1}}$ 。

(1)

最后,设地层位移函数为U₁(x)。

由于同步注浆浆液是在掘进过程中注入的,浆液和浆液渗透范围内的土体其初始应变等于掘进阶段管片环的应变,掘进阶段地层和隧道间的位移是协调的,因此,不妨设掘进阶段U₁(x)=U₂(x)=0。

首先应指出,由于掘进阶段隧道和包裹隧道的浆液、地层之间位移协调,二者之间不存在相互作用,因此,掘进阶段隧道断面纵向力就等于掘进阶段的顶进力F₀。下面求解拼装阶段隧道断面纵向力的变化规律。

以最靠近盾构机的管片环位置为原点,建立坐标系,其正方向如图2所示。由掘进阶段转换到拼装阶段的过程中,管片环位移和地层位移遵循如下平衡方程式：

$\begin{array}{l} - E_{1} A_{1} {U^{'}}_{1} (x) = \int_{0}^{x} k (U_{2} - U_{1}) d x, \\ F_{0} + E_{2} A_{2} {U^{'}}_{2}_{1} (x) = \int_{0}^{x} k (U_{2} - U_{1}) d x + F_{1} 。 \end{array}}$

(2)

此微分方程的通解为

$\begin{array}{l} U_{1} (x) = C_{1} + C_{2} x + C_{3} e^{β x} + C_{4} e^{- β x}, \\ U_{2} (x) = U_{1} (x) - \frac{E_{1} A_{1}}{K} {U^{″}}_{1} (x) 。 \end{array}}$

(3)

此微分方程遵循如下边界条件式：

$- E_{1} A_{1} {U^{'}}_{1} (0) = 0$ ,

(4)

$F_{0} + E_{2} A_{2} {U^{'}}_{2} (0) = F_{1}$ 。

(5)

方程（2）表达的位移U₁,U₂中共有4个待定参数,但实际上本文求解的环间纵向压力只与位移的导数有关,所以C₁不发挥作用,目前尚有3个待定参数。考虑到环间纵向压力不能随管片环与盾构机的距离增长而无限增大,因此,必有C₃=0。此时只余下两个参数C₂,C₄待定,将边界条件（4）和边界条件（5）代入方程（3）,即可解得拼装阶段管片环中的纵向力 $N_{2} (x)$ ：

$N_{2} (x) = \frac{E_{1} A_{1} (F_{0} - F_{1})}{E_{1} A_{1} + E_{2} A_{2}} (1 - e^{- β x}) + F_{1}$ ,

(6)

$β = \sqrt{\frac{k (E_{1} A_{1} + E_{2} A_{2})}{E_{1} A_{1} E_{2} A_{2}}}$ 。

(7)

由式（6）可知,N₂（x）是单调递增函数,当x=0时,N₂=F₁,当x=+∞时,有

$N_{2} = \frac{E_{1} A_{1} F_{0} + E_{2} A_{2} F_{1}}{E_{1} A_{1} + E_{2} A_{2}}$ 。

(8)

由此可知,拼装阶段,距离盾构机越远,管片环中的纵向力越大。正在拼装的管片环受到的纵向力最小,为拼装阶段盾构机顶进力。距离盾构机足够远（ $x = + \infty$ ）的管片环,其纵向力大小由管片环和地层的相对刚度决定,地层相对刚度越大,纵向力越大。当地层刚度远大于管片环刚度时（ $E_{1} A_{1} \to + \infty$ ）,距离盾构机足够远的管片环拼装阶段纵向力等于掘进阶段纵向力。认为某环管片拼装阶段纵向力达到拼装阶段纵向力极限值95%时,该环管片纵向力开始进入稳定状态,此时该环管片与盾构机之间的距离为

$l_{0} = - \frac{In 0.05}{β}$ 。

(9)

可以预见,与盾构机之间的距离大于l₀的管片环,拼装阶段与地层几乎达到变形协调,与地层间的相互作用力几乎为0。此过程与钢筋在混凝土中的锚固过程相似,故将l₀定义为锚固长度。

隧道贯通后,盾构机的顶进力撤除,隧道将发生回弹。这一过程类似于上文所述由掘进阶段向拼装阶段的转换过程。事实上,只要令拼装阶段盾构机千斤顶给管片的压力 $F_{1} = 0$ ,并代入式（6）中,即可求得隧道贯通后隧道内千斤顶顶力的分布N₃（x）：

$N_{3} (x) = \frac{E_{1} A_{1} F_{0}}{E_{1} A_{1} + E_{2} A_{2}} (1 - e^{- β x})$ 。

(10)

此过程中的锚固长度与掘进阶段向拼装阶段转换过程中的锚固长度完全相同。

以上描述了盾构隧道环间纵向压力的空间分布规律。事实上,假定盾构拼装速度不变,某环管片与盾构机之间的距离和该环管片拼装成环后经历的时间成正比。假定盾构每天拼装n环,则某环管片与盾构机之间的距离x和该环管片拼装成环后所经历的时间t之间有如下关系：x=nt。将此关系代入式（6）和式（10）即可得到某环管片纵向压力在隧道贯通前后的时变规律。

2. 考虑混凝土徐变效应的盾构隧道纵向力时变规律研究

混凝土在应力不变的情况下,其应变会随持荷时间的延长而增长,这种效应被称为混凝土的徐变效应。衡量混凝土徐变效应大小的物理量是混凝土的徐变系数,其定义^[8]如下

$φ (t, τ) = \frac{ε_{c} (t, τ)}{σ (τ)} E_{28}$ 。

(11)

式中, $τ$ 为混凝土的加载龄期, $ε_{c} (t, τ)$ 为t时刻的徐变应变。由式（11）可知,徐变系数是徐变应变与28 d龄期混凝土加载瞬时产生的弹性应变的比值。

管片混凝土徐变会显著影响隧道内纵向力的分布。具体而言,随着管片环受压时间的增长,管片徐变应变增长,周围地层将会约束管片,防止其应变增长,从而地层和已经凝固的浆液会对管片产生作用力,这种作用力方向与隧道断面上的纵向压力相反,从而导致隧道断面上纵向力的减小,隧道断面纵向力的减小又将导致隧道弹性应变减小,从而造成隧道内纵向力新一轮的重分布。总而言之,由管片环混凝土徐变导致的纵向力重分布是一个不断迭代,逐步稳定的过程,如图3所示。

图 3 徐变引起的应力重分布效应

Figure 3. Redistribution of stress caused by creep of linings

下载: 全尺寸图片幻灯片

混凝土徐变对隧道纵向力分布的影响存在一个复杂的调整过程,但是其最终结果与应力重分布的过程无关。可以预见,锚固长度外的管片环,其变形与地层几乎完全协调。由此可知,在这部分管片环中,徐变应变等于弹性应变的减小量,管片的总应变不随时间变化而变化：

$\begin{array}{l} ε_{c} (t) = ε_{c} (t_{0}), \\ ε_{c} (t) = [\frac{σ_{c} (t_{0})}{E_{c}} + \frac{Δ σ_{c} (t, t_{0})}{E_{c}}] [1 + φ (t, t_{0})] 。 \end{array}}$

(12)

式中, $ε_{c} (t_{0})$ 为管片开始受压时的弹性应变, $ε_{c} (t)$ 为t时刻管片的总应变, $σ_{c} (t_{0})$ 为管片开始受压时的应力, $Δ σ_{c} (t, t_{0})$ 为t时刻管片中应力相比于t₀时刻管片中应力的减小量。求解式（12）可以得到t时刻压应力 $σ_{c} (t)$ 与t₀时刻管片中压应力 $σ_{c} (t_{0})$ 的关系：

$σ_{c} (t) = σ_{c} (t_{0}) [1 - \frac{φ (t, t_{0})}{1 + φ (t, t_{0})}]$ 。

(13)

所以,在考虑徐变效应的情形下,管片环拼装阶段纵向力 $N_{2} (t)$ 的时变规律为

$\begin{array}{l} N_{2} (t) = [\frac{E_{1} A_{1} (F_{0} - F_{1})}{E_{1} A_{1} + E_{2} A_{2}} (1 - e^{- β n t}) + F_{1}] \cdot ψ, \\ ψ = 1 - \frac{φ (t, t_{0})}{1 + φ (t, t_{0})} 。 \end{array}}$

(14)

式中,n表示盾构拼装速度（环/d）。

掘进阶段管片环纵向力 $N_{1} (t)$ 的时变规律：

$N_{1} (t) = F_{0} \cdot [1 - \frac{φ (t, t_{0})}{1 + φ (t, t_{0})}]$ 。

(15)

隧道贯通后,徐变引起隧道纵向力衰减的规律与施工阶段完全相同,所以,隧道贯通后纵向力的时变规律为

$\begin{array}{l} N_{3} (x, t) = \frac{E_{1} A_{1} F_{0}}{E_{1} A_{1} + E_{2} A_{2}} (1 - e^{- β x_{0}}) \cdot ψ, \\ ψ = 1 - \frac{φ (t, t_{0})}{1 + φ (t, t_{0})} 。 \end{array}}$

(16)

式中,x₀为计算点到隧道洞口的距离。

由于地层体量远大于隧道,地层刚度E₁A₁常为隧道刚度E₂A₂的十倍以上,其对残留纵向力大小的影响较小。由式（15）可知,在距离洞口足够远的位置,隧道贯通后其断面上残留的纵向力几乎完全由徐变系数决定。由《公路钢筋混凝土及预应力混凝土桥涵设计规范：JTG D62—2004》^[9]中规定可知,在持荷时间无限长时,徐变系数的取值范围为1.28～3.9,代入式（15）,算得隧道中最终残留的纵向力约占掘进阶段千斤顶总推力的20.4%～44%。

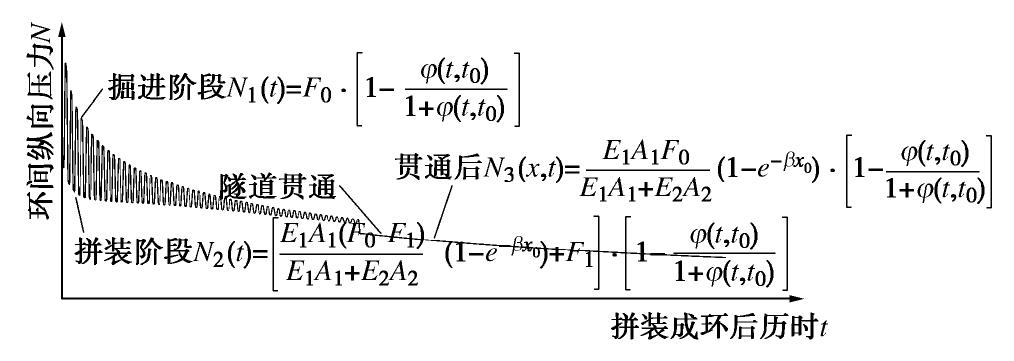
综上所述盾构隧道环间纵向压力的时变规律受到隧道回弹和混凝土徐变效应的双重影响。某环管片所受到的纵向压力和该环管片拼装成环后历时的关系如图4所示。

图 4 环间纵向压力时变曲线

Figure 4. Changing curve of longitudinal force

下载: 全尺寸图片幻灯片

由图4可知,某环管片拼装成环后,其所受到的环间纵向压力在波动中下降。波动量逐渐减小,环间纵向压力的下降速率也逐渐减小,直至达到稳定。

3. 理论模型的试验验证

3.1 试验概况

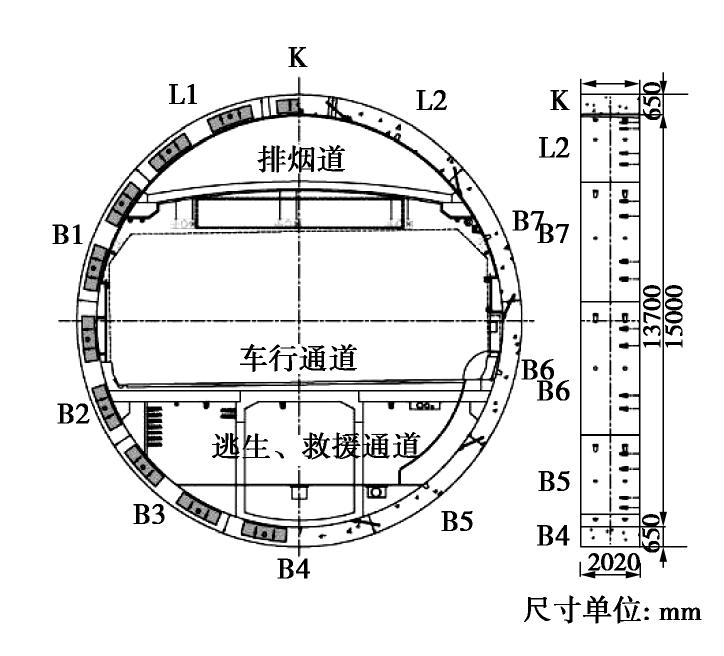
钱江隧道是当前世界上已建成通车的最大直径的软土盾构法隧道工程之一^[10]。盾构段隧道采用圆形断面,单层衬砌的结构形式,衬砌环外径15.00 m,内径13.70 m,管片厚度0.65 m,环宽度2.0 m,采用“9+1”（B1～B7、L1、L2、K）通用楔形环分块方式,环间错缝拼装,环、块间采用斜螺栓连接。管片混凝土强度等级C60。隧道结构及内部布置如图5所示。

图 5 钱江隧道结构及内部布置图

Figure 5. Structure of Qianjiang tunnel

下载: 全尺寸图片幻灯片

盾构段隧道穿越土层主要为透水性强的粉砂层和强度低,含水率高,灵敏度高的淤泥质黏土层。隧址位于钱塘江赶潮河段,以非正规浅海半日潮为主的潮汐现象明显、潮差较大。廖少明等^[7]在隧道第618环内部,隧道第618环和第619环环间接触面上布置了钢筋计,应变计,和纵向测力螺栓等元件,对隧道纵向力变化进行了长达2 a的测量。

3.2 理论模型参数

本文中徐变系数的取值采用《公路钢筋混凝土及预应力混凝土桥涵设计规范：JTG D62—2004》^[9]中规定。适用于本工程的混凝土徐变本构关系为

$ϕ (t, t_{0}) = 1.99 \times {[\frac{(t - t_{0}) / t_{1}}{1225 + (t - t_{0}) / t_{1}}]}^{0.3}$ 。

(17)

其中 $ϕ (t, t_{0})$ 为t时刻混凝土的徐变系数, $t_{0}$ 为混凝土管片的加载龄期, $t_{1} = 1 d$ 。

由文献[7]可知,掘进阶段盾构机千斤顶顶进力基本在80～100 MN附近波动,所以,将隧道掘进阶段的纵向力F₀近似取为90 MN。拼装阶段盾构机千斤顶顶力基本为50～80 MN,故令F₁=65 MN。依据盾构机的掘进记录,2012-06-03日—2013-01-18日共计225 d的时间内,隧道从第601环拼装至第1320环,共计拼装720环,平均每天拼装3.2环。

依据文献[10],算得连接刚度K为

$K = \frac{E_{S} P_{e}}{3 R (1 + ν)} = 7.4 (MPa)$ 。

(18)

式中, $E_{S}$ 为周围地层和硬化同步注浆浆液组成的混合物的弹性模量,R为隧道的半径, $ν$ 为周围地层和硬化同步注浆浆液组成的混合物的泊松比,P_e为隧道周长。

地层刚度E₁A₁采用数值模型进行计算。沿隧道横向水平方向和竖直方向的计算域取为隧道长度的10倍,沿隧道纵向的计算域取为隧道长度3245 m,算得地层刚度为 $E_{1} A_{1} = 3.04 \times 10^{10} kN$ 。

本工程隧道断面外径15 m,内径13.7 m,所以,管片环刚度为 $E_{2} A_{2} = 1.054 \times 10^{6} MN$ 。

3.3 理论纵向力时变曲线与实测值对比

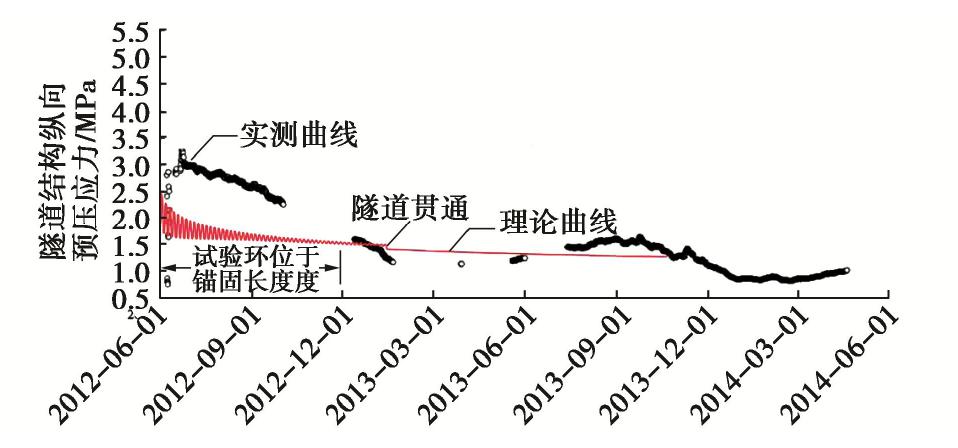
由文献[5]可知,实测纵向应力时变曲线如图6所示,在同一坐标系中做出理论纵向应力时变曲线。

图 6 理论纵向力时变曲线

Figure 6. Theoretical curve of temporal variation of longitudinal stress

下载: 全尺寸图片幻灯片

由图6可知,实测隧道断面纵向应力与理论隧道断面纵向应力变化趋势一致,均在波动中下降。不论是实测断面纵向应力还是理论断面纵向应力,在管片拼装成环后短时间内,其波动量均很大,随后其波动量逐渐减小,直至稳定。稳定阶段实测纵向应力和理论纵向应力大小均为1 MPa左右,二者具有良好的匹配性。

由图6可知,理论曲线和试验曲线在后期（180 d以后）符合较好,而在前期与试验曲线差距较大,具体表现为180 d前,实测纵向力大于理论推导得出的纵向力。其原因是考虑徐变作用时纵向力的衰减因子为

$1 - \frac{φ}{1 + φ}$ 。

(19)

是针对锚固长度外的管片提出的。对于锚固长度以内的管片,由于其与地层之间尚未达到变形协调,所以徐变应变的增长量不等于弹性应变的减小量,采用锚固长度以外管片的徐变折减系数实际上高估了徐变造成的纵向力衰减。

针对于本次现场试验,锚固长度 $l_{0}$ 为

$l_{0} = - \frac{I n 0.05}{β} = 1105 (m)$ 。

(20)

按照每天掘进3.2环的速度,试验环推出锚固长度需要172.6 d,从而在172.6 d以内,理论推导出的试验环纵向力将小于实测试验环纵向力,在172.6 d之后理论推导出的纵向力将于实测纵向力基本相同。这一结论与事实相符,从而说明了上述误差分析过程的合理性。

4. 盾构隧道纵向力时变规律影响因素敏感性分析

纵向力时变规律影响因素众多,有必要分析各因素对纵向压力影响的大小,以便于在工程中进行重点控制。

贯通后断面残留纵向力是影响隧道纵向受力性能的主要因素。将其取为系统的输出变量。影响贯通后隧道断面残留纵向力的主要因素有掘进阶段的顶进力,地层压缩模量,以及管片的加载龄期。将隧道掘进阶段顶进力,地层压缩模量,掘进速度,管片加载龄期4个物理量作为系统的输入变量。不妨将敏感性系数取为系统输出变量对系统输入变量的一阶偏导数^[11-12]。

由于各输入变量单位和取值范围均有不同,故首先对其进行归一化处理。假定某一因素的变化范围为 $(X_{\min}, X_{\max})$ ,则该因素的某一取值x进行归一化为

$\hat{X} = \frac{X - X_{\min}}{X_{\max} - X_{\min}}$ 。

(21)

不难看出,经过归一化后,输入变量的取值范围将统一变为（0,1）。

以下分析中所采用的参数与第4节现场试验中参数相同。

由式（6）,（7）可知,地层压缩模量一方面影响公式中的等效地层刚度E₂A₂,另一方面影响系数β。等效地层刚度E₂A₂一般情况下其远大于隧道本身的刚度,从而其对贯通后隧道断面残余纵向力的影响有限,出于简化计算的考虑,不计等效地层刚度的影响,从而,贯通后隧道断面纵向力与地层压缩模量的关系为

$\begin{array}{l} N_{3} (x) = F_{0} (1 - e^{- \sqrt{\frac{P_{e} E_{s}}{3 R (1 + ν) E_{1} A_{1}}} x}) \cdot ψ, \\ ψ = 1 - \frac{φ (t, t_{0})}{1 + φ (t, t_{0})} 。 \end{array}}$

(22)

断面残余纵向力N₃对地层压缩模量 $E_{s}$ 求偏导数,并考虑地层压缩模量在实际地层压缩模量±10%的范围内变化（3.96～4.84 MPa）,进行归一化处理,可得敏感性系数为

$\frac{\partial N_{3}}{\partial {\hat{E}}_{s}} = 0.88 \frac{\partial N_{3}}{\partial E_{s}} = 0 .257$ 。

(23)

下面分析隧道掘进阶段顶进力对贯通后隧道断面残留纵向力的影响。断面残余纵向力 $N_{3}$ 对掘进阶段顶进力 $F_{0}$ 求偏导数,并考虑掘进阶段顶进力在实际掘进阶段顶进力±10%的范围内变化（81～99 MN）,进行归一化处理,可得敏感性系数为

$\frac{\partial N_{3}}{\partial {\hat{F}}_{0}} = \frac{\partial N_{3}}{\partial F_{0}} \frac{\partial F_{0}}{\partial {\hat{F}}_{0}} = 5.88$ 。

(24)

下面考虑管片加载龄期对贯通后隧道断面残留纵向力的影响。断面残余纵向力N₃对管片加载龄期t₀求偏导数,并考虑管片加载龄期在实际管片加载龄期±10%的范围内变化（25.2～30.8 d）,进行归一化处理,可得敏感性系数为

$\frac{\partial N_{3}}{\partial {\hat{t}}_{0}} = \frac{\partial N_{3}}{\partial t_{0}} \frac{\partial t_{0}}{\partial {\hat{t}}_{0}} = 0.6$ 。

(25)

综上所述,掘进阶段顶进力的敏感性系数最大,管片加载龄期的敏感性系数次之,地层压缩模量的敏感性系数最小。从而,对隧道贯通后断面残留纵向力影响最大的因素是掘进阶段的顶进力,其次是管片的加载龄期,对隧道贯通后断面残留纵向力影响最小的因素是地层压缩模量。

5. 结论与建议

本文通过理论推导,建立了盾构隧道任意断面纵向力随推出盾尾时间的变化规律,并将其与钱江隧道实测纵向力变化规律进行了对比,得到以下两点结论。

（1）施工期拼装阶段隧道断面纵向压力时变规律如式（14）所示,施工期掘进阶段隧道断面纵向压力时变规律如式（15）所示,贯通后隧道断面纵向压力时变规律如式（16）所示。

（2）纵向压力隧道断面上最终残留的纵向力约占掘进阶段顶进力的20.4%～44%。

在实际工程中,建议对管片进行足时的养护以增大隧道中残留的纵向力,改善隧道的使用性能。建议采用掘进拼装同步的施工方法（从根本上消除波动原因）和采用强度更高的同步注浆浆液,以减小隧道中纵向力的波动时间。

图 1 管片环回弹

Figure 1. Resilience of linings

下载: 全尺寸图片幻灯片

图 2 计算简图

Figure 2. Diagram of calculation

下载: 全尺寸图片幻灯片

图 3 徐变引起的应力重分布效应

Figure 3. Redistribution of stress caused by creep of linings

下载: 全尺寸图片幻灯片

图 4 环间纵向压力时变曲线

Figure 4. Changing curve of longitudinal force

下载: 全尺寸图片幻灯片

图 5 钱江隧道结构及内部布置图

Figure 5. Structure of Qianjiang tunnel

下载: 全尺寸图片幻灯片

图 6 理论纵向力时变曲线

Figure 6. Theoretical curve of temporal variation of longitudinal stress

下载: 全尺寸图片幻灯片

参考文献(12)

[1]	BLOM C B M, HORST E J V D, JOVANOVIC P S. Three-dimensional structural analyses of the shield-driven “Green Heart” tunnel of the high-speed line south[J]. Tunnelling & Underground Space Technology, 1999, 14(2): 217-224.
[2]	KLAPPERS C, GRÜBL F, OSTERMEIER B. Structural analyses of segmental lining - coupled beam and spring analyses versus 3D-FEM calculations with shell elements[J]. Tunnelling and Underground Space Technology, 2006, 21(3).
[3]	MO H H, CHEN J S. Study on inner force and dislocation of segments caused by shield machine attitude[J]. Tunnelling and Underground Space Technology, 2008, 23(3): 281-291. doi: 10.1016/j.tust.2007.06.007
[4]	ARNAU O, MOLINS C, BLOM C B M, et al. Longitudinal time-dependent response of segmental tunnel linings[J]. Tunnelling and Underground Space Technology, 2011, 28(1): 98.
[5]	门燕青. 盾构法隧道纵向应力松弛的发生机理及其效应[D]. 上海: 同济大学, 2017. MEN Yan-qing. The Origination and Effect of Longitudinal Stress Relaxation Along the Shield Tunnel[D]. Shanghai: Tongji University, 2017. (in Chinese)
[6]	孙肖辉, 马孝春, 黄峰, 等. 小直径盾构施工中管片纵向应力监测研究[J]. 隧道建设(中英文), 2017, 37(11): 1436-1441. doi: 10.3973/j.issn.2096-4498.2017.11.012 SUN Xiao-hui, MA Xiao-chun, HUANG Feng, et al. Study of monitoring of longitudinal stress of small-diameter shield tunnel segment during construction[J]. Tunnel Construction, 2017, 37(11): 1436-1441. (in Chinese) doi: 10.3973/j.issn.2096-4498.2017.11.012
[7]	廖少明, 门燕青, 肖明清, 等. 软土盾构法隧道纵向应力松弛规律的实测分析[J]. 岩土工程学报, 2016, 39(5): 795-803. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705005.htm LIAO Shao-ming, MEN Yan-qing, XIAO Ming-qing, et al. Field tests on longitudinal stress relaxation along shield tunnel in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 795-803. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705005.htm
[8]	CEB-FIP. CEB-FIP Model Code 1990[S]. London: Thomas Telford, 1993.
[9]	公路钢筋混凝土及预应力混凝土桥涵设计规范：JTG D62—2004[S]. 北京: 人民交通出版社, 2004. Code for Design of High Way Reinforced Concrete and Prestressed Concrete Bridge and Culverts: JTG D62—2004[S]. Beijing: Chinese Communications Publishing, 2004. (in Chinese)
[10]	KOEK A J. Axiale voorspanning in de lining van een geboorde tunnel[D]. Delft: Delft University of Technology, 2004. (in Dutch)
[11]	SALTELLI A. Sensitivity Analysis[M]. Chichester: Wiley, 2000.
[12]	蔡毅, 邢岩, 胡丹. 敏感性分析综述[J]. 北京师范大学学报(自然科学版), 2008, 44(1): 9-16. https://www.cnki.com.cn/Article/CJFDTOTAL-BSDZ200801004.htm CAI Yi, XING Yan, HU Dan. On sensitivity analysis[J]. Journal of Beijing Normal University (Natural Science), 2008, 44(1): 9-16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BSDZ200801004.htm

施引文献(18)

期刊类型引用(12)

1.	江学辉，颜建伟，罗文俊，李佳宝，徐长节. 纵向压力和加固钢板对隧道力学性能影响的解析解. 岩土力学. 2024(06): 1623-1632 . 百度学术
2.	张中安，潘野，郭振坤，张姣龙，高一民，柳献. 基于既有盾构隧道区间暗挖施工的城市轨道交通车站结构力学行为研究. 城市轨道交通研究. 2024(08): 129-136+142 . 百度学术
3.	任璐瑶，吴镇杰，黄啟超，关振长. 考虑轴力影响的盾构隧道纵向地震响应解析. 岩土力学. 2024(10): 2971-2980 . 百度学术
4.	周龙，朱合华，沈奕，闫治国，官林星. 内水压盾构隧道管片衬砌受力与变形特性分析. 岩土工程学报. 2023(09): 1763-1772 . 本站查看
5.	郦亮，谢长岭，冯立力，贾立翔，张文轩. 一种新型光纤光栅应变计的温度补偿方法研究. 城市轨道交通研究. 2023(12): 179-183 . 百度学术
6.	罗旭，秦楠，叶宇航，高学奎，徐文田，柳献. 纵向力对快速连接件管片环缝剪切性能影响研究. 隧道建设(中英文). 2023(S2): 246-251 . 百度学术
7.	周龙，朱合华，闫治国，沈奕，孙巍，李耀良. 深埋高内水压盾构隧道管片衬砌力学特性足尺试验研究. 土木工程学报. 2022(09): 94-105+117 . 百度学术
8.	柳献，焦伯昌，潘伟强，黄爱军. 大断面钢结构顶管纵向力时变规律研究. 岩土工程学报. 2022(10): 1810-1816 . 本站查看
9.	林菲菲. 基于LSTM网络的地铁隧道运营期间沉降预测研究. 广东土木与建筑. 2022(10): 45-48 . 百度学术
10.	杨振华. 浅覆土接收盾构隧道环间压力分布规律研究. 现代隧道技术. 2022(05): 18-26 . 百度学术
11.	张旦旦. 盾构隧道混凝土管片预制工艺及质量控制措施. 建材发展导向. 2022(24): 184-186 . 百度学术
12.	毛赵武. 盾构通过矿山法施工隧道段关键技术研究. 智能城市. 2021(06): 154-155 . 百度学术