基于微结构张量的岩石各向异性弹塑性本构及其应用

殷达; 孟庆祥; 徐建荣; 石安池; 吴关叶; 徐卫亚

doi:10.11779/CJGE202009020

基于微结构张量的岩石各向异性弹塑性本构及其应用 English Version

殷达^{1, 2, 3,},
孟庆祥^{1, 2},
徐建荣⁴,
石安池⁴,
吴关叶⁴,
徐卫亚^{1, 2, ,}

1.
河海大学岩土力学与堤坝工程教育部重点实验实,江苏　南京　210024
2.
河海大学岩土工程科学研究所,江苏　南京　210024
3.
中交广州航道局有限公司,广东　广州　510290
4.
中国电建集团华东勘测设计研究院有限公司,浙江　杭州　310014

基金项目:

国家重点研发计划项目 2018YFC0407004

国家自然科学基金项目 51939004

国家自然科学基金项目 51709089

国家自然科学基金项目 51609070

中央高校基本科研业务费专项资金项目 B200202083

详细信息

作者简介:
殷达(1994—),男,硕士,主要从事岩石力学与工程等方面的研究工作。E-mail：yinda94@hhu.edu.cn

通讯作者:
徐卫亚, E-mail：wyxuhhu@163.com

中图分类号: TU432
计量
- 文章访问数: 229
- HTML全文浏览量: 23
- PDF下载量: 146
出版历程
- 收稿日期: 2019-05-04
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-08-31

Anisotropic elastoplastic constitutive model based on microstructure tensor and its engineering application

YIN Da^{1, 2, 3,},
MENG Qing-xiang^{1, 2},
XU Jian-rong⁴,
SHI An-chi⁴,
WU Guan-ye⁴,
XU Wei-ya^{1, 2, ,}

1.
Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210024, China
2.
Jiangsu Research Center for Geotechnical Engineering Technology, Hohai University, Nanjing 210024, China
3.
CCCC Guangzhou Dredging Co., Ltd., Guangzhou 510290, China
4.
PowerChina, Huadong Engineering Corporation, Hangzhou 310014, China

摘要

摘要: 提出了一种基于微结构张量理论的各向异性弹塑性本构关系,引入了微结构张量表征横观各向同性材料强度参数的空间分布函数,将莫尔–库仑准则拓展到各向异性。基于FLAC^3D实现了自定义本构模型的二次开发,对柱体倾角为75°的柱状节理试样进行了三轴数值试验模拟,模拟结果与实验成果基本吻合验证了模型的合理性。将所开发本构模型应用于白鹤滩高坝坝基开挖工程的数值仿真计算,结果表明：坝基岩体开挖工况下各向异性模型较各向同性模型的变形特征更接近于现场监测。研究成果可为白鹤滩水电工程建设提供理论参考。
- 微结构张量 /
- 各向异性 /
- 弹塑性本构 /
- 柱状节理 /
- 白鹤滩水电站
Abstract: An anisotropic elastoplastic constitutive relation based on the microstructure tensor theory is proposed. The microstructure tensor is introduced to describe the spatial distribution function of the strength parameters of transversely isotropic materials. The user defined model is developed in FLAC^3D, and the triaxial numerical simulation tests on columnar jointed specimen with a joint angle of 75° are carried out. The simulated results are in good agreement with the experimental ones, indicating the feasibility of the model. The developed constitutive model is also applied to the numerical simulation calculation of the excavation of the foundation of Baihetan high dam. The results show that the deformation characteristics of the anisotropic model are closer to the actual monitoring results than thoes of the isotropic model. The results can provide theoretical support for the construction of Baihetan Hydropower Station.
- microstructure tensor /
- anisotropy /
- elastoplastic constitutive /
- columnar joint /
- Baihetan Hydropower Station

HTML全文

0. 引言

柱状节理常见于玄武岩岩体,节理面独特的空间结构分布使得岩体强度表现出强各向异性。已有学者针对柱状节理岩体开展了现场原位试验和大量的相似材料室内试验^[1-5],验证了柱状节理岩体的强度各向异性并总结了材料强度参数的各向异性分布规律。但目前对于柱状节理岩体各向异性本构研究的报道还不多,而已有的一些各向同性模型则不能很好的描述柱状节理岩体的强度各向异性特性。

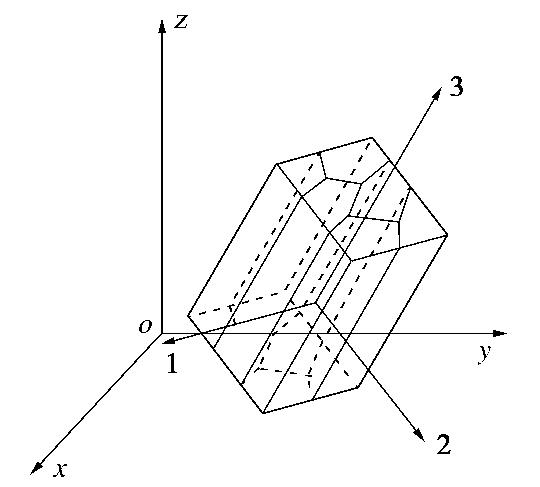
柱状节理岩体为岩块和结构面的综合体,其表征单元体较室内试验可研究的尺度要大许多,很难通过室内试验来研究柱状节理岩体的变形和强度特征。而原位试验虽然可以在一定程度上反映节理岩体的工程力学特性,但受限于场地、设备、成本等因素,一些物理力学参数难以获取。由于柱状节理岩体具有结构周期性,可以应用数值均匀化方法开展多尺度分析计算,如多重有限元（FE²）或跨尺度有限元离散元耦合（FEM/DEM）。该类方法避免了复杂本构方程的建立,适用于满足均匀化条件的复杂细观结构材料。但多尺度方法计算量巨大,难以直接应用于大型水电工程的计算。因此建立可以准确描述柱状节理岩体力学特性的本构模型具有重要意义。柱状节理岩体显著的各向异性是本构的建模的难点。微结构张量作为材料微观结构的一种度量,可用来描述岩体介质中孔隙或裂纹的空间分布。本文在传统力学模型的基础上引入微结构张量,建立柱状节理岩体各向异性本构模型。

Kanatani^[6-7]最早系统研究了材料空间分布与微结构张量的关系,初步建立了空间分布函数的表达式。Pietruszczak等^[8]通过组合强度参数的空间分布,把经典各向同性准则拓展为各向异性,建立了基于微结构张量的各向异性屈服准则。Gao等^[9]将微结构张量参数引入屈服函数,提出了一种具有交叉各向异性的岩土材料的广义破坏准则,该准则在描述大范围材料的强度随加载方向的变化时具有通用性和鲁棒性。钟世英等^[10]采用多组节理面局部坐标系与整体坐标系的投影关系定义了材料空间的微结构张量表达,将其引入莫尔库仑强度准则,得到了多组节理岩体的各向异性强度准则。

然而现阶段基于微结构张量的各向异性本构模型尚存在不足,或以页岩等层状岩石为研究对象^[8-9],模型不能较好反映柱状节理岩体物理力学试验特性,或模型较为复杂,参数不易确定^[10],实际应用较为困难。

为此,本文提出了一种既保留了数学的严谨性又具有一定实用性的方法。首先,结合微结构张量理论推导了柱状节理岩体各向异性弹塑性本构积分公式,然后基于FLAC^3D对自定义本构进行了二次开发,并结合柱状节理相似结构材料三轴岩石力学试验对本文提出的自定义本构模型进行了验证。应用所开发各向异性弹塑性本构模型对白鹤滩水电站坝基开挖工程进行了数值模拟分析,数值模拟结果与坝基岩体开挖工程监测结果基本相符。研究结果对白鹤滩水电工程建设具有一定应用价值。

1. 各向异性弹塑性本构

1.1 弹性刚度矩阵及空间旋转变换

理想弹性体的本构关系可表示为

$ε = C σ$ 。

(1)

柱状节理岩体（如图1）可简化为横观各向同性材料,由广义胡克定律,在材料空间的局部坐标系下其柔度矩阵可表示为

图 1 全局坐标系中的柱状节理材料

Figure 1. Cylindrical joint materials in global coordinate system

下载: 全尺寸图片幻灯片

$\begin{matrix} C = [\begin{matrix} \frac{1}{E_{1}} & - \frac{ν_{12}}{E_{1}} & - \frac{ν_{13}}{E_{3}} & 0 & 0 & 0 \\ - \frac{ν_{12}}{E_{1}} & \frac{1}{E_{1}} & - \frac{ν_{13}}{E_{3}} & 0 & 0 & 0 \\ - \frac{ν_{13}}{E_{3}} & - \frac{ν_{13}}{E_{3}} & \frac{1}{E_{3}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{G_{13}} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{G_{13}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{2 (1 + ν_{12})}{E_{1}} \end{matrix}] \\ = {[D^{e}]}^{- 1} \end{matrix}$ ,

(2)

式中, $E_{1}$ 为平行于各向同性面的弹性模量, $E_{3}$ 为垂直于各向同性面的弹性模量, $G_{13}$ 为垂直平面的剪切模量, $ν_{12}$ 为平行面内的泊松比, $ν_{13}$ 为垂直方向的泊松比, $D^{e}$ 为弹性刚度矩阵。

全局坐标系下的柔度矩阵 $C^{'}$ 可由局部坐标系下的柔度矩阵 $C$ 旋转得到

$C^{'} = Q^{T} C Q$ ,

(3)

式中, $Q$ 为一个包含局部坐标轴与全局坐标轴夹角 $α$ 的二阶张量,可表示为

$Q = [\begin{matrix} \cos^{2} α & \sin^{2} α & 0 & \frac{\sin 2 α}{- 2} & 0 & 0 \\ \sin^{2} α & \cos^{2} α & 0 & \frac{\sin 2 α}{2} & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \sin 2 α & - \sin 2 α & 0 & \cos 2 α & 0 & 0 \\ 0 & 0 & 0 & 0 & \cos α & - \sin α \\ 0 & 0 & 0 & 0 & \sin α & \cos α \end{matrix}]$ 。

(4)

对于横观各向同性材料,需要给出两个夹角,分别为材料的倾向 $α$ 和倾角 $β$ 。后续推导若不加说明,默认在材料空间中的局部坐标系展开。

1.2 各向异性屈服函数及塑性势函数

定义微结构张量 $a_{i j}$ 主轴与材料空间的局部坐标系同轴,三维空间中微结构张量 $a_{i j}$ 可由单位向量 $e_{i}$ 表示为

$\begin{matrix} a_{i j} = a_{1} e_{i}^{(1)} e_{j}^{(1)} + a_{2} e_{i}^{(2)} e_{j}^{(2)} + e_{i}^{(3)} e_{j}^{(3)} \\ = a_{1} m_{i j}^{(1)} + a_{2} m_{i j}^{(2)} + a_{3} m_{i j}^{(3)} \end{matrix}$ ,.

(5)

式中, $a_{i}$ 为微结构张量的主值, $m_{i j}$ 为结构取向张量。

定义广义加载单位向量 $l_{i}$ 为

$l_{i} = \frac{L_{i}}{\sqrt{L_{k} L_{k}}} = \frac{L_{i}}{\sqrt{σ_{i j} σ_{i j}}} = \frac{L_{i}}{\sqrt{tr σ^{2}}}$ ,

(6)

$L_{i} = \sum_{x = 1}^{3} L_{x} e_{i}^{(x)}$ ,

(7)

$L_{x} = \sqrt{σ_{1 x}^{2} + σ_{2 x}^{2} + σ_{3 x}^{2}}$ 。

(8)

考虑微结构张量 $a_{i j}$ 在 $l_{i}$ 方向上的投影,即

$\begin{matrix} η = a_{i j} l_{i} l_{j} = a_{1} \frac{tr(m^{(1)} σ^{2})}{tr σ^{2}} + a_{2} \frac{tr(m^{(2)} σ^{2})}{tr σ^{2}} + \\ a_{3} \frac{tr(m^{(3)} σ^{2})}{tr σ^{2}} \end{matrix}$ 。

(9)

式（9）所定义参数 $η$ 是一个无量纲的标量,综合考虑了材料结构面取向对加载空间的影响,反映了材料强度的方向依赖性,因此可用来描述材料强度的各向异性空间分布。式（9）也可表示为偏量的形式：

$η = \hat{η} (1 + A_{i j} l_{i} l_{j})$ ,

(10)

$\hat{η} = a_{k k} / 3, A_{i j} = (a_{i j} - \hat{η} δ_{i j}) / \hat{η}$ 。

(11)

式（10）最早由Kanatani^[6-7]提出。更一般的,该式可表示为

$\begin{matrix} η = \hat{η} (1 + A_{i j} l_{i} l_{j} + A_{i j k l} l_{i} l_{j} l_{k} l_{l} + \dots) \\ = \hat{η} (1 + A_{i j} l_{i} l_{j} + b_{1} {(A_{i j} l_{i} l_{j})}^{2} + \dots) \end{matrix}$ 。

(12)

本文采用一种修正的莫尔库仑准则^[11]来描述岩石柱体的塑性行为,并考虑各向异性和塑性硬化：

$\begin{matrix} f = \sqrt{{(q K (θ))}^{2} + {(e_{f} c \cos ϕ)}^{2}} + \\ η_{f} h (ξ) (p \sin ϕ - c \cos ϕ) \end{matrix}$ ,

(13)

$\begin{matrix} p = \frac{σ_{k k}}{3},_{}^{} {_{}^{}}_{}^{}_{}^{} q = \sqrt{\frac{3}{2} J_{2}}, \\ J_{2} = s_{i j} s_{i j},_{}^{} {_{}^{}}_{}^{}_{}^{} s_{i j} = σ_{i j} - \frac{σ_{k k}}{3} δ_{i j} \end{matrix}$ 。

(14)

式中 $c$ 为材料黏聚力, $ϕ$ 为材料内摩擦角,可通过试验确定； $e_{f}$ 为子午面上拟合屈服线的双曲偏心率,可通过调整 $e_{f}$ 来调整抗拉强度大小； $η_{f}$ 为微结构张量参数, $h (ξ)$ 为塑性硬化函数, $ξ$ 为塑性内变量； $p$ 为平均应力, $q$ 为偏应力, $J_{2}$ 为应力偏量第二不变量, $θ$ 为Lode角, $K (θ)$ 为关于Lode角的函数。

Lode角函数采用分段形式对屈服面角点进行平滑修正：

$K (θ) = {\begin{matrix} \cos θ - \frac{\sin θ \cos ϕ}{\sqrt{3}} & | θ | \leq θ_{t} \\ K_{1} - K_{2} \sin 3 θ & | θ | > θ_{t} \end{matrix}$ ,

(15)

$\begin{matrix} K_{1} = \frac{1}{3} \cos θ_{t} (3 + \tan θ_{t} \tan 3 θ_{t} + \\ \frac{1}{\sqrt{3}} (\tan 3 θ_{t} - 3 \tan θ_{t}) sign(θ) \sin ϕ) \end{matrix}$ ,

(16)

$K_{2} = \frac{1}{3 \cos 3 θ_{t}} (sign(θ) \sin θ_{t} + \frac{1}{\sqrt{3}} \sin θ_{t} \sin ϕ)$ ,

(17)

式中, $θ_{t}$ 为容许Lode角,当 $| θ | \leq θ_{t}$ 时,与经典Mohr–Coulomb准则一致,当 $| θ | > θ_{t}$ 时,对屈服函数迹线进行平滑处理。

取等效塑性剪应变 ${\bar{γ}}^{p}$ 作为塑性内变量,定义塑性硬化函数为^[12]

$h (ξ) = h_{0} - (h_{1} - h_{0}) \frac{ξ}{B + ξ}$ ,

(18)

$ξ = {\bar{γ}}^{p} = \int d {\bar{γ}}^{p},_{}^{} {_{}^{}}_{}^{} d {\bar{γ}}^{p} = \sqrt{\frac{2}{3} d e_{i j}^{p} d e_{i j}^{p}}$ ,

(19)

式中, $h_{0}$ 为初始屈服阈值, $h_{1}$ 为峰值屈服阈值, $B$ 为描述塑性硬化率大小的参数。

塑性势函数与屈服函数形式一致,即

$g = \sqrt{q^{2} K^{2} (θ) + {(e_{f} c \cos ψ)}^{2}} + η_{f} p \sin ψ$ ,

(20)

式中, $ψ$ 为膨胀角,当 $ψ \neq ϕ$ 时即为非关联流动。

1.3 屈服函数及塑性势函数求导

由于本构数值积分中将涉及到屈服函数及塑性势函数的偏导数,故先行给出偏导数的求解。首先计算屈服函数对应力张量的偏导数,根据式（13）有

$\frac{\partial f}{\partial σ_{i j}} = (\frac{\partial f}{\partial I_{1}} \frac{\partial I_{1}}{\partial σ_{i j}} + \frac{\partial f}{\partial J_{2}} \frac{\partial J_{2}}{\partial σ_{i j}} + \frac{\partial f}{\partial θ} \frac{\partial θ}{\partial σ_{i j}}) + (\frac{\partial f}{\partial η_{f}} \frac{\partial η_{f}}{\partial σ_{i j}})$ ,

(21)

式中,

$\begin{matrix} \frac{\partial I_{1}}{\partial σ_{i j}} = δ_{i j},_{}^{} {_{}^{}}_{}^{} \frac{\partial J_{2}}{\partial σ_{i j}} = s_{i j}, \\ \frac{\partial θ}{\partial σ_{i j}} = \frac{\sqrt{3}}{2 \sqrt{J_{2}^{3}} \cos 3 θ} (\frac{3 J_{3}}{2 J_{2}} s_{i j} - s_{i k} s_{k j} + \frac{2}{3} J_{2} s_{i j}) \end{matrix}$ ,

(22)

$\frac{\partial η_{f}}{\partial σ_{i j}} = \frac{2 η_{0} (A_{k i} σ_{k j} σ_{p q} σ_{p q} - A_{p k} σ_{p q} σ_{k q} σ_{i j})}{{(σ_{m n} σ_{m n})}^{2}}$ ,

(23)

$\frac{\partial f}{\partial I_{1}} = \frac{1}{3} η_{f} h \sin ϕ, \frac{\partial f}{\partial J_{2}} = \frac{1}{2} α_{f} K, \frac{\partial f}{\partial θ} = α_{f} J_{2} \frac{d K}{d θ}$ ,

(24)

$\frac{\partial f}{\partial η_{f}} = h (ξ) (p \sin ϕ - c \cos ϕ)$ ,

(25)

$α_{f} = 3 K / \sqrt{3 J_{2} K^{2} + {(e_{f} c \cos ϕ)}^{2}}$ ,

(26)

$\frac{d K}{d θ} = {\begin{matrix} - \sin θ - \frac{\cos θ \sin ϕ}{\sqrt{3}} & | θ | \leq θ_{t} \\ - 3 K_{2} \cos 3 θ & | θ | > θ_{t} \end{matrix}$ 。

(27)

然后计算塑性势函数对应力张量的偏导数。由于式（20）采取了与屈服函数相一致的形式,因此塑性势函数对应力张量的一阶偏导数只需将内摩擦角 $ϕ$ 替换为膨胀角 $ψ$ ,即

$\frac{\partial g}{\partial σ_{i j}} = (\frac{\partial g}{\partial I_{1}} \frac{\partial I_{1}}{\partial σ_{i j}} + \frac{\partial g}{\partial J_{2}} \frac{\partial J_{2}}{\partial σ_{i j}} + \frac{\partial g}{\partial θ} \frac{\partial θ}{\partial σ_{i j}}) + (\frac{\partial g}{\partial η_{f}} \frac{\partial η_{f}}{\partial σ_{i j}})$ 。

(28)

式中,

$\frac{\partial g}{\partial I_{1}} = \frac{1}{3} η_{f} h \sin ψ, \frac{\partial g}{\partial J_{2}} = \frac{1}{2} α_{g} K, \frac{\partial g}{\partial θ} = α_{g} J_{2} \frac{d K}{d θ}$ ,

(29)

$\frac{\partial g}{\partial η_{f}} = h (ξ) p \sin ψ$ ,

(30)

$α_{g} = 3 K / \sqrt{3 J_{2} K^{2} + {(e_{f} c \cos ψ)}^{2}}$ 。

(31)

1.4 弹塑性刚度矩阵

根据塑性一致性条件,对于式（13）中的屈服函数,其增量形式满足：

$d f = \frac{\partial f}{\partial σ_{i j}} d σ_{i j} + \frac{\partial f}{\partial h} \frac{\partial h}{\partial ξ} d ξ = 0$ 。

(32)

此外,考虑到应力增量和应变增量满足

$d σ_{i j} = D_{i j k l}^{e} d ε_{k l}^{e} = D_{i j k l}^{e} (d ε_{k l} - d ε_{k l}^{p})$ 。

(33)

根据塑性力学,塑性应变增量可由塑性因子 $λ$ 以流动法则表示为

$d ε_{k l}^{p} = d λ \frac{\partial g}{\partial σ_{i j}}$ 。

(34)

等效塑性剪应变 ${\bar{γ}}^{p}$ 也可以流动法则表示为

$d ξ = d {\bar{γ}}^{p} = d λ \sqrt{\frac{2}{3} dev (\frac{\partial g}{\partial σ_{i j}}) dev (\frac{\partial g}{\partial σ_{i j}})}$ 。

(35)

将式（32）～（35）联立,可解得

$d λ = H^{- 1} \frac{\partial f}{\partial σ_{i j}} D_{i j k l}^{e} d ε_{k l}^{p}$ ,

(36)

$\begin{matrix} H = \frac{\partial f}{\partial σ_{i j}} D_{i j k l}^{e} \frac{\partial g}{\partial σ_{k l}} - \\ \frac{\partial f}{\partial h} \frac{\partial h}{\partial ξ} \sqrt{\frac{2}{3} dev (\frac{\partial g}{\partial σ_{i j}}) dev (\frac{\partial g}{\partial σ_{i j}})} \end{matrix}$ ,

(37)

式中,H为塑性硬化模量。

将式（36）回代入式（33）,可得应变增量与应力增量的一致性表达：

$d σ_{i j} = D_{i j k l}^{e} (d ε_{k l} - d λ \frac{\partial g}{\partial σ_{i j}}) = D_{i j k l}^{ep} d ε_{k l}$ ,

(38)

$D_{i j k l}^{ep} = D_{i j k l}^{e} - H^{- 1} D_{i j p q}^{e} \frac{\partial f}{\partial σ_{p q}} \frac{\partial g}{\partial σ_{m n}} D_{m n k l}^{e}$ ,

(39)

式中, $D_{i j k l}^{ep}$ 即为一致性弹塑性刚度矩阵。

2. 数值算例

基于建立的柱状节理岩体的各向异性弹塑性本构模型,结合FLAC^3D软件对该模型进行了二次开发,并对柱状节理相似结构材料三轴岩石力学试验成果进行了模拟。根据国际岩石力学学会（ISRM）推荐标准,圆柱样直径为50 mm,柱体高度为100 mm,网格数量10000个,底面固定,顶面控制加载速度为5×10^-7 m/s,柱体四周施加固定围压4 MPa。

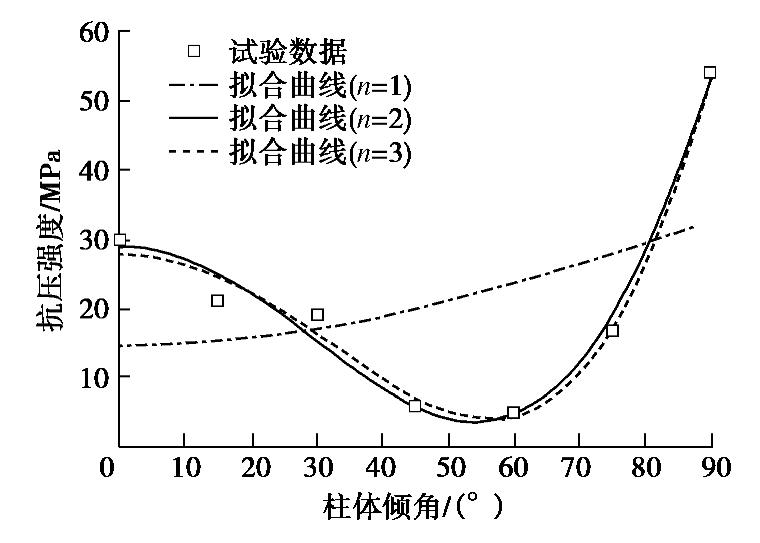
可由不同空间方向的柱状节理岩体的峰值强度进行拟合确定微结构张量系数。图2给出了强度参数关于方向角的微结构张量参数拟合曲线。

图 2 不同拟合阶数下单轴抗压强度随柱体倾角变化规律

Figure 2. Variation of uniaxial compressive strength under different fitting orders with column inclination

下载: 全尺寸图片幻灯片

为了解释固有的各向异性,假设单轴抗压强度 $f_{c}$ 受样本方向的影响,并结合与式（12）相似的分布函数来描述其变化。为了能反映材料各向异性屈服强度,并防止欠拟合和过拟合,本文采用二阶微结构张量来描述柱状节理岩体强度参数的空间分布屈服函数：

$f_{c} = \hat{f} {1 + A (1 - 3 \cos^{2} β) + b {[A (1 - 3 \cos^{2} β)]}^{2}}$ ,

(40)

式中,

$\hat{f} = 12.76 MPa, A = 1.894, b = 0.3526$ 。

(41)

其余计算参数可根据室内试验曲线^[1]数据,应用单纯形最优化方法在MATLAB中构造寻优函数编程计算得到。模型计算参数如表1所示。

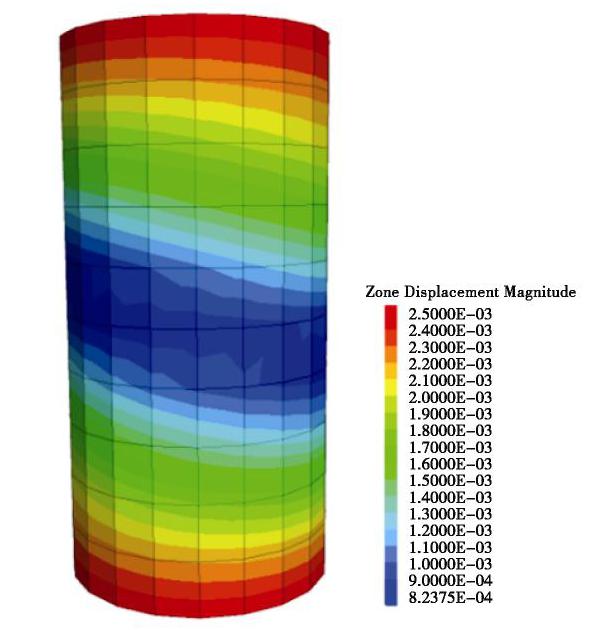
表 1 柱状节理岩体基本力学参数表

Table 1. Mechanical parameters of columnar joints

编号	^#1	^#2	^#3	^#4	^#5	^#6	^#7	^#8	^#9	^#10	^#11	^#12	^#13	^#14	^#15	^#16
参数	E₁/MPa	E₂/MPa	G₁₃/MPa	$v_{12}$	$v_{13}$	c/MPa	$φ$ /(°)	$e_{f}$	$\overset{⌢}{η}$	A	b	$h_{0}$	$h_{1}$	$e_{f}$	B	$θ_{t}$
数值	9.81	22.1	4.69	0.22	0.06	0.72	35.2	0.75	0.23	1.89	0.35	0.77	1.21	0.53	0.0018	25°

下载: 导出CSV

| 显示表格

应用表1给出的力学参数,在FLAC^3D中可以调用自定义本构模型来模拟柱状节理岩体的弹塑性变形行为。数值模拟结果如图3和图4所示。

图 3 三轴数值模拟位移云图（倾角75°,围压4 MPa）

Figure 3. Displacement nephogram by triaxial numerical simulation (angle of 75° and confining pressure of 4 MPa)

下载: 全尺寸图片幻灯片

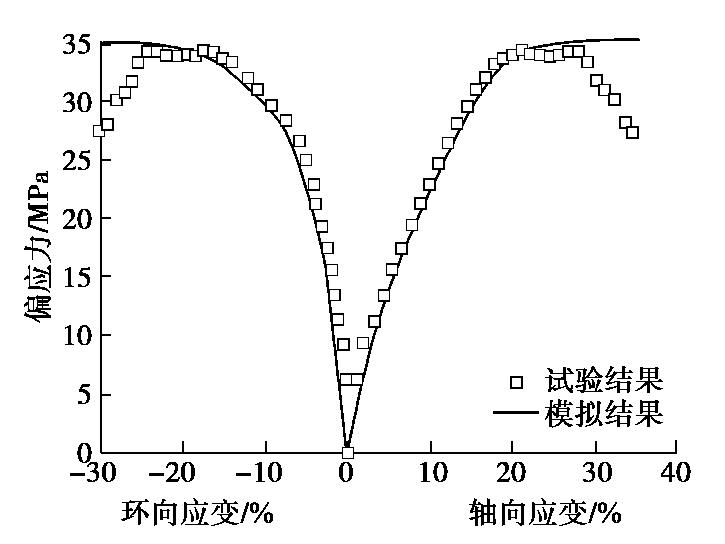
图 4 三轴试验与模拟结果对比（倾角75°,围压4 MPa）^[13]

Figure 4. Comparison between triaxial test and simulated results (angle of 75°and confining pressure of 4 MPa)

下载: 全尺寸图片幻灯片

本文将柱状节理岩体概化为横观各向同性连续体,建立描述岩体力学特性的宏观本构模型。该模型采用了一种考虑抗拉强度和屈服面角点平滑的修正Mohr–Coulomb准则,将其扩展到了空间各向异性,包含一个各向异性标量参数,该参数用应力和结构取向张量的混合不变量表示。

结果表明,柱体倾角为75°时节理岩体的变形具有明显的方向性,模拟所得应力–应变曲线与试验数据^[13]基本吻合。

应该强调的是,在对问题进行分析时,式（18）中硬化特性仅通过调用一个标量参数B来描述,由于式（18）仅限于硬化状态,不包括应变软化分支。当然也可以采用一种更复杂的方法,并假设这些特征受到围压的影响,然而这样将不可避免地生成一组额外的参数及公式。此外,该方法目的在于研究工程尺度柱状节理岩体的物理力学特性,应用了一种折中的处理策略,当研究尺度较小时,则需要进一步考虑对岩体内部的结构面开展精细模拟。

3. 白鹤滩高坝坝基开挖工程数值分析

3.1 白鹤滩坝区工程地质特征及网格建模

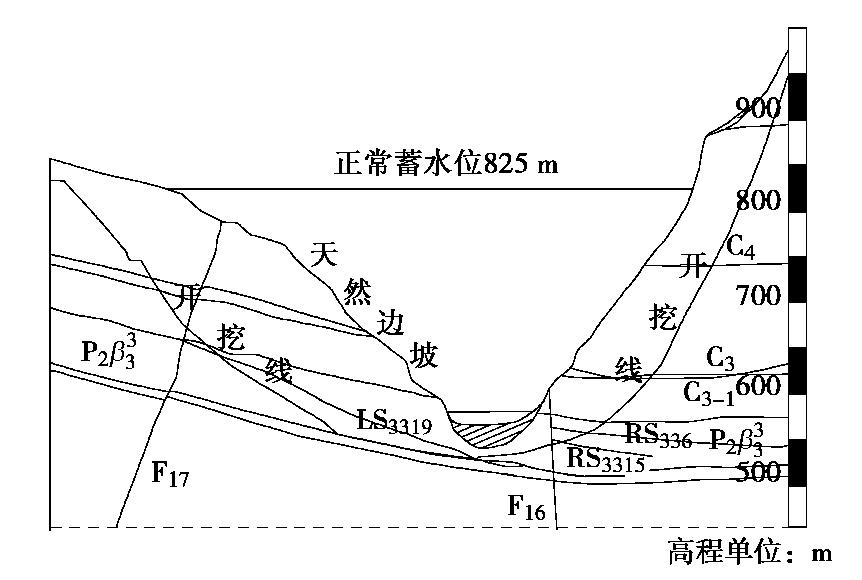
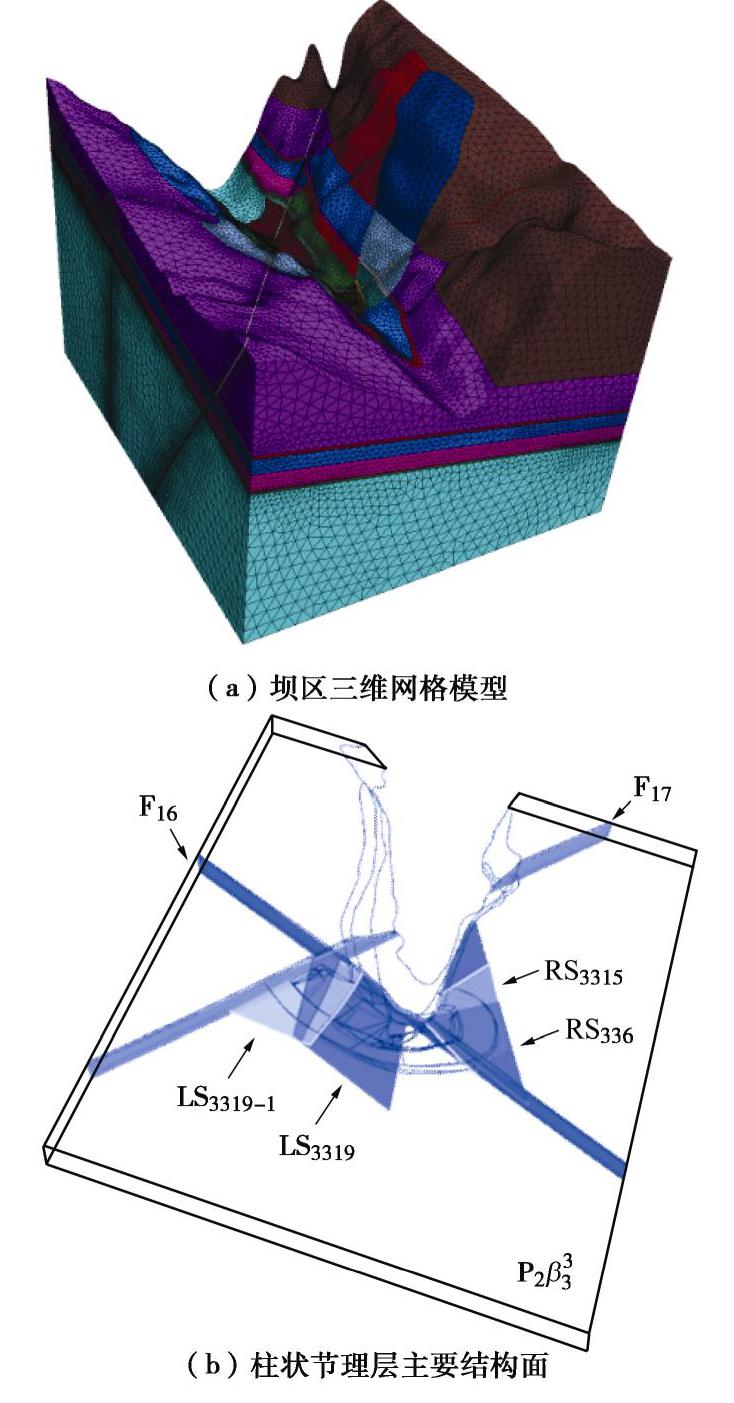
白鹤滩水电站坐落于金沙江下游云南巧家县镜内,是金沙江下游干流河段梯级开发的第二个梯级电站。主坝为混凝土双曲拱坝,最大坝高289 m,计划2022年建设完工。白鹤滩水电站坝区属中山峡谷地貌,坝址为单斜地层,主要为二叠系上统峨眉山组玄武岩,如图5,可分为11个岩流层,岩层走向N30～50°E,倾向SE,倾角15°～25°。岩层岩性主要分为斜斑玄武岩、隐晶玄武岩、柱状节理玄武岩、杏仁状玄武岩、角砾熔岩和凝灰岩等。右岸坡顶顶部出露三叠系下统飞仙关组泥质粉砂岩、粉砂质泥岩及少量砂岩^[2]。其中出露 $P_{2} β_{3}$ 层为柱状节理玄武岩,柱体长度为2～3 m,柱体倾角70°～85°,柱体截面主要为不规则五边形和四边形,截面边长为10～20 cm。柱体内部隐节理发育,开挖前节理闭合紧密^[14]。

图 5 拱坝轴线地质剖面示意图

Figure 5. Illustration of engineering geological section of arch axis

下载: 全尺寸图片幻灯片

图6（a）为开挖模拟所用网格模型,坐标原点位于拱坝轴线,建模范围为1300 m×1500 m×1296 m。在模型局部区域,对单元进行了细化剖分,网格平均边长约为1.5 m。采用Hypermesh剖分三维实体,并形成网格文件,然后将数据转换为相应的软件格式,建立了数值计算网格模型,单元总数145万个,节点26万个。坝基开挖边坡及柱状节理玄武岩体为计算分析重点关注的部位。除了层间错动带,该网格模型还考虑了断层F16、F17,以及柱状节理玄武岩层 $P_{2} β_{3}$ 中的层内错动带LS3319、LS3319-1、RS3315和RS336,如图6（b）所示。

图 6 白鹤滩坝基开挖计算网格模型

Figure 6. Calculation grid model for excavation of foundation of …Baihetan Dam

下载: 全尺寸图片幻灯片

3.2 模型参数及工况设置

对模型前后左右4个侧面施加法向约束,对底面施加x,y,z三向约束作为边界条件。模型自下而上共划分有8个地层,模型计算参数根据工程地质条件和岩石力学参数试验等确定,主要岩体力学参数如表2所示。

表 2 主要岩体基本物理力学参数

Table 2. Basic mechanical parameters of main rock mass

岩层分类	$ρ$ /(kg·m^-3)	E/GPa	$ν$	c/MPa	$φ$ /(°)
C₄层面以上	2700	11.0	0.23	1.10	47.7
C₄~C₃层面	2700	13.2	0.23	1.37	51.8
C_3-1~柱状节理顶面	2600	10.2	0.24	1.07	48.0
柱状节理层	2700	10.0	0.25	0.90	47.7
角砾熔岩层	2600	9.0	0.24	1.08	47.2
微新岩岩层	2850	22.0	0.22	2.10	57.2
C₄	2130	0.4	0.35	0.10	28.0
C₃	2130	0.4	0.34	0.10	28.0
C_3-1	2050	0.7	0.35	0.04	28.0
F₁₆	2130	1.5	0.35	0.20	29.2
F₁₇风化上段	2000	0.7	0.35	0.04	15.6
F₁₇风化下段	2130	1.2	0.35	0.05	20.8
F₁₇微新岩体	2130	2.0	0.35	0.20	29.2
LS₃₃₁	2150	1.5	0.35	0.30	30.0
LS₃₃₁₉	2110	0.3	0.35	0.10	26.0
LS_3319-1	2000	0.3	0.35	0.15	27.0
RS₃₃₆	2000	0.3	0.35	0.15	27.0
RS₃₃₁₅	2000	0.3	0.35	0.15	26.0

下载: 导出CSV

| 显示表格

考虑左右岸坝基岩石工程现场实际施工工序,依照表3对边坡开挖过程设置了10个开挖步。

表 3 模型开挖工况设置

Table 3. Setting of model excavation conditions

开挖步编号	开挖台阶高程	现场开挖完成时间
^#1	左岸800 m	2013.10.24
^#2	左岸700 m	2014.08.19
^#3	右岸800 m	2014.11.10
^#4	左岸650 m	2014.12.03
^#5	右岸700 m	2015.03.30
^#6	右岸650 m	2015.06.24
^#7	右岸600 m	2016.01.27
^#8	左岸600 m	2016.06.03
^#9	600 m高程以下	2016.07.26
^#10	保护层	2016.08.14

下载: 导出CSV

| 显示表格

3.3 计算结果分析

图7为白鹤滩开挖模型左岸坝基不同高程处测点位移变化曲线图。左岸坝基建基面岩体位移随开挖进程逐渐增大；开挖完成时,岩体位移随岩体所在高程减小而先增大后减小,坝基底部柱状节理岩体位移大于上部非柱状节理岩体。

图 7 左岸坝基不同高程处测点位移变化曲线图

Figure 7. Curves of displacement change at measurement points at different elevations of dam foundation at left bank

下载: 全尺寸图片幻灯片

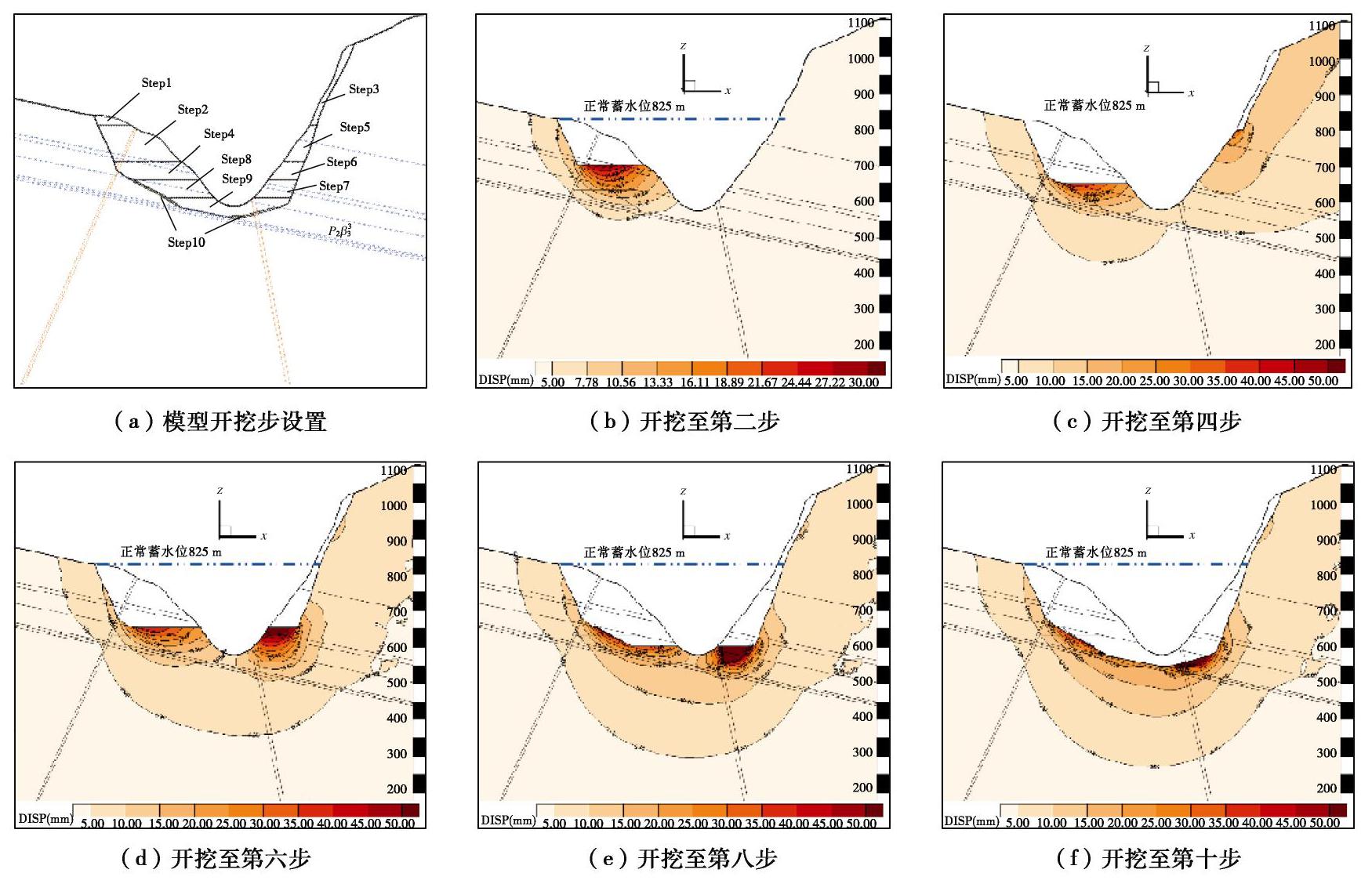
图8为考虑柱状节理岩体各向异性时白鹤滩坝基边坡开挖过程位移变化云图。

图 8 考虑柱状节理岩体各向异性模型开挖过程位移变化云图

Figure 8. Cloud charts of displacement change in excavation process considering anisotropic model of columnar jointed rock mass

下载: 全尺寸图片幻灯片

开挖完成时,建基面最大位移超过50 mm,平均位移为25～40 mm；坝基开挖全过程中,最大位移出现在各开挖步开挖梯段的边坡坡脚及开挖台阶面上；岩体变形范围和变形程度随开挖进程逐渐增大；表层岩体的变形较大,变形程度随岩体深度增加而逐渐减小；岩体变形围绕断层和错动带发展,断层和错动带周围的岩体变形显著大于不含断层和错动带的岩体（实际现场开挖中对坝基出露断层采取了置换处理）。

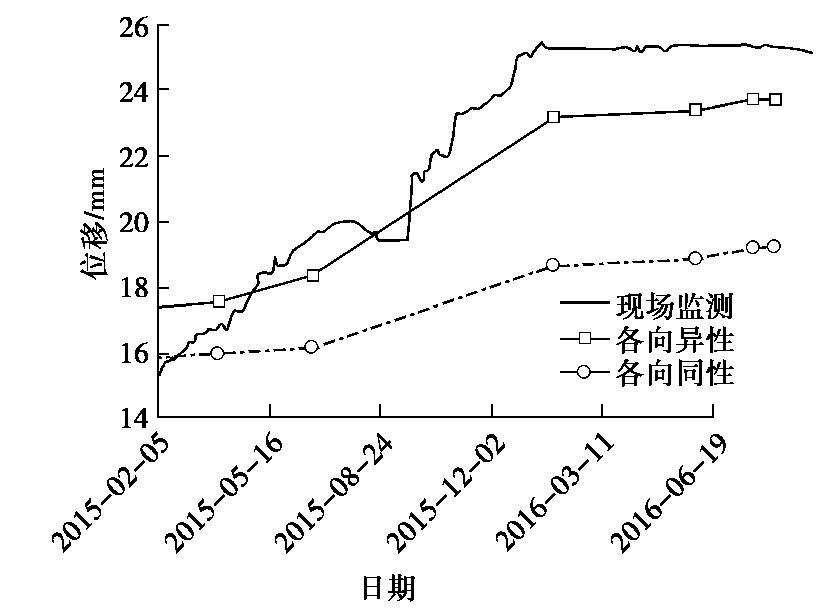
图9为左岸坝基658 m高程处多点变位计Mzjc-2监测所得位移时程曲线,以及分别采用各向异性模型和各向同性模型计算所得的变形曲线。从图中可以看到,相比于只采用各向同性模型,采用各向异性模型的位移计算结果与现场监测结果更为接近。

图 9 左岸坝基多点变位计Mzjc-2监测结果与计算结果对比

Figure 9. Comparison between monitoring and calculated results of Mzjc-2 multi-point displacement meter

下载: 全尺寸图片幻灯片

表4为坝基开挖完成时刻左岸坝基柱状节理试验区及左岸坝肩下游边坡处多点变位计变形监测结果与数值模型计算结果的对比。

表 4 坝基开挖结束时监测变形与计算位移对比

Table 4. Comparison of monitored deformations and calculated displacements at completion end of excavation of dam foundation

测点编号	监测结果/mm	各向异性模型		各向同性模型
测点编号	监测结果/mm	计算值/mm	误差/%	计算值/mm	误差/%
Mzjc-2	25.4	23.7	6.7	19.2	24.4
Mzjc-3	24.9	21.8	12.4	18.0	27.7
M_ZBJ-3	6.6	5.6	15.2	4.9	25.8

下载: 导出CSV

| 显示表格

结果表明：各向异性模型位移计算误差明显小于各向同性模型,这在柱状节理区域表现更为显著。

为生成质量较高的三维网格模型,本文所用开挖模型中开挖梯段高差（50～100 m）与实际工程施工台阶（5～10 m）存在较大差距,这在模拟计算结果中主要体现在变形的时间节点与实际监测结果存在一定出入。另一方面,本文计算所采用的各向异性弹塑性本构模型不能完整体现节理岩体卸荷松弛的时效性。在后续的工作中,考虑引入各向异性时效损伤以本文的相关工作进一步深化完善。

4. 结论

（1）结合微结构张量理论扩展了经典莫尔库仑模型,完整推导了柱状节理岩体的各向异性弹塑性本构模型。考虑各向异性的本构模型可以直观反映岩体强度的各向异性空间分布,计算所需参数均可由试验结果计算得到。

（2）结合FLAC^3D二次开发接口对自定义本构模型进行了开发。对所开发模型进行了数值验证,数值计算结果与柱状节理相似材料室内三轴压缩试验结果基本一致,表明该模型可以体现柱状节理材料的空间各向异性特性。

（3）应用所开发本构模型对白鹤滩水电站坝基边坡开挖过程进行了模拟。计算结果表明,与未考虑各向异性相比,考虑柱状节理岩体强度各向异性时坝基边坡位移更接近于现场多点位移计监测结果,本文研究工作对白鹤滩水电工程建设有一定参考价值。

图 1 全局坐标系中的柱状节理材料

Figure 1. Cylindrical joint materials in global coordinate system

下载: 全尺寸图片幻灯片

图 2 不同拟合阶数下单轴抗压强度随柱体倾角变化规律

Figure 2. Variation of uniaxial compressive strength under different fitting orders with column inclination

下载: 全尺寸图片幻灯片

图 3 三轴数值模拟位移云图（倾角75°,围压4 MPa）

Figure 3. Displacement nephogram by triaxial numerical simulation (angle of 75° and confining pressure of 4 MPa)

下载: 全尺寸图片幻灯片

图 4 三轴试验与模拟结果对比（倾角75°,围压4 MPa）^[13]

Figure 4. Comparison between triaxial test and simulated results (angle of 75°and confining pressure of 4 MPa)

下载: 全尺寸图片幻灯片

图 5 拱坝轴线地质剖面示意图

Figure 5. Illustration of engineering geological section of arch axis

下载: 全尺寸图片幻灯片

图 6 白鹤滩坝基开挖计算网格模型

Figure 6. Calculation grid model for excavation of foundation of …Baihetan Dam

下载: 全尺寸图片幻灯片

图 7 左岸坝基不同高程处测点位移变化曲线图

Figure 7. Curves of displacement change at measurement points at different elevations of dam foundation at left bank

下载: 全尺寸图片幻灯片

图 8 考虑柱状节理岩体各向异性模型开挖过程位移变化云图

Figure 8. Cloud charts of displacement change in excavation process considering anisotropic model of columnar jointed rock mass

下载: 全尺寸图片幻灯片

图 9 左岸坝基多点变位计Mzjc-2监测结果与计算结果对比

Figure 9. Comparison between monitoring and calculated results of Mzjc-2 multi-point displacement meter

下载: 全尺寸图片幻灯片

表 1 柱状节理岩体基本力学参数表

Table 1 Mechanical parameters of columnar joints

编号	^#1	^#2	^#3	^#4	^#5	^#6	^#7	^#8	^#9	^#10	^#11	^#12	^#13	^#14	^#15	^#16
参数	E₁/MPa	E₂/MPa	G₁₃/MPa	$v_{12}$ $v_{12}$	$v_{13}$ $v_{13}$	c/MPa	$φ$ $φ$ /(°)	$e_{f}$ $e_{f}$	$\overset{⌢}{η}$ $\overset{⌢}{η}$	A	b	$h_{0}$ $h_{0}$	$h_{1}$ $h_{1}$	$e_{f}$ $e_{f}$	B	$θ_{t}$ $θ_{t}$
数值	9.81	22.1	4.69	0.22	0.06	0.72	35.2	0.75	0.23	1.89	0.35	0.77	1.21	0.53	0.0018	25°

下载: 导出CSV

表 2 主要岩体基本物理力学参数

Table 2 Basic mechanical parameters of main rock mass

岩层分类	$ρ$ $ρ$ /(kg·m^-3)	E/GPa	$ν$ $ν$	c/MPa	$φ$ $φ$ /(°)
C₄层面以上	2700	11.0	0.23	1.10	47.7
C₄~C₃层面	2700	13.2	0.23	1.37	51.8
C_3-1~柱状节理顶面	2600	10.2	0.24	1.07	48.0
柱状节理层	2700	10.0	0.25	0.90	47.7
角砾熔岩层	2600	9.0	0.24	1.08	47.2
微新岩岩层	2850	22.0	0.22	2.10	57.2
C₄	2130	0.4	0.35	0.10	28.0
C₃	2130	0.4	0.34	0.10	28.0
C_3-1	2050	0.7	0.35	0.04	28.0
F₁₆	2130	1.5	0.35	0.20	29.2
F₁₇风化上段	2000	0.7	0.35	0.04	15.6
F₁₇风化下段	2130	1.2	0.35	0.05	20.8
F₁₇微新岩体	2130	2.0	0.35	0.20	29.2
LS₃₃₁	2150	1.5	0.35	0.30	30.0
LS₃₃₁₉	2110	0.3	0.35	0.10	26.0
LS_3319-1	2000	0.3	0.35	0.15	27.0
RS₃₃₆	2000	0.3	0.35	0.15	27.0
RS₃₃₁₅	2000	0.3	0.35	0.15	26.0

下载: 导出CSV

表 3 模型开挖工况设置

Table 3 Setting of model excavation conditions

开挖步编号	开挖台阶高程	现场开挖完成时间
^#1	左岸800 m	2013.10.24
^#2	左岸700 m	2014.08.19
^#3	右岸800 m	2014.11.10
^#4	左岸650 m	2014.12.03
^#5	右岸700 m	2015.03.30
^#6	右岸650 m	2015.06.24
^#7	右岸600 m	2016.01.27
^#8	左岸600 m	2016.06.03
^#9	600 m高程以下	2016.07.26
^#10	保护层	2016.08.14

下载: 导出CSV

表 4 坝基开挖结束时监测变形与计算位移对比

Table 4 Comparison of monitored deformations and calculated displacements at completion end of excavation of dam foundation

测点编号	监测结果/mm	各向异性模型		各向同性模型
测点编号	监测结果/mm	计算值/mm	误差/%	计算值/mm	误差/%
Mzjc-2	25.4	23.7	6.7	19.2	24.4
Mzjc-3	24.9	21.8	12.4	18.0	27.7
M_ZBJ-3	6.6	5.6	15.2	4.9	25.8

下载: 导出CSV

参考文献(14)

[1]	孟国涛. 柱状节理岩体各向异性力学分析及其工程应用[D]. 南京: 河海大学, 2007. MENG Guo-tao. Anisotropic Mechanical Analysis of Columnar Jointed Rock Mass and Its Engineering Application[D]. Nanjing: Hohai University, 2007. (in Chinese)
[2]	石安池, 唐鸣发, 周其健. 金沙江白鹤滩水电站柱状节理玄武岩岩体变形特性研究[J]. 岩石力学与工程学报, 2008, 27(10): 2079-2086. doi: 10.3321/j.issn:1000-6915.2008.10.016 SHI An-chi, TANG Ming-fa, ZHOU Qi-jian. Research of deformation characteristics of columnar jointed basalt at Baihetan hydropower station on Jinsha River[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 2079-2086. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.10.016
[3]	刘海宁, 王俊梅, 王思敬. 白鹤滩柱状节理岩体真三轴模型试验研究[J]. 岩土力学, 2010, 31(增刊1): 163-171. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S1028.htm LIU Hai-ning, WANG Jun-mei, WANG Si-jing. Experimental research of columnar jointed basalt with true triaxial apparatus at Baihetan Hydropower Station[J]. Rock and Soil Mechanics, 2010, 31(S1): 163-171. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S1028.htm
[4]	肖维民, 邓荣贵, 付小敏, 等. 单轴压缩条件下柱状节理岩体变形和强度各向异性模型试验研究[J]. 岩石力学与工程学报, 2014, 33(5): 957-963. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201405011.htm XIAO Wei-min, DENG Rong-gui, FU Xiao-min, et al. Model experiments on deformation and strength anisotropy of columnar jointed rock masses under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 957-963. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201405011.htm
[5]	JI H, ZHANG J C, WANG R B, et al. Experimental investigation of the anisotropic mechanical properties of a columnar jointed rock mass: Observations from laboratory-based physical modelling[J]. Rock Mechanics and Rock Engineering, 2017, 50(7): 1919-1931. doi: 10.1007/s00603-017-1192-4
[6]	KANATANI K. Characterization of structural anisotropy by fabric tensors and their statistical test[J]. Soils and Foundations, 1983, 23(4): 171-177. doi: 10.3208/sandf1972.23.4_171
[7]	KANATANI K. Distribution of directional data and fabric tensors[J]. International Journal of Engineering Science, 1984, 22(2): 149-164. doi: 10.1016/0020-7225(84)90090-9
[8]	PIETRUSZCZAK S. Formulation of anisotropic failure criteria incorporating a microstructure tensor[J]. Computers and Geotechnics, 2000, 26(2): 105-112. doi: 10.1016/S0266-352X(99)00034-8
[9]	GAO Z W, ZHAO J D, YAO Y P. A generalized anisotropic failure criterion for geomaterials[J]. International Journal of Solids and Structures, 2010, 47(22/23): 3166-3185.
[10]	钟世英, 徐卫亚. 基于微结构张量理论的柱状节理岩体各向异性强度分析[J]. 岩土力学, 2011, 32(10): 3081-3084. doi: 10.3969/j.issn.1000-7598.2011.10.032 ZHONG Shi-ying, XU Wei-ya. Anisotropic failure criterion incorporating microstructure tensor for rock mass with columnar joints[J]. Rock and Soil Mechanics, 2011, 32(10): 3081-3084. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.10.032
[11]	贾善坡, 陈卫忠, 杨建平, 等. 基于修正Mohr-Coulomb准则的弹塑性本构模型及其数值实施[J]. 岩土力学, 2010, 31(7): 2051-2058. doi: 10.3969/j.issn.1000-7598.2010.07.007 JIA Shan-po, CHEN Wei-zhong, YANG Jian-ping, et al. An elastoplastic constitutive model based on modified Mohr-Coulomb criterion and its numerical implementation[J]. Rock and Soil Mechanics, 2010, 31(7): 2051-2058. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.07.007
[12]	ZHANG J C, XU W Y, WANG H L, et al. A coupled elastoplastic damage model for brittle rocks and its application in modelling underground excavation[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 84: 130-141. doi: 10.1016/j.ijrmms.2015.11.011
[13]	LIN Z N, XU W Y, WANG H L, et al. Anisotropic characteristic of irregular columnar-jointed rock mass based on physical model test[J]. Journal of Civil Engineering, KSCE, 2016, 21(5): 1728-1734.
[14]	裴书锋, 冯夏庭, 张健聪, 等. 高边坡坝基柱状节理玄武岩开挖卸荷时效松弛特性[J]. 岩土力学, 2018, 39(10): 3743-3754. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810032.htm PEI Shu-feng, FENG Xia-ting, ZHANG Jian-cong, et al. Time-dependent relaxation characteristics of columnar jointed basalts in high-slope dam foundation during excavation[J]. Rock and Soil Mechanics, 2018, 39(10): 3743-3754. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810032.htm