大直径GFRP抗浮锚杆蠕变试验及蠕变模型

白晓宇; 郑晨; 张明义; 王永洪; 王海刚

doi:10.11779/CJGE202007014

大直径GFRP抗浮锚杆蠕变试验及蠕变模型 English Version

白晓宇^{1, 2,},
郑晨¹,
张明义^{1, 2},
王永洪^{1, 2, ,},
王海刚¹

1.
青岛理工大学土木工程学院,山东　青岛　266033
2.
山东省高等学校蓝色经济区工程建设与安全协同创新中心,山东　青岛　266033

基金项目:

国家自然科学基金项目 51708316

中国博士后科学基金项目 2018M632641

山东省博士后创新项目 201903043

详细信息

作者简介:
白晓宇(1984—),博士（后）,副教授,主要从事地基基础与城市地下工程领域的研究工作。E-mail：baixiaoyu538@163.com

通讯作者:
王永洪, E-mail：hong7986@163.com

中图分类号: TU473
计量
- 文章访问数: 323
- HTML全文浏览量: 22
- PDF下载量: 213
出版历程
- 收稿日期: 2019-10-27
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-06-30

Creep tests and standard linear solid model for large-diameter glass fiber-reinforced polymer anti-floating anchors

BAI Xiao-yu^{1, 2,},
ZHENG Chen¹,
ZHANG Ming-yi^{1, 2},
WANG Yong-hong^{1, 2, ,},
WANG Hai-gang¹

1.
School of Civil Engineering, Qingdao Technological University, Qingdao 266033, China
2.
Cooperative Innovation Center of Engineering Construction and Safety in Shandong Blue Economic Zone, Qingdao 266033, China

摘要

摘要: 为深入探究在长期应力作用下大直径GFRP抗浮锚杆的力学性能变化,通过施加长期荷载对GFRP抗浮锚杆进行了室内足尺试验。试验结果表明：试验锚杆在其破坏荷载的38%～45%荷载作用下才发生蠕变。通过标准线性固体模型对GFRP抗浮锚杆的蠕变规律进行分析,对刚度随时间变化曲线进行拟合,拟合曲线与实测曲线吻合度较好；进一步结合损伤力学理论和蠕变模型推导了GFRP抗浮锚杆的抗拔承载力,实现了GFRP抗浮锚杆长期承载力的精准预测,为GFRP锚杆在抗浮工程中的应用提供理论依据。
- GFRP抗浮锚杆 /
- 蠕变试验 /
- 长期应力 /
- 标准线性固体模型 /
- 刚度 /
- 时间损伤
Abstract: With the advancement of science and technology and the concept of green environmental protection, China's construction industry is gradually moving towards green and sustainable buildings. The application of glass fiber-reinforced polymer (GFRP) anchor rods instead of the traditional steel anchor rods and underground anti-floating engineering can not only save the engineering cost effectively, but also extend the service life of anti-floating structures and prevent the pollution of corrosion steel bars to underground environment. In order to further explore the changes of mechanical properties of large-diameter GFRP anti-floating bolts under long-term stress, an indoor full-scale test on GFRP anti-floating bolts is conducted by applying long-term loads. The test results show that the test bolt does not creep until 38%~45% of its failure load is applied. Through the standard linear solid model, the creep law of GFRP anti-floating bolts is investigated. The model fits the stiffness versus time curve, and the fitted curve agrees well with the measured one. Furthermore, the combination of damage mechanics theory and creep model is used to derive the uplift capacity of GFRP anti-floating anchors, and the accurate prediction of long-term bearing capacity of GFRP anti-floating anchors is realized, which provides a theoretical basis for the application of GFRP anchors in anti-floating engineering.
- GFRP anti-floating anchor /
- creep test /
- long-term stress /
- standard linear solid model /
- stiffness /
- time damage

HTML全文

0. 引言

随着建筑施工技术的发展、建（构）筑物埋深的增加,建筑地下结构工程的抗浮问题日益凸显。抗浮锚杆因其施工的便捷性及优异的抗浮效果成为近年来使用最为广泛的抗浮措施,抗浮工程的特殊性决定着抗浮锚杆为一项永久性工程。但抗浮锚杆处于复杂的地下环境中,地下水、围岩土体中的矿物质、地下交通轨道间的杂散电流都会对抗浮锚杆的工程质量造成危害,严重制约着其使用期限^[1-3]。因易锈蚀而导致强度降低,素来有“定时炸弹”之称的钢筋锚杆不适宜用于地下结构抗浮的工程中,非金属聚合物锚杆则成为抗浮锚杆的“主力军”。

玻璃纤维增强型聚合物（glass fiber reinforced polymer,GFRP）因其优异的抗拉性能、耐腐蚀性能、质轻且成本低廉等特性从一众纤维增强聚合物中脱颖而出,成为目前使用广泛的非金属聚合物抗浮锚杆^[4-5]。因GFRP抗浮锚杆推广年限较短,国内外对GFRP抗浮锚杆在长期荷载作用下其承载性能,即蠕变特性的研究较为全面^[6-9]。Gonilha等^[10]进行GFRP筋与混凝土蠕变试验时提出GFRP筋锚固于混凝土中的蠕变率远低于GFRP筋自身蠕变率。Li等^[11]结合FBG传感器技术,探究了在长期应力作用下B-GFRP锚杆杆体应力的变化特征。Vilanova等^[12]对GFRP锚杆及钢筋锚杆进行了长达130 d的拉拔试验,提出在长期荷载作用下GFRP锚杆与混凝土间相对滑移量大于钢筋锚杆与混凝土间相对滑移量可能为二者间黏结化学键不同所致。白晓宇等^[13]对GFRP抗浮锚杆进行长期应力下拉拔试验后,在损伤力学基础上结合Burgers模型计算提出GFRP抗浮锚杆的长期抗拔性能较好。Rossini等^[14]探究预应力GFRP-钢绞线在长期应力作用下预应力损失情况,认为GFRP材料有效解决了钢筋预应力锚杆在长期应力作用下预应力损失率较高的问题。

目前对于大直径的GFRP抗浮锚杆在长期荷载作用下的变形性能研究较少,而且涉及的模型参数较多,在工程应用中带来了极大的不便。鉴于此,本文根据室内足尺大直径GFRP抗浮锚杆（25 mm）在长期应力作用下位移的变化对其蠕变特性进行研究,并引入标准线性固体模型对其蠕变本构方程、刚度随时间变化规律进行分析,结合损伤力学理论对大直径GFRP抗浮锚杆在实际工程中的应用提供理论依据。

1. 蠕变试验方案

1.1 蠕变试验材料

（1）GFRP抗浮锚杆

本试验使用的锚杆为南京某公司生产的型号为YFH50的一次挤压成型全螺纹GFRP抗浮锚杆。本批次锚杆直径为25 mm,锚筋中玻璃纤维与环氧树脂体积比为3∶1,锚筋密度为2.1 g/cm³。经测量试验使用批次锚杆弹性模量为51 GPa,平均极限抗拔承载力为342 kN,极限抗拉强度为675 MPa,极限抗剪强度为150 MPa。

（2）混凝土

本次试验采用C30商品混凝土垂直浇筑成1000 mm×1000 mm×1600 mm的立方体试块模拟GFRP抗浮锚杆锚固围岩层,振捣密实后带模标准养护28 d后拆模。并采用同批次混凝土浇筑2组共6个100 mm×100 mm×100 mm的立方体试块,与模拟围岩层一起养护28 d后测得其平均抗压强度为28.8 MPa。

（3）锚固砂浆

本试验使用山东“山水牌”P·O 42.5普通硅酸盐水泥,砂采用级配良好的中砂,水为自来水。拟使用强度为M30的砂浆,水泥∶砂∶水的质量比为1∶1∶0.45,浇筑6个70.7 mm×70.7 mm×70.7 mm的立方体试块,标准养护28 d后测得其平均抗压强度为35.5 MPa。

1.2 试验方案

本次试验拟对4根GFRP抗浮锚杆进行长期应力作用下的室内足尺拉拔试验,试验锚杆的具体参数如表1所示。

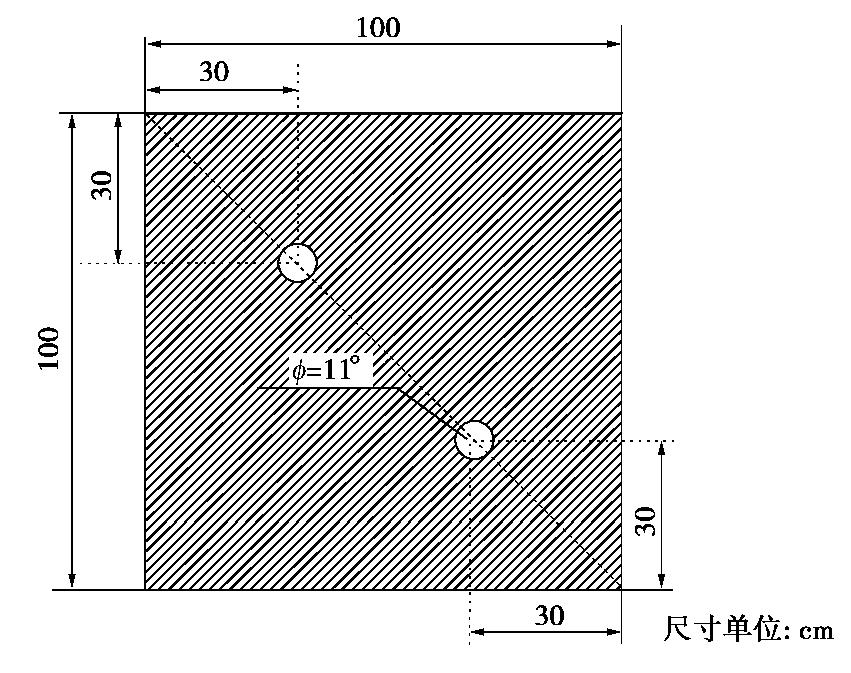
表 1 试验参数

Table 1. Test parameters

试件编号	锚杆直径/mm	锚杆长度/mm	锚固长度/mm	混凝土强度等级	砂浆强度等级
G1-G4	25	2 500	1 300	C30	M30

下载: 导出CSV

| 显示表格

将养护好的模拟围岩混凝土试块拆模后,采用潜孔钻机在试块对角线全程取芯,为防止同组两根试验锚杆上拔时互相干扰,根据以往试验经验每个孔距混凝土立方体边缘30 cm,孔位布置如图1所示。成孔完毕并清孔后将完成绑扎的试验GFRP锚杆放入孔洞中,注入配置好的M30砂浆,标准养护28 d后进行长期拉拔试验并测定其蠕变位移。

图 1 试件孔位布置示意图

Figure 1. Schematic diagram of hole position of test piece

下载: 全尺寸图片幻灯片

1.3 试验过程

（1）试验装置

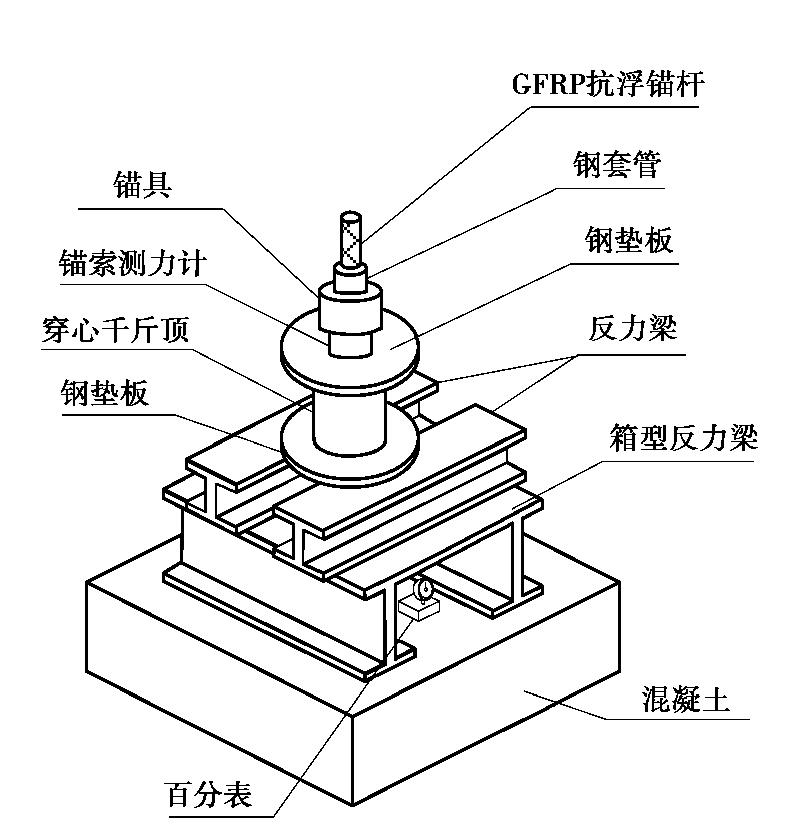
加载装置按图2布置。将试验锚杆置于中间留有孔洞,截面尺寸为700 mm×200 mm×300 mm的箱型反力梁正中央,上架设2根H型钢块。将钢垫板、1台60 t,行程为20 cm的手动式油压穿心千斤顶、山东科技大学生产的型号MGH 500锚索测力计、钢套管、锚具依次在GFRP抗浮锚杆自由段组装调试好,采用精度为0.01 mm,量程为30 mm的百分表对锚杆相对混凝土位移进行测读。

图 2 加载装置示意图

Figure 2. Schematic diagram of loading devices

下载: 全尺寸图片幻灯片

（2）加载方式

本次试验为测定GFRP抗浮锚杆在长期应力作用下的蠕变位移规律,整个加载过程采用逐级加载法,每级荷载设定为30 kN保持20 d,直至最终锚杆发生破坏。试验人员根据锚索测力计检测穿心千斤顶压力施加稳定情况,如若发生压力不足应及时补足压力,维持试验过程荷载恒定。每级荷载施加完毕后应立即测读百分表并记录位移数据,之后每隔5 min进行测读直至百分表读数恒定不再发生改变。待该级荷载稳定后,前72 h每隔4 h对百分表读数进行记录（每日0:00—8:00不进行读数）,72 h后每24 h对百分表进行测读并记录数据直至每级荷载稳定至20 d后施加下一级荷载。试验过程如图3所示。

图 3 GFRP抗浮锚杆蠕变试验过程

Figure 3. Creep test process of GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

2. 试验结果与分析

2.1 GFRP抗浮锚杆破坏形式

本次试验4根GFRP抗浮锚杆最大加载量、滑移值及破坏形态如表2所示。

表 2 蠕变试验结果统计

Table 2. Statistical results of counter-pulled tests

试件编号	锚固长度/mm	破坏荷载/kN	最终滑移量/mm	破坏形式
G1	1300	266	11.30	拔出破坏
G2	1300	231	7.65
G3	1300	227	7.20
G4	1300	220	6.98

下载: 导出CSV

| 显示表格

4根GFRP抗浮锚杆破坏形式均为外锚固段砂浆出现裂缝,锚杆与砂浆间发生黏结滑移（剪切）破坏,杆体从锚固体中拔出。因GFRP材料弹抗剪强度较小、脆性较大,对GFRP抗浮锚杆杆体施加向上的拉拔荷载时极易对锚杆杆体表面肋纹产生磨损,导致GFRP抗浮锚杆与锚固砂浆间黏结力中起主要作用的机械咬合力迅速下降,锚杆被拔出。此时GFRP抗浮锚杆杆体自身强度仍未完全发挥,锚固体系仍具有较高的抗拔力储备,这亦与白晓宇等^[13]的研究结果一致。

2.2 GFRP抗浮锚杆蠕变特性及分析

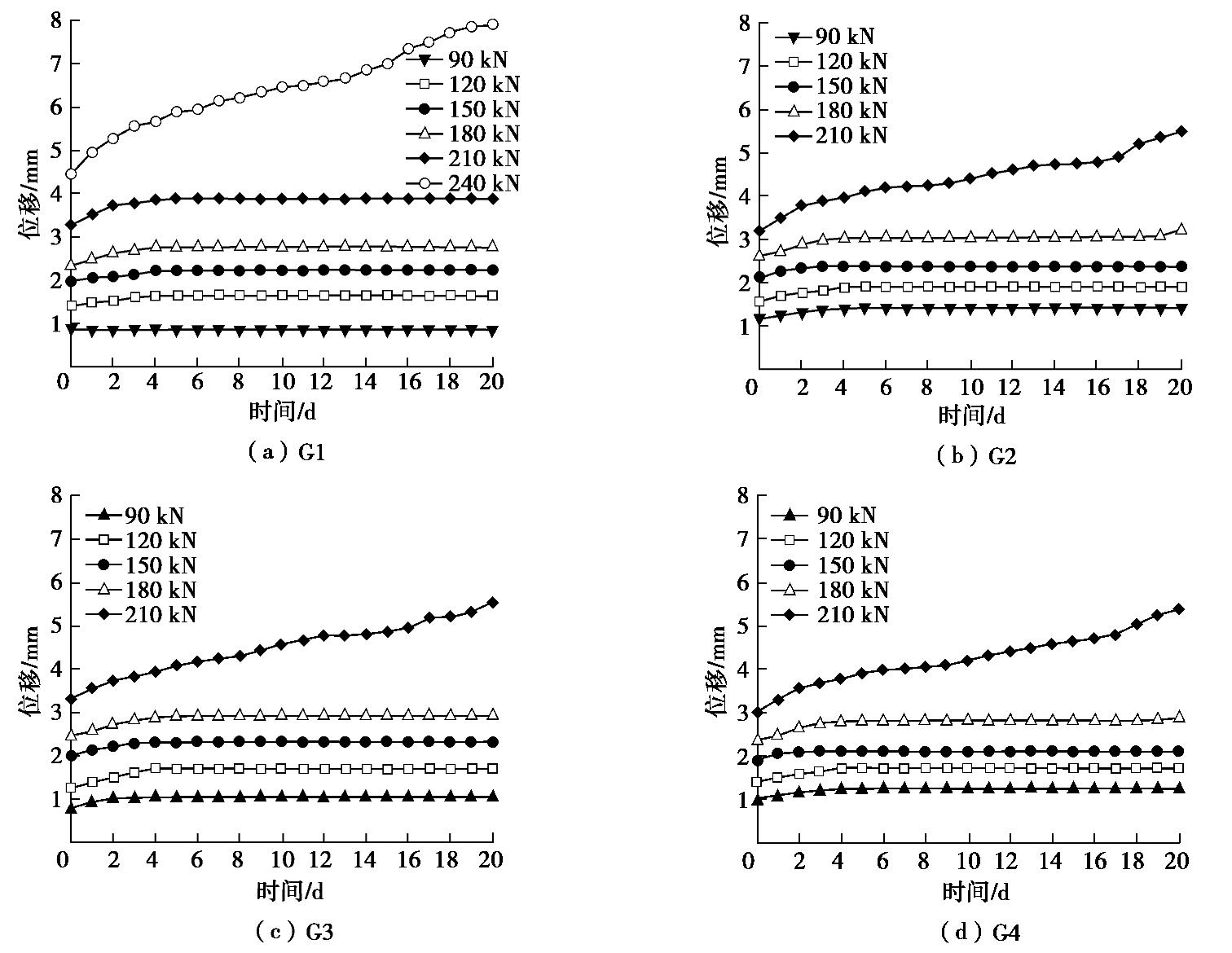
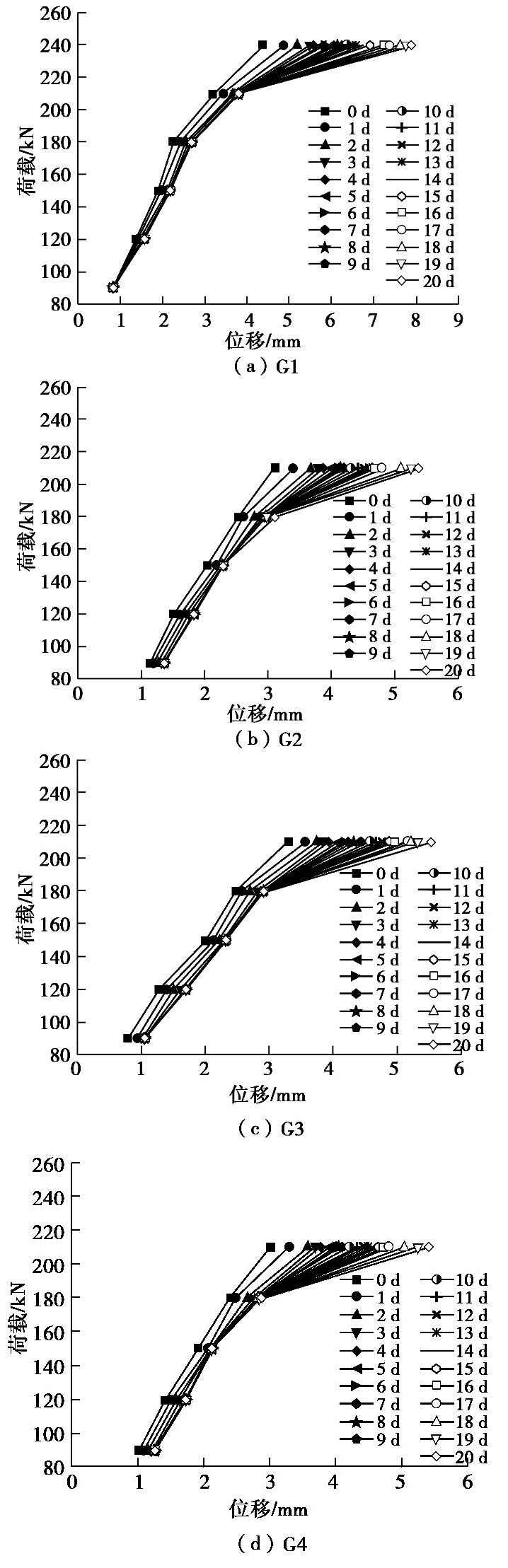
一般来说,固体材料在长期稳定的力学作用下易发生应力松弛的现象,这种在长期稳定荷载作用下产生随时间增加而增加的变形现象称之为蠕变。不同荷载水平下4根GFRP抗浮锚杆的位移–时间曲线如图4所示。

图 4 试验GFRP抗浮锚杆位移–时间曲线

Figure 4. Displacement-time curves of tested GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

由图4可知,试验锚杆G1在90 kN荷载作用下基本未发生蠕变现象,位移–时间曲线为平稳的直线；G1受到荷载为120～210 kN、G2、G3及G4受到荷载为90～180 kN每级荷载刚开始施加时,位移–时间曲线斜率出现较小增长,后续趋于平稳,为典型的衰减蠕变行为,表明此时GFRP抗浮锚杆所受荷载小于其极限抗拔荷载。当试件G1所受荷载增加至240 kN,试件G2、G3及G4所受荷载增加至210 kN时,其位移–时间曲线均呈快速上扬趋势,为非衰减蠕变,其曲线非衰减蠕变的过渡蠕变段、稳态蠕变段、加速蠕变段表现都较为明显,表明240 kN已较为接近试件G1的极限抗拔荷载,210 kN较为接近G2、G3及G4的极限抗拔荷载。且结合表2可知,试件G1产生初始蠕变荷载为120 kN,为其破坏荷载的45%；试件G2、G3及G4产生初始蠕变荷载均为90 kN,分别为其破坏荷载的38%,39%,41%,表明大直径的GFRP抗浮锚杆在其极限荷载的40%以下荷载水平工作时展现蠕变性能较优良。

3. 蠕变力学模型

3.1 标准线性固体力学模型

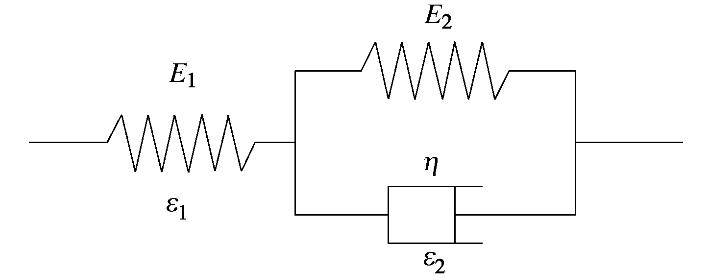
标准线性固体模型在Kelvin模型边串联了1个Hooke弹簧元件的三元件模型,用以改善原Kelvin模型未能对材料瞬时普弹性进行模拟的缺点^[15],标准线性固体模型如图5所示。

图 5 标准线性固体模型

Figure 5. Standard linear solid model

下载: 全尺寸图片幻灯片

由标准线性固体模型可得

$σ = E_{1} ε_{1}$ ,

(1)

$σ = E_{2} ε_{2} + η ε_{2}$ ,

(2)

$ε = ε_{1} + ε_{2}$ 。

(3)

式中 $σ$ 为元件所受应力；E₁,E₂为弹簧元件刚度； $ε_{1}$ , $ε_{2}$ 为元件所受应变；η为黏性元件黏度。

对式（1）～（3）进行Laplace变换后重新代入式（3）,进行逆变换可得到

（ ）

$（ E_{1} + E_{2} ） \cdot σ + η \cdot \frac{d σ}{d t} = E_{1} E_{2} ε - E_{1} η \cdot \frac{d ε}{d t}$ 。

(4)

在蠕变情况下,假设标准线性固体模型受到的恒定轴向拉力为F,则该模型蠕变方程可化为

$μ = F \cdot {\frac{1}{E_{1}} + \frac{1}{E_{2}} \cdot [1 - \exp (- \frac{E_{2}}{η} t)]}$ ,

(5)

式中,μ为模型的蠕变位移。

本文参照文献[16]设 $M = \frac{1}{E_{1}}$ , $N = \frac{1}{E_{2}}$ , $P = \frac{E_{2}}{η}$ ,并代入式（5）中可得

$μ = F \cdot [M + N \cdot (1 - e^{- P t})]$ 。

(6)

因将指数函数展开可得

$e^{x} = 1 + x + \frac{x^{2}}{2 ！} + \frac{x^{3}}{3!} + \dots \dots + \frac{x^{n}}{n!}$ ,

(7)

其展开式形式与多项式函数（ $y = a_{0} + a_{1} x + a_{2} x^{2} +$ $a_{3} x^{3} + \dots \dots + a_{n} x^{n}$ ）类似,为求解式（6）中力学参数模型,对锚杆G1及G2位移–时间曲线进行多项式线性回归分析,回归方程系数如表3～6所示。

表 3 G1回归方程系数

Table 3. Regression equation coefficient of G1

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
90	1.1962	0.06436	-0.00565	1.50860	0.93677	0.00425
120	1.5893	0.08927	-0.00778	2.06373	0.94608	0.00712
150	2.1805	0.09880	-0.00956	1.54982	0.82454	0.01124
180	2.6259	0.1270	-0.01193	3.46620	0.93477	0.01791
210	3.2676	0.2396	-0.01835	5.98803	0.98725	0.07331

下载: 导出CSV

| 显示表格

表 4 G2回归方程系数

Table 4. Regression equation coefficient of G2

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
120	1.4192	0.06208	-0.00538	1.42269	0.94623	0.00349
150	1.9697	0.06935	-0.00578	1.48587	0.95079	0.00455
180	2.3813	0.11499	-0.01032	2.79126	0.90694	0.01907
210	3.3777	0.15655	-0.01405	3.80348	0.89809	0.03902
240	4.5065	0.34547	-0.02331	7.40548	0.98811	0.18094

下载: 导出CSV

| 显示表格

表 5 G3回归方程系数

Table 5. Regression equation coefficient of G3

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
90	0.8516	0.06642	-0.0062	1.71991	0.77787	0.01501
120	1.3014	0.11761	-0.01036	2.76950	0.93243	0.01506
150	2.0481	0.12028	-0.00727	1.95009	0.91737	0.00911
180	2.4940	0.14751	-0.01055	2.78375	0.95014	0.01258
210	3.3397	0.19222	-0.01044	3.10581	0.99380	0.03882

下载: 导出CSV

| 显示表格

表 6 G4回归方程系数

Table 6. Regression equation coefficient of G4

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
90	1.0462	0.06436	-0.00565	1.50860	0.93677	0.00425
120	1.4347	0.08728	-0.00758	2.00884	0.94825	0.00658
150	1.9849	0.09635	-0.00438	1.22507	0.70148	0.01022
180	2.4220	0.17214	-0.01098	3.03600	0.93289	0.01599
210	3.0665	0.24053	-0.01846	6.00744	0.98756	0.07061

下载: 导出CSV

| 显示表格

将式（6）中 $e^{- P t}$ 展开可得

$e^{- P t} = 1 - P t + \frac{P^{2} t^{2}}{2!} - \frac{P^{3} t^{3}}{3!} + \dots \dots {(- 1)}^{n} \frac{P^{n} t^{n}}{n!},$

(8)

将式（8）代入式（6）中可得

$\begin{matrix} μ = F M + F N P t - \frac{F N P^{2} t^{2}}{2} + \\ \frac{F N P^{3} t^{3}}{6} + \dots \dots + {(- 1)}^{n - 1} \frac{F N p^{n} t^{n}}{n!} 。 \end{matrix}$

(9)

将锚杆每级得到的多项式方程 $y = a_{0} + a_{1} x + a_{2} x^{2} +$ $a_{3} x^{3} + \dots + a_{n} x^{n}$ 与式（9）联立,将每级恒定轴向拉力F代入,可解得试件G1、G2蠕变模型参数如表7～10所示。

表 7 G1力学参数表

Table 7. Mechanical parameters of G1

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
120	1.42	84.5547	2.7920	16.1082
150	1.97	76.1537	2.4036	14.4196
180	2.38	75.5890	1.5610	8.6964
210	3.38	62.1725	1.1466	6.3877
240	4.51	53.2564	0.3906	2.8946

下载: 导出CSV

| 显示表格

表 8 G2力学参数表

Table 8. Mechanical parameters of G2

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
90	1.20	75.2383	2.7280	15.5376
120	1.59	75.5049	1.9525	11.2020
150	2.18	68.7916	1.9382	10.1215
180	2.63	68.5479	1.4793	7.8740
210	3.27	64.2674	0.6393	4.1736

下载: 导出CSV

| 显示表格

表 9 G3力学参数表

Table 9. Mechanical parameters of G3

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
90	0.85	105.6834	2.8108	15.0557
120	1.30	92.2084	1.4980	8.5027
150	2.05	73.2386	1.0050	8.3139
180	2.49	72.1732	0.9697	6.7792
210	3.34	62.8799	0.5651	5.2024

下载: 导出CSV

| 显示表格

表 10 G4力学参数表

Table 10. Mechanical parameters of G4

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
90	1.05	86.0256	2.7280	15.5376
120	1.43	83.6412	1.9901	11.4574
150	1.98	75.5706	0.9436	10.3788
180	2.42	74.3187	0.7411	5.8092
210	3.07	68.4820	0.6382	4.1575

下载: 导出CSV

| 显示表格

由表7～10可以看出,4根锚杆均在轴向拉拔力最小时各模型参数达最大值,且随着作用于GFRP抗浮锚杆轴向拉拔力的增大,蠕变本构模型的参数均逐渐减小,应为微观损伤所致,这亦与许宏发等^[17]、白晓宇等^[13]的研究一致。

3.2 时效刚度

根据图4 GFRP抗浮锚杆的位移时间曲线可以得到不同时刻下不同荷载作用下的等时荷载–位移曲线,如图6所示。

图 6 GFRP抗浮锚杆荷载–位移等时曲线

Figure 6. Load-time isochronal curves of GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

等时曲线可直接观测出在不同荷载水平下同作用时间段锚杆位移变化规律。由图4可知,试件G1在不同荷载水平下荷载–位移等时曲线规律基本一致,均呈“S”型分布,表明试件在150～180 kN荷载作用下位移变化较小；试件G2及G4在每级荷载作用下第0天的荷载–位移呈近似线性关系,且试件G2、G3、G4在1 d的等时荷载–位移曲线走势十分相似,体现了GFRP抗浮锚杆与混凝土间黏结–滑移运动的趋势。自第2天起4根试验锚杆的等时曲线在较低荷载下位移增长速率均基本一致,在180,210 kN较大荷载作用下位移变化较大,表明在相同时间段内较大荷载对GFRP抗浮锚杆位移影响较大。

由等时曲线特性可知,在相同时间段不同荷载作用下其荷载–位移曲线均不是严格的线性关系,为便于后续内容分析,根据90～210 kN曲线段割线刚度进行计算。由式（6）可知在t时刻刚度与时间函数为

$K_{s} (t) = \frac{1}{M + N (1 - e^{- P t})}$ 。

(10)

对于锚杆G1及G2的割线刚度与时间曲线采用

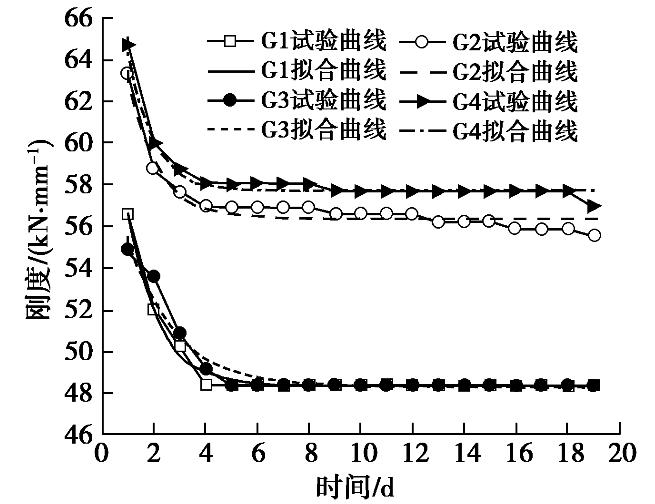
$K_{s} (t) = A \cdot \exp (- \frac{t}{b}) + B_{0}$

(11)

进行回归,第1～20天回归曲线及割线刚度与时间曲线如图7所示,函数各参数如表11所示。

图 7 GFRP抗浮锚杆荷载–位移等时曲线

Figure 7. Secant stiffness-times curve of GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

表 11 GFRP抗浮锚杆蠕变本构模型力学参数

Table 11. Creep constitutive model mechanical parameters of GFRP anti-floating anchors

试件编号	A/(mm·kN^-1)	b/(d^-1)	B₀/(mm·kN^-1)	相关系数	RSS
G1	19.2945	1.1885	48.3411	0.9904	0.0399
G2	16.7209	1.1252	56.3922	0.9393	0.1778
G3	12.2128	1.8507	48.2759	0.9538	0.1643
G4	19.7950	0.9584	57.7335	0.9773	0.0635

下载: 导出CSV

| 显示表格

联立式（10）及式（11）可解得试件G1～G4的长期割线刚度力学参数,如表12所示。

表 12 GFRP抗浮锚杆长期割线刚度力学参数

Table 12. Long-term secant stiffness mechanical parameters of GFRP anti-floating anchors

试件编号	M/(mm·kN^-1)	N/(mm·kN^-1)	P/(d^-1)	K_s/(mm·kN^-1)
G1	67.6356	-19.2945	0.8414	0.02068
G2	73.1131	-16.7209	0.8887	0.01774
G3	60.4887	-12.2128	0.5403	0.02072
G4	77.5285	-19.7950	1.0434	0.01733

下载: 导出CSV

| 显示表格

由表12可知,4根试验锚杆的长期割线抗拔刚度均较小,且波动幅度亦较小。究其原因,可能是混凝土相比于岩石层硬度低,玻璃纤维增强型材料与混凝土材料容易发生协同变形,导致锚固于混凝土底板中的GFRP抗浮锚杆长期割线刚度较小。

3.3 时间损伤效应

本次试验长期作用于GFRP抗浮锚杆的轴向拉拔力远低于其破坏荷载,此试验情况下产生的位移视为蠕变位移,损伤主要为时间损伤,变形损伤可忽略不计。根据模量法测量损伤变量,则有

$ω (t) = 1 - \frac{K_{s} (t)}{K_{s} (0)}$ 。

(12)

式中 ω(t)为GFRP抗浮锚杆在t时刻的损伤变量；K_s(t)为t时刻GFRP抗浮锚杆的刚度；K_s(0)为t＝0时GFRP抗浮锚杆的刚度,

$K_{s} (0) = \frac{1}{M}$ 。

(13)

将式（10）,（13）代入式（12）中,可得

$ω (t) = 1 - \frac{M}{M + N \cdot (1 - e^{- P t})}$ 。

(14)

当 $t \to \infty$ 即可得到GFRP抗浮锚杆的长期时间损伤变量,即

$ω (\infty) = \frac{N}{M + N}$ 。

(15)

GFRP抗浮锚杆在不同时刻下极限抗拔承载力为

$F (t) = [1 - ω (t)] \cdot F (0)$ 。

(16)

式中 F(t)为GFRP抗浮锚杆在t时刻下的极限抗拔承载力；F(0)为GFRP抗浮锚杆的极限抗拔承载力。

根据试验锚杆G1、G2、G3及G4在t＝0时的荷载与位移曲线,采用双切线法即可求得t＝0时瞬时抗拔承载力,经计算4根试件t＝0时的极限抗拔承载力近似为F(0)＝216.7 kN。

由此可得GFRP抗浮锚杆的长期抗拔承载力为

$F (\infty) = [1 - ω (\infty ）] \cdot F (0)$ ,

(17)

式中, $F (\infty)$ 为GFRP抗浮锚杆的长期抗拔承载力。

根据式（15）,（17）计算求得试验锚杆G1及G2的长期时间损伤变量及长期抗拔承载力如表13所示。

表 13 GFRP抗浮锚杆长期抗拔承载力计算值与实测值对比

Table 13. Comparison of calculated and measured values of long-term uplift capacity of GFRP anti-floating anchors

试件编号	长期时间损伤变量	$F (\infty)$ /kN	破坏荷载F_u/kN	$\frac{F (\infty)}{F_{u}}$ /%
G1	0.3991	159.84	266	60.10
G2	0.2965	162.51	231	70.35
G3	0.2529	169.59	227	74.71
G4	0.3428	144.58	220	65.72

下载: 导出CSV

| 显示表格

根据表13可看出,根据蠕变模型计算得到的GFRP抗浮锚杆的蠕变损伤变量分别为0.3991,0.2965,0.2529,0.3428,长期抗拔承载力分别为159.84,162.51,169.59,144.58 kN,约为其极限抗拔承载力的68%。究其计算长期抗拔承载力较低的原因,可能与GFRP材料特质有关。因GFRP筋的弹性模量较小,锚杆在受到轴向拉拔力后回弹性能差,在实际工程中应根据实测极限抗拔承载力值预留出40%左右的安全储备空间,防止GFRP抗浮锚杆因应力松弛而引发安全性问题。

4. 结论

（1）本文通过进行长期应力作用下的室内足尺拉拔试验探究了4根GFRP抗浮锚杆在长期应力作用下的蠕变特性,试验结果表明GFRP抗浮锚杆在其38%破坏荷载的作用下不会发生蠕变行为。

（2）引入标准线性固体模型对GFRP抗浮锚杆在长期应力作用下的蠕变规律进行探究,采用多项式回归分析的方法对试件的力学参数进行求解,参数变化证实了试验过程中发生了微观损伤。

（3）根据在同级荷载下GFRP抗浮锚杆的位移–时间等时曲线绘制其刚度–时间曲线,根据标准线性固体模型计算出4根试件刚度随时间变化公式,公式回归曲线与试验实测曲线吻合度较高,验证了模型的准确性。

（4）根据损伤力学求解GFRP抗浮锚杆的长期时间损伤变量及长期抗拔承载力,结果表明根据模型计算得到的长期抗拔承载力约为试验测得最大加载量的60%～75%,4根试验锚杆的均值为最大加载量的68%,在实际工程中应注意预留出足够的储备承载力。

图 1 试件孔位布置示意图

Figure 1. Schematic diagram of hole position of test piece

下载: 全尺寸图片幻灯片

图 2 加载装置示意图

Figure 2. Schematic diagram of loading devices

下载: 全尺寸图片幻灯片

图 3 GFRP抗浮锚杆蠕变试验过程

Figure 3. Creep test process of GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

图 4 试验GFRP抗浮锚杆位移–时间曲线

Figure 4. Displacement-time curves of tested GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

图 5 标准线性固体模型

Figure 5. Standard linear solid model

下载: 全尺寸图片幻灯片

图 6 GFRP抗浮锚杆荷载–位移等时曲线

Figure 6. Load-time isochronal curves of GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

图 7 GFRP抗浮锚杆荷载–位移等时曲线

Figure 7. Secant stiffness-times curve of GFRP anti-floating anchors

下载: 全尺寸图片幻灯片

表 1 试验参数

Table 1 Test parameters

试件编号	锚杆直径/mm	锚杆长度/mm	锚固长度/mm	混凝土强度等级	砂浆强度等级
G1-G4	25	2 500	1 300	C30	M30

下载: 导出CSV

表 2 蠕变试验结果统计

Table 2 Statistical results of counter-pulled tests

试件编号	锚固长度/mm	破坏荷载/kN	最终滑移量/mm	破坏形式
G1	1300	266	11.30	拔出破坏
G2	1300	231	7.65
G3	1300	227	7.20
G4	1300	220	6.98

下载: 导出CSV

表 3 G1回归方程系数

Table 3 Regression equation coefficient of G1

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
90	1.1962	0.06436	-0.00565	1.50860	0.93677	0.00425
120	1.5893	0.08927	-0.00778	2.06373	0.94608	0.00712
150	2.1805	0.09880	-0.00956	1.54982	0.82454	0.01124
180	2.6259	0.1270	-0.01193	3.46620	0.93477	0.01791
210	3.2676	0.2396	-0.01835	5.98803	0.98725	0.07331

下载: 导出CSV

表 4 G2回归方程系数

Table 4 Regression equation coefficient of G2

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
120	1.4192	0.06208	-0.00538	1.42269	0.94623	0.00349
150	1.9697	0.06935	-0.00578	1.48587	0.95079	0.00455
180	2.3813	0.11499	-0.01032	2.79126	0.90694	0.01907
210	3.3777	0.15655	-0.01405	3.80348	0.89809	0.03902
240	4.5065	0.34547	-0.02331	7.40548	0.98811	0.18094

下载: 导出CSV

表 5 G3回归方程系数

Table 5 Regression equation coefficient of G3

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
90	0.8516	0.06642	-0.0062	1.71991	0.77787	0.01501
120	1.3014	0.11761	-0.01036	2.76950	0.93243	0.01506
150	2.0481	0.12028	-0.00727	1.95009	0.91737	0.00911
180	2.4940	0.14751	-0.01055	2.78375	0.95014	0.01258
210	3.3397	0.19222	-0.01044	3.10581	0.99380	0.03882

下载: 导出CSV

表 6 G4回归方程系数

Table 6 Regression equation coefficient of G4

荷载/kN	a₀	a₁	a₂	a₃/10^－4	相关系数	RSS
90	1.0462	0.06436	-0.00565	1.50860	0.93677	0.00425
120	1.4347	0.08728	-0.00758	2.00884	0.94825	0.00658
150	1.9849	0.09635	-0.00438	1.22507	0.70148	0.01022
180	2.4220	0.17214	-0.01098	3.03600	0.93289	0.01599
210	3.0665	0.24053	-0.01846	6.00744	0.98756	0.07061

下载: 导出CSV

表 7 G1力学参数表

Table 7 Mechanical parameters of G1

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
120	1.42	84.5547	2.7920	16.1082
150	1.97	76.1537	2.4036	14.4196
180	2.38	75.5890	1.5610	8.6964
210	3.38	62.1725	1.1466	6.3877
240	4.51	53.2564	0.3906	2.8946

下载: 导出CSV

表 8 G2力学参数表

Table 8 Mechanical parameters of G2

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
90	1.20	75.2383	2.7280	15.5376
120	1.59	75.5049	1.9525	11.2020
150	2.18	68.7916	1.9382	10.1215
180	2.63	68.5479	1.4793	7.8740
210	3.27	64.2674	0.6393	4.1736

下载: 导出CSV

表 9 G3力学参数表

Table 9 Mechanical parameters of G3

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
90	0.85	105.6834	2.8108	15.0557
120	1.30	92.2084	1.4980	8.5027
150	2.05	73.2386	1.0050	8.3139
180	2.49	72.1732	0.9697	6.7792
210	3.34	62.8799	0.5651	5.2024

下载: 导出CSV

表 10 G4力学参数表

Table 10 Mechanical parameters of G4

荷载/kN	位移/mm	E₁/(kN·mm^-1)	E₂/(kN·mm^-1)	η/(kN·d·mm^-1)
90	1.05	86.0256	2.7280	15.5376
120	1.43	83.6412	1.9901	11.4574
150	1.98	75.5706	0.9436	10.3788
180	2.42	74.3187	0.7411	5.8092
210	3.07	68.4820	0.6382	4.1575

下载: 导出CSV

表 11 GFRP抗浮锚杆蠕变本构模型力学参数

Table 11 Creep constitutive model mechanical parameters of GFRP anti-floating anchors

试件编号	A/(mm·kN^-1)	b/(d^-1)	B₀/(mm·kN^-1)	相关系数	RSS
G1	19.2945	1.1885	48.3411	0.9904	0.0399
G2	16.7209	1.1252	56.3922	0.9393	0.1778
G3	12.2128	1.8507	48.2759	0.9538	0.1643
G4	19.7950	0.9584	57.7335	0.9773	0.0635

下载: 导出CSV

表 12 GFRP抗浮锚杆长期割线刚度力学参数

Table 12 Long-term secant stiffness mechanical parameters of GFRP anti-floating anchors

试件编号	M/(mm·kN^-1)	N/(mm·kN^-1)	P/(d^-1)	K_s/(mm·kN^-1)
G1	67.6356	-19.2945	0.8414	0.02068
G2	73.1131	-16.7209	0.8887	0.01774
G3	60.4887	-12.2128	0.5403	0.02072
G4	77.5285	-19.7950	1.0434	0.01733

下载: 导出CSV

表 13 GFRP抗浮锚杆长期抗拔承载力计算值与实测值对比

Table 13 Comparison of calculated and measured values of long-term uplift capacity of GFRP anti-floating anchors

试件编号	长期时间损伤变量	$F (\infty)$ /kN	破坏荷载F_u/kN	$\frac{F (\infty)}{F_{u}}$ /%
G1	0.3991	159.84	266	60.10
G2	0.2965	162.51	231	70.35
G3	0.2529	169.59	227	74.71
G4	0.3428	144.58	220	65.72

下载: 导出CSV

参考文献(17)

[1]	白晓宇, 张明义, 朱磊, 等. 全长黏结GFRP抗浮锚杆界面剪切特性试验研究[J]. 岩石力学与工程学报, 2018, 37(6): 1407-1418. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201806009.htm BAI Xiao-yu, ZHANG Ming-yi, ZHU Lei, et al. Experimental study on shear characteristics of interface of full-bonding glass fiber reinforced polymer anti-floating anchors[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1407-1418. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201806009.htm
[2]	YAN F, LIN Z. Bond durability assessment and long-term degradation prediction for GFRP bars to fiber-reinforced concrete under saline solutions[J]. Composite Structures, 2017, 55(11): 393-406.
[3]	白晓宇, 张明义, 王永洪, 等. GFRP抗浮锚杆与混凝土底板黏结特性现场试验[J]. 中国矿业大学学报, 2020, 49(1): 93-102. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD202001011.htm BAI Xiao-yu, ZHANG Ming-yi, WANG Yong-hong, et al. Field test on bond strength between glass fiber reinforcement polymer anti-floating anchor and concrete floor[J]. Journal of China University of Mining & Technology, 2020, 49(1): 93-102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD202001011.htm
[4]	匡政, 张明义, 白晓宇, 等. 风化岩地基GFRP抗浮锚杆力学与变形特性现场试验[J]. 岩土工程学报, 2019, 41(10): 1882-1892. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201910014.htm KUANG Zheng, ZHANG Ming-yi, BAI Xiao-yu, et al. Field tests on mechanics and deformation properties of GFRP anti-floating anchors in decomposed rock foundation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(10): 1882-1892. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201910014.htm
[5]	曾宪明, 雷志梁, 张文巾, 等. 关于锚杆“定时炸弹”问题的讨论[J]. 岩石力学与工程学报, 2001, 22(1): 143-147. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200201030.htm ZENG Xian-ming, LEI Zhi-liang, ZHANG Wen-jin, et al. Discussion on the issue of anchor "time bomb"[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 22(1): 143-147. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200201030.htm
[6]	李国维, 余亮, 吴玉财, 等. 预应力喷砂玻璃纤维聚合物锚杆的黏结损伤[J]. 岩石力学与工程学报, 2014, 33(8): 1711-1719. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201408024.htm LI Guo-wei, YU Liang, WU Yu-cai, et al. Bond damage of prestressed sand-coated glass fiber reinforced polymer anchor[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1711-1719. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201408024.htm
[7]	VILANOVA I, BAENA M, TORRES L, et al. Experimental study of bond-slip of GFRP bars in concrete under sustained loads[J]. Composites Part B: Engineering, 2015, 74: 42-52.
[8]	高丹盈, 房栋, 谷泓学. GFRP-钢绞线复合筋与混凝土黏结机理及强度计算模型[J]. 建筑结构学报, 2018, 39(4): 130-139. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201804015.htm GAO Dao-ying, FANG Dong, GU Hong-xue. Bonding mechanism and strength calculation model of GFRP-steel composite rebars embedded in concrete[J]. Journal of Building Structures, 2018, 39(4): 130-139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201804015.htm
[9]	YOO D Y, KWON K Y, PARK J J. Local bond-slip response of GFRP rebar in ultra-high-performance fiber-reinforced concrete[J]. Composite Structures, 2015, 120: 53-64.
[10]	GONILHA J A, CORREIA J R, BRANCO F A. Creep response of GFRP–concrete hybrid structures: application to a footbridge prototype[J]. Composites Part B: Engineering, 2013, 53: 193-206.
[11]	LI G W, PEI H F, HONG C Y. Study on the stress relaxation behavior of large diameter B-GFRP bars using FBG sensing technology[J]. International Journal of Distributed Sensor Networks, 2013, 9(10): 1-12.
[12]	VILANOVA I, BAENA M, TORRES L, et al. Experimental study of bond-slip of GFRP bars in concrete under sustained loads[J]. Composites Part B: Engineering, 2015, 74(1): 42-52.
[13]	白晓宇, 张明义, 张舜泉. 全长黏结螺纹玻璃纤维增强聚合物抗浮锚杆蠕变试验研究[J]. 岩石力学与工程学报, 2015, 34(4): 804-813. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201504018.htm BAI Xiao-yu, ZHANG Ming-yi, ZHANG Shun-quan. Creep testing on anti-floating anchors of full-length bonding thread glass fiber reinforced polymer(GFRP)[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(4): 804-813. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201504018.htm
[14]	ROSSINI M, NANNI A. Composite strands for prestressed concrete: state-of-the-practice and experimental investigation into mild prestressing with GFRP[J]. Construction and Building Materials, 2019, 205: 486-498.
[15]	马明. CFRP加固钢筋混凝土梁长期力学特性研究[D]. 成都: 西南交通大学, 2017. MA Ming. Study on Long-Time Behavior of RC Beams Strengthened with Externally Bonded CFRP[D]. Chengdu: Southwest Jiaotong University, 2017. (in Chinese)
[16]	许宏发, 陈新万. 多项式回归间接求解岩石流变力学参数的方法[J]. 有色金属, 1994, 46(4): 19-22. https://www.cnki.com.cn/Article/CJFDTOTAL-YOUS404.003.htm XU Hong-fa, CHEN Xin-wan. Method to find indirectly solution of rock rheology's parameters with polynomial regression[J]. China Nonferrous Metals, 1994, 46(4): 19-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YOUS404.003.htm
[17]	许宏发, 卢红标, 钱七虎. 土层灌浆锚杆的蠕变损伤特性研究[J]. 岩土工程学报, 2002, 24(1): 61-63. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200201013.htm XU Hong-fa, LU Hong-biao, QIAN Qi-hu. Creep damage effects of pulling grouting anchor in soil[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 61-63. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200201013.htm

施引文献(12)

期刊类型引用(9)

1.	辛灏辉，高卿林，冯鹏，刘玉擎. 桥梁结构中E-GFRP单向板徐变性能与双尺度均匀化数值评估. 工程力学. 2024(08): 93-106 . 百度学术
2.	熊壮，杨学祥，范济敏. 充气膨胀控制锚杆的蠕变试验. 科学技术与工程. 2024(26): 11385-11392 . 百度学术
3.	陈文杰，叶毅荣. 玻璃纤维筋抗浮锚杆在某工程中的抗拔试验研究与应用. 广东建材. 2024(10): 76-79 . 百度学术
4.	刘鹏，刘军，郑仔弟，郑辉，白雪. 基于GFRP筋与钢绞线复合式锚杆支护施工的关键技术研究. 市政技术. 2023(08): 245-252 . 百度学术
5.	井德胜，白晓宇，王海刚，张明义，李翠翠，焦玉进，闫君，王忠胜. 玻璃纤维增强聚合物锚杆蠕变性能研究进展. 复合材料科学与工程. 2022(02): 119-128 . 百度学术
6.	白晓宇，井德胜，张明义，涂兵雄，魏国，吕承禄，黄春霞. 全长黏结非金属抗浮锚杆体系设计方法研究. 中南大学学报(自然科学版). 2022(08): 3168-3177 . 百度学术
7.	井德胜，白晓宇，刘超，刘永江，张明义，黄永峰. 抗浮锚杆荷载-位移特性及极限承载力预测. 科学技术与工程. 2021(22): 9570-9576 . 百度学术
8.	井德胜，白晓宇，冯志威，张明义，李翠翠. 玄武岩纤维增强聚合物锚杆用于地下结构抗浮的可行性研究. 材料导报. 2021(19): 19223-19229 . 百度学术
9.	白晓宇，刘雪颖，张明义，井德胜，郑晨. GFRP筋及钢筋抗浮锚杆承载特性现场试验及荷载-位移模型. 复合材料学报. 2021(12): 4138-4149 . 百度学术

其他类型引用(3)

资源附件(0)

图(7) / 表(13)

计量

文章访问数: 323
HTML全文浏览量: 22
PDF下载量: 213
被引次数: 12

0. 引言
1. 蠕变试验方案
1.1 蠕变试验材料
1.2 试验方案
1.3 试验过程
2. 试验结果与分析
2.1 GFRP抗浮锚杆破坏形式
2.2 GFRP抗浮锚杆蠕变特性及分析
3. 蠕变力学模型
3.1 标准线性固体力学模型
3.2 时效刚度
3.3 时间损伤效应
4. 结论

大直径GFRP抗浮锚杆蠕变试验及蠕变模型 English Version

作者简介: 白晓宇(1984—),博士（后）,副教授,主要从事地基基础与城市地下工程领域的研究工作。E-mail：baixiaoyu538@163.com

通讯作者: 王永洪, E-mail：hong7986@163.com

计量

出版历程

Creep tests and standard linear solid model for large-diameter glass fiber-reinforced polymer anti-floating anchors

0. 引言

1. 蠕变试验方案

1.1 蠕变试验材料

1.2 试验方案

1.3 试验过程

2. 试验结果与分析

2.1 GFRP抗浮锚杆破坏形式

2.2 GFRP抗浮锚杆蠕变特性及分析

3. 蠕变力学模型

3.1 标准线性固体力学模型

3.2 时效刚度

3.3 时间损伤效应

4. 结论

期刊类型引用(9)

其他类型引用(3)

计量

出版历程

目录

0. 引言

1. 蠕变试验方案

1.1 蠕变试验材料

1.2 试验方案

1.3 试验过程

2. 试验结果与分析

2.1 GFRP抗浮锚杆破坏形式

2.2 GFRP抗浮锚杆蠕变特性及分析

3. 蠕变力学模型

3.1 标准线性固体力学模型

3.2 时效刚度

3.3 时间损伤效应

4. 结论

作者简介:
白晓宇(1984—),博士（后）,副教授,主要从事地基基础与城市地下工程领域的研究工作。E-mail：baixiaoyu538@163.com

通讯作者:
王永洪, E-mail：hong7986@163.com